Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers
Подождите немного. Документ загружается.

6.6 Examples and Applications of Fourier Series 181
We can readily find that
a
k
=0,k=0, 1, 2,....
The coefficients b
k
are given by
b
k
=
1
π
π
−π
f (x)sinkx dx
=
1
π
π
−π
x sin kx dx =
2
k
(−1)
k+1
.
Hence, the Fourier series is
f (x)=2
∞
k=1
(−1)
k+1
sin kx
k
=2
sin x
1
−
sin 2x
2
+
sin 3x
3
−
sin 4x
4
+ ...
.
(6.6.7)
This Fourier series does not agree with the function at every point in [−π, π].
At the endpoints x =+
π, the series is equal to zero, but the function does
not vanish at either endpoint. However, the Fourier series (6.6.7) converges
to the value x at each point x in −π<x<π, but it converges to 0 =
1
2
[f (π − 0) + f (π + 0)] =
1
2
(π − π) which is the mean value of the two
limits as x → +
π. Thus, the convergence is not uniform. The partial sum
of the series is
s
n
(x)=2
n
k=1
1
k
(−1)
k+1
sin kx. (6.6.8)
In the neighborhood of x =+
π, the difference between f (x)and s
n
(x)
seems not to become smaller as n increases, but the size of the region where
this o ccurs decreases indicating nonuniform convergence. This nonuni-
form oscillatory nature close to discontinuities is known as the Gibbs phe-
nomenon.
It is important to p oint out that the sawtooth wave function f is not
continuous in each point in [−π, π]. What happens in the neighborhood of
x =+
π?
We consider the partial sum s
n
(x) given by (6.6.8), an d put x
n
= π −
π
n
to approximate the value s
n
(x). We have
s
n
(x
n
)=
n
k=1
2(−1)
k+1
k
sin k
π −
π
n
=
n
k=1
2
k
sin
kπ
n
whichcanberewrittenintheform
=2
n
k=1
sin
πk
n
πk
n
·
π
n
. (6.6.9)
182 6 Fourier Series and Integrals with Applications
This sum can be identified with a Riemann sum of the definite integral
2
π
0
sin x
x
dx
which is obtained by dividing the interval [0,π] into the n subintervals
"
(k−1)π
n
,
kπ
n
#
,1≤ k ≤ n.Obviously,eachsubintervalisoflength
π
n
,and
we evaluate the function in each such subinterval at the right-hand endpoint
kπ
n
,1≤ k ≤ n. Consequently,
lim
n→∞
s
n
(x)=2
π
0
sin x
x
dx ≈ 1.18π.
The point x
n
,asn →∞, approaches x = π from the left. Hence, f (x
n
)
tends to the value π. The jump at the point x = π is f (π−) −f (π+) = 2π,
and, therefore, for sufficiently large n,
s
n
(x
n
) − f (x
n
)
f (π−) − f (π+)
≈
1.18π − π
2π
=0.09.
We next draw the graphs of s
7
(x)ands
10
(x) which exhibit oscillations over
the graph of f as shown in Figures 6.6.4 (a) and (b). These graphs show
the so-called overshooting in a neighborhood of x =+
π and x =+3π,and
hence, the Gibbs phenomenon.
We next derive the sum of several numerical series from Example 6.6.3.
Substituting x =
π
2
in (6.6.7) gives
π
2
=2
∞
k=1
(−1)
k+1
k
sin
πk
2
=2
1 −
1
3
+
1
5
−
1
7
+ ...
.
This gives the well-known slowly convergent numerical series
1 −
1
3
+
1
5
−
1
7
+ ... =
π
4
. (6.6.10)
On the other hand, putting x =
π
4
in (6.6.7) gives another numerical series
π
8
=
1
√
2
−
1
2
+
1
3
√
2
−
1
5
√
2
−
1
6
−
1
7
√
2
+
1
9
√
2
−
1
10
+
1
11
√
2
−
1
13
√
2
+
1
14
− ...
=
1
√
2
1+
1
3
−
1
5
−
1
7
+
1
9
+
1
11
− ...
−
1
2
1 −
1
3
+
1
5
−
1
7
+ ...
In view of (6.6.10), we obtain another numerical series
1+
1
3
−
1
5
−
1
7
+
1
9
+
1
11
− ... =
π
2
√
2
. (6.6.11)
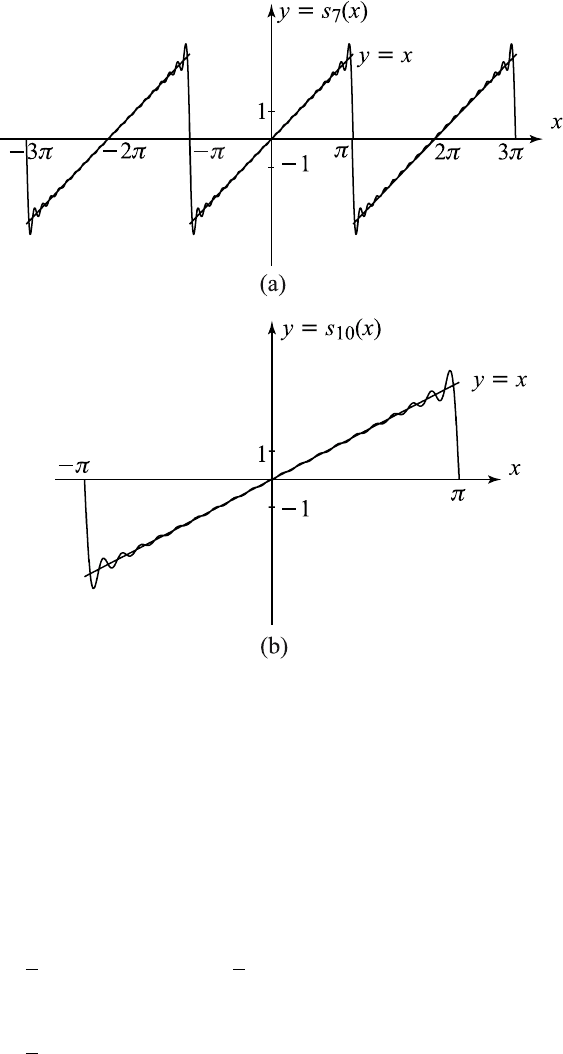
6.7 Examples and Applications of Cosine and Sine Fourier Series 183
Figure 6.6.4 Graphs of s
7
(x) in (a) and s
10
(x) in (b).
6.7 Examples and Applications of Cosine and Sine
Fourier Series
Let f (x) be an even function defined on the interval [−π,π]. Since cos kx
is an even function, and sin kx an odd function, the function f (x)coskx is
an even function and the function f (x)sinkx an odd function. Thus, we
find that the Fourier coefficients of f (x)are
a
k
=
1
π
π
−π
f (x)coskx dx =
2
π
π
0
f (x)coskx dx, k =0, 1, 2,...,
(6.7.1)
b
k
=
1
π
π
−π
f (x)sinkx dx =0,k=1, 2, 3,....

184 6 Fourier Series and Integrals with Applications
Hence, the Fourier series of an even function can be written as
f (x) ∼
a
0
2
+
∞
k=1
a
k
cos kx, (6.7.2)
where the coefficients a
k
are given by formula (6.7.1).
In a similar manner, if f (x) is an odd function, the function f (x)coskx
is an odd function and the fun ction f (x)sinkx is an even function. As a
consequence, the Fourier coefficients of f (x), in this case, are
a
k
=
1
π
π
−π
f (x)coskx dx =0,k=0, 1, 2,..., (6.7.3)
b
k
=
1
π
π
−π
f (x)sinkx dx =
2
π
π
0
f (x)sinkx dx, k =1, 2,....(6.7.4)
Therefore, the Fourier series of an odd function can be written as
f (x)=
∞
k=1
b
k
sin kx, (6.7.5)
where the coefficients b
k
are given by formula (6.7.4).
Example 6.7.1. Obtain the Fourier series of the function
f (x)=sgnx =
⎧
⎨
⎩
−1, −π<x<0,
0,x=0,
+1, 0 <x<π,
and f (x+
2kπ)=f (x) .
In this case, f is an odd function with period 2π and represents square
wave function as shown in Figure 6.7.1. Clearly, a
k
=0fork =0, 1, 2, 3,...
and
b
k
=
2
π
π
0
f (x)sinkx dx
=
2
π
π
0
sin kx dx =
2
kπ
"
1 − (−1)
k
#
.
Thus, b
2k
= 0 and b
2k−1
=[(4/π)(2k − 1)]. Therefore, the Fourier series of
the function f (x)is
f (x)=
4
π
∞
k=1
sin (2k − 1) x
(2k − 1)
. (6.7.6)
This Fourier series consists of only odd harmonics. The loss of even
harmonics is due to the fact that sgn
1
2
+ x
=sgn
1
2
− x
.
Putting x =
π
4
in (6.7.6) gives (6. 6.10).
The nth partial sum of the series (6.7.6) is

6.7 Examples and Applications of Cosine and Sine Fourier Series 185
Figure 6.7.1 The square wave function.
s
n
(x)=
4
π
n
k=1
sin (2k − 1) x
(2k − 1)
. (6.7.7)
We now examine the manner in which the first n terms of the series (6.7.7)
tend to f (x)asn →∞. The graphs of s
n
(x)forn =1, 3, 5isshownin
Figure 6.7.2. To investigate the oscillations as n →∞, we locate the first
peak to the right of the origin and calculate its height as n →∞.
Figure 6.7.2 The Gibbs phenomenon.
186 6 Fourier Series and Integrals with Applications
The peak overshoot occurs at a local maximum of the partial sum s
n
(x)
so that
0=s
′
n
(x)=
4
π
n
k=1
cos (2k − 1) x
=
2
π sin x
n
k=1
2sinx cos (2k − 1) x
=
2
π sin x
n
k=1
[sin 2kx − sin (2k − 2) x]
=
2sinnx
π sin x
. (6.7.8)
This leads to the points of maximum at x =
π
2n
,
2π
2n
,...,(2n − 1)
π
2n
so
that the first peak to the right of the origin occurs at x =
π
2n
. So, the value
of s
n
(x)atthispointis
s
n
π
2n
=
2
π
·
π
n
n
k=1
sin (2k − 1)
π
2n
(2k − 1)
π
2n
.
In the limit as n →∞, this becomes
lim
n→∞
s
n
π
2n
=
2
π
lim
n→∞
π
n
n
k=1
sin (2k − 1)
π
2n
(2k − 1)
π
2n
=
2
π
π
0
sin x
x
dx =
2
π
(1.852) = 1.179.
Instead of a maximum value 1, it turns out to be 1.179 approximately.
If the overshoot is compared to the jump in the function it is about
1
2
(1.179 − 1) × 100% ∼ 9%. The onset of the Gibbs phenomenon is shown
in the Figure 6.7.3.
Historically, this phenomenon was first observed by a physicist A.
Michelson (1852–1931) at the end of the nineteenth century. In order to
calculate some Fou rier coefficients of a function graphically, he developed
equipment that is called a harmonic analyser and synthesizer. He calcu-
lated some partial sums, s
n
, of a given function f graphically. Michelson
also observed from this graphical representation that, for some functions,
the graphs of s
n
were very close to the function. However, for the sgn
function, the graphs of the partial sums exhibit a large error in the neigh-
borhood of the origin, x = 0 and x =+
π (the jump discontinuities of
the function) independent of the number of terms in the partial sums. It
was J.W. Gibbs (1839–1903) who first provided the explanation for this
strikingly new phenomenon and showed that these large errors were not as-
sociated with nu merical computations. Indeed, he further showed that the

6.7 Examples and Applications of Cosine and Sine Fourier Series 187
Figure 6.7.3 The Gibbs phenomenon.
large errors occur at every jump discontinuity for every piecewise continu-
ous function f in [−π, π] with certain derivative properties near the jump
discontinuity.
Example 6.7.2. Expand |sin x| in Fourier series. Since |sin x| is an even func-
tion, as shown in Figure 6.7.4, b
k
=0fork =1, 2,... and
a
k
=
2
π
π
0
f (x)coskx dx
=
2
π
π
0
sin x cos kx dx
=
1
π
π
0
[sin (1 + k) x +sin(1− k) x] dx
=
2
"
1+(−1)
k
#
π (1 − k
2
)
for k =0, 2, 3,....
For k =1,
a
1
=
2
π
π
0
sin x cos xdx=0.
Hence, the Fourier series of f (x)is
f (x)=
2
π
+
4
π
∞
k=1
cos (2kx)
(1 − 4k
2
)
.
Example 6.7.3. Find the Fourier series of the triangular wave function which
is defined by
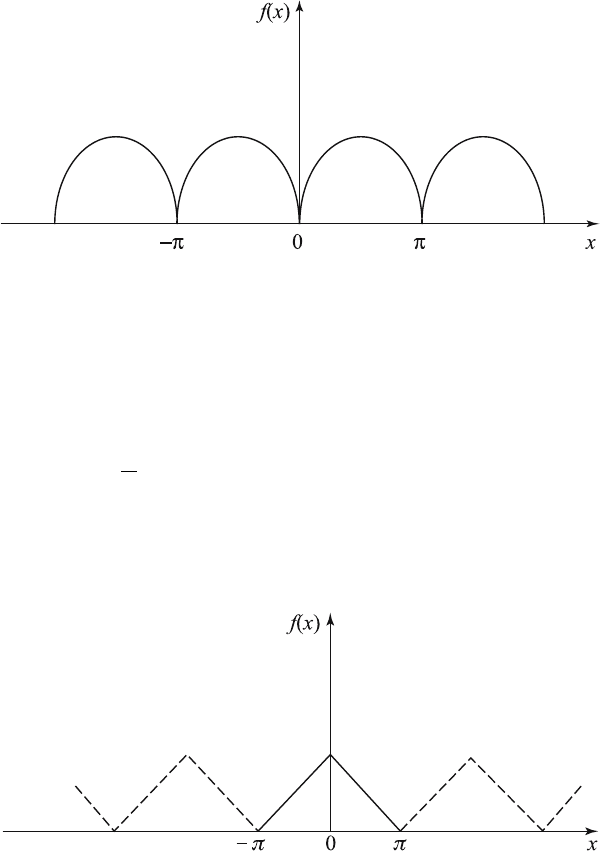
188 6 Fourier Series and Integrals with Applications
Figure 6.7.4 The rectified sine function.
f (x)=|x| =
⎧
⎨
⎩
−x, −π ≤ x ≤ 0
x, 0 ≤ x ≤ π
(6.7.9)
and f (x)=f (x +
2nπ), n =1, 2, 3,....
This is an even periodic function with period 2π as shown in Figure 6.7.5.
This function gives a Fourier cosine series with b
n
=0foralln and
Figure 6.7.5 Triangular wave function.

6.7 Examples and Applications of Cosine and Sine Fourier Series 189
a
0
=
1
π
π
−π
|x|dx =
2
π
π
0
xdx = π
a
n
=
1
π
π
−π
|x|cos nx dx =
2
π
π
0
|x|cos nx dx
=
2
π
π
0
x cos nx dx =
2
π
x sin nx
n
π
0
−
π
0
sin nx
n
dx
,
integrating by parts
=
2
πn
2
[cos nx]
π
0
=
2
πn
2
[(−1)
n
− 1] =
⎧
⎨
⎩
0, if n is even,
−
4
πn
2
if n is odd.
Thus, the Fourier cosine series is given by
f (x)=
1
2
a
0
+
∞
n=1
a
n
cos nx
=
π
2
−
4
π
cos x
1
2
+
cos 3x
3
2
+
cos 5x
5
2
+ ...
. (6.7.10)
Substituting x = 0 in (6.7.10) yields the following numerical series
π
2
8
=
1
1
2
+
1
3
2
+
1
7
2
+ ... =
∞
n=1
1
(2n − 1)
2
. (6.7.11)
This series can be used to derive the sum of reciprocals of squares of all
positive integers,
S =
∞
n=1
1
n
2
=
π
2
6
(6.7.12)
and vise versa.
We have
π
2
8
=
∞
n=1
1
(2n − 1)
2
=
∞
n=1
1
n
2
−
∞
n=1
1
(2n)
2
= S −
1
4
∞
n=1
1
n
2
= S −
1
4
S.
This gives (6.7.12).
The series (6.7.12) is just the value of s = 2 of the Riemann zeta fu nction
defined by
ζ (s)=
∞
n=1
1
n
s
, (6.7.13)
190 6 Fourier Series and Integrals with Applications
where s may be complex. This definition of ζ (s) can be extended in a nat-
ural way and this extension is called the analytic continuation of ζ (s)to
include all complex numbers s except for s = 1. This function was intro-
duced by Bernhard Riemann in 1841. He p roved many properties of this
function and made several conjectures, some of which are still open prob-
lems in mathematics. It is well known th at ζ (s) has zeros on the real axis
only at the even negative integers. Riemann conjectured that all complex
zeros of ζ (s) lie on the line Re (s)=
1
2
.ThisiscalledtheRiemann Hypoth-
esis; it is still an unsolved problem in mathematics. However, it is proved
that there are an infinite number of zeros on the line. Indeed, by the fall of
2002, fifty billion complex zeros have been found — all of them lie on the
stated line.
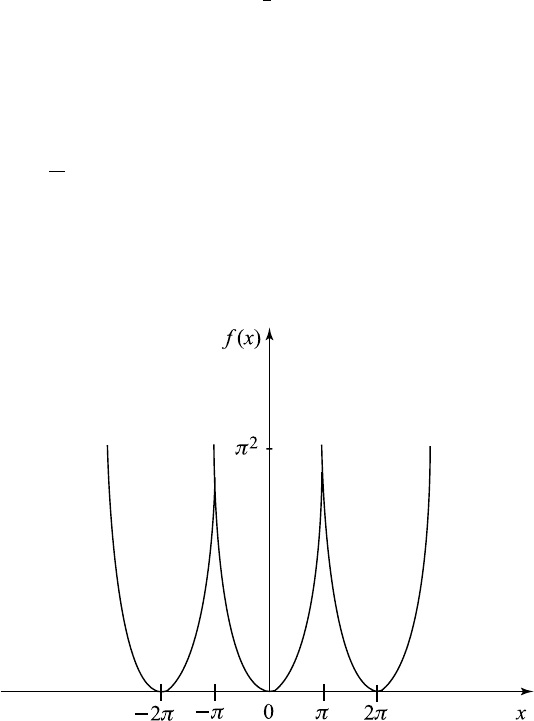
Example 6.7.4. Obtain the Fourier series of f (x)=x
2
, −π ≤ x ≤ π ,with
f (x)=f (x +
2nπ), for n =1, 2,....
Obviously, this is an even function, and its periodic extensions are shown
in Figure 6.7.6.
Since f (x) is an even function, b
n
≡ 0 for all n ≥ 1. It turns out that
Figure 6.7.6 Periodic extension of x
2
.
