Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

5.12 Exercises 161

12. Determine the solution of th e initial boundary-value problem

= c

, 0 <x<∞,t>0,

u (x , 0) = f (x) , 0 ≤ x<∞,

(x, 0) = 0, 0 ≤ x<∞,

(0,t)+hu(0,t)=0,t≥ 0,h= constant.

State the compatibility condition of f.

13. Find the solution of the problem

= c

,at<x<∞,t>0,

u (x , 0) = f (x) , 0 <x<∞,

(x, 0) = 0, 0 <x<∞,

u (a t, t)=0,t>0,

where f (0) = 0 and a is constant.

14. Find the solution of the initial boundary-value problem

= u

, 0 <x<2,t>0,

u (x , 0) = sin (πx/2) , 0 ≤ x ≤ 2,

(x, 0) = 0, 0 ≤ x ≤ 2,

u (0,t)=0,u(2,t)=0,t≥ 0.

15. Find the solution of the initial boundary-value problem

=4u

, 0 <x<1,t>0,

u (x , 0) = 0, 0 ≤ x ≤ 1,

(x, 0) = x (1 − x) , 0 ≤ x ≤ 1,

u (0,t)=0,u(1,t)=0,t≥ 0.

16. Determine the solution of th e initial boundary-value problem

= c

, 0 <x<l, t>0,

u (x , 0) = f (x) , 0 ≤ x ≤ l,

(x, 0) = g (x) , 0 ≤ x ≤ l,

(0,t)=0,u

(l, t)=0,t≥ 0,

by extending f and g as even functions about x = 0 and x = l.

17. Determine the solution of th e initial boundary-value problem

= c

, 0 <x<l, t>0,

u (x , 0) = f (x) , 0 ≤ x ≤ l,

(x, 0) = g (x) , 0 ≤ x ≤ l,

u (0,t)=p (t) ,u(l, t)=q (t) ,t≥ 0.

162 5 The Cauchy Problem and Wave Equations

18. Determine the solution of th e initial boundary-value problem

= c

, 0 <x<l, t>0,

u (x , 0) = f (x) , 0 ≤ x ≤ l,

(x, 0) = g (x) , 0 ≤ x ≤ l,

(0,t)=p (t) ,u

(l, t)=q (t) ,t≥ 0.

19. Solve the characteristic initi al-value problem

− x

− y

+ x

=0,

u (x , y)=f (x)ony

− x

=8 for 0≤ x ≤ 2,

u (x , y)=g (x)ony

+ x

= 16 for 2 ≤ x ≤ 4,

with f (2) = g (2).

20. Solve the Goursat problem

− x

− y

+ x

=0,

u (x , y)=f (x)ony

+ x

= 16 for 0 ≤ x ≤ 4,

u (x , y)=g (y)onx =0 for 0≤ y ≤ 4,

where f (0) = g (4).

21. Solve

= c

u (x , t)=f (x)ont = t (x) ,

u (x , t)=g (x)onx + ct =0,

where f (0) = g (0).

22. Solve the characteristic initi al-value problem

− x

− u

=0,x=0,

u (x , y)=f (y)ony −

=0 for 0≤ y ≤ 2,

u (x , y)=g (y)ony +

=4 for 2≤ y ≤ 4,

where f (2) = g (2).

23. Solve

+10u

+9u

=0,

u (x , 0) = f (x) ,

(x, 0) = g (x) .

5.12 Exercises 163

24. Solve

4 u

+5u

+ u

=2,

u (x , 0) = f (x) ,

(x, 0) = g (x) .

25. Solve

3 u

+10u

+3u

=0,

u (x , 0) = f (x) ,u

(x, 0) = g (x) .

26. Solve

− 3 u

+2u

=0,

u (x , 0) = f (x) ,u

(x, 0) = g (x) .

27. Solve

− t

=0 x>0,t>0,

u (x , 1) = f (x) ,

(x, 1) = g (x) .

28. Consider the initial boundary-value problem for a string of length l

under the action of an external force q (x, t) per unit length. The dis-

placement u (x, t) satisﬁes the wave equation

ρu

= Tu

+ ρq(x, t) ,

where ρ is the line density of the string and T is the constant tension

of the string. The initial and boundary conditions of the p rob lem are

u (x , 0) = f (x) ,u

(x, 0) = g (x) , 0 ≤ x ≤ l,

u (0,t)=u (l, t)=0,t>0.

Show that the energy equation is

=[Tu

]



ρqu

dx,

where E represents the energy integral

E (t)=





ρu

+ Tu



dx.

Explain the physical signiﬁcance of the energy equation.

Hence or otherwise, derive the principle of conservation of energy, that

is, that the total energy is constant for all t ≥ 0 provided that the string

has free or ﬁxed ends and there are no external forces.

164 5 The Cauchy Problem and Wave Equations

29. Show that the solution of the signaling problem governed by the wave

equation

= c

,x>0,t>0,

u (x , 0) = u

(x, 0) = 0,x>0,

u (0,t)=U (t) ,t>0,

u (x , t)=U



t −





t −



where H is the Heavisid e unit step function.

30. Obtain the solution of the initial-value problem of the homogeneous

wave equation

− c

=sin(kx − ωt) , −∞ <x<∞,t>0,

u (x , 0) = 0 = u

(x, 0) , for all x ∈ R,

where c, k and ω are constants.

Discuss the non-resonance case, ω = ck and the resonance case, ω = ck.

31. In each of the following Cauchy problems, obtain the solution of the

system

− c

=0,x∈ R,t>0,

u (x , 0) = f (x)andu

(x, 0) = g (x)forx ∈ R,

for the given c, f (x)andg (x):

(a) c =3, f (x)=cosx, g (x)=sin2x.

(b) c =1, f (x)=sin3x, g (x)=cos3x.

(d) c =2, f (x) = cosh x, g (x)=2x.

(e) c =3, f (x)=x

, g (x)=x cos x.

(f) c =4, f (x)=cosx, g (x)=xe

−x

32. If u (x, t) is the solution of the nonhomogeneous Cauchy problem

− c

= p (x, t) , for x ∈ R,t>0,

u (x , 0) = 0 = u

(x, 0) , for x ∈ R,

5.12 Exercises 165

and if v (x, t, τ) is the solution of th e nonhomogeneous Cauchy problem

− c

=0, for x ∈ R,t>0,

v (x, 0; τ )=0,v

(x, 0; τ )=p (x, τ) ,x∈ R,

show that

u (x , t)=



v (x, t; τ ) dτ.

This is known as the Duhamel principle for the wave equation.

33. Show that the solution of the nonhomogeneous diﬀusion equation with

homogeneous boundary and initial data

= κu

+ p (x, t) , 0 <x<l, t>0,

u (0,t)=0=u (l, t) ,t>0,

u (x , 0) = 0, 0 <x<l,

u (x , t)=



v (x, t; τ ) dτ,

where v = v (x, t; τ ) satisﬁes the h omogeneous diﬀusion equation with

nonhomogeneous boundary and initial data

= κv

+ p (x, t) , 0 <x<l, t>0,

v (0,t; τ )=0=v (l, t; τ ) ,t>0,

v (x, τ ; τ )=p (x, τ) .

This is known as the Duhamel principle for the diﬀusion equation.

34. Use the Duhamel principle to solve the nonhomogeneous diﬀusion equa-

tion

= κu

+ e

−t

sin πx, 0 <x<l, t>0,

with the homogeneous boundary and initial data

u (0,t)=0,u(1,t)=0,t>0,

u (x , 0) = 0, 0 ≤ x ≤ 1.

35. (a) Verify that

(x, y)=exp



ny −

√



sin nx,

is the solution of the Laplace equation

166 5 The Cauchy Problem and Wave Equations

+ u

=0,x∈ R,y>0,

u (x , 0) = 0,u

(x, 0) = n exp



−

√



sin nx,

where n is a positive integer.

(b) Show that this Cauchy problem is not well posed.

36. Show that the following Cauchy problems are not well posed:

(a) u

= u

,x∈ R,t>0,

u (0,t)=





sin





(0,t)=0,t>0.

(b) u

+ u

=0,x∈ R,t>0,

(x, 0) → 0, (u

)

(x, 0) → 0, as n →∞.

Fourier Series and Integrals with Applications

“The th orough study of nature is the most ground for mathematical dis-

coveries.”

Joseph Fourier

“Nearly ﬁfty years had passed without any progress on the question of an-

alytic representation of an arbitrary function, when an assertion of Fourier

threw new light on the subject. Thus a new era began for the development

of this part of Mathematics and this was heralded in a stunning way by

major developments in mathematical Physics.”

Bernhard Riemann

“Fourier created a coherent metho d by which the diﬀerent components of

an equation and its solution in series were neatly identiﬁed with diﬀerent

aspects of physical solution being analyzed. He also had a uniquely sure

instinct for interpreting the asymptotic properties of the solutions of his

equations f or their physical meaning. So powerful was his appr oach that

a full century passed before non-linear equations regained prominence i n

mathematical physics.”

Ioan James

6.1 Introduction

This chapter is devoted to the theory of Fourier series and integrals. Al-

though the treatment can be extensive, the exposition of the theory here

will be concise, but suﬃcient for its application to many problems of applied

mathematics and mathematical physics.

168 6 Fourier Series and Integrals with Applications

The Fourier theory of trigonometric series is of great practical impor-

tance because certain types of discontinuous functions which cannot be ex-

panded in power series can be expanded in Fourier series. M ore importantly,

a wide class of problems in physics and engineering possesses periodic phe-

nomena and, as a consequence, Fourier’s trigonometric series b ecome an

indispensable tool in the an alysis of these problems.

We shall begin our study with the basic concepts and d eﬁn ition s of some

properties of real-valued functions.

6.2 Piecewise Continuous Functions and Periodic

Functions

A single-valued function f is said to be piecewise continuous in an interval

[a, b] if there exist ﬁnitely many points a = x

<...<x

= b,such

that f is continuous in the intervals x

<x<x

j+1

and the one-sided limits

f (x

+) and f (x

j+1

−) exist for all j =1, 2, 3,...,n− 1.

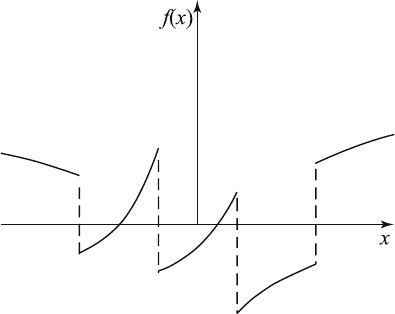
A piecewise continuous function is shown in Figure 6.2.1. Functions such

as 1/x and sin (1/x) fail to be piecewise continu ou s in the closed interval

[0, 1] because the one-sided limit f (0+) does not exist in either case.

If f is piecewise continuous in an interval [a, b], then it is necessarily

bounded and integrable over that interval. Also, it follows immediately that

the product of two piecewise continu ous functions is p iecewise continuous

on a common interval.

If f is piecewise continuous in an interval [a, b] and if, in addition, the

ﬁrst derivative f

′

is continuous in each of the intervals x

<x<x

j+1

and the limits f

′

+) and f

′

−) exist, then f is said to be piecewise

smooth; if, in addition, the second derivative f

′′

is continu ous in each of

Figure 6.2.1 Graph of a Piecewise Continuous Function.

6.2 Piecewise Continuous Functions and Periodic Functions 169

the intervals x

<x<x

j+1

, and the limits f

′′

+) and f

′′

−) exist,

then f is said to be piecewise very smooth.

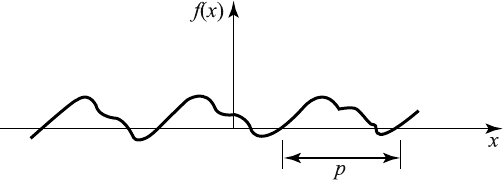
A piecewise continuous function f (x)inaninterval[a, b] is said to be

periodic if there exists a real positive number p such that

f (x + p)=f (x) , (6.2.1)

for all x, p is called the period of f, and the smallest value of p is termed

the fundamental period. A sample graph of a periodic function is given in

Figure 6.2.2.

If f is periodic with period p,then

f (x + p)=f (x) ,

f (x +2p)=f (x + p + p)=f (x + p) ,

f (x +3p)=f (x +2p + p)=f (x +2p ) ,

f (x + np)=f (x +(n − 1) p + p)=f (x +(n − 1) p)=f (x) ,

for any integer n. Hence, for all integral values of n

f (x + np)=f (x) . (6.2.2)

It can be readily shown that if f

, f

, ..., f

have the period p and c

are the constants, then

f = c

+ c

+ ...+ c

, (6.2.3)

has the period p.

Well known examples of periodic functions are the sine and cosine func-

tions. As a special case, a constant f unction is also a periodic function with

arbitrary period p. Thu s, by the relation (6.2.3), the series

+ a

cos x + a

cos 2x + ...+ b

sin x + b

sin 2x + ...

if it converges, obviously has the period 2π. Such types of series, which occur

frequently in problems of applied mathematics and mathematical physics,

will be treated later.

Figure 6.2.2 Periodic Function.

170 6 Fourier Series and Integrals with Applications

6.3 Systems of Orthogonal Functions

A sequence of functions {φ

(x)} is said to be orthogonal with respect to

the weight function q (x) on the interval [a, b]if



(x) φ

(x) q (x) dx =0,m= n. (6.3.1)

If m = n,thenwehave

φ

 =





(x) q (x) dx



(6.3.2)

which is called the norm of the orthogonal system {φ

(x)}.

Example 6.3.1. The sequence of functions {sin mx}, m =1, 2,..., form an

orthogonal system on the interval [−π,π], because



−π

sin mx sin nx dx =

⎧

⎨

⎩

0,m= n,

π, m = n.

In this example we notice that the weight function is equal to unity, and

the value of the norm is

√

π.

An orthogonal system φ

, φ

, ..., φ

,wheren may be ﬁnite or inﬁnite,

which satisﬁes the relations



(x) φ

(x) q (x) dx =

⎧

⎨

⎩

0,m= n,

1,m= n,

(6.3.3)

is called an orthonormal system of functions on [a, b]. It is evident that an

orthonormal system can be obtained from an orthogonal system by dividing

each function by its nor m on [a, b].

Example 6.3.2. The sequence of functions

1, cos x, sin x,...,cos nx, sin nx

forms an orthogonal system on [−π, π]since



−π

sin mx sin nx dx =

⎧

⎨

⎩

0,m= n,

π, m = n,



−π

sin mx cos nx dx =0, for all m, n, (6.3.4)



−π

cos mx cos nx dx =

⎧

⎨

⎩

0,m= n,

π, m = n,