Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

5.7 Nonhomogeneous Wave Equations 141



− u

) dR =



dy + u

dx) . (5.7.8)

Since B is composed of B

, B

,andB

, we note that



dy + u

dx)=



−y

dx,



dy + u

dx)=



(−u

dx − u

dy) ,

= u (x

+ y

, 0) − u (x

) ,



dy + u

dx)=



dx + u

dy) ,

= u (x

− y

, 0) − u (x

) .

Hence,



dy + u

dx)=−2 u (x

)+u (x

− y

, 0)

+u (x

+ y

, 0) +



−y

dx. (5.7.9)

Combining equations (5.7.7), (5.7.8) and (5.7.9), we obtain

u (x

[u (x

+ y

, 0) + u (x

− y

, 0)]



−y

dx −



h (x, y) dR. (5.7.10)

We have chosen x

, y

arbitrarily, and as a consequence, we replace x

x and y

by y. Equation (5.7.10) thus becomes

u (x , y)=

[f (x + y)+f (x − y)] +



x+y

x−y

g (τ) dτ −



h (x, y) dR.

In terms of the original variables

u (x , t)=

[f (x + ct)+f (x − ct)] +



x+ct

x−ct

∗

(τ) dτ −



h (x, t) dR.

(5.7.11)

Example 5.7.1. Determine the solution of

− u

=1,

u (x , 0) = sin x,

(x, 0) = x.

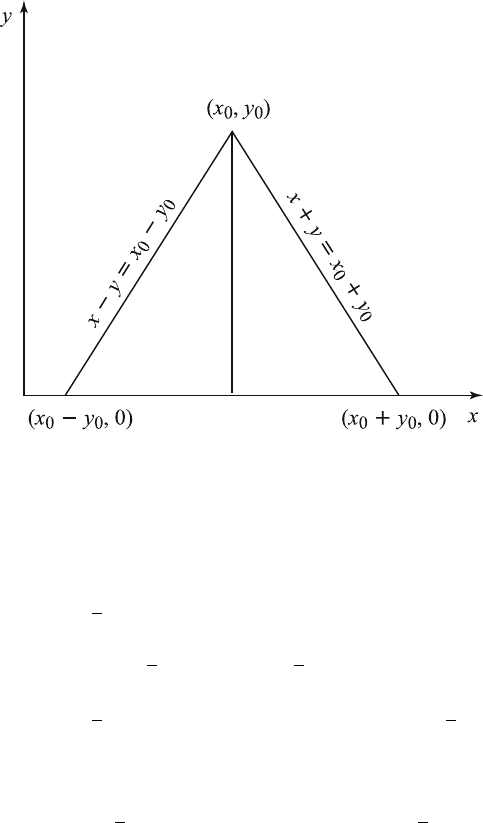
142 5 The Cauchy Problem and Wave Equations

Figure 5.7.2 Triangular Region.

It is easy to see that the characteristics are x + y = constant = x

+ y

and

x − y = constant = x

− y

, as shown in Figure 5.7.2. Thus,

u (x

[sin (x

+ y

)+sin(x

− y

)]



−y

τdτ−



−y +x

y +x

−y

dx dy

[sin (x

+ y

)+sin(x

− y

)] + x

−

Now dropping the subscript zero, we obtain the solution

u (x , y)=

[sin (x + y)+sin(x − y)] + xy −

5.8 The Riemann Method

We shall discuss Riemann’s method of i ntegrating the linear hyperbolic

equation

L [u] ≡ u

+ au

+ bu

+ cu = f (x, y) , (5.8.1)

5.8 The Riemann Method 143

where L denotes the linear operator, and a (x, y), b (x, y), c (x, y), and

f (x, y) are diﬀerentiable functions in some domain D

∗

. The method con-

sists essentially of the derivation of an integral formula which represents

the solution of the Cauchy problem.

Let v (x, y) be a function having continuous second-order partial deriva-

tives. Then, we may write

− uv

=(vu

)

− (vu

)

vau

=(avu)

− u (av)

, (5.8.2)

vbu

=(bvu)

− u (bv)

so that

vL [u] − uM [v]=U

+ V

, (5.8.3)

where M is the operator represented by

M [v]=v

− (av)

− (bv)

+ cv, (5.8.4)

and

U = auv − uv

,V= buv + vu

. (5.8.5)

The operator M is called the adjoint operator of L.IfM = L, then the

operator L is said to be self-adjoint. Now ap pl ying Green’s theorem, we

have



+ V

) dx dy =



(Udy− Vdx) , (5.8.6)

where C is the closed curve bounding the region of integration D which is

in D

∗

Let Λ be a smooth initial curve which is continuous, as shown in Figure

5.8.1. Since equation (5.8.1) is in ﬁrst canonical form, x and y are the

characteristic coordinates. We assume that the tangent to Λ is nowhere

parallel to the x or y axis. Let P (α, β)beapointatwhichthesolutionto

the Cauchy problem is sought. Line PQ parallel to the x axis intersects the

initial curve Λ at Q, and line PR parallel to the y axis intersects the curve

Λ at R. We suppose that u and u

or u

are prescribed along Λ.

Let C be th e closed contour PQRP bounding D.Sincedy =0onPQ

and dx =0onPR, it follows immediately from equations (5.8.3) and (5.8.6)

that



(vL [u] − uM [v]) dx dy =



(Udy− Vdx)+



Udy−



Vdx.

(5.8.7)

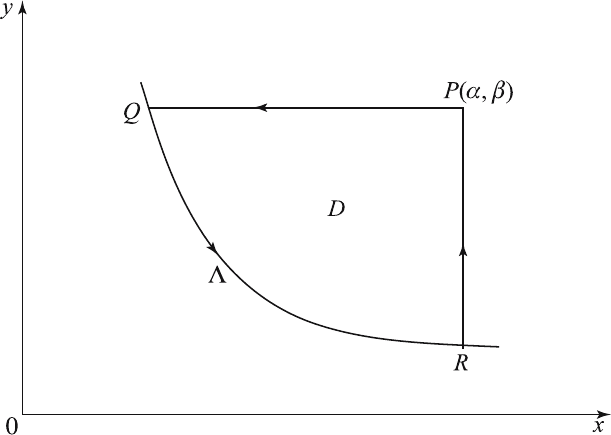
144 5 The Cauchy Problem and Wave Equations

Figure 5.8.1 Smooth initial curve.

From equation (5.8.5), we ﬁnd



Vdx=



bvu dx +



dx.

Integrating by parts, we obtain



dx =[uv]

−



dx.

Hence, we may write



Vdx=[uv]



u (bv − v

) dx.

Substitution of this integral in equation (5.8.7) yields

[uv]

=[uv]



u (bv − v

) dx −



u (a v − v

) dy −



(Udy− Vdx)



(vL [u] − uM [v]) dx dy. (5.8.8)

Suppose we can choose the function v (x, y; α, β) to be the solution of

the adjoint equation

5.8 The Riemann Method 145

M [v]=0, (5.8.9)

satisfying the conditions

= bv when y = β,

= av when x = α, (5.8.10)

v =1 when x = α and y = β.

The function v (x, y; α, β) is called the Riemann function.SinceL [u]=f,

equation (5.8.8) reduces to,

[u]

=[uv]

−



uv (ady− bdx)+



(uv

dy + vu

dx)+



vf dx dy.

(5.8.11)

Thisgivesusthevalueofu at the point P when u and u

are prescribed

along the curve Λ.Whenu and u

are prescribed, the identity

[uv]

− [uv]



(

(uv)

dx +(uv)

)

may be used to put equation (5.8.8) in the form

[u]

=[uv]

−



uv (ady− bdx) −



(uv

dx + vu

dy)



vf dx dy. (5.8.12)

By adding equations (5.8.11) and (5.8.12), the value of u at P is given by

[u]



[uv]

+[uv]



−



uv (ady− bdx) −



u (v

dx − v

dy)



v (u

dx − u

dy)+



vf dx dy (5.8.13)

which is the solution of the Cauchy problem in terms of the Cauchy data

given along th e curve Λ. It is easy to see that the solution at the point

(α, β) depends only on the Cauchy data along the arc QR on Λ.Ifthe

initial data were to change outside this arc QR, the solution would change

only outside the triangle PQR. Thus, from Figure 5.8.2, we can see that

each characteristic separates the region in which the solution remains un-

changed from the region in which it varies. Because of th is fact, the unique

continuation of the solution across any characteristic is not possible. This

is evident from Figure 5.8.2. The solution on the right of the characteristic

is determined by the initial data given in Q

, whereas the solution

146 5 The Cauchy Problem and Wave Equations

Figure 5.8.2 Solution on the right and left of the characteristic.

on the left is determined by the initial data given on Q

. If the initial

data on R

were changed, the solution on the right of P

only will be

aﬀected.

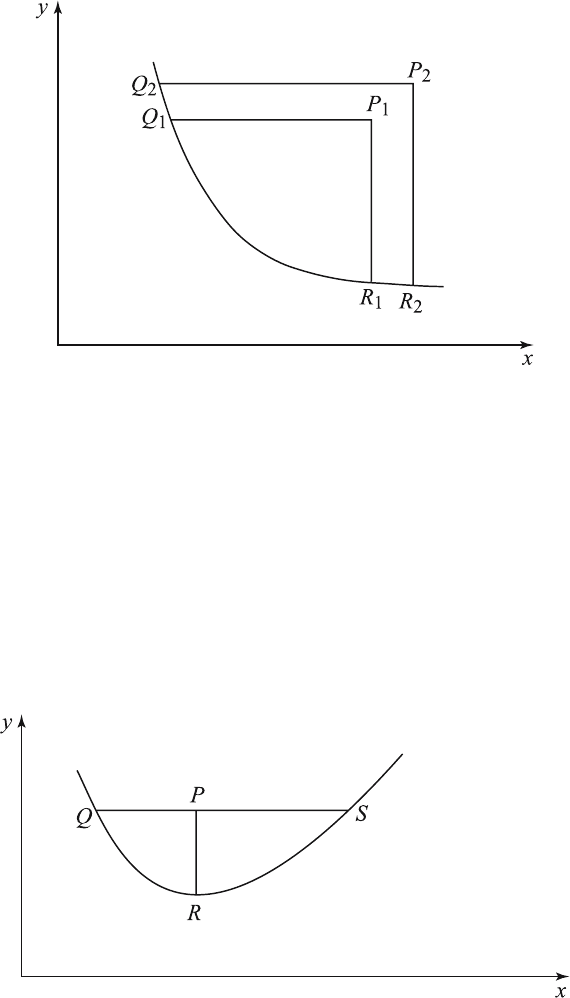
It should be remarked here that the initial curve can intersect each

characteristic at only one point. Suppose, for example, the ini tial curve Λ

intersects the characteristic at two points, as shown in Figure 5.8.3. Then,

the solution at P obtained from the initial data on QR will be diﬀerent

from the solution obtained from the initial data on RS. Hence, the Cauchy

problem, in this case, is not solvable.

Figure 5.8.3 Initial curve intersects the characteristic at two points.

5.8 The Riemann Method 147

Example 5.8.1. The telegraph equation

+ a

∗

+ b

∗

w = c

may be transformed into canonical form

L [u]=u

ξη

+ ku =0,

by the successive transformations

w = ue

−a

∗

t/2

and

ξ = x + ct, η = x − ct,

where k =



∗2

− 4b

∗



/16c

We apply Riemann’s method to determine the solution satisfying the

initial conditions

u (x , 0) = f (x) ,u

(x, 0) = g (x) .

Since

t =

(ξ − η) ,

the line t = 0 corresponds to the straight line ξ = η in the ξ −η plane. The

initial conditions may thus be transformed into

[u]

ξ=η

= f (ξ) , (5.8.14)

− u

]

ξ=η

= c

−1

g (ξ) . (5.8.15)

We next determine the Riemann function v (ξ, η; α, β) which satisﬁes

ξη

+ kv =0, (5.8.16)

(ξ,β; α, β)=0, (5.8.17)

(α, η; α, β)=0, (5.8.18)

v (α, β; α, β)=1. (5.8.19)

The diﬀerential equation (5.8.16) is self-adjoint, that is,

L [v]=M [v]=v

ξη

+ kv.

We assume that the Riemann function is of the form

v (ξ,η; α, β)=F (s) ,

with the argument s =(ξ − α)(η − β). Substituting this value in equation

(5.8.16), we obtain

148 5 The Cauchy Problem and Wave Equations

+ F

+ kF =0.

If we let λ =

√

4ks, the above equation becomes

′′

(λ)+

′

(λ)+F (λ)=0.

This is the Bessel equation of order zero, and the solution is

F (λ)=J

(λ) ,

disregarding Y

(λ) which is unbounded at λ = 0. Thus, the Riemann func-

tion is

v (ξ,η; α, β)=J





4k (ξ − α)(η − β)



which satisﬁes equation (5.8.16) and is equal to one on the characteristics

ξ = α and η = β.SinceJ

′

(0) = 0, equations (5.8.17) and (5.8.18) are

satisﬁed. From this, it immediately follows that

]

ξ=η

√

k (ξ − β)



(ξ − α)(η − β)

′

(λ)]

ξ=η

]

ξ=η

√

k (ξ − α)



(ξ − α)(η − β)

′

(λ)]

ξ=η

Thus, we have

− u

]

ξ=η

√

k (α − β)



(ξ − α)(ξ − β)

′

(λ)]

ξ=η

. (5.8.20)

From the initial condition

u (Q)=f (β)andu (R)=f (α) , (5.8.21)

and substituting equations (5.8.15) , (5.8.19), and (5.8.20) into equation

(5.8.13), we obtain

u (α, β)=

[f (α)+f (β)]

−



√

k (α − β)



(τ − α)(τ − β)

′





4k (τ −α)(τ − β)



f (τ) dτ







4k (τ −α)(τ − β)



g (τ) dτ. (5.8.22)

Replacing α and β by ξ and η, and substituti ng the original variables x and

t, we obtain

5.9 Solution of the Goursat Problem 149

u (x , t)=

[f (x + ct)+f (x − ct)] +



x+ct

x−ct

G (x, t, τ ) dτ, (5.8.23)

where

G (x, t, τ )

−2

√

kctf(τ ) J





(τ − x)

− c

0

(τ − x)

− c

+ c

−1

g (τ) J





(τ − x)

− c



If we set k = 0, we arrive at the d’Alembert solution for the wave equation

u (x , t)=

[f (x + ct)+f (x − ct)] +



x+ct

x−ct

g (τ) dτ.

5.9 Solution of the Goursat Problem

The Goursat problem is that of ﬁnding the solution of a linear hyperbolic

equation

= a

(x, y) u

+ a

(x, y) u

+ a

(x, y) u + h (x, y) , (5.9.1)

satisfying the prescribed conditions

u (x , y)=f (x) , (5.9.2)

on a characteristic, say, y =0,and

u (x , y)=g (x) (5.9.3)

on a monotonic increasing curve y = y (x) which, for simplicity, is assumed

to intersect the characteristic at the origin.

The solution in the region between the x-axis and the monotonic curve

in the ﬁrst quadrant can be determined by the method of successive ap-

proximations. The proof is given in Garabedian (1964).

Example 5.9.1. Determine the solution of the Goursat problem

= c

, (5.9.4)

u (x , t)=f (x) , on x − ct =0, (5.9.5)

u (x , t)=g (x) , on t = t (x) , (5.9.6)

where f (0) = g (0).

150 5 The Cauchy Problem and Wave Equations

The general solution of the wave equation is

u (x , t)=φ (x + ct)+ψ (x − ct) .

Applying the prescribed conditions, we obtain

f (x)=φ (2x)+ψ (0) , (5.9.7)

g (x)=φ (x + ct(x)) + ψ (x − ct(x)) . (5.9.8)

It is evident that

f (0) = φ (0) + ψ (0) = g (0) .

Now, if s = x − ct(x), the inverse of it is x = α (s). Thus, equation (5.9.8)

may be written as

g (α (s)) = φ (x + ct(x)) + ψ (s) . (5.9.9)

Replacing x by (x + ct(x)) /2 in equation (5.9.7), we obtain



x + ct(x)



= φ (x + ct(x)) + ψ (0) . (5.9.10)

Thus, using (5.9.10), equation (5.9.9) becomes

ψ (s)=g (α (s)) − f



α (s)+ct(α (s))



+ ψ (0) .

Replacing s by x − ct ,wehave

ψ (x − ct)=g (α (x − ct)) − f



α (x − ct)+ct(α (x − ct))



+ ψ (0) .

Hence, the solution is given by

u (x , t)=f



x + ct



− f



α (x − ct)+ct(α (x − ct))



+ g (α (x − ct)) .

(5.9.11)

Let us consider a special case when the curve t = t (x) is a straight line

represented by t − k x = 0 with a constant k>0. Then s = x − ckx and

hence x = s/ (1 − ck). Using these values in (5.9.11), we obtain

u (x , t)=f



x + ct



− f



(1 + ck)(x − ct)

2(1− ck)



+ g



x − ct

1 − ck



. (5.9.12)

When the values of u are prescribed on both characteristics, the prob lem

of ﬁnding u of a linear hyperbolic equation is called a characteristic initial-

value problem. This is a degenerate case of the Goursat problem.