Myint Tyn U., Debnath L. Linear Partial Differential Equations for Scientists and Engineers

Подождите немного. Документ загружается.

6.10 The Riemann–Lebesgue Lemma and Pointwise Convergence Theorem 201

Example 6.9.5. From the solution to problem 25 in 6.14 Exercises, we obtain

the complex Fourier series of f (t)in−l<t<l.

We use the transformation x =

in Exercise 25 so that

−



π +





π −



⎫

⎬

⎭



n=0

exp



inlt



6.10 The Riemann–Lebesgue Lemma and Pointwise

Convergence Theorem

We have stated earlier that if f (x) is piecewise continuous on the interval

[−π, π], then there exists a Fourier series expansion which converges in the

mean to f (x).

In this section, we shall discuss the Pointwise Convergence Theorem

with a proof using the Riemann–Lebesgue Lemma.

Lemma 6.10.1. (Riemann–Lebesgue Lemma) If g (x) is piecewise con-

tinuous on the interval [a, b], then

lim

λ→∞



g (x)sinλx dx =0. (6.10.1)

Proof. Consider the integral

I (λ)=



g (x)sinλx dx. (6.10.2)

With the change of variable

x = t + π/λ,

we have

sin λx =sinλ (t + π/λ)=−sin λt,

and

I (λ)=−



b−π/λ

a−π/λ

g (t + π/λ)sinλt dt. (6.10.3)

Since t is a dummy variable, we write the above integral as

I (λ)=−



b−π/λ

a−π/λ

g (x + π/λ)sinλx dx. (6.10.4)

Addition of equations (6.10.2) and (6.10.4) yields

202 6 Fourier Series and Integrals with Applications

2I (λ)=



g (x)sinλx dx −



b−π/λ

a−π/λ

g (x + π/λ)sinλx dx

= −



a−π/λ

g (x + π/λ)sinλx dx +



b−π/λ

g (x)sinλx dx



b−π/λ

[g (x) − g (x + π/λ)] sin λx dx. (6.10.5)

First, let g (x) be a continuous function in [a, b]. Then g (x) is necessarily

bounded, that is, there exists an M such that |g (x)|≤M. Hence,





a−π/λ

g (x + π/λ)sinλx dx





a+π/λ

g (x)sinλx dx



≤

πM

and





b−π/λ

g (x)sinλx dx



≤

πM

Consequently,

|I (λ)|≤

πM



b−π/λ

|g (x) − g (x + π/λ)|dx. (6.10.6)

Since g (x) is a continuous function on a closed interval [a, b], it is uniformly

continuous on [a, b]sothat

|g (x) − g (x + π/λ)| <ε/(b − a) , (6.10.7)

for all λ>Λand all x in [a, b]. We now choose λ such that πM /λ < ε/2,

whenever λ>Λ.Then

|I (λ)| <

= ε.

If g (x) is piecewise continuous in [a, b], then the proof consists of a

repeated application of the preceding argument to every subinterval of [a, b]

in which g (x) is continuous.

Theorem 6.10.1. (Pointwise Convergence Theorem). If f (x) is piece-

wise smooth and periodic function with period 2π in [−π, π],thenforany

∞



k=1

cos kx + b

sin kx)=

[f (x+) + f (x−)] , (6.10.8)

where



−π

f (t)coskt dt, k =0, 1, 2,..., (6.10.9)



−π

f (t)sinkt dt, k =1, 2, 3,.... (6.10.10)

6.10 The Riemann–Lebesgue Lemma and Pointwise Convergence Theorem 203

Proof. The nth partial sum s

(x) of the series (6.10.8) is

(x)=



k=1

cos kx + b

sin kx) . (6.10.11)

We use integrals in (6.10.9)–(6.10.10) to replace a

and b

in (6.10.11)

so that

(x)=

2π



−π



1+2



k=1

(cos kt cos kx +sinkt sin kx)



f (t) dt

2π



−π



1+2



k=1

cos k (x − t)



f (t) dt

2π



−π

(x − t) f (t) dt, (6.10.12)

where D

(θ) i s called the Dirichlet kernel deﬁned by

(θ)=1+2



k=1

cos kθ. (6.10.13)

ThenextstepistostudythepropertiesofthiskernelD

(θ)whichis

an even function with period 2π and satisﬁes the condition

2π



−π

(θ) dθ =1+0+0+...+0=1. (6.10.14)

We ﬁnd the value of the sum in (6.10.13) by Euler’s formula so that

(θ)=1+



k=1



ikθ

+ e

−ikθ





k=−n

ikθ

= e

−inθ

+ ...+1+...+ e

inθ

This is a ﬁnite geometric series with the ﬁrst term e

−inθ

, the ratio e

iθ

,and

the last term e

inθ

, and hence, its sum is given by

(θ)=

−inθ

− e

i(n+1)θ

1 − e

iθ

exp

−



n +



iθ

− exp



n +



iθ

exp



−

iθ



− exp



iθ



sin



n +



sin

. (6.10.15)

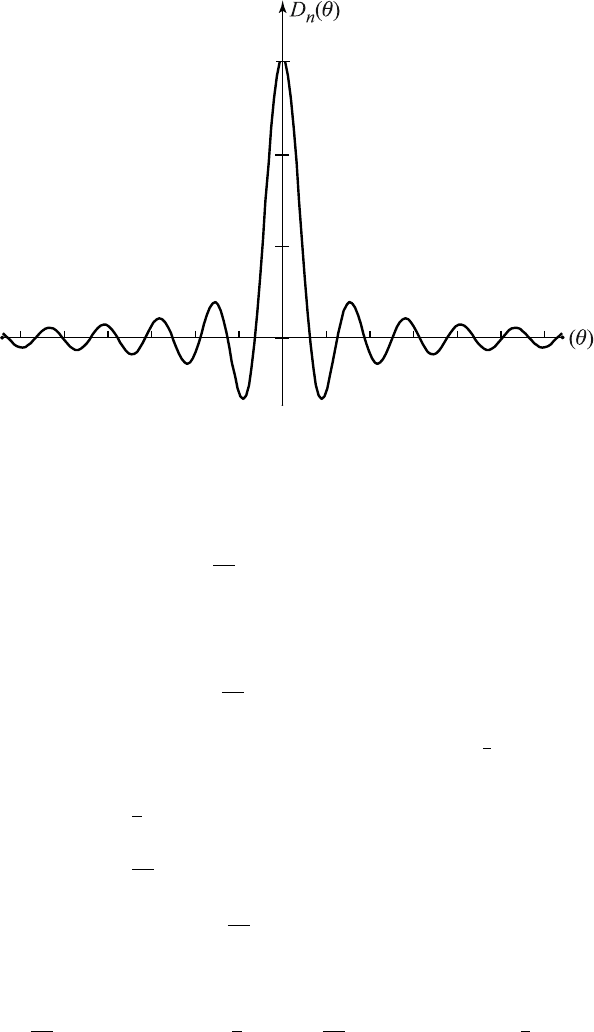
The graph of D

(θ) is shown in Figure 6.10.1. It looks similar to that of

the diﬀusion kernel as drawn in Figure 12.4.1 in Chapter 12 except for its

symmetric oscillatory trail.

204 6 Fourier Series and Integrals with Applications

Figure 6.10.1 Graph of D

(θ ) against θ.

We next put t − x = θ in (6.10.12) to obtain

(x)=

2π



x+π

x−π

(θ) f (x + θ) dθ. (6.10.16)

Since both D

and f have period 2π, the limits of the integral can be taken

from −π to π, and hence, (6.10.16) assumes the form

(x)=

2π



−π

(θ) f (x + θ) dθ. (6.10.17)

We next use (6.10.14) to express the diﬀerence of s

(x)and

[f (x+) + f (x−)]

in the form

(x) −

[f (x+) + f (x−)]

2π



−π

(θ)[f (x + θ) − f (x−)] dθ

2π



(θ)[f (x + θ) − f (x+)] dθ

which is, by (6.10.15),

2π



−π

−

(θ)sin



n +



θdθ+

2π



(θ)sin



n +



θdθ,

(6.10.18)

6.10 The Riemann–Lebesgue Lemma and Pointwise Convergence Theorem 205

where

(θ)=



sin



−1

[f (x + θ) − f (x +

)] . (6.10.19)

Since the denominators of the functions g

(θ) vanish at θ =0,inte-

grals in (6.10.18) may diverge at this point. However, by assumption, f is

piecewise smooth, and hence,

lim

θ→0+

(θ) = lim

θ→0+

f (x + θ) − f (x)



sin



=2f

′

(x +

) .(6.10.20)

Evidently, the above limits exist, and g

(θ) are piecewise continuous else-

where in the interval (−π, π). Therefore, by the Riemann–Lebesgue Lemma

6.10.1, both integrals in (6.10.18) vanish as n →∞.Thus,

lim

n→∞

(x)=

[f (x+) + f (x−)] .

This proves that the Fourier series converges for each x in (−π, π).

Remark 3. At a point of continuity the series converges to the function

f (x).

Remark 4. At a point of discontinuity, the series is equal to the arithmetic

mean of the limits of the function on both sides of the discontinuity.

Remark 5. The condition of piecewise smoothness under which the Fourier

series converges pointwise is a su ﬃcient condition. A large number of ex-

amples of applications is covered by this case. However, the pointwise con-

vergence Theorem 6.10.1 can be proved under weaker conditions.

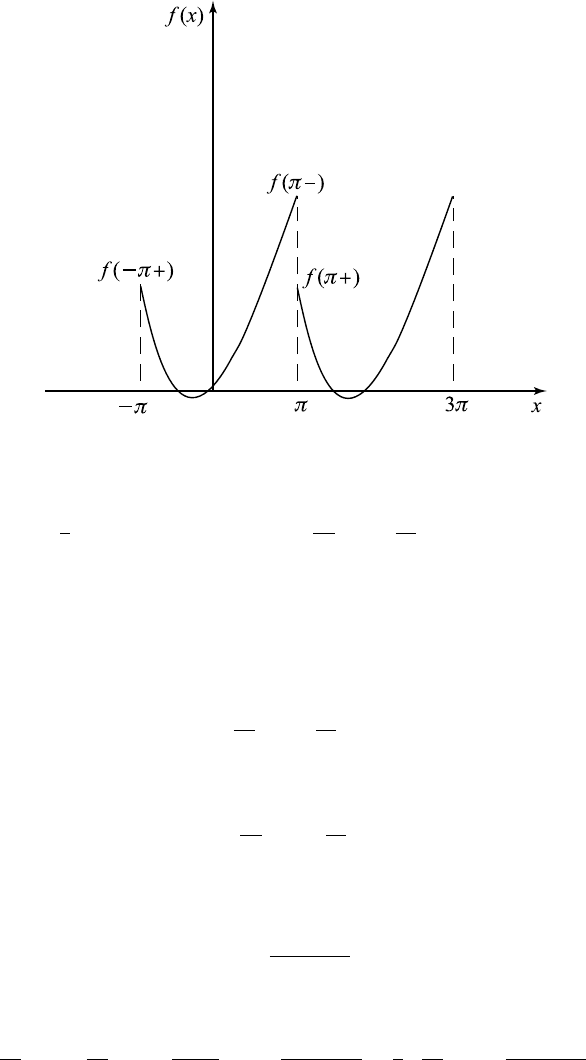
Example 6.10.1. In Example 6.6.1, we obtained that the Fourier series ex-

pansion for



x + x



in [−π,π], as shown in Figure 6.10.2, is

f (x) ∼

∞



k=1



(−1)

cos kx −

(−1)

sin kx



Since f (x)=x + x

is piecewise smooth, the series converges, and hence,

we write

x + x

∞



k=1



(−1)

cos kx −

(−1)

sin kx



at points of continuity. At points of discontinuity, such as x = π,byvirtue

of the Pointwise Convergence Theorem,

206 6 Fourier Series and Integrals with Applications

Figure 6.10.2 Graph of f (x).



π + π





−π + π

!

∞



k=1

(−1)

cos kπ, (6.10.21)

since

f (π−)=π + π

and f (π+) = f (−π+) = −π + π

Simpliﬁcation of equation (6.10.21) gives

∞



k=1

(−1)

∞



k=1

The series can be used to obtain the sum of reciprocals of squares of odd

positive integers, that is,

∞



n=1

(2n − 1)

We have

∞



n=1

∞



n=1

(2n)

∞



n=1

(2n − 1)

∞



n=1

(2n − 1)

6.10 The Riemann–Lebesgue Lemma and Pointwise Convergence Theorem 207

or,

∞



n=1

(2n − 1)



1 −



Conversely, this series can be used t o ﬁnd the sum of reciprocals of squares

of all positive integers.

Example 6.10.2. Find the Fourier series of the following function

f (x)=

⎧

⎨

⎩

0, −2 ≤ x<0

2 − x, 0 <x≤ 2.

This fu nction is deﬁned over the interval −2 ≤ x ≤ 2, where it is piecewise

smooth with a ﬁnite discontinuity at x = 0. We use (6.9.7) and (6.9.8) to

calculate the Fourier coeﬃcients



(2 − x) dx =1



(2 − x)cos



πkx



dx =

1 − (−1)

,k=1, 2, 3,....



(2 − x)sin



πkx



dx =

πk

,k=1, 2, 3,....

Consequently, the Fourier series (6.9.6) becomes

f (x)=

∞



k=1

⎡

⎣

(

1 − (−1)

)

πk

cos



πkx



sin



πkx



⎤

⎦

. ( 6.10.22)

The function f (x) is continuous at x =1wheref (1) = 1, so that the

Fourier series (6.10.22) gives

∞



n=1



{1 − (−1)

}

πn

cos



nπ



sin



nπ





Since the factor 1 − (−1)

=0forevenn,andcos

nπ

=0whenn is

odd, every term of the cosine series vanishes for all n. Consequently,

∞



n=1

sin



nπ



∞



n=1

(−1)

(2n +1)

. (6.10.23)

On the other hand, f (x) is discontinuous at x = 0 and the Fou rier series

must converge to

(0 + 2) = 1. Thus,

208 6 Fourier Series and Integrals with Applications

∞



n=1

[1 − (−1)

]

∞



n=1

(2n − 1)

∞



n=1

(2n − 1)

. (6.10.24)

6.11 Uniform Convergence, Diﬀerentiation, and

Integration

In the preceding section, we have proved the pointwise convergence of the

Fourier series for a piecewise smooth function. Here, we shall consider sev-

eral theorems without proof concerning uniform convergence, term-by-term

diﬀerentiation, and integration of Fourier series.

Theorem 6.11.1. (Uniform and Absolute Convergence Theorem)

Let f (x) be a continuous function with period 2π,andletf

′

(x) be piecewise

continuous in the interval [−π, π]. If, in addition, f (−π)=f (π), then the

Fourier series expansion for f (x) is uniform ly and absolutely convergent.

In the p receding theorem, we have assumed that f (x) is continuous

and f

′

(x) is piecewise continuous. With less stringent conditions on f,the

following theorem can be proved.

Theorem 6.11.2. Let f (x) be piecewise smooth in the interval [−π, π].If

f (x) is periodic with period 2π, then the Fourier series for f converges

uniformly to f in every closed interval containing no discontinuity.

We note that the partial sums s

(x) of a Fourier series cannot approach

the function f (x) uniformly over any interval containing a point of discon-

tinuity of f. The behavior of the deviation of s

(x)fromf (x)insuchan

interval is known as the Gibbs phenomenon. For instance, in the Example

6.7.1, the Fourier series of the function is given by

f (x)=

∞



k=1

sin (2k − 1) x

(2k − 1)

. (6.11.1)

From graphs of the partial sums s

(x) against the x-axis, as shown in

Figures 6.7.2 and 6.7.3, we ﬁnd that s

(x) oscillate above and below the

value of f. It can be observed that, near the discontinuous points x =0

and x = π, s

deviate from the function rather signiﬁcantly. Although

the magnitude of oscillation decreases at all points in the interval for large

n, very near the points of discontinuity the amplitude remains practically

independent of n as n increases. This illustrates the fact that the Fourier

6.11 Uniform Convergence, Diﬀerentiation, and Integration 209

series of a function f does not converge uniformly on any interval which

contains a discontinuity.

Termwise diﬀerentiation of Fourier series is, in general, not permissible.

From Example 6.6.3, the Fourier series for f (x)=x is given by

x =2



sin x −

sin 2x

sin 3x

− ...



, (6.11.2)

which converges for all x, whereas the series aft er formal term-by-term

diﬀerentiation,

1 ∼ 2[cosx − cos 2 x + cos 3x − ...] .

This series is not the Fourier series of f

′

(x) = 1, since the Fourier series of

′

(x) = 1 is the function 1. In fact, this series is not a Fourier series of any

piecewise continuous function deﬁned in [−π, π] as the coeﬃcients do not

tend to zero which contradicts the Riemann–Lebesque lemma.

In fact, the series of f

′

(x) = 1 diverges for all x since the nth term,

cos nx does not tend to zero as n →∞. The diﬃculty arises from the fact

that the given function f (x)=x in [−π,π] when extended periodically

is discontinuous at the points +

π,+3π, .... We shall see below that the

continuity of the periodic fu nction is one of the conditions that must be

met for the termwise d i ﬀerentiation of a Fourier series.

Theorem 6.11.3. (Diﬀerentiation Theorem) Let f (x) be a continuous

function in the interval [−π,π] with f (−π)=f (π),andletf

′

(x) be piece-

wise smooth in that interval. Then Fourier series for f

′

can be obtained

by termwise diﬀerentiation of the series for f, and the diﬀerentiated series

converges pointwise to f

′

at points of continuity and to [f

′

(x)+f

′

(−x)] /2

at discontinuous points.

The termwise integration of Fourier series is possible under more general

conditions than termwise diﬀerentiation. We recall that in calculus, the

series of functions to be integrated must converge uniformly in order to

assure the convergence of a termwise integrated series. However, in the case

of Fourier series, this condition is not necessary.

Theorem 6.11.4. (Integration Theorem) Let f (x) be piecewise contin-

uous in [−π, π], and periodic with period 2π. Then the Fourier series of

f (x)

∞



k=1

cos kx + b

sin kx) ,

whether convergent or not, can be integrated term by term between any

limits.

210 6 Fourier Series and Integrals with Applications

Example 6.11.1. In Example 6.7.2, we have found that f (x)=|sin x| is

represented by the Fourier series

sin x =

∞



k=1

cos (2kx)

(1 − 4k

)

, −π<x<π. (6.11.3)

Since f (x)=|sin x| is continuous in the interval [−π, π]andf (−π)=f (π),

we diﬀerentiate the series term by term, obtaining

cos x = −

∞



k=1

k sin (2kx)

(1 − 4k

)

, (6.11.4)

by use of Theorem 6.11.3, since f

′

(x) is piecewise smooth in [−π, π]. In

this way, we obtain the Fourier sine series expansion of the cosine function

in (−π,π). Note that the reverse process is not permissible.

Example 6.11.2. Consider the function f (x)=x in the interval −π<x≤

π. As shown in Example 6.6.3, the Fourier series of f (x)=x is

x =2



sin x −

sin 2x

sin 3x

− ...



By Theorem 6.11.4, we can integrate the series term by term from a to x

to obtain



− a





−



cos x −

cos 2x

cos 3x

− ...





cos a −

cos 2a

cos 3a

− ...



To determine the sum of the series of constants, we write

= C −

∞



k=1

(−1)

k+1

cos kx

where C is a constant. Since the series on the right is the Fourier series

which converges uniformly, we can integrate the series term by term from

−π to π to obtain



−π

dx =2





−π

Cdx−

∞



k=1

(−1)

k+1



−π

cos kx dx



or,

=2(2πC ) .

Hence,