Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

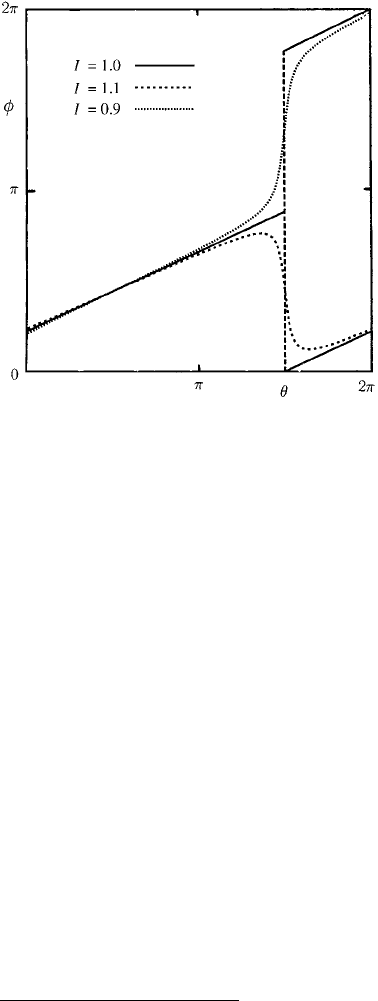
286 9. Perturbed and Coupled Oscillators and Black Holes

Figure 9.6. Change in the phase

resetting curves of the new phase φ as a

function of the old phase θ from (9.11)

forvaluesof0< I < 1, I = 1and

I > 1; note the bifurcation at I = 1.

on this curve is 0, which accounts for the name for this type of resetting curve. Note

also that Type 0 resetting curves cannot be obtained from only a phase stimulus. The

same type of resetting curves, namely, Type 0, is obtained for stimuli I < −1.

Another way of clearly demonstrating the bifurcation from a Type 0 resetting curve

to a Type 1 as I passes through I = 1 is obtained by plotting the new phase φ against

the old phase θ from (9.11). An example of this is shown in Figure 9.6 for representative

values of 0 < I < 1, I = 1andI > 1.

Resetting one’s biological clock as quickly as possible is what everyone wants to

do when suffering from jet lag. What Winfree has unequivocably shown is that circa-

dian rhythms are highly sensitive to light. He has introduced a whole new approach to

the area of internal clocks. With respect to resetting the biological clock, humans are

essentially no different from fruitﬂies and a human’s clock can be reset with the right

light stimulus given at the right time. From Winfree’s (1975) article it is possible to de-

termine when to administer a strong dose of sunlight to yourself to reset your biological

clock after a ﬂight across several time zones.

Winfree (1982, 2000) discusses human

body clocks and the timing of sleep and suggests that their understanding could have

practical medical and psychiatric implications.

9.3 Black Holes

From the analysis in the last section we see that as the stimulus I is increased from 0

there is a distinct bifurcation in phase resetting type as I passes through I = 1. That

For example, going from Seattle to London, there is an eight-hour difference. A good 15-minute dose of

strong sunlight into your eyes around 1

PM should reset your clock. The only problem is getting a dose of

sunlight in England. Going the other way you need to have the strong sunlight around 5

PM in Seattle, where,

of course, there’s the same problem as in England.

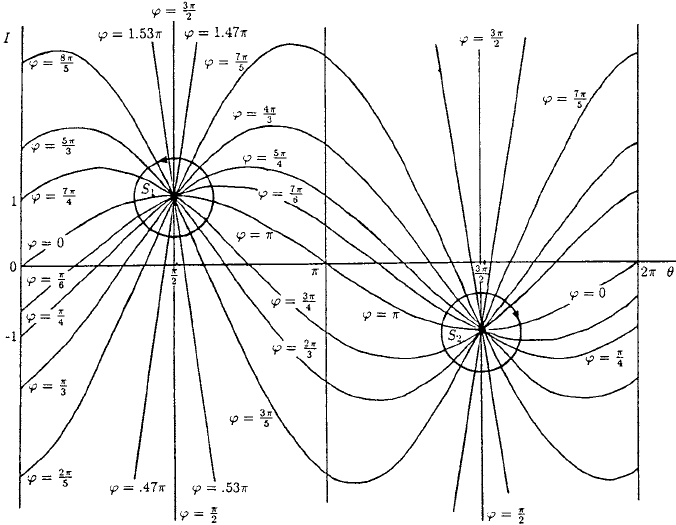
9.3 Black Holes 287

is, there is a singularity in phase resetting for I = 1. To see clearly what is going on

physically we must consider the projection of the φ = φ(θ, I) surface, given by (9.11),

onto the (I,θ)plane for various φ. That is, we construct curves

I = sin θ −cos θ tan φ (9.13)

for various φ in the range 0 ≤ φ ≤ 2π. Although this is an exercise in elementary

curve drawing, using simple calculus, it has to be done with considerable care. The

results are schematically shown in Figure 9.7. Let us ﬁrst consider the old phase range

0 ≤ θ ≤ π and suppose, for the moment, φ = π/2, 3π/2. Irrespective of the value

of φ, all curves pass through the point I = 1,θ= π/2, since there, cos θ tan φ = 0

and I = sin π/2 = 1forallφ. All the curves with π/2 >φ>0, 2π>φ>3π/2

intersect the θ = 0axisatI =−tan φ.Forπ/2 <φ<3π/2 a little calculus on

(9.13) gives the curves shown. The special values φ = π/2, 3π/2 give the vertical

singularity line through θ = π/2, as can be seen by taking the singular limit φ → π/2,

or by simply observing the behaviour of the constant φ phase curves as φ approaches

π/2. Having dealt with the θ -range (0,π)the (π, 2π) range is treated similarly and the

overall picture obtained is shown in Figure 9.7. The important thing to note is that there

Figure 9.7. Projections of the new phase (φ)-old phase (θ)-stimulus (I) surface, given by (9.13), onto the

(I,θ) plane for various φ in the period cycle range 0 ≤ φ ≤ 2π . Note that S

and S

are singularities

into each of which goes a complete selection of phases φ,0≤ φ ≤ 2π; in one case they are traversed

counterclockwise, that is, for S

, and in the other, namely, S

,clockwise.

288 9. Perturbed and Coupled Oscillators and Black Holes

are two singular points S

and S

into each of which goes a constant phase curve of

every phase in (0, 2π); in the one case curves of increasing φ are arranged clockwise

and in the other counterclockwise.

Let us now consider the implications of this important Figure 9.7. Suppose we have

such an oscillator and we give it a stimulus I at a given phase θ. As long as | I | < 1

we can simply read off the new phase given I and the old phase θ ,andwhatismore,

the result is unique. For all | I | > 1, given the old phase θ, once again the new phase is

determined uniquely. In this situation, however, we can get the same new phase φ for a

given I for two different old phases θ . In the former we have, referring to Figure 9.5, a

Type 1 phase resetting while in the latter it is a Type 0 phase resetting.

Now suppose we take the particular stimulus I = 1 and impose it on the oscillator

at phase θ = π/2; the resulting point in Figure 9.7 is the singular point S

, which has no

one speciﬁc phase φ associated with it, but rather the whole range 0 ≤ φ ≤ 2π.Inother

words the effect of this particular stimulus at this speciﬁc phase gives an indeterminate

result. These singular points S

and S

are black holes in the stimulus-phase space, and

are points where the outcome of a stimulus is unknown. If I is not exactly equal to 1,

but close to it, the result is clearly a delicate matter, since all phases φ pass through the

singularity. From a practical point of view the result of such a stimulus on a biological

oscillator is unpredictable. Mathematically, however, if the exact stimulus I = 1isim-

posed at exactly θ = π/2 there is no resultant new phase φ. This is what happens in

the simple pendulum situation when exactly the right impulse is given when the pen-

dulum is just passing through the vertical position. In practice to stop a real pendulum

dead is clearly quite difﬁcult, and even if we could get quite close to the mathematically

calculated conditions, the resulting phase outcome would be far from obvious.

It is clear that the above concepts, due to Winfree (1970; see also 2000), are appli-

cable to any endogenous oscillator, and so the results and implications are quite general.

A key feature then of biological oscillators which can exhibit Type 1 and Type 0 phase

resetting is that there are impulses and phases in their old phase-stimulus space which

correspond to black holes. Perhaps the most important application of this is that there is

thus, for such oscillators, a stimulus, which, if applied at a speciﬁc phase, will annihi-

late the oscillation completely. The continuity argument for the existence of black holes

is that if, as the stimulus is continuously increased, a transition from Type 1 to Type 0

resetting occurs at a speciﬁc value, then a black hole exists at the transition values of

phase and stimulus.

Let us now consider some of the experimental evidence of black holes and annihi-

lation in real oscillators.

9.4 Black Holes in Real Biological Oscillators

There are now several well-documented experimental cases of Type 0 phase resetting

and of annihilation of the basic oscillation by appropriate stimuli at the right phase—all

as predicted above. Other than the cases we discuss in this section, there is, for example,

the Type 0 phase response curve measured in Hydra attenuata by Taddei-Ferretti and

Cordella (1976); the work of Pinsker (1977) on the bursting neurons of Aplysia per-

turbed by synaptic input—again a Type 0 case; and the work of Guttman et al. (1980)

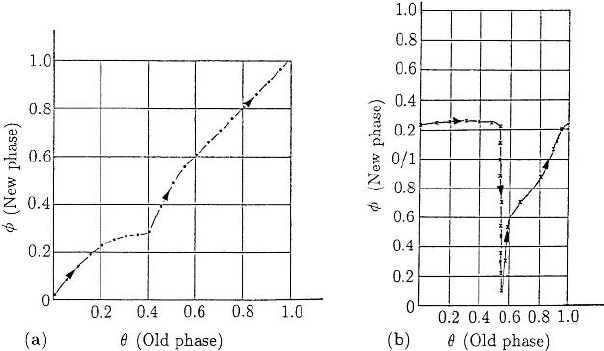
9.4 Black Holes in Real Biological Oscillators 289

which displays annihilation in the squid axon membrane neuron oscillator. Before de-

scribing in detail an experimental case, we give Best’s (1979) direct veriﬁcation of the

existence of black holes in the Hodgkin–Huxley model discussed in Chapter 7, Sec-

tion 7.5, which models the oscillations in the space-clamped membrane of the squid

giant axon.

The Hodgkin and Huxley (1952) model for the space-clamped neuronal ﬁring of

the squid axon given by the equation system (7.37) and (7.38) exhibits limit cycle oscil-

lations. We showed in Section 7.5 that the FitzHugh–Nagumo model of this model had

limit cycle periodic behaviour. Best (1979) numerically investigated the full Hodgkin–

Huxley model (7.37) and (7.38) with an applied current in the range where limit cy-

cle oscillations occurred. He then perturbed the oscillator by subjecting it to voltage

changes (these are the stimuli), with a view to experimental implementation of his re-

sults. He found, as anticipated, Type 1 and Type 0 phase resetting curves; Figure 9.8

shows one example of each.

The existence of a black hole, or null space was indicated in Best’s (1979) simula-

tions by a transition from a Type 1 to Type 0 resetting curve as he increased the voltage

stimulus. This is as we might expect from Figure 9.8, where Figures 9.8(a) and (b) are

topologically different and hence are separated by some bifurcation state. Because of

the approximations inherent in any numerical simulation it is not possible to determine

a single singular point as in Figure 9.7. Instead there is a region around the singularity,

the black holes or null space, where, after a suitable perturbation in an appropriate range

of old phase, the new phase is indeterminate. Figure 9.9 illustrates the results found by

Best (1979). Except for the shaded regions there is a unique reset phase φ,foragiven

old phase θ, and stimulus I; note, however, that there is an (I,θ) subspace where it is

possible to have the same φ for two θs and a single I . Note also that the new phase

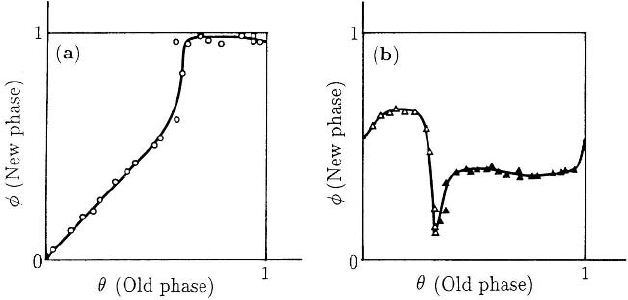
Figure 9.8. (a) Type 1 phase resetting curve obtained for the Hodgkin and Huxley (1952) model when the

endogenous oscillator was subjected to voltage perturbations of 2 mV. The period of the cycle has been

normalised to 1. The average slope across the graph is 1. (b) Type 0 phase resetting curve with voltage

perturbations of 60 mV; here the average gradient is zero. (Redrawn from Best 1979)

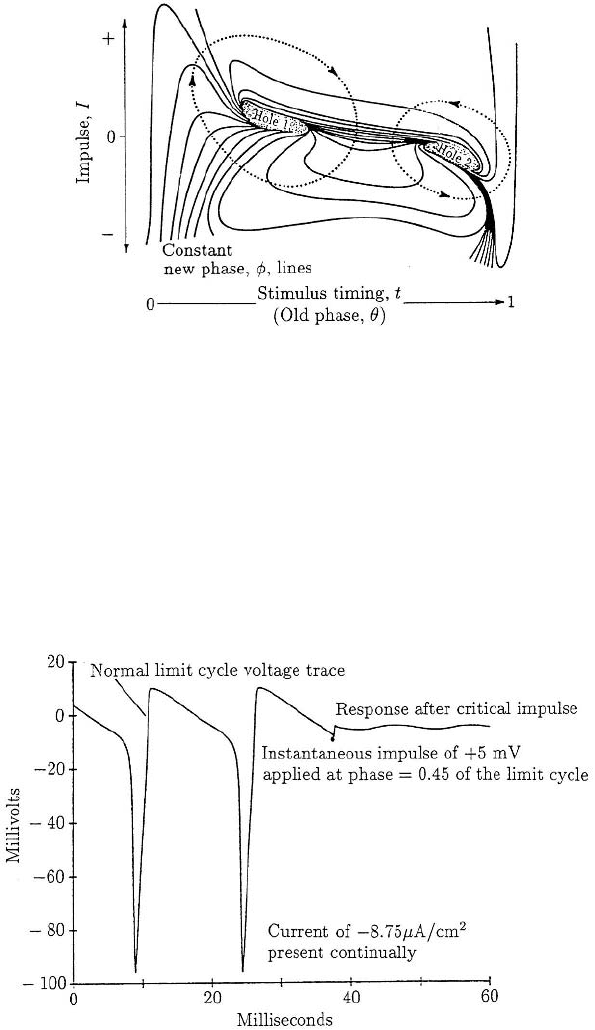
290 9. Perturbed and Coupled Oscillators and Black Holes

Figure 9.9. Black holes or null space (after Winfree 1982) found by Best (1979) for the Hodgkin–Huxley

(1952) model (equations (7.37) and (7.38)) for repetitive ﬁring of the space-clamped giant axon of the squid.

A voltage stimulus and phase which gives a point in the shaded black hole regions produces unpredictable

phase resetting values. A complete path around either of the dashed curves gives a full range of phases.

Figure 9.10. Voltage oscillations in the Hodgkin–Huxley model system (7.37) and (7.38) and the response

when subjected to a critical stimulus (here 5 mV) at 0.45 through the phase, normalised to 1. (After Best

1979). The same applied current was used as in Figures 9.8 and 9.9.

9.4 Black Holes in Real Biological Oscillators 291

values vary through a complete cycle in a clockwise way around Hole 1 and in a coun-

terclockwise way around Hole 2 as indicated in the ﬁgure. A key feature to remember

about stimulus–old phase contour maps like Figure 9.9 is the convergence of contour

lines to a black hole, one for positive stimuli and one for negative stimuli.

Another crucial property of black holes is that if the endogenous oscillator is sub-

jected to a critical stimulus at the appropriate phase the oscillation simply disappears.

Best (1979) demonstrated this with the Hodgkin–Huxley model system; the result is

shown in Figure 9.10. Note the annihilation of the endogenous oscillation. Guttman

et al. (1980) showed experimentally that repetitive ﬁring in space-clamped axons im-

mersed in a weak calcium solution was stopped by a stimulus of the right size applied

at a speciﬁc time in the cycle.

Jalife and Antzelevitch (1979) carried out similar work on the regular periodic beat-

ing of cardiac pacemaker cells, which is, of course, directly related to the cardiac pace-

maker. They used tissue from the hearts of dogs, cats and calves and subjected the basic

oscillation to electrical stimuli. They obtained from their experiments phase resetting

curves which exhibited Type 1 and Type 0 resetting curves; Figure 9.11 shows some of

their results.

From the resetting curves in Figure 9.11 we would expect there to be a transition

value or values for stimulus duration, which destroys the oscillation, namely, in the null

space or black hole of the endogenous cardiac oscillator. This is indeed what was found,

as shown in Figure 9.12(a). Figure 9.12(b) shows the resetting curve with the stimulus

close to the transition value, intermediate between the values in Figures 9.11(a) and (b).

Figure 9.12(c) shows stimulus destruction of the regular oscillation in heart ﬁbres from

a dog.

A.T. Winfree for some years has been investigating the possible causes of sudden

cardiac death and their connections with pacemaker oscillator topology, both temporal

Figure 9.11. Phase resetting curves, normalised and in the notation used above, obtained by Jalife and

Antzelevitch (1979) by applying brief current stimuli to pacemaker cells which spontaneously ﬁre period-

ically. (a) Type 1 resetting, obtained when the stimulus duration was sufﬁciently short, here 10 msec. (b)

Type 0 resetting with a stimulus time of 50 msec. (Photographs courtesy of J. Jalife and reproduced with

permission)

292 9. Perturbed and Coupled Oscillators and Black Holes

Figure 9.12. Experimental results obtained by Jalife and Antzelevitch (1979): (a) The microelectrode traces

of the transmembrane potentials of oscillating cardiac tissue (taken from a kitten) when subjected to a de-

polarising current stimulus of 50 msec duration at successively later times in the cycle. When the time of

stimulus was applied at 130 msec through the cycle, as in trace 3, the oscillation was completely suppressed.

(b) Resetting curve for an intermediate stimulus duration of 30 msec, that is, between those in Figures 9.11(a)

and (b): here the periodic activity of the pacemaker can be destroyed as shown in the third trace in (a). (c)

Oscillation annihilation by a stimulus in heart tissue of the dog. The small extra current stimulus lasts for

200 msec and is applied at progressively later stages in the cycle in 1, 2, 3, 4. In 1 the next ﬁring is slightly

delayed, while in 4 it is advanced. (Photographs courtesy of J. Jalife and reproduced with permission)

9.5 Coupled Oscillators: Motivation and Model System 293

and spatial. Although the contraction of the heart involves a pacemaker, departures from

the norm frequently involve the appearance of circulating contraction waves rather than

the interruption of the ﬁring mechanism. In the case of ﬁbrillation, when the arrhyth-

mias make the heart look a bit like a handful of squirming worms, it may be that a

thorough understanding of the appearance of singular points or black holes could help

to shed some light on this problem. The Scientiﬁc American article by Winfree (1983b)

is speciﬁcally concerned with the topology of sudden cardiac failure. In Chapter 1,

Volume II we discuss spiral rotating waves which have a direct bearing on such heart

problems. The mathematical problems associated with coupled and spatially distributed

oscillators which are subjected to spatially heterogeneous applied stimuli are clearly

challenging and fascinating, and of considerable biological importance.

9.5 Coupled Oscillators: Motivation and Model System

The appearance of biological oscillators and periodic processes in ecology, epidemiol-

ogy, developmental biology and so on is an accepted fact. It is inevitable that in a large

number of situations oscillators are coupled in some way to obtain the required output.

We have just seen how important it is to have some understanding of the effects of per-

turbations on oscillators. So, here we consider some of the effects of oscillator coupling

and describe one of the key analytical techniques used to study such problems. Coupled

limit cycle oscillators have been widely studied mathematically for many years and the

analytical problems are far from trivial. Not surprisingly the range of phenomena which

they can corporately exhibit is very much larger than any single oscillator is capable of

(see, for example, Winfree 2000). The subject is currently one of increasing research

effort, not only in biology but also under the general heading of nonlinear dynamics.

Many of the processes which have been observed are still only partially understood. In

the rest of this chapter we shall mainly be concerned with synchronisation processes

and when they break down. These synchronisation phenomena may be phase locking,

frequency coordination and so on, and they all arise from the interactive coupling of

limit cycle oscillators. Here we restrict our study to the coupling of two oscillators and

consider only weak coupling; we essentially follow the analysis of Neu (1979). Later in

Chapter 12 we consider an important phenomenon associated with a chain of coupled

oscillators when we model the neural arrangement in certain swimming vertebrates.

Before considering the mathematical problem it is relevant to describe brieﬂy one

of the experimental motivations for the speciﬁc model system we study. Marek and

Stuchl (1975) investigated the effect of coupling two Belousov–Zhabotinskii reaction

systems with different parameters, and hence different periodic oscillations. They did

this by having each reaction in a separate stirred tank reactor and coupled them via

an exchange of material between them through a common perforated wall. They ob-

served that if the autonomous oscillators had almost the same frequency then the phase

difference tended to a constant value as time went on: this is known as phase locking.

However, if the difference in the autonomous frequencies was too large then phase lock-

ing did not persist but instead the coupled system had long intervals of slow variation

294 9. Perturbed and Coupled Oscillators and Black Holes

in the phase difference separated by rapid ﬂuctuations over very short intervals. The

analysis we now give will explain these phenomena.

In our analytical study of coupled limit cycle oscillators, it is not necessary to know

in detail the speciﬁc system they model. However, in view of the above experiments, we

have the Belousov reaction system in mind. Suppose that the limit cycle oscillators are

identical and that each, on its own, is governed by the equations

= F(x

, y

= G(x

, y

), i = 1, 2, (9.14)

where the nonlinear functions F and G represent the dynamics of the oscillator. (They

could be, for example, the functions on the right-hand side of (8.27), one of the two-

reactant models for the Belousov reaction discussed in Sections 8.4 and 8.5, or the

interactive dynamics in a predator–prey model such as the one given by (3.18) in Chap-

ter 3, Section 3.3.) We assume that the solutions of (9.14) exhibit a stable limit cycle

behaviour with period T given by

= X (t +ψ

), y

= Y (t + ψ

), i = 1, 2, (9.15)

where here the ψ

are arbitrary constants. So

X(t + ψ

+ T ) = X (t +ψ

), Y (t + ψ

+ T ) = Y (t + ψ

), i = 1, 2.

So as to formulate the weak coupling in a convenient (as we shall see) yet still

general way we consider the nondimensional model system

= F(x

, y

) +ε{k(x

− x

) + λ f (x

, y

)},

= G(x

, y

) +ε{k(y

− y

) + λg(x

, y

)},

= F(x

, y

) +εk(x

− x

= G(x

, y

) +εk(y

− y

(9.16)

where 0 <ε 1andk > 0 is a coupling constant. When ε = 0 the oscillators are

uncoupled and these equations reduce to (9.14). The generality in the form (9.16) comes

from the λ-terms. If ε = 0andλ = 0 the two oscillators are identical with uncoupled

solutions like (9.15). If ε = 0andλ = 0, two different oscillators are coupled, with the

ελ-terms in the ﬁrst two equations of (9.16) simply part of the isolated limit cycle oscil-

lator given by these two equations. The speciﬁc coupling we have chosen, represented

by the k-terms, is proportional to the differences x

− x

and y

− y

. In the case of

Marek and Stuchl’s (1975) experiments, this reﬂects the fact that there is a mass transfer.

In the case of interacting populations it can be thought of as a mass transfer of species,

a kind of diffusion ﬂux approximation. In fact, when considering interhabitat inﬂuence

on the population dynamics, it is often incorporated in this way: it takes gross spatial

9.6 Oscillation Phase Locking: Fireﬂy Synchronisation 295

effects into account without diffusion terms as such, which of course would make the

models partial differential equation systems; these we consider later.

9.6 Phase Locking of Oscillations: Synchronisation in Fireﬂies

When biological oscillators are coupled they can give rise to an astonishingly rich ar-

ray of phenomena such as rhythm splitting, phase locking and entrainment and so on.

The mathematics of coupled oscillators is challenging and can be highly complex and

involved. There is a vast literature on the subject ranging from the very abstract to the

very practical, such as synchrony in running and human sleep–wake cycles (Strogatz

1986). The beautiful (both scientiﬁcally and visually) book on biological clocks by

Winfree (1987) discusses biological clocks in a wide variety of ﬁelds with an emphasis

on circadian rhythms and phase resetting; see also the book When Time Breaks Down

(Winfree 1987) which deals primarily with cardiac rhythms. The introductory book by

Glass and Mackey (1988) has many examples of rhythmic phenomena associated with

biological clocks; the applications are mainly in physiology. The nontechnical Scientiﬁc

American article by Strogatz and Stewart (1993) describes a variety of interesting syn-

chronisation phenomena which includes a remarkable photograph of ﬁreﬂies ﬂashing in

synchrony; this is a topic we discuss below.

An interesting, practical example, where the mathematics and the biology are inti-

mately related, was studied by Glass and his colleagues (Guevara et al. 1981, Guevara

and Glass 1982, Keener and Glass 1984). The model is closely related to the one we

discuss below but theirs gives rise to a nonlinear difference equation of the type we dis-

cussed in Chapter 2. They denote by φ

the phase just before a delta function stimulus

is given to the system; that is, φ

is the old phase. Then the new phase, here denoted by

i+1

in a discrete model, is given by

i+1

= g(φ

) +2πτ(mod2π),

where g is a function of φ

, a function that was subsequently determined by experiment

on a speciﬁc system, and τ is the normalised stimulus period relative to the cycle length.

Stable steady states of this equation correspond to phase locking; the preliminary anal-

ysis is like that in Chapter 2. Guevera and Glass (1982) used this equation to study

the entrainment of the basic equation (9.4) above subjected to a periodic delta func-

tion stimulus. For a range of parameters they also found chaotic behaviour. Even such

simple looking equations can give rise, as we have seen, to a plethora of complex and

unexpected solutions. What is particularly interesting about this work is that subsequent

to the analysis Guevara et al. (1981) actually measured resetting curves experimentally

in a preparation of spontaneously beating embryonic heart cells. Over a wide range of

amplitudes and frequencies they were able to predict the rhythms observed, including

phase locked and chaotic rhythms. This is an excellent example of how the mathemat-

ical modelling and analysis helped to further our understanding of an important and

complex biological phenomenon.

There seems no end to the modelling challenges associated with coupled oscillators

in the biomedical sciences. Here we only touch on the subject. Below we discuss in