Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

296 9. Perturbed and Coupled Oscillators and Black Holes

a little more detail a particularly well-known biological example. In Sections 9.7 to

9.9 we discuss the weak coupling of two oscillators which we analyse using singular

perturbation techniques. Another example, involving many oscillators, is discussed later

in Chapter 12.

A striking and well-known visual example of coupled biological oscillators is the

phase-locking synchrony of the periodic ﬂashing of light by large groups of stationary

ﬁreﬂies (Pteroptyx malaccae). It is the males that ﬂash to attract the females who ﬂy

around looking for males with a particularly attractive ﬂash. Many experimental studies

have quantiﬁed the ability of the individual ﬁreﬂy (and other insects) to vary the peri-

odicity of the light ﬂashes. The Scientiﬁc American article by Buck and Buck (1976)

is a very nice introduction to the subject of ﬁreﬂy synchrony. Buck (1988) reviews

the biological literature on the synchronous rhythmic ﬂashing of these ﬁreﬂies. Early

work by Hanson (1978) showed that an individual ﬁreﬂy could change the phase of its

light-emitting oscillator, which is controlled by an endogenous neural pacemaker, and

synchronise, or entrain, to a ﬂashing light as long as its period was in the neighbour-

hood of the ﬁreﬂy’s natural period of about 0.9 second. If the period of the artiﬁcial

light stimulus was too far away from the natural period no entrainment was possible.

Some ﬁreﬂies are better at entrainment than others; Pteroptyx malaccae seem to be the

masters, being able to change their frequency by almost 15%. There have been several

mathematical models of synchronous ﬁreﬂies notably by Rinzel and Ermentrout (1983),

Ermentrout (1991) and Mirollo and Strogatz (1990). Here we discuss only the simple,

but effective, model of Rinzel and Ermentrout (1983).

As in Section 9.1 let us denote the phase of the ﬁreﬂy’s oscillator at time t by θ(t)

and let its natural frequency be ω. That is, in the absence of any external stimulus, the

phase satisﬁes

dθ

= ω. (9.17)

To be speciﬁc, we assume the oscillator ﬁres, and the light ﬂashes, at θ = 0. Let us

denote the external phase by θ

(t), which has a frequency ω

andsosatisﬁes

dθ

= ω

. (9.18)

The ﬁreﬂy tries to synchronise its frequency to that of the external stimulus, speeding

up if it is too slow and slowing down if it is too fast. A simple model which does this is

dθ

= ω + I sin (θ

−θ), (9.19)

where the parameter I > 0. The size of the stimulus, I, is a measure of how effective

the ﬁreﬂy is at changing its frequency. If θ

is ahead of θ(0 <ω

−ω<π)then

θ>ω

and the ﬁreﬂy tries to speed up its phase. If

θ<ωthe ﬁreﬂy tries to slow down. This

form (9.19) is a special case of the equation for phase resetting, equation (9.5). A similar

type of assumption, based on a function of θ −θ

(t) but in a more complex situation, is

used below in Chapter 12, Section 12.3.

9.6 Oscillation Phase Locking: Fireﬂy Synchronisation 297

When our interest is in determining when synchrony will occur it is informative, as

we show below and particularly in Chapter 12, Section 12.3, to consider the equation

for the difference, φ, in phases; that is, φ = θ −θ

. From (9.18) and (9.19) we have

dφ

dθ

−

dθ

= ω

−ω − I sin φ, φ(t) = θ

(t) −θ(t). (9.20)

If we introduce new variables

τ = It,δ=

(ω

−ω)

(9.21)

the equation for φ becomes



dφ

dτ

= δ −sin φ. (9.22)

The dimensionless parameter δ has a deﬁnite physical interpretation: it is a measure of

the difference between the external frequency and the natural one to the strength of the

stimulus, I . As we saw in Sections 9.2 and 9.3, the size of I is critical.

We are interested in the steady state solutions of (9.22) and their stability. If we

have a stable steady state solution, φ

> 0 say, this means, from (9.20), that the external

stimulus phase, θ

, is always ahead of the ﬁreﬂy phase, θ, by a constant amount. The

ﬁreﬂy’s oscillator is therefore phase locked to the stimulus but it ﬂashes just after it. If

δ = 0, φ = 0 is a solution of (9.22) and in this case, if φ = 0 is stable, the oscillators

ﬂash with zero phase difference and so are in unison. The question of entrainment hinges

on the steady states of (9.22) and their stability.

In Chapter 1 we saw that all we had to do was, in effect, graph the right-hand side of

(9.22), read off the steady states and note whether the gradient was positive or negative.

Figure 9.13 illustrates the main solution possibilities for δ ≥ 0.

The stability of the steady states is determined by the gradient at the steady state—

stable if the gradient is negative and unstable if the gradient is positive. With this model

there is only one stable steady state, when the ﬁreﬂy and stimulus are phase locked, if

−1 <δ<1. The situation −1 <δ<0 is similar to that in Figure 9.13 but with

δ<0.

In Figure 9.13(b), the stable steady state is 0 <φ

<πandsotheﬁreﬂymust

increase its frequency to phase lock. If δ>δ

= 1, as in Figure 9.13(c), it simply

cannot keep up and the phase difference φ simply increases until the cycle starts over

again when φ reaches 2π. This latter case is phase drift.Sinceφ



> 0 in Figure 9.13(c)

and is not constant, this implies that the phase drift increases but at a nonuniform rate.

This is in keeping with the experimental results of Hanson (1978).

We can make several predictions with this model, the nonuniform phase drift if

δ>1 is just one. The key prediction is that phase locking by the stimulus is possible if

the external frequency, ω

satisﬁes

ω − I ≤ ω

≤ ω + I (9.23)

298 9. Perturbed and Coupled Oscillators and Black Holes

(c)

(a)

(b)

−π



δ = 0

δ>0

δ>δ

δ = δ

= 1

Figure 9.13. Steady state solutions of the phase difference equation (9.22) for various δ.Ifδ<δ

(= 1) two

solutions exist, while if δ>δ

no steady state solutions exist.

which gives the range of the stimulus frequency for entrainment. Just as above, the

stimulus intensity I is important. If we know, from experiment, the range of stimulus

frequency, we can calculate I and then predict the phase locked phase difference from

(9.20) and (9.22) as

= θ

−θ

= sin

−1



−ω



, −

≤ φ

≤

. (9.24)

When −1 ≤ δ ≤ 1, the dimensional period, T , of the phase locked ﬁreﬂy oscillator is

obtained from (9.22) as the time for φ to change by 2π; namely,

T =



dτ =



2π

dφ

dφ/dτ



2π

dφ

δ − sin φ

which gives the entrained period as

9.7 Singular Perturbation Analysis: Preliminary Transformation 299

T =

2π

I (δ

−1)

1/2

2π

(ω

−ω)

− I

1/2

. (9.25)

As δ →±1, the period becomes inﬁnitely large; in other words there is no entrain-

ment as, of course, is indicated in Figure 9.13(c). We can now see how ﬁreﬂies can

synchronise their periodic pulsing of light: as one ﬁreﬂy, for example, with a stronger

I, entrains another, the group stimulus with a single frequency grows until all are en-

trained. A stronger I implies a smaller δ and hence a small difference in frequency

between the ‘pacemaker’ and those with frequencies near it. If the whole group now

ﬂashes with the same frequency it must be somewhat difﬁcult for a circling female to

light on the leader!

The ﬁreﬂy Pteroptyx malaccae is not the only species of ﬁreﬂy, but it seems to be

the most ﬂexible in being able to phase lock onto an external stimulus. Now that we

have seen how a simple model can capture some of the experimental results, we should

examine models which reﬂect more of the biology. The assumption that adaptation is

governed by a sine function as in (9.19) is too simple. In Chapter 12 we again use such

an assumption when dealing with N oscillators. A more appropriate inﬂuence equation

would be, in place of (9.19),

dφ

= ω + h(φ), (9.26)

where h(φ) is a periodic function of its argument but not necessarily symmetric. A

more sophisticated model which incorporates more of the adaptive features of the ﬁreﬂy

Pteroptyx malaccae and which uses a more general inﬂuence function, as in the last

equation, is given by Ermentrout (1991). He also numerically simulates how a group

of ﬁreﬂies approach synchrony in a ﬁreﬂy tree. The above model shows synchrony but,

except for δ = 0, with a permanent phase lag. This is a drawback as a model for a ﬁreﬂy

tree where there is synchrony with almost no phase lag. This aspect is also discussed,

and a possible mechanism for effecting this, by Ermentrout (1991).

9.7 Singular Perturbation Analysis: Preliminary Transformation

Equations (9.16) in general are hard to analyse. Even numerically it is not easy to see

how the solution behaviour depends on the various parameters, particularly in the non-

identical autonomous oscillator case. Since in many situations of interest the coupling

is weak, and as we anticipate this to be the case in many biological applications, we

exploit the fact that 0 <ε 1 and use singular perturbation theory (see, for example,

Murray 1984 for a short pedagogical discussion of the basic techniques).

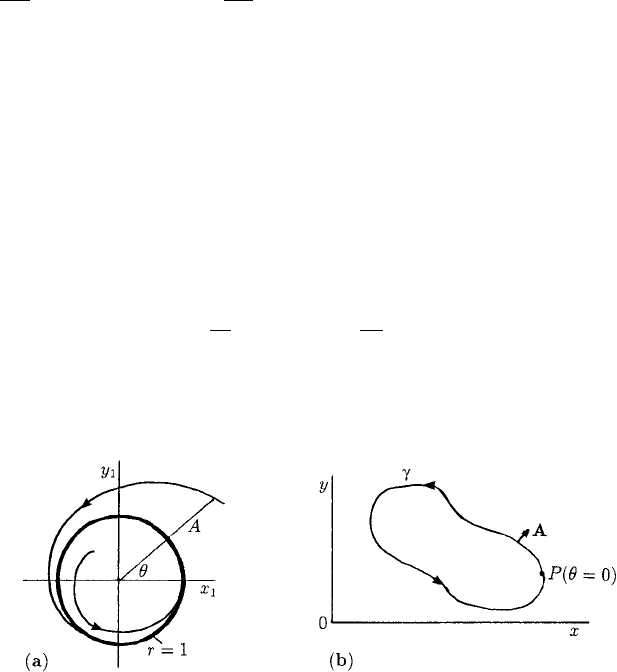
Each oscillator has its own limit cycle solution which can be represented by a closed

trajectory γ in the x − y phase plane. We can introduce a new coordinate system using

this curve as the basis of the local coordinate system. We can characterise the periodic

limit cycle by a phase θ which goes from 0 to T as we make a complete circuit round

γ and any perturbation from it by the perpendicular distance A measured from γ ;onγ ,

A = 0. It turns out to be particularly convenient algebraically to use this characterisation

300 9. Perturbed and Coupled Oscillators and Black Holes

in our coupled oscillator analysis. So in place of (9.15) as our autonomous limit cycle

solutions we have

= X (θ

), y

= Y (θ

), i = 1, 2, (9.27)

where X(θ

) and Y (θ

) are T -periodic functions of θ

. Note that θ

and t are related by

dθ

/dt = 1.

The idea of representing the solution of a phase plane system, which admits a pe-

riodic limit cycle solution, in terms of the phase and a perturbation perpendicular to

the limit cycle can be illustrated by the following example, which, although admittedly

contrived, is still instructive.

Consider the differential equation system

= x

(1 −r) −ωy

= y

(1 −r) +ωx

, r = (x

+ y

)

1/2

, (9.28)

where ω is a positive constant. A phase plane analysis (see Appendix A) shows that

(0, 0) is the only singular point and it is an unstable spiral, spiralling anticlockwise. A

conﬁned set can be found (just take r large and note that on this large circle the vec-

tor of the trajectories (dx

/dt, dy

/dt) points inwards), so by the Poincar

e–Bendixson

theorem a limit cycle periodic solution exists and is represented by a closed orbit γ ,in

the (x

, y

) plane. If we now change to polar coordinates (r,θ)with

= r cos θ, y

= r sin θ (9.29)

the system (9.28) becomes

= r(1 −r),

dθ

= ω. (9.30)

The limit cycle, the trajectory γ , is then seen to be r = 1. The solution is illus-

trated in Figure 9.14(a). The limit cycle is asymptotically stable since from (9.30) any

Figure 9.14. (a) The phase plane solution of the differential equation system (9.30) the asymptotically stable

limit cycle is r = 1 with the phase θ = ωt,ontakingθ = 0att = 0. (b) Schematic example illustrating the

local limit cycle coordinates. The point P has phase θ = 0 and the phase increases by 2π on returning to P

after moving round γ once.

9.7 Singular Perturbation Analysis: Preliminary Transformation 301

perturbation from r = 1 will die out with r simply winding back onto r = 1, in an

anticlockwise way because dθ/dt > 0. In this example if the perturbation from the

limit cycle is to a point r < 1 then, from (9.30), r increases while if the perturbation

is to a point r > 1, r decreases as it tends to the orbit r = 1. In this case r = 1isthe

equivalent of the orbit γ and A, the perpendicular distance from it is simply r − 1. The

differential equation system in terms of A(= r −1) and θ is, from (9.30),

=−A(1 + A),

dθ

= ω. (9.31)

We can, of course, integrate (9.30) exactly to get

r(t) =

(1 −r

) +r

,θ(t) = ωt +θ

, (9.32)

where r(0) = r

, θ(0) = θ

and from (9.29),

(t) = r(t) cos θ(t), y

(t) = r(t) sin θ(t). (9.33)

As t →∞, r(t) → 1(soA(t) → 0) and x

→ cos θ, y

→ sin θ, which are the

equivalent of the X(θ) and Y (θ) in (9.27): they are 2π−periodic functions of θ .Here

therateoftraversingγ (that is, r = 1) is dθ/dt = ω from (9.31). Figure 9.14(b)

schematically illustrates the general situation. There θ = 0 is taken to be at some point

P and the phase increases by 2π as the orbit γ is traversed once in an anticlockwise

sense.

If we now consider our two oscillators, each with its autonomous closed limit cycle

orbit γ

, i = 1, 2, the effect of coupling will be to alter the orbits and phase of each. We

can characterise the effect in local coordinate terms by a phase θ

which parametrizes

points on γ

and a perturbation A

perpendicular to the original limit cycle orbit. Recall

that for the coupled oscillator system (9.16) we are interested in weak coupling and so

0 <ε 1. With ε = 0 each oscillator has its limit cycle solution which in terms of the

phase we can write as in (9.27); namely,

= X (θ

), y

= Y (θ

), i = 1, 2. (9.34)

= t +ψ

⇒

dθ

= 1. (9.35)

We expect that the effect of the O(ε) coupling is to cause the orbits γ

, given by (9.27),

to be displaced by O(ε). We can thus see that an appropriate change of variables is from

, y

) for i = 1, 2 to the local variables A

and the new phase θ

for i = 1, 2, where

is the distance perpendicular to the orbit γ

To motivate the speciﬁc variable transformation we shall use, refer now to Fig-

ure 9.15. In the absence of coupling, the trajectory γ is traversed with velocity (dx/dt,

dy/dt) parallel to γ . In terms of the phase θ, which increases monotonically as the

orbit is traversed, the velocity from (9.34) and (9.35) is equal to (X



(θ), Y



(θ)) where

primes denote differentiation with respect to θ. This velocity vector is perturbed, due to

302 9. Perturbed and Coupled Oscillators and Black Holes

Figure 9.15. Schematic visualization of the effect of coupling on the limit cycle orbit γ . The perpendicular

displacement A of the velocity vector is given by the appropriate vector product; namely, A(X



, Y



, 0) ×

(0, 0, 1),thatis,A(Y



, −X



, 0).

the coupling, and the orbit γ will be displaced. This displacement can be described at

each point by the perpendicular distance it is displaced, denoted by the vector A in the

ﬁgure. Since A is the vector product of the velocity (X



(θ), Y



(θ), 0) and the unit vector

perpendicular to the (x, y) plane, that is, (0, 0, 1),thisgives

A = A(X



(θ), Y



(θ), 0) ×(0, 0, 1) = (AY



(θ), −AX



(θ), 0). (9.36)

Now consider the system (9.16) with 0 <ε 1 with our assumption that the

autonomous orbits are perturbed O(ε). An appropriate change of variable from (x

, y

)

to (A

,θ

) is then, using (9.34) and (9.36),

= X (θ

) + ε A



(θ

), y

= Y (θ

) −ε A



(θ

), i = 1, 2. (9.37)

Here we have used ε A in place of A to emphasise the fact that since ε is small in our

analysis, so is the orbit perturbation.

9.8 Singular Perturbation Analysis: Transformed System

Let us now use the change of variable (9.37) in the coupled system (9.16) with 0 <

ε  1. That is, we use (9.37) in the right-hand sides and expand in a Taylor series in

ε: the algebra is complicated and tedious, but the concise, interesting and important end

result is worth it, not just for the results we exhibit in this chapter but also for two other

dramatic phenomena we shall discuss in Chapters 12 and 13. We carry out enough of

the algebra to show how to get the equations (9.16) in terms of the variables θ

and A

;

however, use of separate pen and paper is recommended for those who want to follow

the details of the algebra. (Those readers who wish to skip this algebra can proceed

to equations (9.45) although later reference will be made to some of the deﬁnitions

included here.)

In the following, the argument of the various functions, mainly X and Y ,isθ

unless

otherwise stated or included for emphasis. The ﬁrst of (9.16), using (9.37), becomes

9.8 Singular Perturbation Analysis: Transformed System 303

= X



dθ

+εY



+ε A



dθ

= F(X, Y ) + ε A



(X, Y ) − X



(X, Y )]+εk[X(θ

) − X(θ

)]

+ελf (X, Y ) + ε

k[A



(θ

) − A



(θ

)]

+ε

λA



(X, Y ) − X



(X, Y )]+O(ε

(9.38)

while the second becomes

= Y



dθ

−εX



−ε A



dθ

= G(X, Y ) + ε A



(X, Y ) − X



(X, Y )]+εk[Y(θ

) − Y (θ

)]

+ελg(X, Y ) + ε

k[A



(θ

) − A



(θ

)]

+ε

λA



(X, Y ) − X



(X, Y )]+O(ε

(9.39)

When ε = 0 we have from (9.14) and (9.34),



(θ

) = F(X, Y ), Y



(θ

) = G(X, Y ). (9.40)

Now multiply (9.38) by X



(θ

) and add to it Y



(θ

) times (9.39) to get

2

)

dθ

+ε A





−Y





)

dθ

=[X



F(X, Y ) +Y



G(X, Y )]+ε A



(X, Y ) − G

(X, Y )]

− X

2

(X, Y ) + Y

2

(X, Y )}+εk{X



[X(θ

) − X (θ

)]



[Y (θ

) −Y (θ

)]}+ ε



(θ



(θ

)

− X



(θ



(θ

)]+ελ[X



f (X, Y ) +Y



g(X, Y )]

+ε

λA



(X, Y ) − g

(X, Y )]−X

2

(X, Y )

2

(X, Y )}+O(ε

From (9.40), X



F(X, Y ) = X

2

and Y



G(X, Y ) = Y

2

so the last equation becomes

(1 +εΓ A

)

dθ

= R

+ε[R

Ω A

+ R

kr + R

kV + R

γλ]+O(ε

where R

= X

2

= 0and

Γ = X





−Y





γ = X



f (X, Y ) +Y



g(X, Y ), R

r =−XX



−YY



Ω = X



(X, Y ) − G

(X, Y )]−X

2

(X, Y ) + Y

2

(X, Y ),

V = X



(θ

)X(θ

) + Y



(θ

)Y (θ

(9.41)

304 9. Perturbed and Coupled Oscillators and Black Holes

If we now divide both sides by R

(1+εΓ A

) and expand the right-hand side as a series

for 0 <ε 1, we get

dθ

= 1 +ε[{Ω(θ

) −Γ(θ

)}A

+λγ (θ

) +kr(θ

) +kV(θ

,θ

)]+O(ε

(9.42)

In a similar way we get the equation for A

by multiplying (9.38) by Y



(θ

) and

subtracting from it, X



(θ

) times (9.39). Using (9.40) and (9.42) for dθ

/dt, remember-

ing that ε  1, we get

= Φ(θ

+kU(θ

,θ

) + λφ(θ

) +εΨ (A,θ

θ) + O(ε

), (9.43)

where

U(θ

,θ

) = X (θ



(θ

) −Y (θ



(θ

) (9.44)

and Φ, φ and Ψ are all determined: A and θ

θ are the vectors (A

, A

) and (θ

,θ

).The

only functions whose exact form we require are U(θ

,θ

) and V(θ

,θ

), given by (9.44)

and (9.41) respectively.

If we now do the same with the 3rd and 4th equations of (9.16) we ﬁnd that the

effect of the transformation to the (A

,θ

) dependent variables is to replace the model

coupled oscillator system (9.16) by

= Φ(θ

+kU(θ

,θ

) +λφ(θ

) +εΨ

(A,θ

θ) + O(ε

dθ

= 1 +ε[{Ω(θ

) −Γ(θ

)}A

+λγ (θ

) +kr(θ

) +kV(θ

,θ

)]+O(ε

)

(9.45)

= Φ(θ

+kU(θ

,θ

) + εΨ

(A,θ

θ) + O(ε

)

dθ

= 1 +ε[{Ω(θ

) − Γ(θ

)}A

+kr(θ

) +kV(θ

,θ

)]+O(ε

(9.46)

The functions V and U, given by (9.41) and (9.44), will be referred to later. The exact

forms of the functions Φ, φ, Γ , γ , Ω, Ψ

, Ψ

and r are not essential for the following

analysis, but what is important is that all of them are T -periodic in θ

and θ

and that Φ

satisﬁes the relation



Φ(σ)dσ<0. (9.47)

This last relation comes from the fact that the original limit cycle solutions of the un-

coupled oscillators are stable; we digress brieﬂy to prove this.

9.9 Singular Perturbation Analysis: Two-Time Expansion 305

Limit Cycle Stability Condition for the Uncoupled Oscillators

The oscillators are uncoupled when k and λ are zero. We want to keep ε = 0sincewe

are going to study the perturbed limit cycle oscillator using the transformation (9.37).

In terms of the variables A and θ the governing system from (9.45) and (9.46), with

k = λ = 0isthen

= Φ(θ)A + O(ε),

dθ

= 1 + O(ε), (9.48)

where Φ is a T -periodic function of θ. For times O(1) the second equation gives θ ≈ t

and the ﬁrst becomes

= Φ(t)A + O(ε),

which on integrating from t to t + T gives

A(t + T )

A(t)

=[1 + O(ε)]exp





t+T

Φ(σ)dσ



=[1 + O(ε)]exp





Φ(σ)dσ



(9.49)

where the limits of integration have been changed because Φ is a T -periodic function.

The unperturbed limit cycle is A ≡ 0, θ = t + ψ. So, the limit cycle is stable if all the

solutions of (9.48) have A(t) → 0ast →∞. From (9.49) we see that if



Φ(σ)dσ<0

then A(t + T )<A(t) for all t and so A(t) → 0ast →∞.

9.9 Singular Perturbation Analysis: Two-Time Expansion

The O(ε) terms in the equations (9.45) and (9.46) will have an effect after a long time,

O(1/ε) in fact. This suggests looking for an asymptotic solution as ε → 0fortheA

and θ

in (9.45) and (9.46) in the following form,

∼

+ε

,θ

∼

+ε

, (9.50)

where the Asandθ s are functions of the time t, the fast time, and τ = εt, the long

or slow time. In other words only after times τ = O(1),thatis,t = O(1/ε),dothe

ε-effects show. (See, for example, Murray 1984 for an elementary exposition to this

two-time expansion procedure.) Now all time derivatives

∂

∂t



dτ



∂

∂τ

∂

∂t

+ε

∂

∂t

, (9.51)