Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

276 8. BZ Oscillating Reactions

Table 8.1. Comparison of values obtained from the relaxation oscillator approximation (8.26) for the BZ

reaction with observed values. (From Field et al. 1972)

Calculated Values Experimental Values

Period 183–228 s 110 s

[Br

−

]

=[Br

−

]

crit

1.7 ×10

−5

[BrO

−

] 2 × 10

−5

[BrO

−

]

[Br

−

]

=[Br

−

]

jumpup

0.3 [Br

−

]

crit

0.3 [Br

−

]

crit

[Br

−

]

=[Br

−

]

max

1.6 ×10

−3

[BrO

−

]=90 [Br

−

]

crit

3 [Br

−

]

crit

by (8.42) with (8.43), followed by a rapid increase in [Br

−

] to its value at A again. Thus

the relaxation oscillator approximation (8.26) mimics the real experimental oscillator of

Figure 8.1. To go further we must compare actual measurable quantities.

The experimentally suggested value for f from Field and Noyes (1974) is f =

0.5. Taking the limit f → 0.5 in (8.39), by setting f = 0.5 + ω and then letting

ω → 0, T

= 2ln(2) − 1. Because of the smallness of q the major part of the

period comes from T

. Now take the values in (8.4), which also gives y

used in the

nondimensionalisation of the bromide ion concentration y, and substitute them into the

limiting values for y

y(=[Br

−

]) from (8.31), and in the expressions for the T

bounds

and T

from (8.38) and (8.39); Table 8.1 lists the values obtained. The table also gives

the experimentally observed values of Field et al. (1972). Considering the complexity

of the reaction and the number of approximations used in reducing the mechanism to

manageable proportions and ﬁnally to the relaxation oscillator model, the results are

very good.

When the parameter f is in the ranges which give null clines typically as in Fig-

ures 8.4(b) and (c), oscillations are not possible for the mechanism (8.26) as we saw

in Chapter 7, Section 7.3. However the mechanism in these cases can exhibit threshold

behaviour; compare with Figures 7.5(a) and (b). Further, if reversibility is allowed in

the basic FKN model mechanism (8.2) it is possible to have three positive steady states

of which two are stable, as in Figure 7.4(d). This corresponds to the biological switch

behaviour also discussed in Chapter 7, Section 7.3 and schematically illustrated in Fig-

ure 7.5(c). Numerical studies of the reversible model also indicate bursting behaviour

and chaos. Various plausible models for the Belousov–Zhabotinskii reaction have pre-

dicted a variety of unexpected phenomena which should be experimentally exhibited by

the real reaction, and many have now been conﬁrmed; see, for example, Tyson (1985),

Field and Burger (1985) and Scott (1991). Barkley et al. (1987) demonstrated the exis-

tence of quite complex behaviour including periodic bursting, hysteresis and periodic-

chaotic sequences. Gy

orgyi and Field (1991) presented some models for the BZ reaction

which demonstrate deterministic chaos.

Here we have considered only homogeneous or well-stirred systems. When we

investigate, in later chapters, coupled biological oscillators and unstirred systems, where

diffusion effects must be included, a new and astonishing range of phenomena appear.

Once again the Belousov–Zhabotinskii reaction is the key reaction used in experiments

to verify the theoretical results.

Exercises 277

Exercises

1 Another scaling (Murray 1977) of the FKN model results in the third-order system

= y − xy + x(1 −qx),

=−y − xy +2 fz,

= δ(x − z),

where ε and q are small. Determine the steady states, discuss their linear stability

and show that a conﬁned set for the positive steady state is

1 < x <

2 fq

1 + q

< y <

, 1 < z <

2 With the system in Exercise 1, derive the relevant reduced second-order system on

the basis that 0 <ε 1. Sketch the null clines in the phase plane, exploiting the

fact that 0 < q  1, and hence determine the necessary conditions on f for a limit

cycle solution to exist.

3 A relaxation oscillator is given by

= f (x) − y,

= x, f (x) = x −

where 0 <ε 1. Sketch the limit cycle trajectory in the y, x phase plane, noting

the direction of motion. Determine the period T to O(1) as ε → 0.

Approximate the function f (x) by a piecewise linear function, and sketch

the corresponding phase plane limit cycle. Integrate the equations using the piece-

wise linear approximation. Hence, sketch the solution x as a function of t.Also

evaluate the O(1) period and compare the result with that in the ﬁrst part of the

question.

4 A possible relaxation oscillator model for the FKN mechanism is governed by the

dimensionless system

2 fz(q − x)

x +q

+ x(1 −x),

= x − z,

where 0 <ε 1, 0 < q  1and f = O(1). Using the results in Exercise 2, when a

limit cycle solution is possible, sketch the relaxation oscillator trajectory, determine

the maximum and minimum values for x and z, and obtain expressions for the O(1)

estimate for the limit cycle period.

9. Perturbed and Coupled Oscillators and

Black Holes

9.1 Phase Resetting in Oscillators

With the plethora of known biological oscillators, and their generally accepted impor-

tance, it is natural to ask what effects external perturbations can have on the subsequent

oscillations. In his pioneering work on circadian rhythms in the 1960’s, A.T. Winfree

asked this basic and deceptively simple question in a biological context in connec-

tion with his experimental work on the periodic emergence of the fruit ﬂy, Drosophila

melanogaster, from their pupae. Since then a series of spectacular discoveries of hitherto

unknown properties of perturbed oscillators, spatially coupled oscillators, oscillators

coupled to diffusion processes and so on (see, for example, Chapter 12 and Chapter 1,

Volume II), have been made as a result of this simple yet profound question. Winfree

has developed a new conceptual geometric theory of biological time, which poses many

challenging and interesting mathematical problems. Winfree’s (2000) seminal book,

which has a full bibliography, discusses the area in detail. He also gives numerous im-

portant examples of biological situations where a knowledge of such effects is crucial

to understanding certain phenomena which are observed.

The periodic pacemaker in the heart is an important oscillator and one which is

being widely studied, in particular the effects of imposed perturbations. For example,

Jalife and Antzelevitch (1979), whose results we discuss in Section 9.4, deal with pace-

maker activity in cardiac tissue; Krinsky (1978) discusses cardiac wave arrhythmias;

Winfree (1983a,b) discusses, among other things, the topological aspects of sudden

cardiac death. There is also interesting work on the sophisticated neural control of syn-

chrony of breathing to stride in runners and horses (see, for example, Hoppensteadt

1985 and the references there).

We saw in Section 7.5 above that under certain conditions nerve cells can exhibit

regular periodic ﬁring. In view of the crucial importance of neuronal signalling it is

clearly of considerable interest to study the effect of external stimuli on such oscilla-

tions. The work of Best (1979) is of particular relevance to this and the following three

sections. He subjected one of the accepted models for the propagation of nerve action

potentials, namely, the FitzHugh–Nagumo model (see Section 7.5, equations (7.39)), to

periodic impulses and demonstrated some of the important phenomena we discuss in

this chapter.

As we shall show in Chapter 1, Volume II, the spatial propagation of impulses in

neurons normally relies on a threshold stimulus being applied, and is an important prac-

9.1 Phase Resetting in Oscillators 279

tical example of an excitable medium. The heart pacemaker problem and some kinds of

cardiac failure are probably related to wave phenomena associated with perturbed oscil-

lators; see, for example, the general scientiﬁc article by Winfree (1983b). This area has

been studied over a period of some years, speciﬁcally in relation to heart failure and is

one of the motivations for the material described in this section. The results and conclu-

sions in this section, however, are quite general and are, in effect, model-independent,

even though we use speciﬁc models for pedagogical reasons.

By way of introduction we brieﬂy describe some of the experimental observations

made on the approximately 24-hour rhythmic emergence of fruit ﬂies from their pupae.

During the pupal stage of the ﬂies’ development, a metamorphosis takes place which

culminates in the emergence of an adult fruit ﬂy. If metamorphosing pupae are simply

left alone in a typical diurnal cycle of light and dark the ﬂies emerge in quanta over a

period of about 6 to 8 hours roughly every 24 hours. If such pupae are now placed in

complete darkness the ﬂies continue to emerge in almost exactly the same way; Fig-

ure 9.1 illustrates the aggregated results of numerous experiments.

If the pupae, in the dark environment, are now subjected to a brief pulse of light,

the timing, or phase, of the periodic emergence of the ﬂies is shifted. In other words

there is a phase shift in the underlying biological clock. The phase shift depends both

on the timing T of the light pulse and its duration or rather the number D in ergs/cm

transmitted by the light. We are interested in the emergence time T

after the pulse

of light; T

depends on T and D. If the dose D = 0 is given at T then clearly the

phase shift is zero; T

= 24 − T hours. Winfree (1975) gives the results of numerous

experiments in which T and D are varied and T

recorded. The important point to

note at this stage about these experiments is that there is a critical dose D

∗

which, if

administered at a speciﬁc time T

∗

, results in no further periodic emergences but rather a

Figure 9.1. Fruit ﬂy pupae were placed in a completely dark environment. Fly emergence (eclosion) takes

place approximately every 24 hours over a period of about 7 hours until all the pupae have matured. Here we

are concerned with the periodic peak timing, not the number emerging at each peak. (Redrawn from Winfree

1980 with permission)

280 9. Perturbed and Coupled Oscillators and Black Holes

continuous emergence. In other words the periodic behaviour has been destroyed. What

is also surprising from the data is just how small the dose was which caused this; see

Winfree (1975). Basically these experimental results suggest that there is a critical phase

and stimulus which destroy the basic underlying periodic behaviour or biological clock.

This has important implications for oscillators in general.

This section and the following three are principally concerned with biological oscil-

lators, the effect of stimulus and timing on the periodic behaviour and the experimental

evidence and implications. With the fruit ﬂy experiments there is a singularity (or sin-

gularities) in the stimulus-timing-response space of the oscillator at which point the

oscillator simply quits or does unpredictable things. Away from this singularity the sub-

sequent behaviour is more or less predictable. Later, in Section 9.4, we describe other

stimulus experiments, namely, on cardiac tissue, which exhibit similar phase singularity

behaviour.

Prior to doing the analysis, which is very easy for the illustrative example we con-

sider, it is helpful to consider the simple pendulum to demonstrate the phenomena of

phase resetting and stimulus-timing-phase singularity that we have just described. Sup-

pose a pendulum is swinging with period ω, and suppose we measure zero phase or time

t = 0 from the time the pendulum bob is at S, its highest point, at the right, say. Then

every time t = nω for all integers n, the bob is again at S. If, during the regular oscilla-

tion, we give an impulse to the bob, we can clearly upset the regular periodic swinging.

After such an impulse or stimulus, eventually the pendulum again exhibits simple har-

monic motion, but now the bob does not arrive at S every t = nω but at some other time

t = t

+ nω,wheret

is some constant. In other words the phase has been reset. If we

now give a stimulus to the bob when it is exactly at the bottom of its swing we can, if

the stimulus is just right, stop the pendulum altogether. That is, if we give a stimulus of

the right size at the right phase or time we can stop the oscillation completely; this is

the singular point in the stimulus-phase-response space we referred to above in the fruit

ﬂy experiments.

Suppose that an oscillator is described by some vector state variable u which satis-

ﬁes the differential equation system

= f(u,λ), (9.1)

where f is the nonlinear rate function and λ denotes the parameters of the oscillator. For

visual clarity and algebraic simplicity, suppose (9.1) describes a limit cycle oscillator

involving only 2 species, x and y. Then typically the limit cycle trajectory is a simple

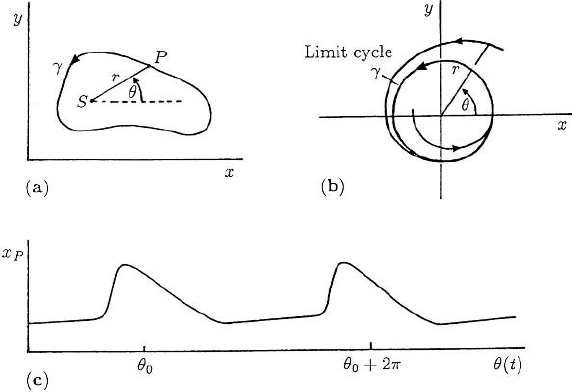
plane closed curve, γ say, in the two-dimensional species plane as in Figure 9.2(a). By

a suitable change of variable we can transform this limit cycle into one in which the

closed trajectory is a circle and the state of the oscillator is essentially described by an

angle θ, the ‘phase,’ with its origin at some arbitrary point on the circle. The limit cycle

is traversed with speed v = dθ/dt. In one complete traversal of the orbit, θ increases

by 2π.

A simple example of such a limit cycle system is

= R(r),

dθ

= Φ(r), (9.2)

9.1 Phase Resetting in Oscillators 281

Figure 9.2. (a) A typical limit cycle solution trajectory γ in the phase plane. (b) Typical solutions to the

system (9.2) with conditions (9.3). With any initial conditions, the solution evolves to the limit cycle given

by r = 1, dθ/dt = 1. (c) Typical time periodic behaviour of the point P in (a): note that the velocity of the

point P is in general not constant as is the case in (b).

where

R(r)



> 0

< 0

for



0 < r < r

r > r

, R(r

) = 0,Φ(r

) = 1. (9.3)

These conditions imply that (9.2) has a unique attracting limit cycle r = r

, dθ/dt = 1.

(A particularly simple case, mentioned before in Chapter 3, has R(r) = r(1 − r),

Φ(r) = 1, for which the solution can be given trivially.) If we normalise the circle with

respect to r

we can then take the limit cycle to be r = 1.

Figure 9.2(b) illustrates a typical phase plane limit cycle solution. Figure 9.2(c)

shows, for example, how the point x

= x

+ cos θ(t),wherex

is the steady state in

Figure 9.2(a), might vary as a function of t, with equivalent values of θ marked at two

points.

The fact that limit cycle solutions can be visualised as motion around a circle has

been developed in an intuitive way by Winfree (2000) under the general topic of ring

dynamics. The topological aspects are interesting and produce some unexpected results

and new concepts. Here we consider only the basic elements of the subject but they are

sufﬁcient to demonstrate certain important concepts.

With the modelling of physiological oscillators in mind we envisage some event,

a heart beat, for example, to occur at some speciﬁc value of the phase, which we can

normalise to θ = 0. The pacemaker goes through a repeating cycle during which it ﬁres

at this speciﬁc phase (that is, time), then is refractory for part of the cycle, after which

it again ﬁres, and so on. With the ring or circle concept for an oscillator, we can think

of the pacemaker as a point moving round a ring at a constant velocity with ﬁring oc-

curring every time the point passes through the position on the circle with phase θ = 0.

282 9. Perturbed and Coupled Oscillators and Black Holes

Although from a time point of view, t increases linearly, at speciﬁc times (multiples of

the period) the pacemaker ﬁres. To appreciate the basic concept of phase resetting of an

oscillator by a stimulus we take, as an illustrative example, the simplest nontrivial limit

cycle oscillator system

= r(1 −r),

dθ

= 1, (9.4)

for which the phase θ(t) = θ

+t, modulo 2π ; see Figure 9.2(b). With it we discuss the

two basic types of phase resetting, namely, Type 1 and Type 0.

9.2 Phase Resetting Curves

Type 1 Phase Resetting Curves

Suppose we ﬁrst perturb only the phase so that the governing equation becomes

r = 1,

dθ

= 1 +v(θ, I ), (9.5)

where v(θ, I ) represents the imposed velocity change, that is, the stimulus, on the an-

gular velocity dθ/dt. I is a parameter which represents the magnitude of the impulse

imposed on the oscillator. Again for pedagogical reasons let us take a simple, but non-

trivial, v which depends on θ and I , and which was used by Winfree (1980), namely,

dθ

= 1 + I cos 2θ, (9.6)

where I may be positive or negative. If the stimulus I is imposed at t = 0andmain-

tained for a time T then integrating (9.6) gives the new phase φ in terms of the old phase

θ when the stimulus was started. From (9.6),



(1 + I cos 2s)

−1

ds =



dt = T, (9.7)

which integrates to give

| I | < 1: tan φ = A tan[TB+tan

−1

tan θ)],

I = 1: tan φ = 2T +tan θ

I =−1: tan φ =

tan θ

1 −2T tan θ

| I | > 1: tan φ = A

|K |+1

|K |−1

if | tan φ | > A

tan φ = A

|K |−1

|K |+1

if | tan φ | < A

K =



A +tan θ

A −tan θ



exp (2TB),

(9.8)

9.2 Phase Resetting Curves 283

where

A =



|1 + I |

|1 − I |



1/2

, B =[|1 − I

1/2

. (9.9)

These give, explicitly, the new phase φ as a function of the old phase θ and the

strength I and duration T of the stimulus. So, applying a stimulus causes a phase shift

in the oscillator; in other words it resets the phase. For t > T the oscillator simply

reverts to dθ/dt = 1 but now there is a phase shift. This means that the oscillator will

ﬁre at different times but at the same value of the phase that it did before; the subsequent

period, of course, is also the same as it was before the stimulus. That is, the periodic

‘wave’ form such as in Figure 9.2(c) will simply be moved along a bit.

We are interested in the phase resetting curve of φ as a function of θ for various

stimulus magnitudes, which depend on I and its duration T . An important point with

stimuli like that in (9.5) is that dφ/dθ>0forallI , T and θ. This says that a later new

phase φ results if the impulse is applied at a later old phase. This is seen immediately

with the v in (9.6) by differentiating (9.8) with respect to θ and noting that it gives an

expression for dφ/dθ which is strictly positive. If we now plot the new phase φ against

the old phase θ when the impulse was applied, we obtain the phase resetting curve,

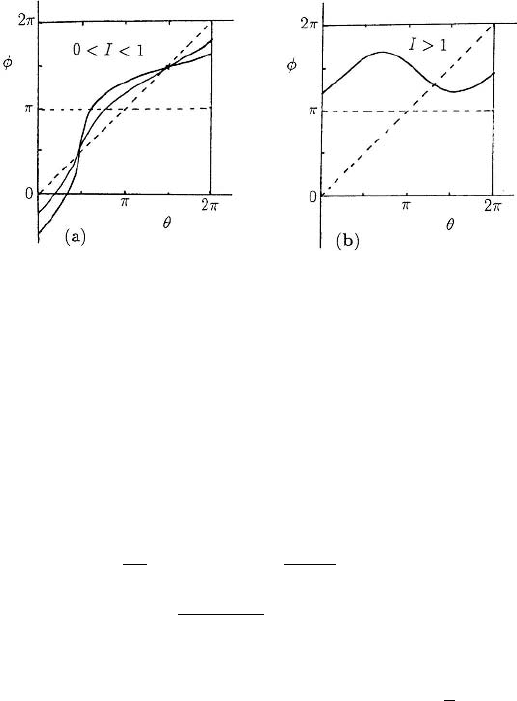
which is typically as shown in Figure 9.3. Note that whatever the stimulus I,thevalues

of the new phase φ cover the complete phase cycle, here 0 to 2π.Inotherwordsanynew

phase 0 <φ≤ 2π can be obtained by a suitable choice of an old phase 0 <θ≤ 2π

and the stimulus I.ForagivenI and T the new phase φ is uniquely determined by

the old phase θ. This is known as a Type 1 phase resetting curve and it is characterised

by the fact that dφ/dθ>0forall0<θ≤ 2π: the average gradient over a cycle is

1—hence the name. Although in Figure 9.3 there is an advance for I in 0 <θ<π,

another oscillator could well display a delay. The main point is that dφ/dθ>0inType

1 resetting.

Figure 9.3. Typical Type 1 phase resetting curves,

giving the new phase in terms of the old phase for

the phase velocity stimulus given by (9.6) for I ≥ 0

and T ≥ 0. This case shows a phase advance for an

impulse in 0 <θ<πandadelayforπ<θ<2π .

284 9. Perturbed and Coupled Oscillators and Black Holes

If I is sufﬁciently strong, |I | > 1 in fact, the phase velocity dθ/dt = 1 + v(θ, I)

can become negative for some phases: in the case of (9.6) this is for θ satisfying 1 +

I cos 2πθ < 0. This means that during the time of stimulation there is a phase attractor

and a phase repellor, where dθ/dt = 0andwhered[dθ/dt]/dθ is negative and positive

respectively (recall the stability analysis of single population models in Chapter 1). The

stimulus is not sustained for all time, so the oscillator resumes its periodic cycle after

the stimulus is removed—but of course with a different phase as determined by (9.8).

Type 0 Phase Resetting Curves

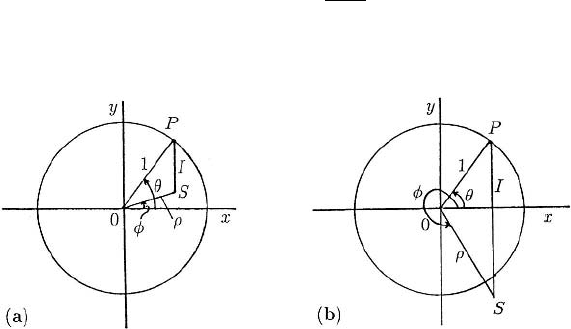
Consider the same limit cycle (9.4) but now let us subject it to a stimulus I which moves

the solution off the limit cycle r = 1. To be speciﬁc, let us take I as an impulse parallel

to the y-axis as shown in Figure 9.4. The analysis goes through with any perturbation

but the algebra is more complicated and simply tends to obscure the main point. Let us

decide on the notation that I > 0 is the situation illustrated in Figure 9.4; that is, with

0 <θ<π/2 the new phase φ is less than the old phase θ and the new position in

general has r = ρ = 1. We now want the new phase φ in terms of the old phase θ and

the stimulus I. From the ﬁgure

ρ cos φ = cos θ, ρ sin φ + I = sin θ (9.10)

which, on eliminating ρ gives φ = φ(θ, I ) implicitly; this is a three-dimensional surface

in (φ, θ, I) space. As we shall see, it is the projection of this surface onto the (I,θ)

plane which is of particular interest. Before considering this, however, let us construct

phase resetting curves equivalent to those in Figure 9.3, namely, the new phase φ as a

function of the old phase θ for various stimuli I : these are the projections of the surface

φ = φ(θ, I ) onto the (φ, θ) plane for various I .

From (9.10),

tan φ = tan θ −

cos θ

, (9.11)

Figure 9.4. The impulse I takes the point P (r = 1, old phase = θ) instantaneously to S (r =

ρ, new phase = φ).(a)0< I < 1. (b) I > 1.

9.2 Phase Resetting Curves 285

Figure 9.5. (a) Phase resetting curves from (9.11) for 0 < I < 1. From (9.12) note that dφ/dθ>0forall

such I .(b) Phase resetting curves from (9.11) for I > 1. Here for a range of θ, dφ/dθ<0 and not all new

phases φ can be obtained.

which gives φ in terms of θ for a given I . Let us suppose ﬁrst that 0 < I < 1. Then it is

clear qualitatively from Figure 9.4 that for 0 <θ<π/2and3π/2 <θ <2π , φ<θ,

while for π/2 <θ<3π/2, φ>θ. Thus the qualitative phase resetting curve φ against

θ is as shown in Figure 9.5(a): it crosses the zero stimulus diagonal at θ = π/2, 3π/2.

The quantitative details are not important here. From (9.11), differentiating with respect

to θ gives

(1 + tan

φ)

dφ

dθ

= 1 +tan

θ −

I sin θ

cos

1 − I sin θ

cos







> 0forall0<θ<2π, if | I | < 1.

< 0forθ such that sin θ>

(9.12)

So, on the phase resetting curves, if 0 < I < 1, dφ/dθ>0forallθ as illustrated in

Figure 9.5(a). Comparing these with the curves in Figure 9.3, they are all topologically

equivalent, so Figure 9.5(a) is a Type 1 phase resetting curve. The same remarks hold if

−1 < I < 0.

Let us now consider I > 1. From (9.12) there is a range of θ where dφ/dθ<0.

Refer now to Figure 9.4(b) and let P move round the circle. We see that S never moves

into the upper half-plane. That is, as θ varies over the complete period of 2π ,atthe

very least φ never takes on any phase in the range (0,π); in fact, the exact range can

easily be calculated from (9.11) or (9.12). The phase resetting curve in this case is

qualitatively as shown in Figure 9.5(b). This curve is not topologically equivalent to

those in Figure 9.5(a). All phase resetting curves with I > 1 are topologically different

from Type 1 resetting curves. Phase resetting curves like those in Figure 9.5(b), namely,

curves in which as the old phase θ takes on all phase values in (0, 2π) the new phase φ

only takes on a subset of the full cycle range, are called Type 0 resetting curves. Note

that on such curves the gradient dφ/dθ<0 for some range of θ: the average gradient