Murray J.D. Mathematical Biology: I. An Introduction

Подождите немного. Документ загружается.

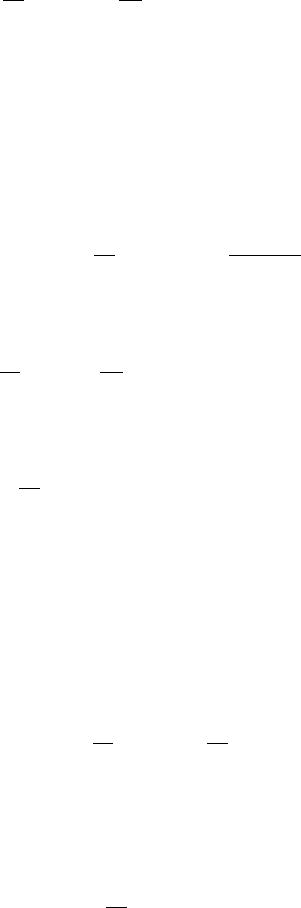
266 8. BZ Oscillating Reactions

x = x

, x = x

; y = y

, y = y

; z = z

, z = z

enclosing the steady state (x

, y

, z

) in (8.7) . Let us ﬁrst determine the planes x = x

and x = x

where 0 < x

< x

.Leti, j and k be the unit normals in the positive

x, y and z directions. On x = x

, n =−i and (8.19) requires

−i ·



x=x

=−



x=x

< 0 ⇒ qy − xy + x − x



x=x

> 0.

Since, from (8.4), 0 < q  1, and assuming x

= O(q), the last inequality requires x

to satisfy

y(q − x

) + x

− x

≈ y(q − x

) + x

> 0forally

≤ y ≤ y

So, at the least, a natural boundary for x < x

is x

= q, which we choose as a ﬁrst

approximation. Then on x = x

= q,

−i ·



x=x

=−

q(1 − q)

< 0ifq < 1.

On x = x

, n = i and (8.19) now requires

i ·



x=x



x=x

< 0 ⇒[y(q − x) + x − x

]

x=x

< 0.

If we choose x

= 1, we get

i ·



x=x

= ε

−1

y(q − 1)<0ifq < 1, for all y > 0.

With x

as given by (8.7) a little algebra shows that

q = x

< x

< 1ifq < 1.

With typical values for the parameters these conditions are satisﬁed.

Consider now the planes z = z

and z = z

,wherez

< z

.Onz = z

n =−k and (8.19) requires

−k ·



z=z

=−



z=z

=−(x − z)]

z=z

< 0

and since, on the boundary S, x ≥ x

we have a natural lower boundary for z of z =

= q. Strictly z

should be just less than q since x

= q.Nowonz = z

, n = k and

we require

k ·



z=z

< 0 ⇒ (x − z)]

z=z

< 0.

8.3 Nonlocal Stability of the FKN Model 267

Since x ≤ 1, an upper boundary for z is z = z

= 1; again we should have z

just

greater than 1.

Finally let us consider the planes y = y

and y = y

where y

< y

.On

y = y

, n =−j and (8.19) requires

−j ·



y=y

=[y(q + x) −2 fz]

y=y

< 0

and so we must have

2 fz

q + x

for all q ≤ x ≤ 1andq ≤ z ≤ 1.

So,

2 fq

q + 1

2 fz

minimum

1 + x

maximum

Thus, an appropriate lower boundary for y is

2 fq

q + 1

When y = y

, n = j and we need

j ·



y=y

< 0 ⇒ 2 fz− y(q + x)]

y=y

< 0

which implies

2 fz

q + x

for all q ≤ x ≤ 1andq ≤ z ≤ 1

and so we can take

2 fz

maximum

q + x

minimum

Again using (8.4), for typical values of q and f , y

< y

Finally we have (8.19) satisﬁed on the surface S of the rectangular box given by

x = q, x = 1; y =

2 fq

q + 1

, y =

; z = q, z = 1 (8.20)

within which the steady state (8.7) lies if f and q satisfy certain inequalities, which are

indeed satisﬁed by the parameter values in the Belousov–Zhabotinskii reaction.

268 8. BZ Oscillating Reactions

Figure 8.2. Comparison of the observed oscillations in the BZ reaction with the numerically computed so-

lution of the limit cycle solution of the model FKN system (8.5) with f = 0.3, δ = 1/3, q = 5 × 10

−3

ε = 0.01. (Redrawn from Tyson 1977)

This bounding surface could be reﬁned to give more accurate bounds on any so-

lutions of (8.5). Since the ultimate limit cycle solutions have to be found numerically,

or asymptotically as in the following section, all that is needed is a demonstration that

such a conﬁned set exists.

Figure 8.2 shows the numerical solution of the system (8.5) as compared with the

observed oscillations.

8.4 Relaxation Oscillators: Approximation for the

Belousov–Zhabotinskii Reaction

If we look again at Figure 8.1 we see that certain parts of the cycle are covered very

quickly. This is particularly evident in the trace of the Br

−

ion where it suddenly rises

along DA and drops as quickly along BC. As we mentioned above when parts of a

limit cycle are traversed quickly in comparison with other parts it is often referred to as

a relaxation oscillator. What this means from a modelling point of view is that a small

parameter must be present in the differential equation system in a crucial place to cause

this rapid variation in the solution.

To be speciﬁc, and to show how we can exploit such behaviour, consider ﬁrst the

simple relaxation oscillator

= y − f (x),

=−x, 0 <ε 1, (8.21)

where f (x) is a continuous function such that, say, f (x) →±∞as x →±∞.The

classic example, where f (x) = (1/3)x

− x, is known as the Van der Pol oscillator.

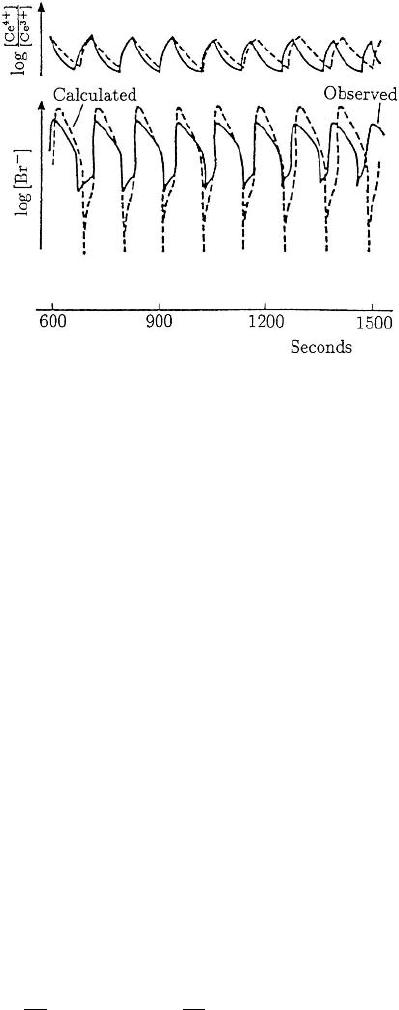
8.4 Relaxation Oscillators 269

Figure 8.3. (a) Typical limit cycle phase trajectory ABCDA for a relaxation oscillator. The two horizon-

tal parts of the trajectory are traversed very quickly. (b) The solution x(t) corresponding to the limit cycle

trajectory in (a).

System (8.21) is a typical singular perturbation problem (see, for example, the book by

Murray 1984) since ε multiplies one of the derivatives. Figure 8.3(a) illustrates a typ-

ical limit cycle phase plane trajectory for (8.21), with Figure 8.3(b) the corresponding

solution x(t).

From the ﬁrst of (8.21), except where y ≈ f (x), x changes rapidly by O(1/ε).So,

referring now to Figure 8.3(a), along DA and BC, x(t) changes quickly. Along these

parts of the trajectory the appropriate independent variable is τ = t/ε rather than t.

With this transformation the second of (8.21) becomes, as ε → 0,

dτ

=−εx ⇒ y ≈ constant,

as it is on DA and BC in Figure 8.3(a). From (8.21), along the null cline y = f (x)

between AB and CDthe second equation becomes



(x)

≈−x (8.22)

which can be integrated to give x implicitly as a function of t.If f (x) is the Van der Pol

cubic above, or can be reasonably approximated by a piecewise linear function, then we

can integrate this equation exactly. We can then estimate (which we do in detail below)

the period T of the oscillation since the major contribution comes from the time it takes

to traverse the branches AB and CD: the time to move across DA and BC is small,

o(1). It can be shown that if T is the limit cycle period calculated in this manner from

(8.22), then the asymptotic limit cycle period of (8.21) has a correction of O(ε

2/3

).For

our purposes all we need is the O(1) approximation for T .

By way of example, suppose f (x) = (1/3)x

− x, that is, (8.21) is the simple Van

der Pol oscillator, and let us calculate the O(1) period T . The null cline y = f (x) here

and the limit cycle relaxation trajectory are very similar in shape to those illustrated

in Figure 8.3 except that the origin has been moved to a point halfway down DB in

Figure 8.3(a) and to a point in Figure 8.3(b) such that the solution is symmetrical about

the x = 0 axis. From the above analysis, on integrating from the equivalent of A to B

270 8. BZ Oscillating Reactions

in Figure 8.3(a) and from the equivalent of C to D,asε → 0 the period T to O(1) is

given by (8.22), with f (x) = (1/3)x

−x. A little algebra gives A as (2, 2/3) and B as

(1, −2/3). Because of the symmetry, and to be speciﬁc if we take t = 0atA,theO(1)

period T is given by





x −



dx =−



T/2

dt ⇒ T = 3 −2ln 2. (8.23)

Note that even if we cannot integrate f



(x)/x simply, to get the period, we can still

determine the maxima and minima of the limit cycle variables simply from the algebra

of the null clines y = f (x). These correspond to A and C for x(t) and D or A and B

or C for y(t).

On comparing the bromide ion concentration [Br

−

] as a function of time in Fig-

ure 8.1 and the limit cycle time-dependent solution sketched in Figure 8.3(b) it is rea-

sonable to look for a relaxation oscillator type of approximation for the BZ oscillator.

This has been done by Tyson (1976, 1977) whose analysis we effectively follow in the

next section.

Let us again consider the FKN mechanism in the dimensionless form (8.5); namely,

= qy − xy + x(1 − x),

=−qy − xy + 2 fz,

= x − z,

(8.24)

with the dimensionless parameters given by (8.4). Note that ε  δ, in which case we

can reduce the order of the system (8.24) by setting ε dx/dt ≈ 0. This gives

0 = qy − xy + x(1 − x) ⇒ x = x(y) =



(1 − y) +[(1 − y)

+4qy]

1/2



(8.25)

With this (8.24) reduces to the second-order differential equation system in y and z:

= 2 fz− y[x(y) +q],

= x(y) − z,

(8.26)

which of course can now be analyzed completely in the (y, z) phase plane. We can,

in the usual way, determine the steady state, analyze the linear stability, show there is

a conﬁned set and hence determine the conditions on the parameters for a limit cycle

solution to exist.

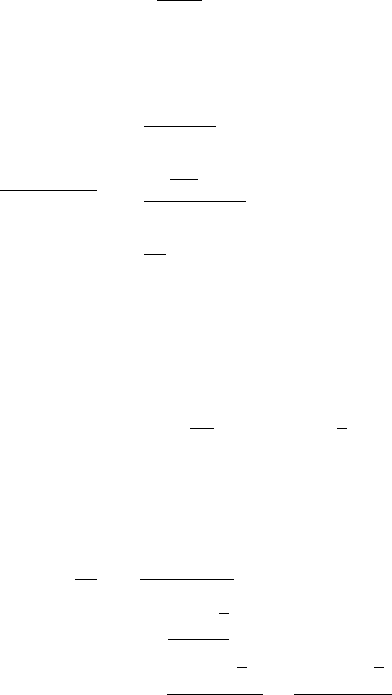
8.5 Limit Cycle Oscillation Relaxation Model Analysis 271

8.5 Analysis of a Relaxation Model for Limit Cycle Oscillations in

the Belousov–Zhabotinskii Reaction

Here we exploit the relaxation oscillator aspects of (8.26) and hence determine the ap-

proximate period of the limit cycle, the maxima and minima of the dependent variables

and then compare the results with the experimental observations of the oscillating re-

action. To do this we ﬁrst give approximations for x(y) using the fact that 0 < q  1

from (8.4), and then sketch the null clines.

From (8.25), with q  1, the z-null cline from (8.26) is

z = x(y) ≈



1 − y

y −1

for



q  1 − y ≤ 1

q  y − 1

. (8.27)

The y-null cline, from (8.26), is

z =

y[x(y) + q]

≈











y(1 − y)

2 f



y−1



2 f

for







q  1 − y  1

q  y − 1

y  1

. (8.28)

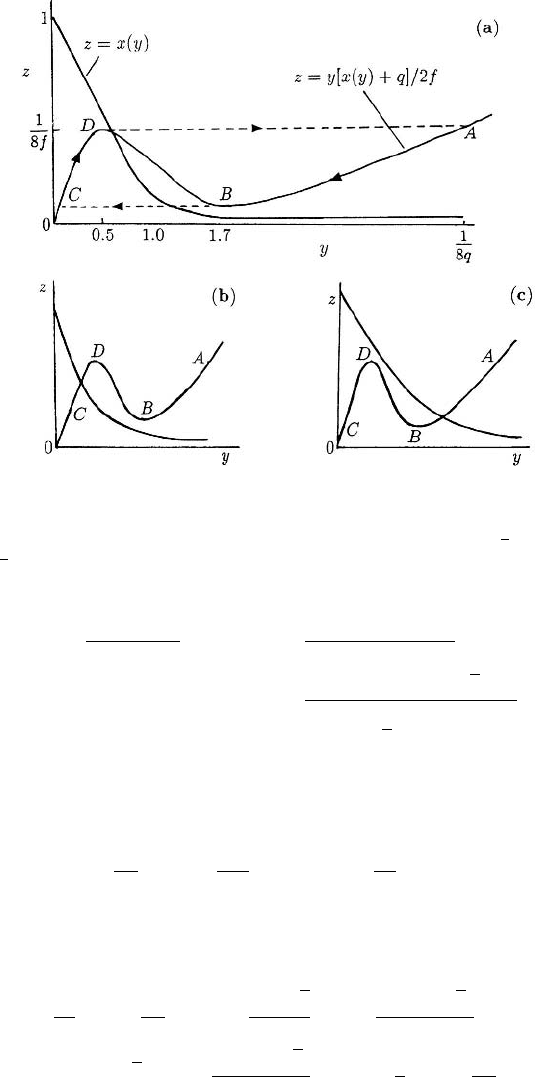
The z-null cline is a monotonically decreasing function of y; it is sketched in Figure 8.4.

The y-null cline, also shown in Figure 8.4 for various ranges of f , has a local maximum,

max

(= z

= z

in Figure 8.4(a))

max

8 f

at y

max

, (8.29)

obtained from the ﬁrst of (8.28). From the second of (8.28), z has a local minimum, z

min

(= z

= z

in Figure 8.4(a)) at



2 f (y − 1)



{2y

−4y +1}=0

⇒ y

min

2 +

√

⇒ z

min

q(1 +

√

2 f

q(3 + 2

√

2 f

(8.30)

The values of z and y at the relevant points A, B, C and D are obtained from (8.27)

and (8.28), with z

(= z

) and y

given by (8.29) and z

(= z

) and y

from (8.30).

For y

, we have from the ﬁrst of (8.28), with q  1andz

= z

min

from (8.30),

272 8. BZ Oscillating Reactions

Figure 8.4. Schematic null clines for the reduced BZ model system (8.26) using the asymptotic forms for

0 < q  1 from (8.27) and (8.28). The points B and C correspond to z

min

given by (8.30) and the points

D and A to z

max

in (8.29). The asymptotic expressions for A, B, C and D are gathered together in (8.31)

below. Note how the position of the steady state changes with f :(a)1/4 < f <(1 +

√

2)/2; (b) f < 1/4;

√

2)/2 < f .

(1 − y

)

2 f

⇒ y

1 −[1 −8 fz

]

1/2

≈

1 −[1 −4q(3 + 2

√

2)]

1/2

≈ q(3 +2

√

2).

For y

, we have, from the second of (8.27) for y large, z ∼ qy/f ,andz

= z

max

from

(8.29),

8 f

= z

≈

⇒ y

≈

 1.

Gathering together these results, and those from (8.29) and (8.30), we have, for the

points ABCD in Figure 8.4(a),

≈

, z

8 f

; y

≈

2 +

√

, z

≈

q(3 + 2

√

2 f

;

≈ q(3 +2

√

2), z

≈

q(3 + 2

√

2 f

; y

≈

, z

≈

8 f

(8.31)

8.5 Analysis of a Relaxation Model for Limit Cycle Oscillations 273

Figures 8.4(a) to (c) illustrate the various null cline possibilities for the reduced BZ

model (8.26). From (8.27), (8.28) and (8.31) we can get the f -ranges where each holds.

Figure 8.4(b) is when the local maximum at z

lies to the right of the steady state. This

requires that on the z-null cline, given by (8.27),

y=y

< z

⇒ x(y

) ≈ 1 − y

< z

⇒ f <

, (8.32)

on using (8.31). Figure 8.4(a) holds when z on the z-null cline is such that

y=y

> z

and z]

y=y

< z

which gives

x(y

) ≈ 1 − y

8 f

and x(y

) ≈

−1

q(3 + 2

√

2 f

which reduces to

< f <

1 +

√

. (8.33)

Finally Figure 8.4(c) holds when, on the z-null cline,

y=y

> z

⇒ f >

1 +

√

. (8.34)

We know from Chapter 7 that Figure 8.4(a) is a case in which a limit cycle oscilla-

tion is possible. So, with f in the range (8.33) and the steady state unstable, the reduced

BZ model system (8.26) will exhibit limit cycle solutions. Now comparing Figure 8.4(a)

with the relaxation limit cycle oscillator in Figure 8.3(a) gives the O(1) period of the

oscillatory solution of (8.26) for 0 <δ 1as

T ≈



dt +



dt =









−1

dz (8.35)

with dz/dt given by (8.26). So,



[x(y) − z]

−1

dz. (8.36)

To get an exact evaluation to O(1) for q  1, it is convenient to change the variable

to y, with z as a function of y given by the second of (8.28), since AB is part of the

y-null cline. It is a tedious integration. All we want here is a reasonable approximation

to the period. So, using the expressions for q  1 in (8.27), we have, along most of

AB,

x(y) ≈

y −1

∼ q,

274 8. BZ Oscillating Reactions

and so, using (8.31),



(q − z)

−1

dz = ln



−q



∼ ln









8 f





q(3+2

√

2 f

−q









∼−ln [4(3 −2 f + 2

√

2)q], q  1.

(8.37)

This, in fact, is an upper bound for T

since on AB, x(y) ≈ qy/(y − 1),which

asymptotes to q only for y  1. On AB, x(y) goes from

x(y

) =







−1



∼ q + O(q

), q  1,

x(y

) =



√





√

−1



= q(1 +

√

2).

Returning to the integral in (8.36) we have T

bounded above by (8.37) and below by

the expression there with q(1 +

√

2) replacing q.Thatis,

ln [4(3 − 2 f + 2

√

2)q] < T

< −ln [4(3 − 2 f + 2

√

2)(1 +

√

2)q]. (8.38)

Let us now evaluate the T

contribution to the period in (8.35), namely,



[x(y) − z]

−1

dz.

It is also convenient here to change to y as the integration variable. Between C and D

in Figure 8.4(a) and on CD

x(y) ≈ 1 − y, z ≈

y(1 − y)

2 f

⇒ dz =



1 −2y

2 f



so the last integral gives, after some further tedious algebra,

≈





1−2y

2 f





(1 − y) −

y(1−y)

2 f



=−



4 f − 1

2 f − 1





1/(4 f −1)

4 f − 1

4 f



(8.39)

8.5 Analysis of a Relaxation Model for Limit Cycle Oscillations 275

The period to O(1) for q  1 is then given as a function of f and q by T

+ T

using (8.38) and (8.39). The dimensional period is given by multiplying T by t

from

(8.4).

To complete the analysis of the relaxation oscillator we have to integrate the ap-

proximate equations on the branches AB and CD. We have effectively already done

this when we evaluated T

and T

.Letustaket = t

= 0 and hence z(0) = z

for algebraic convenience. Then on AB, with x(y) ∼ q for y large from (8.27), (8.26)

gives

≈ q − z ⇒ z(t) = z

−t

+q(1 −e

−t

), (8.40)

and so there is an exponential decay in time from z

to z

= O(q) for times of O(1).

On CD, x(y) ≈ 1 − y and z ≈ y(1 − y)/(2 f ) so the second of (8.26) on changing

to the variable y,gives



1 −2y

2 f



≈ (1 − y) −

y(1 − y)

2 f

which integrates to give y implicitly as a function of t from



1 − y

(2 f − y)

4 f −1



= K +(2 f − 1)t, (8.41)

where K is an integration constant. Since the time to traverse the horizontal part of the

trajectory, namely, BC, is negligible, we can determine K by taking y(t

) = y

,where

t = t

≈ t

, with t

given by (8.40) on setting z = z

;thatis,

= ln



(1 − q)

−q



. (8.42)

From (8.41) and the last equation we thus have

K = ln



1 − y

(2 f − y

)

4 f −1



−(2 f − 1)t

. (8.43)

Now with y(t) given implicitly by (8.41), we get z from z ∼ y(1 − y)/(2 f ). Finally

the time to traverse DA is also negligible. We thus have analytical expressions for the

dependent variables in the relaxation oscillator as functions of time for 0 < q  1.

Let us now return to the actual BZ reaction and recall from (8.1) that z and y

are the dimensionless variables associated with the catalyst form Ce

and bromide

ion Br

−

respectively. Referring to Figure 8.4(a) and starting at A, say, the limit cycle

oscillation trajectory then goes through BCD to A again. This trajectory corresponds

to the experimentally obtained cycle illustrated in Figure 8.1 with corresponding letters.

The [Br

−

] decreases exponentially to B, then there is a rapid drop to the value at C.The

value at B is the threshold Br

−

concentration described in Section 8.1 where process II

takes over from process I. There is then an increase in times O(1) from C to D,given