Mourachkine A. Room-Temperature Superconductivity

Подождите немного. Документ загружается.

34 ROOM-TEMPERATURE SUPERCONDUCTIVITY

(0)

Normal

state

Meissner state

= 0;

= 0

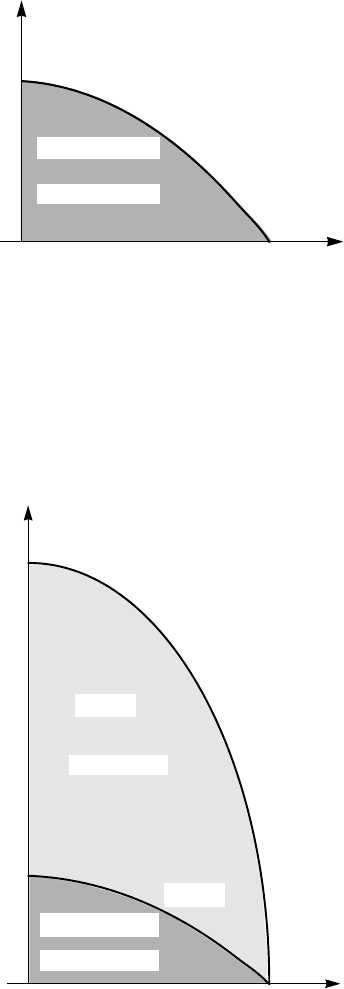
Figure 2.8. H

(T ) dependence for a type-I superconductor, shown schematically.

cylinder with its axis parallel to the external magnetic ﬁeld. Inside the cylinder,

the superconducting order parameter Ψ is zero.

The radius of the cylinder is of the order of the coherence length ξ

. The

supercurrent circulates around the vortex within an area of radius ∼ λ, the

(0)

Normal

state

(0)

(

)

≠

Mixed state

(

)

Meissner state

= 0;

= 0

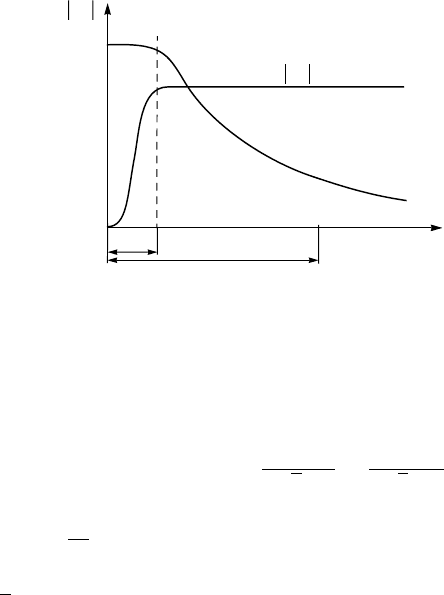
Figure 2.9. H

(T ) and H

(T ) dependences for a type-II superconductor, shown schemati-

cally.

Basic properties of the superconducting state 35

penetration depth (see Fig. 2.25). The spatial variations of the magnetic ﬁeld

and the order parameter inside and outside an isolated vortex are illustrated in

Fig. 2.10. The vortex state of a superconductor, discovered experimentally

by Shubnikov and theoretically by Abrikosov, is known as the mixed state.It

exists for applied ﬁelds between H

and H

.AtH

, the superconductor

becomes normal, and the ﬁeld penetrates completely. Depending on the ge-

ometry of a superconducting sample and the direction of an applied ﬁeld, the

surface sheath of the superconductor may persist to even higher critical ﬁeld

, which is approximately 1.7H

Figure 2.10. The spatial variations of the magnetic ﬁeld H and the order parameter Ψ in-

side and outside an isolated vortex in an inﬁnite superconductor. R is the distance from the

center of the vortex, and ξ

and λ are the coherence length and the penetration depth of the

superconductor, respectively (in type-II superconductors, ξ

<λ).

As we shall see further below, the Ginzburg-Landau theory predicts that

(T )λ(T )ξ

(T )=

¯h

√

2eµ

√

2πµ

, (2.21)

where Φ

≡

=2.0679 × 10

−15

(or Weber) (2.22)

is the magnetic ﬂux quantum. In the frameworkof the Ginzburg-Landautheory,

√

2kH

, where k = λ/ξ

is the Ginzburg-Landau parameter. Then,

substituting this expression into Eq. (2.21), we obtain

=2πξ

. (2.23)

This important relation is often used to obtain the values of the coherence

length in type-II superconductors.

The magnitudes of the upper critical magnetic ﬁeld of conventional type-II

superconductors is very small, less than 1 T. However, in unconventional super-

conductors, these values can be extremely large (see Table 2.2). For example,

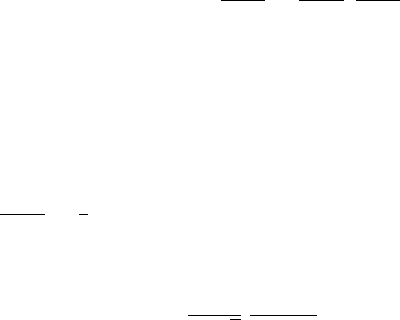
36 ROOM-TEMPERATURE SUPERCONDUCTIVITY

in the Chevrel phase PbMo

, H

= 60 T. In three-layer high-T

supercon-

ductors, the critical magnetic ﬁeld parallel to the c-axis can be H

(0) ∼ 50 T

and parallel to the ab-planes H

(0) ∼ 250 T.

3.8 Critical current

The superconducting state can be destroyed not only by a magnetic ﬁeld

butbyadc electrical current as well. The critical current J

is the maximum

current that a superconductor can support. Above J

, the dc current breaks the

Cooper pairs, and thus, destroys the superconducting state. In other words, J

is the minimum pair-breaking current. Thus, any superconductor is character-

ized by a critical dc current density j

(current divided by the cross-sectional

area through which it ﬂows).

The temperature dependence J

(T ) (or j

(T )) is similar to that of H

(T ),

shown in Fig. 2.8. At T = 0, the critical current density can be estimated by

using the electron velocity on the Fermi surface, v

= π∆ ξ

/¯h, the superﬂuid

density n

given by Eq. (2.9), and the critical (maximum) velocity of a Cooper

pair, v

 ∆/mv

,as

= n

 n

∆

¯hc

16πe

, (2.24)

where m is the electron mass. To estimate j

, we take λ

∼ 10

◦

and ξ

∼

◦

. Substituting these values into Eq. (2.24), together with c  3 × 10

cm/s, ¯h = h/2π  10

−27

erg s and e =4.8 × 10

−10

esu, we obtain j

∼

4 × 10

CGS units. In Si units, it is equivalent to j

∼ 10

Acm

−2

The critical current density j

in Eq. (2.24) can be expressed in terms of crit-

ical magnetic ﬁeld H

(0). Using the expressions for the condensation energy

(see below)

(0)

8π

N(0)∆

(0), where N(0) = k

m/(π ¯h)

is the density

of states near the Fermi surface, the electronic density n

(0) = k

/3π

, and

=¯hv

/(π∆(0)), we obtain in CGS units



4π

√

(0)

. (2.25)

The Ginzburg-Landau and BCS theories give the same relation for j

with

somewhat different numerical prefactors.

From Eq. (2.25), the maximum current density that can theoretically be

sustained in a superconductor, is of the order of H

/λ

(in SI units). Let us

estimate j

. Using B

∼ 0.1 T, λ

∼ 10

◦

, and µ

=4π 10

−7

H/m, we

obtain j

≈ 5 × 10

Acm

−2

3.9 Energy scales

The superconducting state is characterized by a few energy scales. We al-

ready considered one energy scale given by the critical temperature, k

. The

Basic properties of the superconducting state 37

superconducting state is also characterized by an pairing energy gap, phase-

coherence gap, phase stiffness and condensation energy. Let us consider the

meaning of these energy scales.

3.9.1 Pairing energy gap

The pairing energy gap 2∆

measures the strength of the binding of elec-

trons (quasiparticles) into the Cooper pairs. In other words, the value of this

gap corresponds to the binding energy that holds the electrons together. The

magnitude of pairing energy gap is temperature-dependent.

As discussed above, the superconducting state requires the electron pairing

and the onset of long-range phase coherence. They are two independent phe-

nomena and, generally speaking, occur at different temperatures, T

pair

and

, respectively, and T

≤ T

pair

. In conventional superconductors, how-

ever, T

pair

= T

. At the same time, in most unconventional superconduc-

tors, T

pair

. In a superconductor, the value of the phase stiffness (relative

to k

) determines whether the electron pairing and the onset of long-range

phase-coherence occur simultaneously or not.

The pairing gap is directly related to the k

pair

energy scale, thus,

2∆

∝ k

pair

. At the same time, the magnitude of the phase-coherence

gap is proportional to k

, i.e. 2∆

∝ k

. In general, the coefﬁcients

of proportionality in this two expressions are different and, as determined ex-

perimentally, varies between 3.2 and 6, depending on the case (in one heavy

fermion,  9). The energy 2∆

measures the strength of the binding of two

electrons (quasiparticles) into a Cooper pair. At the same time, the energy 2∆

is the condensation energy of a Cooper pair due to onset of phase coherence

with other pairs. We shall discuss the phase-coherence gap in the following

subsection.

Historically, conventional superconductors are the most studied. Further-

more, the physics of conventional superconductors is simpler than that of un-

conventional superconductors, because conventional superconductors have only

one energy gap. Thus, let us discuss for the rest of this subsection the energy

gap exclusively in conventional superconductors. The reason why the binding

energy of two electrons is called the energy gap is because, when a metal un-

dergoes a transition into the superconducting state, a small energy gap appears

in the band at the Fermi level. As a result, the electronic system is unable to

absorb arbitrary small amounts of energy.

The energy gap in a superconductor is quite different in its origin from that

in a semiconductor. From the band theory, energy bands are a consequence of

the static lattice structure. In a superconductor, the energy gap is far smaller,

and results from an attractive force between electrons in the lattice which plays

only an indirect role. In a superconductor, the gap occurs on either side of the

Fermi level, as shown in Fig. 2.11. If, in a semiconductor, the energy gap is

38 ROOM-TEMPERATURE SUPERCONDUCTIVITY

∆

T = 0

Superconductor

Normal metal

Figure 2.11. The density of states near the Fermi level E

in a superconductor, showing the

energy gap 2∆ at T = 0, and in a normal metal. All the states above the gap are assumed empty

and those below, full.

tied to the Brillouin zone (see Chapter 5), in a superconductor, the energy gap

is carried by the Fermi surface. At T = 0 all electrons are accommodated in

states below the energy gap, and a minimum energy 2∆(0) must be supplied

to produce an excitation across the gap.

As discussed above, the phase coherence in conventional superconductors is

mediated by the overlap of the Cooper-pair wavefunctions—the process which

does not give rise to a “new” order parameter. Instead, it simply “magniﬁes”

the Cooper-pair wavefunctions to the level of the order parameter. Therefore,

the electron pairing and the phase coherence in conventional superconductors

occur simultaneously at T

,soT

pair

= T

. As a consequence, the energy

gap in the elementary excitation spectrum of conventional superconductors is

exclusively determined by the pairing energy gap, ∆=∆

The BCS theory, developed for conventional superconductors, predicts that

2∆(0) = 3.52k

. Experimentally, the ratio

2∆

in conventional super-

conductors varies between 3.2 and 4.2. Figure 2.12 shows the temperature

dependence of the energy gap in the framework of the BCS theory.

Since in unconventional superconductors, ∆

and k

do not relate with

one another, the ratio

2∆

determined experimentally in unconventional su-

perconductors, is usually larger than 4, and can be as large as 30.

Basic properties of the superconducting state 39

0.5

1.5

0 0.2 0.4 0.6 0.8 1

T/T

BCS dependence

∆/

1.76

Figure 2.12. The BCS temperature dependence of the energy gap ∆(T).

3.9.2 Phase-coherence energy gap

The phase-coherence energygap 2∆

is the condensation energyof a Cooper

pair when the long-range phase coherence appears. The condensation of Cooper

pairs is similar to a Bose-Einstein condensation which occurs in momentum

space (see Chapter 4). The magnitude of a phase-coherence gap istemperature-

dependent, and the temperature dependence of ∆

is similar to that in Fig.

2.12.

Generally speaking, the magnitudes of pairing and phase-coherence gaps

depend on orientation: ∆

(k) and ∆

(k), where k is the vector in momentum

space, and ∆

and ∆

have different symmetries. In many unconventional

superconductors, the pairing and phase-coherence gaps are highly anisotropic,

and often have nodes.

As was mentioned above, the variations of |Ψ| in momentum space are al-

ways proportional to variations of phase-coherencegap ∆

, and not to those of

∆

. In conventional superconductors, however, the symmetry of order param-

eter coincides with the symmetry of the pairing gap ∆

, because conventional

superconductors have only one energy gap: ∆=∆

3.9.3 Phase stiffness

The phase stiffness Ω

is the energy scale measuring the ability of the su-

perconducting state to carry supercurrent. The magnitude of phase stiffness

is mainly determined by zero-temperature superﬂuid density n

(0) and zero-

temperature coherence length ξ

(0). Thus, the phase stiffness is an energy

scale deﬁned at T =0.

40 ROOM-TEMPERATURE SUPERCONDUCTIVITY

The phase stiffness is given by the following expression

Ω

¯h

(0) ξ

(0)

∗

(¯hc)

(0)

16e

(0)

, (2.26)

where m

∗

is the effectivemass of charge carriers; λ

(0) is the zero-temperature

London penetration depth given by Eq. (2.9); c is the speed of light; and A is

a dimensionless number of the order of 1 which depends on the details of the

short distance physics [12]. For layered compounds, ξ

(0) → ξ

GL,⊥

(0) in

the above formula, where ξ

GL,⊥

(0) is the zero-temperature coherence length

perpendicular to the layers.

In order to determine the importance of phase ﬂuctuations, it is necessary to

compare the values of the phase stiffness and energy scale k

.Ifk



Ω

, phase ﬂuctuations are relatively unimportant. Then, the electron pairing

and the onset of long-range phase coherence occur simultaneously at T

.If

≈ Ω

, phase ﬂuctuations are important. In this case, theelectron pairing

will most likely occur above T

For example, the ratio Ω

calculated for some conventional super-

conductors lies between 2×10

and 2×10

[12]. This means that the superﬂuid

density in conventional superconductors is relatively high, and phase ﬂuctua-

tions in metal superconductors are practically absent. As a consequence, the

pairing and the onset of long-range phase coherence in low-T

superconductors

occur simultaneously at T

. However, phase ﬂuctuations play an important role

in unconventional superconductors. The ratio Ω

calculated for some

superconductors with low superﬂuid density and small coherence length, such

as organic and high-T

superconductors, is small and lies between 0.7 and 16

[12]. Thus, the pairing may occur well above T

which is controlled by the

onset of a long-range phase order.

3.9.4 Condensation energy

The superconducting state is a more ordered state than the normal one.

Therefore, the superconducting state is preferable to the normal state from

the standpoint of free energy. However, the superconducting state can be de-

stroyed by a critical magnetic ﬁeld H

which is related thermodynamically to

the free-energy difference between the normal and superconducting states in

zero ﬁeld. This difference is the condensation energy of the superconducting

state. Thus, the thermodynamic critical ﬁeld H

is determined by equating the

energy H

/(8π) per unit volume (in CGS units), associated with holding the

ﬁeld out against the magnetic pressure, with the condensation energy:

(T ) − F

(T )=

(T )

8π

, (2.27)

Basic properties of the superconducting state 41

where F

and F

are the Helmholtz free energies per unit volume in the re-

spective phases in zero ﬁeld. We shall discuss the condensation energy further

below while considering the thermodynamic properties of superconductors.

Let us now estimate the condensation energy of a superconductor. As dis-

cussed above, the condensation energy of a single Cooper pair is 2∆

. Then,

/2 × 2∆

is approximately the total condensation energy per unit volume,

where n

is the density of Cooper pairs in a superconductor. The fraction of the

electronic states directly involved in pairing approximately equals ∆

(0)/E

where E

is the Fermi energy. Recalling that a conventional superconductor

has only one energy gap ∆=∆

, the condensation energy of a conventional

superconductor is of the order of ∆

(0)/E

In a conventional superconductor, ∆(0) ∼ 0.5–1 meV and E

∼ 5–10 eV.

Then, ∆(0)/E

≈ 10

−4

, and the condensation energy is small as ∆

(0)/E

≈

−7

–10

−8

eV per atom.

4. Basic properties of the superconducting state

We already considered the most important characteristics of the supercon-

ducting state; we know why the superconducting state occurs, and what causes

superconductivity in solids. Now we are going to discuss basic properties of

the superconducting state. The mechanisms of superconductivity occurring in

different materials will be discussed in Chapters 5, 6 and 7. The Ginzburg-

Landau theory will be considered at the end of this chapter.

The superconducting state, as any state of matter, has its own basic proper-

ties, so any superconductor, independently of the mechanism of superconduc-

tivity and the material, will exhibit these properties. Hence, a room-temperature

superconductor will exhibit them too. The main basic properties of the super-

conducting state are the following: zero resistance, the Meissner effect, the

magnetic ﬂux quantization, the Josephson effects, the appearance of an energy

gap in elementary excitation energy spectrum, and the proximity effect. Every

superconducting transition is marked by a jump in speciﬁc heat. And lastly, in

the mixed state, the behavior of type-II superconductors has the same pattern.

4.1 Zero resistance

Every superconductor has zero resistivity, i.e. inﬁnite conductivity, for a

small-amplitude dc current at any temperature below T

. Is the resistivity of

a superconductor really zero? Yes, its resistivity is zero as far as it can be

measured. This property of the superconducting state was demonstrated by

inducing a small-amplitude dc current around a closed ring of a conventional

superconductor. The experiment continued over two and a half years—there

was no measurable decay of the current. This means that the resistivity of a

superconductor is smaller than 10

−23

Ω m. This value is 18 orders of magni-

42 ROOM-TEMPERATURE SUPERCONDUCTIVITY

tude smaller than the resistivity of copper at room temperature. Such a value

of resistivity in a superconductor implies that the current lifetime in a super-

conducting ring in zero magnetic ﬁeld is not less than 10

years.

This intrinsic property of the superconducting state is probably the most fas-

cinating one, and is widely used in different types of practical applications—

from microchips to power lines.

It is worth to recall that the resistivity of a superconductor to an ac current

is not zero. The ac current ﬂows on the surface of a superconductor within a

thin layer of thickness on the order of λ

4.2 The Meissner effect

From a classical point of view, every superconductor exhibits perfect dia-

magnetism, i.e. B = 0 inside the superconductor, as shown in Fig. 2.2b. In

fact, as we already know, the magnetic ﬁeld penetrates into the superconductor

within a very thin surface layer having the thickness of the order of λ

. To can-

cel B, a superconductor creates a dc current on the surface, which gives rise to

a magnetization M, so that in the interior of the superconductor 4πM + H =

0. Since the resistivity of the superconductor is zero, this surface current does

not dissipate energy.

If the magnetic ﬁeld was applied to a superconductor at T>T

, and it is

then cooled down to T<T

, in this case, the ﬁeld will remain inside the super-

conductor until it will be warmed up again through T

. This “frozen” magnetic

ﬁeld will remain inside the superconductor independently of the presence of

the external magnetic ﬁeld.

Probably, the most spectacular demonstration of the Meissner effect is the

levitation effect. A small magnet above T

simply rests on the surface of a

superconductor having dimensions larger than those of the magnet. If the tem-

perature is lowered below T

, the magnet will ﬂoat above the superconductor.

The gravitational force exerted on the magnet is compensated by the magnetic

pressure occurring due to supercurrent circulation on the surface of the super-

conductor.

4.3 Flux quantization

The quantum nature of the superconducting state manifests itself in quanti-

zation of magnetic ﬂux. One of the characteristics of the quantum world is the

quantization of a number of physical quantities, such as energy, spin, momen-

tum etc. So, they can take on only a discrete set of values. Since the super-

conducting state is the quantum state occurring on a macroscopic scale, some

physical quantities characterizing the superconducting state are quantized too.

Consider a bulk superconductor having a hole, as schematically shown in

Fig. 2.13. Assume that the magnetic ﬁeld H

was applied to the superconduc-

Basic properties of the superconducting state 43

Figure 2.13. Superconductor with a hole. The contour of integration C goes around the hole

through the interior of the superconductor.

tor at T>T

, parallel to the hole walls. Then the superconductor was cooled

down to T<T

. In the non-superconducting hole, some magnetic ﬂux will re-

main “frozen”, produced by the supercurrent generated at the internal surface

of the hole. Recalling that the order parameter of a conventional superconduc-

tor can be written in the form Ψ(r)=(n

/2)

1/2

iθ(r)

, where n

is the density

of superconducting electrons, and θ is the phase. In the superconductor with a

hole, the order parameter has to go through an integral number of oscillations

around the hole. The integral number of oscillations of Ψ explains why mag-

netic ﬂux inside the hole is quantized. Let us ﬁnd the value of this “frozen”

magnetic ﬂux.

First, we need to know the expression for a current-density vector opera-

tor in quantum mechanics. In classical mechanics, Hamilton’s equations are

expressed in terms of the canonical variables, p

. In the absence of mag-

netic ﬁeld and charge particles, the quantity p is the same as the ordinary or

kinematic momentum, p = mv. However, when a particle carries charge q

and moves in a magnetic ﬁeld H associated with the vector potential A, the

canonical and kinematic momenta are different, and related by

p = mv + qA, or mv = p − qA. (2.28)

In electrodynamics, the vector potential A is deﬁned as

H = ∇×A = curl A, with ∇·A = grad A =0. (2.29)

In quantum mechanics, the relation between the canonical and kinematic mo-

menta is maintained, but the canonical momentum is replaced by an operator:

p −→ −i¯h∇. In quantum mechanics, the ﬂow of particles characterized by a

wavefunction (order parameter) Ψ is described by a current density vector

J =

[(−i¯h∇Ψ)

∗

Ψ+Ψ

∗

(−i¯h∇Ψ)]. (2.30)