Mourachkine A. Room-Temperature Superconductivity

Подождите немного. Документ загружается.

14 ROOM-TEMPERATURE SUPERCONDUCTIVITY

4. Why the living matter is organic?

One may ask how does this question relate to the issue of room-temperature

superconductivity? In fact, the superconducting state and some biological pro-

cesses have, at least, one thing in common—they do not like the electron spin.

The prologue to this chapter may look unusual, and to better understand its

meaning here is a quote from the same book [19]: “From the physics point

of view, the general understanding of many biological processes is still very

limited. However, it is known that (i) in redox reactions occurring in liv-

ing organisms, electrons are transferred from one molecule to another in pairs

with opposite spins; and (ii) electron transport in the synthesis process of ATP

(adenosine triphosphate) molecules in conjugate membranes of mitochondria

and chloroplasts is realized by pairs, but not individually [9, 10]. Apparently,

in living tissues, electron transfer is preferable in pairs in which two electrons

are in a singlet state. ...

“At the Big Bang, spin was attached to what are now called the fermions in

order to create diversity of possible forms of the existence of matter. Seem-

ingly, in living tissues which appeared later, the spin of the electron became

rather an obstacle in the evolution of the living matter. In many biological

processes, in order to get rid of the electron spin, two electrons with opposite

spins are coupled, forming a composite boson with 2e charge and zero spin. It

happened that in inorganic solids two electrons, in some circumstances, can be

paired too. This state of matter, which is in fact an instability in solids, is now

called the superconducting state. Thus, the understanding of some biological

processes can lead to better understanding of the phenomenon of superconduc-

tivity in solids. This is particularly true in the case of high-T

superconductiv-

ity. Superconductivity does not occur in living tissues because it requires not

only the electron pairing but also the phase coherence among the pairs.”

Nevertheless, the superconducting-like state exists locally in complex or-

ganic molecules with conjugate bonds [23]. Figure 1.3 shows a few examples

of such molecules. Their main building blocks are carbon and hydrogen atoms.

The characteristic feature of these conjugated hydrocarbons is the presence of a

large number of π electrons. These collectivized electrons are in the ﬁeld of the

so-called σ electrons which are located close to the atomic nuclei and not much

different from the ordinary atomic electrons. At the same time, the π electrons

are not localized near any particular atom, and they can travel throughout the

entire molecular frame. This makes the molecule very similar to a metal. The

framework of atoms plays the role of a crystal lattice, while the π electrons that

of the conduction electrons. As an example, Figure 1.4 schematically shows

the formation of σ- and π-orbitals in ethene. It turns out, in fact, that the con-

jugated hydrocarbons with even number of carbon atoms are more than just

similar to a metal, but are actually small superconductors [23]. Experimen-

Introduction 15

(b)

(c)

(d)

(a)

Figure 1.3. Organic molecules with delocalized π electrons: (a) tetraphenylporphin; (b) ova-

lene; (c) hexabenzocoronene, and (d) coronene [23].

tally, conjugated hydrocarbons with even number of carbon atoms (thus, with

even number of π electrons) exhibit properties similar to those of a supercon-

ductor: the Meissner-like effect, zero resistivity and the presence of an energy

gap. The π electrons form bound pairs analogous to the Cooper pairs in an

ordinary superconductor. The pair correlation mechanism is principally due to

two effects: (i) the polarization of the σ electrons, and (ii) σ − π virtual elec-

tron transitions. However, if the number of π electrons is odd, the properties

of such conjugated hydrocarbons are different from those of a superconductor.

Thus, “the essential ﬂuidity of life agrees with the ﬂuidity of the electronic

cloud in conjugated molecules. Such systems may thus be considered as both

the cradle and the main backbone of life” [24]. At the end, I would like to

recall the prologue to this book: In order to create the living matter, Nature

-orbitals

hybrid

orbitals

-orbital

Figure 1.4. Formation of π- and σ-orbitals in ethene.

16 ROOM-TEMPERATURE SUPERCONDUCTIVITY

needed billions of years. This experience is unique, and we must learn from it.

Finally, aside from our problem of room-temperature superconductivity,

why, indeed, is the living matter (including us) organic? Could we exist being

made from, for example, B or N? The answer is no. Just by using common

sense and the periodic table of chemical elements (the Mendeleev table) it is

not difﬁcult to show that the element which we could be made from can only

be carbon. Only C can perform this function.

Chapter 2

BASIC PROPERTIES OF THE

SUPERCONDUCTING STATE

Any state of matter has its own speciﬁc characteristics and basic properties.

For example, viscosity is a characteristic of a liquid, and a liquid takes the

shape of a container which contains the liquid. The latter is one of the basic

properties of a liquid. As remarked in Chapter 1, the superconducting state is

a state of matter. Therefore, it has its own speciﬁc characteristics and basic

properties, and we need to know them before we discuss room-temperature

superconductivity. We also need to know why it occurs. What does cause

superconductivity?

In earlier textbooks on the physics of superconductivity, the description of

the superconducting state is based on the BCS theory, assuming that the BCS

model is the only possible mechanism of superconductivity. In fact, as we shall

see in the next chapter, all superconductors can be divided into three groups in

accordance with the mechanism of superconductivity in each compound. Con-

trary to this old tradition, the purpose of this chapter is to characterize the su-

perconducting state as whole, independently of any speciﬁc mechanism. Later,

in Chapters 5, 6 and 7, we shall separately consider characteristic features of

superconductivity in each group.

1. What is the superconducting state?

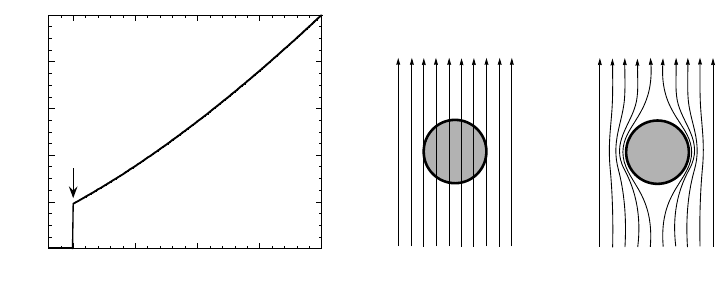
Superconductivity was discovered by Kamerlingh Onnes and his assistant

Gilles Holst in 1911: on measuring the electrical resistance of mercury at low

temperatures, they found that, at 4.2 K, it dropped abruptly to zero (see Fig.

1.1). Subsequent investigations have shown that this sudden transition to per-

fect conductivity is characteristic of a number of metals and alloys. However,

some metals never become superconducting. Bardeen, Cooper and Schrieffer

reported in 1957 the ﬁrst successful microscopic theory of superconductivity

18 ROOM-TEMPERATURE SUPERCONDUCTIVITY

ρ(Τ) / ρ(300 Κ)

T (K)

300

Figure 2.1. Temperature dependence of

electrical resistivity of a superconductor.

marks the transition to the supercon-

ducting state.

T > T

T < T

Figure 2.2. The Meissner effect: the ex-

pulsion of a weak, external magnetic ﬁeld

from the interior of a superconductor. The

ﬁeld is applied (a) at T>T

, and (b) at

T<T

(BCS theory). Despite the existence of the BCS theory, there are no com-

pletely reliable rules for predicting whether a metal will superconduct at low

temperature or not.

From a classical point of view, the superconducting state is characterized by

two distinctive properties: perfect electrical conductivity (ρ = 0) and perfect

diamagnetism (B = 0 inside the superconductor), as shown in Figs 2.1 and 2.2,

respectively. However, this deﬁnition of the superconducting state can soon be

changed because, as recently found in an unconventional organic superconduc-

tor, the applied magnetic ﬁeld induces superconductivity. Therefore, B =0

inside this organic superconductor (see Section 4.10).

2. Why does superconductivity occur?

At the Big Bang, Nature created two types of elementary particles: bosons

and fermions. Every elementary particle is either a boson or a fermion. This

is known as the quantum statistical postulate. Whether an elementary particle

is a boson or fermion is related to the magnitude of its spin (in units of ¯h).

Particles having an integer spin are bosons, while those with a half-integer

spin are fermions. Electrons are fermions with a spin of 1/2. According to

the Pauli exclusion principle no two electrons can occupy the same energy

state. At the same time, bosons can occupy the same state multiply. This is the

main difference between bosons and fermions. Thus, they conform to different

quantum statistics. Fermions obey the Fermi-Dirac statistics: for a system of

free fermions in equilibrium at temperature T , the probability of occupation of

Basic properties of the superconducting state 19

a level of energy E is given by the Fermi-Dirac distribution function:

(E) ≡

exp[(E −µ)/k

T ]+1

, (2.1)

where µ is the chemical potential (in metals, the chemical potential at low tem-

peratures is very close to the Fermi level), and k

is the Boltzmann constant.

Bosons obey the Bose-Einstein statistics: for a system of free bosons in equi-

librium, the probability of occupation of a level of energy E is given by the

Bose distribution function:

(E) ≡

exp[(E −µ)/k

T ] − 1

. (2.2)

For fermions, Nature had however created a “loophole”: under some cir-

cumstances, they can become bosons (but bosons can never be fermions). The

moment fermions become bosons, they switch the statistics which they are

obeying. As a consequence, the properties of the system are radically changed

at this moment. This is exactly what happens in a superconductor at criti-

cal temperature: two electrons, if there is a net attractive force acting between

them, form a pair which is already a boson with zero spin (or a spin equal to 1).

These electron pairs being in a phase can move in a crystal without friction. In

conventional superconductors, the pairing occurs in momentum space which is

reciprocal to real space. In fact, it is not important whether the electron pairing

occurs in momentum or, for example, real space. The most crucial circum-

stance for the electron pairing and, thus, for the onset of the superconducting

state, is that the net force acting between two electrons must be attractive. In a

superconductor, the electron pairs is usually called the Cooper pairs.

Are these electron pairs (composite bosons) really bosons? The answer is

yes. For example, atomic nuclei are composed of protons and neutrons (which

are fermions), and atoms are composed of nuclei and electrons. Thus, nuclei

and atoms are composite objects. It has been experimentally demonstrated

that they are indistinguishable quantum particles. Therefore, they are either

bosons or fermions (this depends on the total number of elementary fermions

in a composite particle). Two electrons, if there is an attraction between them,

indeed, represent a boson. If the attractive force disappears, the two electrons

will again behave as fermions do. As a matter of fact, all experimental and

theoretical studies of superconductivity are in a ﬁrst approximation reduced to

ﬁnding the origin of this attractive force.

It is important to note that the phenomenon of fermion pairing gives rise not

only to superconductivity, i.e. to the absence of electrical resistance in some

solid conductors, but also to some other peculiar correlated states of matter.

The latter ones can in a sense be considered as various manifestations of the

superconducting state in Nature. For example, the fermion pairing gives rise

20 ROOM-TEMPERATURE SUPERCONDUCTIVITY

to superﬂuidity. At 2.19 K, liquid

He undergoes a superﬂuid transition. Be-

low the transition temperature, liquid

He exhibits frictionless (zero viscosity)

ﬂow remarkably similar to supercurrents in a superconductor. The

He atoms

consisting of 2 protons, 2 neutrons and 2 electrons, are composite bosons, and

a ﬁnite fraction of them (about 7%) experience at 2.19 K (in fact, at 2.17 K)

the Bose-Einstein condensation which we shall discuss in Chapter 4.

The fermion pairing gives also rise to the “superconducting” state in nuclei

and neutron stars. The atomic nuclei are composed of protons and neutrons

which have a spin of 1/2. If the total number of protons and neutrons in a

nucleus is even, does the nucleus become superconducting? Yes and no. No,

because, in a nucleus, there is no sense in discussing the absence of electrical

resistivity—this concept has no meaning. Yes, because there are other indica-

tions of the “superconducting” state in nuclei having even number of protons

and neutrons. For example, nuclei having even and odd number of protons and

neutrons absorb radiation differently. In nuclei with even number of protons

and neutrons, the fermions are paired. As a consequence, the energy of an in-

coming photon must be equal to or greater than the binding energy of a bound

pair, otherwise, the radiation cannot be absorbed. Contrary to this, in nuclei

having odd number of protons and neutrons, there is an unpaired fermion left

over, which can absorb photons with much lower energy than that in the ﬁrst

case. Another indication of the fermion pairing in nuclei is provided by the

fact that the measured nuclear moments of inertia are considerably smaller

than the values calculated theoretically with the use of the noninteracting par-

ticle model. This effect is similar to that observed in superﬂuid helium. Thus,

the paired fermions in a nucleus form a Bose condensate similar to that in liq-

uid

He. The development of the superﬂuid model of the atomic nucleus has

predicted a large number of important results observed experimentally.

In neutron stars consisting almost entirely of neutrons, the neutron liquid

is in a state analogous to that in an atomic nucleus. Thus, in neutrons stars,

neutrons are paired. As we shall see below, superconductors have very low

heat capacity. Due to this property, neutron stars cool very rapidly. Another

indication of neutron pairing in neutron stars is the quantization of their angular

momentum (every neutron star or pulsar rotates about its axis). This effect is

similar to that in liquid helium. Generally speaking, the discreteness of any

physical quantity is the ﬁngerprint of the quantum world.

Undoubtedly, there are other manifestations of fermion pairing in Nature,

which we are not yet aware of. The phenomenon of superconductivity is only

one and, probably, the most spectacular exhibition of fermion pairing, occur-

ring in some solids.

It is worth noting that in spite of the fact that this “loophole” for fermions

was most likely created by Nature intentionally, one should however realize

that the occurrence of the superconducting state on a macroscale is rather Na-

Basic properties of the superconducting state 21

ture’s oversight, it is an anomaly (see the Introduction). The occurrence of the

superconducting state on a macroscale requires not only the electron pairing

but also the onset of long-range phase coherence. They are two different and

independent phenomena.

2.1 What causes superconductivity?

Superconductivity is not a universal phenomenon. It shows up in materials

in which the electron attraction overcomes the repulsion. What can cause the

occurrence of this attractive force in solids? In all known cases at the mo-

ment of writing, it is the interaction between electrons and the crystal lattice.

Thus, the electron-phonon interaction in solids is responsible for the electron

attraction, leading to the electron pairing. It turns out that the electron-electron

attraction provided by the lattice can overcome the electron-electron repulsion

caused by the Coulomb force, so, the net force acting between them can be

attractive.

3. Characteristics of the superconducting state

Before we discuss the basic properties of the superconducting state, itis nec-

essary, ﬁrst, to know its speciﬁc characteristics. Such a sequence will simplify

the understanding of this peculiar state of matter. Forinstance, in the aforemen-

tioned example, before studying a liquid, one must know what is the viscosity.

Of course, some characteristics of the superconducting state are identical to the

characteristics of the normal state. For example, the energy gap (see below) in

a superconductor is tied to the Fermi surface which is the typical characteris-

tic of a metal. In addition, a few characteristics such as the electron mass m,

the electron charge e, the Fermi velocity v

, the electron mean free path  and

so on, are simply indispensable for characterizing the superconducting state.

Also, one should bear in mind that, in a superconductor at any T>0, the vast

majority of conduction electrons remain normal.

3.1 Critical temperature

The phase transition from normal into the superconducting state is a second-

order transition, occurring at a temperature called the critical temperature T

shown in Fig. 2.2. The values of T

for some superconductors are given in

Tables 2.1 and 2.2.

The superconducting state requires the electron pairing and the onset of

long-range phase coherence, which in general occur at different temperatures.

is the temperature controlled by the onset of long-range phase order.

For every superconducting material, the critical temperature is exclusively

determined experimentally. At the moment of writing, there is no theoretical

formula for predicting the value of critical temperature in a given compound.

22 ROOM-TEMPERATURE SUPERCONDUCTIVITY

Table 2.1. Critical temperature T

, the penetration depth λ(0), the intrinsic coherence length

and the critical magnetic ﬁeld H

for some elemental superconductors

Element T

(K) λ(0) (A

◦

) ξ

◦

) H

(T )

Al 1.1 500 16000 0.01

Pb 7.2 390 830 0.08

Sn 3.7 510 2300 0.03

In 3.4 640 4400 0.03

Tl 2.4 920 - 0.02

Cd 0.56 1300 7600 0.003

There is even no rule for predicting whether a certain substance will undergo

the superconducting transition at low temperature or not. Actually, this is one

of the main problems in the ﬁeld of superconductivity—how to calculate the

value in different materials. If we could know how to estimate the T

value

for any speciﬁc material, there would be no need for this book. Stop reading

and think this over for a while—this is an important point.

This book does not provide a formula for estimating the value of T

for any

compound (this is in fact an impracticable task). Instead, this book presents an

analysis of experimental facts, which is further used to show a way in achieving

the goal, namely, T

 350 K.

It is necessary to note that, in the framework of the BCS theory, there is

in fact a formula for estimating the T

value (see Chapter 5); however, it is

a general formula which does not take into account any speciﬁc features of a

certain material.

Finally, one should remember that the critical temperature is a macroscopic

quantity, whilethe Cooper-pair wavefunction and the order parameter are quan-

tum ones.

3.2 Cooper-pair wavefunction

As discussed above, if in a solid, there is an attraction between two elec-

trons, they become coupled, forming a composite boson. The electron pairing

may occur in momentum or real space (see Chapter 4). Even if the lifetime of

these paired electrons is very short, ∼ 10

−12

–10

−15

s, nevertheless, they live

long enough, so that their effect on the properties of the system is almost the

same as that of bosons with the inﬁnite life-time.

In quantum mechanics, any particle is characterized by a wavefunction. So,

a Cooper pair is also characterized by a wavefunction ψ(r

−r

), where r

and

are the positions of each electron in real space, and the difference r

− r

is the relative coordinates. In Chapter 5, we shall see that in conventional

superconductors, the Cooper-pair net spin is zero, s

+ s

= 0, as well as the

Cooper-pair net momentum, k

+ k

= 0. Figure 2.3 schematically shows

Basic properties of the superconducting state 23

Figure 2.3. Schematic illustration of the Cooper-pair wavefunction in conventional supercon-

ductors. The diameter of a pair is around 100–1000 nm, and the wavelength is about 1 nm. So,

the diameter of a pair is in fact equal to hundreds of wavelengths (this sketch shows just a few).

The frequency of oscillations is of the order of 10

Hz (f =2E

/h).

the Cooper-pair wavefunction. The wavefunction ψ is a complex scalar having

an amplitude and a phase. By deﬁnition, the probability to ﬁnd a Cooper pair

in real space is given by ψ

∗

ψ, where ψ

∗

is the complex conjugate of ψ. The

probability distribution of a Cooper pair in relative coordinates is schematically

shown in Fig. 2.4.

∗

“Size” of a Cooper pair

Figure 2.4. Schematic representation of the probability distribution of a Cooper pair in rela-

tive coordinates. The maximum probability is located between two electrons bound by a net

attractive force.

3.3 Order parameter

The wavefunction of the superconducting condensate is called the order pa-

rameter. It is probably the most important parameter of the superconducting

state. As mentioned in the Introduction, the superconducting state is a quantum

state occurring on a macroscopic scale. This is the reason why the supercon-

ducting state is characterized by a single wavefunction Ψ(r). Any wavefunc-

tion has an amplitude and a phase, therefore, it can be presented as

Ψ(r)=|Ψ(r)|e

iθ(r)

, (2.3)

where θ(r) is the phase. The order parameter has the following properties: