Mourachkine A. Room-Temperature Superconductivity
Подождите немного. Документ загружается.

184 ROOM-TEMPERATURE SUPERCONDUCTIVITY
stripes located between charge stripes sets in at T
MO
. So, all these clusters
and matrix are spatially separated. Four, the real doping dependences T
MT
(p),
T
CO
(p), T
MO
(p) and T
pair
(p) are most likely not linear but quasi-linear. Five,
in the literature, there is discrepancy among phase diagrams inferred from dif-
ferent sets of experimental data. This is because the phase diagram of every
superconducting cuprate consists of several energy/temperature scales (at least,
seven) which have different origins. Since different experimental techniques
are sensitive to different types of correlations and have different resolutions
and different characteristic times, one can then understand why there is a dis-
crepancy among phase diagrams that can be found in the literature.
Finally, consider an interesting question: what type of clusters does the
T
c
(p) temperature scale originate from? One may immediately suggest that
the T
c
(p) temperature scale originates from the nanoscale clusters with vertical
stripes. The answer is yes and no. As was already emphasized, the phase dia-
gram in Fig. 6.11 is a superposition of different temperature scales originating
from three types of clusters (or matrix) depicted in Fig. 6.12. The spin-glass
temperature scale T
g
(p) has no direct relation with superconductivity; the other
temperature scales in Fig. 6.11 are presented in two plots, according to their
origin, as sketched in Fig. 6.13. One can see in Fig. 6.13a that the T
c
(p) tem-
perature scale is attributed mainly, but not solely, to the matrix (clusters) with
the local antiferromagnetic order. Why? The location of a quantum critical
point at p = 0.19, where magnetic fluctuations are the strongest, is the reason
for this. In the CuO
2
planes, the existence of the matrix (clusters) with local
antiferromagnetic order as well as the T
MT
temperature scale is determined by
the location of a quantum critical point. In a sense, the superconducting phase
is “attracted” at low temperature by a quantum critical point. Of course, the
charge-stripe fluctuations in clusters with vertical charge stripes generate spin
excitations that mediate the long-range phase coherence. However, in order
to propagate, the spin excitations must use a magnetic order, local or not. A
quantum critical point provides the occurrence of magnetic order.
3.5 Pseudogap
The pseudogap is a depletion of the density of states above the critical tem-
perature. Below a certain temperature, the cuprates do have a connected Fermi
surface that appears to be consistent with conventional band theory. Above T
c
,
the pseudogap dominates the normal-state low-energy excitations. The pseu-
dogap was observed for the first time in NMR measurements and therefore
mistakenly interpreted as a spin gap [8]. Later, ARPES, tunneling, Raman,
specific-heat and infrared measurements also provided evidence for a gap-like
structure in electronic excitation spectra. Thus, it became clear that the pseudo-
gap is not a spin gap but a gap to both spin and charge excitations; alternatively,
there are two spatially separated pseudogaps: one is a spin gap, and the second

Third group of superconductors: Mechanism of superconductivity 185
Temperature
0.05
0.19
0.27
p
T
MT
T
c
(a)
Temperature
0.05
0.27
p
T
CO
T
p
T
MO
T
c
(b)
QCP
Figure 6.13. Temperature scales from Fig. 6.11: (a) the T
MT
(p) scale is determined by a
quantum critical point (QCP) associated with antiferromagnetic phase, while (b) the T
CO
(p),
T
MO
(p) and T
pair
(p) scales originate from the striped phase shown in Fig. 6.2. The T
c
(p)
scale is a mutual temperature scale caused, first of all, by the quantum critical point and also by
spin excitations present in striped-phase clusters.
is a charge gap. The magnitude of pseudogap(s) is large in the underdoped
region and decreases as the doping level increases.
So, what is the pseudogap in cuprates? There is no straight answer to this
question because the answer depends upon the technique by which it was ob-
served and upon the temperature at which it was seen. Above T
c
, one may
observe four different gaps in the cuprates: (i) below T
CO
, a charge gap on the
charge stripes, ∆
cg
, (ii) below T
MT
, a gap having the magnetic origin, ∆
NMR
,
(iii) it is possible that a spin gap ∆
sg
sets in below T
MO
in hole-poor stripes in
the striped phase shown in Fig. 6.2, and (iv) below T
pair
, the pairing gap ∆
p
.
So, generally speaking, the pseudogap in the cuprates, ∆
pg
,is
∆
pg
=
∆
2
cg
+∆
2
NMR
+∆
2
sg
+∆
2
p
. (6.10)
However, there is no experimental technique able to detect all of these gaps
at once. The magnitudes of these four gaps are not affected much on cooling
through T
c
, but the pairing gap ∆
p
becomes a part of the superconducting gap,
∆
sc
=
∆
2
p
+∆
2
c
, predominant below T
c
. For example, in the case of ∆
cg
,
below T
c
there is a renormalization of low-energy excitations; thus, excitations
inside the charge gap. Let us consider this renormalization.
3.5.1 Charge gap on the stripes
The pseudogap which can be observed in tunneling and ARPES measure-
ments is a charge gap on charge stripes, manifesting itself in the form of wide
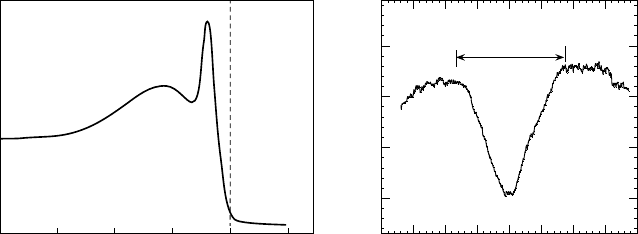
humps present in the spectra at high bias. Figure 6.14a shows an ARPES
186 ROOM-TEMPERATURE SUPERCONDUCTIVITY
0.8
1
-200 -100 0 100 200
Normalized dI/dV
Bias (mV)
T = 122 K
4∆
cg
(a) (b)
T
c
= 88 K
Bi2212
400
300
200
100
E
F
Binding Energy (meV)
Intensity
Bi2212
T < T
c
Figure 6.14. (a) ARPES spectrum obtained in a slightly overdoped Bi2212 single crystal with
T
c
=91KatT T
c
; and (b) Tunneling pseudogap in slightly overdoped Bi2212 obtained in
a SIS junction at T>T
c
(see references in [19]).
spectrum obtained below T
c
in Bi2212. In the plot, the position of main
quasiparticle peaks measures the magnitude of ∆
p
, while the hump at a bias
of V
hump
3∆
p
/e is caused by the charge gap on the stripes. The ratio
V
hump
/V
peak
3, inferred from either ARPES or superconductor-insulator-
normal metal (SIN) tunneling spectra, is independent of doping level. This
ratio is determined by the ratio ∆
cg
/∆
p
3 in Eq. (6.6).
In superconductor-insulator-superconductor (SIS) tunneling conductances,
however, the bias ratio is about V
hump
/V
peak
2 because the humps in SIS
conductances do not correspond directly to ∆
cg
but are a product of tunneling
between genuine humps and quasiparticle peaks. Thus at T T
c
, tunneling
dI(V )/dV and I(V ) characteristics as well as ARPES spectra consist of two
contributions caused by the superconducting condensate (bisolitons) and by
the charge gap on the stripes. In SIN conductances, these two contributions are
superimposed linearly while in SIS conductances, nonlinearly. This issue was
discussed in detail in Chapter 12 of [19].
Figure 6.14b depicts the pseudogap in a tunneling conductance obtained
by a break-junction technique in Bi2212 above T
c
. In the measurements, the
temperature of 122 K is above T
pair
120 K in slightly overdoped Bi2212
with p 0.19. The gap-like structure in tunneling conductances disappears
upon increasing the temperature.
Consider now the charge-gap renormalization at T
c
. Let us start with tun-
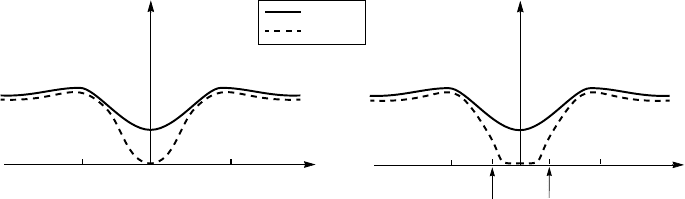
neling measurements. Figure 6.15a sketches the charge gap above and deep
below T
c
. Above the critical temperature, there are quasiparticle excitations
at the Fermi level (at zero bias in Fig. 6.15a). As the temperature is lowered
through T
c
, quasiparticle excitations at the Fermi level, thus inside the gap,
are renormalized: the charge gap deepens at low bias, as shown in Fig. 6.15a.
Third group of superconductors: Mechanism of superconductivity 187
However, the maximum magnitude of the gap, in a first approximation, is un-
changed. Analysis of ARPES data even suggests that a full gap opens up at
the Fermi level, as shown in Fig. 6.15b. The magnitude of this gap is slightly
smaller than the magnitude of ∆
p
, and its temperature dependence is reminis-
cent of the BCS temperature dependence (see references in [19]). If this is the
case, then the charge gap at T T
c
has an anisotropic s-wave symmetry with
an anisotropy ratio of about 3 because ∆
cg,min
≈ ∆
p
and ∆
cg,max
3∆
p
.
Thus, the ratio is ∆
cg,max
/∆
cg,min
≈ 3∆
p
/∆
p
= 3.
From Eqs. (6.5)–(6.7), the gap ratio 2∆
cg
/(k
B
T
CO
) 6 is sufficiently
large, indicating a strong coupling between the lattice and holes. As noted
above, the charge stripes represent self-trapped electronic states in the CuO
2
planes. In crystals, self-trapped states occur usually due to an interaction of
quasiparticles with acoustic phonons. The electron-phonon interaction in the
CuO
2
planes will be discussed separately.
Finally, it is worth to mention that in the ARPES spectrum shown in Fig.
6.14a, the dip that naturally occurs from a superposition of the quasiparticle
peak and the hump has no physical meaning. In ARPES and SIN-tunneling
spectra, this dip is situated at e|V |2∆
p
(p), while in SIS tunneling conduc-
tances, it appears at e|V |≈3∆
p
(p).
3.5.2 T
MT
(p) temperature scale
The T
MT
temperature scale shown in Fig. 6.11 manifests itself in resistivity,
NMR and specific-heat measurements. It originates from local antiferromag-
netic ordering in hole-poor matrix (clusters) depicted in Fig. 6.12. Therefore,
the energy scale related to the T
MT
temperature scale, ∆
NMR
, has also the
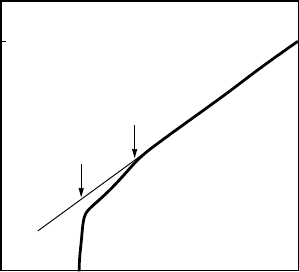
magnetic origin. Figure 6.16 illustrates how the temperature T
MT
is deter-
mined in resistivity measurements: T
MT
is the temperature at which, upon
cooling, the resistivity deviates from a linear temperature dependence.
(a)
V
dI/dV
−∆
cg
/e
∆
cg
/e
(b)
−∆
p
/e
∆
p
/e
0
V
dI/dV
−∆
cg
/e
∆
cg
/e
T > T
c
0
T < T
c
Figure 6.15. Gap on the charge stripes above and deep below T
c
, inferred from (a) tunneling
and (b) ARPES measurements (see references in [19]). In both plots, the solid lines are slightly
shifted up for clarity.
188 ROOM-TEMPERATURE SUPERCONDUCTIVITY
0
300
0
1
ρ
(T)/
ρ
(300)
Temperature (K)
T
MT
T
c
Figure 6.16. Pseudogap in resistivity measurements: T
MT
is the temperature at which the
resistivity deviates on cooling from a linear dependence.
Why does the resistivity drop at T
MT
? The temperature T
MT
is the onset
temperature of local antiferromagnetic order in either the insulating matrix, if
p 0.19, or insulating clusters, if p → 0.19. In nanoscale clusters with charge
stripes, holes can move easily along the stripes. To sustain electrical current
on a macroscopic scale, quasiparticles must tunnel through the insulating ma-
trix (clusters). It is mistakenly believed that an antiferromagnetic ordering
blocks electron transport. The opposite is true: electrons can tunnel through a
thin layer of NiO
2
ordered antiferromagnetically about five times easier than
through a thin layer of non-magnetic metal oxides [46]. This is why the tem-
perature dependence of in-plane resistivity in the cuprates has a kink at T
MT
:
the resistivity simply drops at T
MT
.
3.6 Soliton-like excitations on charge stripes
Depending on temperature, quasiparticles in superconducting cuprates are
soliton-like excitations or pairs of these excitations, observed experimentally
in tunneling measurements [16–19]. In the CuO
2
planes, the soliton-like ex-
citations appear on the charge stripes immediately after the formation of the
stripes, thus, somewhat below T
CO
. They become paired at T
pair
shown in the
phase diagram in Fig. 6.11. Consider first the elementary excitations; the pairs
will be discussed in the following subsection.
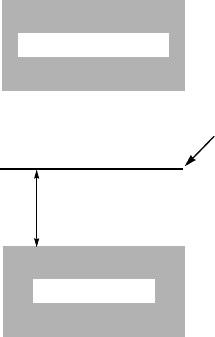
In the cuprates the soliton-like excitations propagate in the middle of the
charge gap present on the stripes, as depicted in Fig. 6.17. Since these exci-
tations have the quantum numbers of an electron, they are fermions. Then, a
question naturally rises: How can the fermions occupy the same energy level?
There are two possible explanations to this fact: Either there is the spin-charge
Third group of superconductors: Mechanism of superconductivity 189
separation on the stripes or, between T
CO
and T
pair
, there is no connected
Fermi surface in the cuprates yet. Theoretically the spin-charge separation is
indeed possible in one-dimensional systems, leading to the formation of the so-
called Luttinger liquid. However, an experimental verification of this hypothe-
sis, carried out in underdoped YBCO, showed that, within the resolution limits
of the experiment, there is no spin-charge separation in YBCO [47]. Hence, it
is most likely that, at T
pair
<T <T
CO
, there is no connected Fermi surface
in the cuprates. This means that, at high temperatures, the charge stripes in the
CuO
2
planes exist independently of each other. For example, in LSCO, upon
cooling the chemical potential literally jumps at about 250 K. Thus, if this is
the case, it is then possible that the soliton-like excitations become paired at
T
pair
because they are required to. When the Fermi surface in the cuprates be-
comes connected somewhat above T
pair
, the soliton-like excitations being at
the same energy level must either disappear, except for two, or be paired. The
paired quasiparticles are bosons, therefore, the Pauli exclusion principle is no
longer applicable to them.
What type of excitations can occur on the charge stripes in the cuprates?
Let us consider all possible excitations on a 2k
F
charge stripe sketched in Fig.
6.9. In the case of hole-doped cuprates, we are exclusively interested in the
stripe excitations with a charge of +|e|, where e is the electron charge. Figure
6.18 shows schematically three types of excitations on the 2k
F
charge stripes:
a soliton, a kink-up and a kink-down. In Fig. 6.18, the stripe excitations are
shown at rest; however, in reality, they are dynamic and propagate along the
stripes which themselves fluctuate in the CuO
2
planes. As suggested by Za-
valence band
conduction band
electrosoliton
∆
cg
Figure 6.17. Energy level of soliton-like excitations that reside on charge stripes in the CuO
2
planes at high temperatures. ∆
cg
is the magnitude of the charge gap on the stripes.

190 ROOM-TEMPERATURE SUPERCONDUCTIVITY
S
K
...
...
...
...
(a)
(b)
...
...
(c)
K
Figure 6.18. Sketch of three types of excitations on 2k
F
charge stripes, shown at rest: (a)
soliton; (b) kink-up, and (c) kink-down.
anen and co-workers, the kink-up and the kink-down may have different spin
orientations.
Such a description of soliton-like excitations in the cuprates is rather phe-
nomenological. In a first approximation, they can also be described mathemat-
ically in the framework of the Davydov theory of electrosolitons and bisoli-
tons for one-dimensional systems [3, 7, 9, 10]. Let us consider briefly the
electrosoliton model. As discussed in Chapter 1, solitons are nonlinear ex-
citations which are localized in space. In some systems, they represent self-
localized states (i.e. self-trapped states). In solids, if the particle-field inter-
action (electron-phonon coupling) is strong, both the particle wavefunction
and the lattice deformation will be localized. In the three-dimensional case,
this localized entity is known as a (Holstein) polaron and, in one dimension,
as a Davydov soliton (also known as an electrosoliton or polaronic soliton).
Their integrity is maintained owing to a dynamical balance between dispersion
(exchange inter-site interaction) and nonlinearity (electron-phonon coupling).
Figure 6.19 schematically shows a self-trapped state of a particle (small po-
laron or Davydov soliton). In a self-trapped state, both the particle wavefunc-
tion and the lattice deformation are localized.
Particle wave-function
Potential well
Figure 6.19. Sketch of a self-trapped state: a particle (electron or hole) with a given wave-
function deforms the lattice inducing a potential well which in turn traps the particle.

Third group of superconductors: Mechanism of superconductivity 191
To describe the self-focusing phenomena, the nonlinear Schro¨dinger (NLS)
equation is used,
i¯h
∂
∂t
+
¯h
2
2m
∂
2
∂x
2
+ G|ψ(x, t)|
2
ψ(x, t)=0. (6.11)
The equation is written in the long-wave approximation when the excitation
wavelength λ is much larger than the characteristic dimension of discreteness
in the system, i.e. under the condition ka =2πa/λ 1. The equation
describes the complex field ψ(x, t) with self-interaction. The function |ψ|
2
determines the position of a quasiparticle of mass m. The second term in the
NLS equation is responsible for dispersion, and the third one for nonlinearity.
The coefficient G characterizes the intensity of nonlinearity.
When the nonlinearity is absent (G = 0), the NLS equation has solutions in
the form of plane waves,
ψ(x, t)=Φ
0
exp[i(ka − ω(k)t)], (6.12)
with the square dispersion law ω(k)=¯hk
2
/2m. With nonlinearity (G = 0)
in the system having a translational invariance, the excited states move with
constant velocity v. Therefore, it is convenient to study solutions of the NLS
equation in the reference frame
ζ =(x − vt)/a, (6.13)
moving with constant velocity. In this reference frame the NLS equation has
solutions in the form of a complex function
ψ(x, t)=Φ(ζ) exp[i(kx − ωt)],k= mv/¯h, (6.14)
where the function Φ(ζ) is real.
The self-trapping effect occurs when two linear systems interact with one
another. Consider an excesselectron in a quasi-one-dimensionalatomic (molec-
ular) chain. If neutral atoms (molecules) are rigidly fixed in periodically ar-
ranged sites na of a one-dimensional chain, then due to the translational in-
variance of the system, the lowest energy states of an excess electron are deter-
mined by the conduction band. The latter is caused by the electron collectiviza-
tion. In the continuum approximation, the influence of a periodic potential is
taken into account by replacing the electron mass m
e
by the effective mass
m =¯h
2
/(2a
2
J) which is inversely proportional to the exchange interaction
energy J that characterizes the electron jump from one node site into another.
In this approximation, the electron motion along an ideal chain corresponds to
the free motion of a quasiparticle with an effective mass m and the electron
charge.

192 ROOM-TEMPERATURE SUPERCONDUCTIVITY
Taking into account small displacements of molecules of mass M ( m)
from their periodic equilibrium positions, there arises the short-range defor-
mation interaction of quasiparticles with these displacements. When the defor-
mation interaction is rather strong, the quasiparticle is self-localized. The local
displacement caused by a quasiparticle manifests itself as a potential well that
contains the particle, as schematically shown in Fig. 6.19. In turn, the quasi-
particle deepens the well.
A self-trapped state can be described by two coupled differential equations
for the field ψ(x, t) that determines the position of a quasiparticle, and the field
ρ(x, t) that characterizes a local deformation of the chain and determines the
decrease in the relative distance a → a − ρ(x, t) between molecules of the
chain,
i¯h
∂
∂t
+
¯h
2
2m
∂
2
∂x
2
+ σρ(x, t)
ψ(x, t)=0, (6.15)
∂
2
∂t
2
− c
2
0
∂
2
∂x
2
ρ(x, t) −
a
2
σ
M
∂
2
∂x
2
|ψ(x, t)|
2
=0. (6.16)
The first equation characterizes the motion of a quasiparticle in the local de-
formation potential U = −σρ(x, t). The second equation determines the field
of a local deformation caused by a quasiparticle. The two equations are con-
nected through the parameter σ of the interaction between a quasiparticle and
a local deformation. The velocity c
0
= a
k/M is the longitudinal sound ve-
locity in the chain with elasticity coefficient k. In the case of one quasiparticle
in the chain, the function ψ(x, t) is normalized by
1
a
∞
−∞
|ψ(x, t)|
2
dx =1. (6.17)
In the reference frame ζ =(x −vt)/a moving with constant velocity v, the
following equality ∂ρ(x, t)/∂t = −v/a×∂ρ/∂ζ holds. Then, the solution for
ρ(x, t) has the form
ρ(x, t)=
σ
k(1 − s
2
)
|ψ(x, t)|
2
, if s
2
= v
2
/c
2
0
1. (6.18)
Substituting the expression for ρ(x, t) into Eq. (6.15), we obtain the follow-
ing nonlinear equation for the function ψ(x, t),
i¯h
∂
∂t
+
¯h
2
2m
∂
2
∂x
2
+2gJ|ψ(x, t)|
2
ψ(x, t)=0. (6.19)
where
g ≡
σ
2
2k(1 − s
2
)J
(6.20)

Third group of superconductors: Mechanism of superconductivity 193
is the dimensionless parameter of the interaction of a quasiparticle with local
deformation. Substituting the function
ψ(x, t)=Φ(ζ) exp[i(kx − ωt)],k= mv/¯h (6.21)
into Eq. (6.19) we get the equation
[¯hω −
1
2
mv
2
− J
∂
2
∂ζ
2
+2gJΦ
2
(ζ)]Φ(ζ)=0, (6.22)
for the amplitude function Φ(ζ) normalized by
Φ
2
(ζ)dζ =1. The solution
of this equation is
Φ(ζ)=
1
2
√
g × sech(gζ/2), (6.23)
with the dispersion law
¯hω =
1
2
mv
2
−
1
8
g
2
J. (6.24)
The last term in Eq. (6.24) determines the binding energy of the particle and
the chain deformation produced by the particle itself. According to Eq. (6.23),
the quasiparticle is localized in a moving reference frame
∆ζ =2π/g, (6.25)
as shown in Fig. 6.20. In this region, the field localization is characterized by
the function
ρ(ζ)=
gσ
4k(1 − s
2
)
sech
2
(gζ/2). (6.26)
The following energy is necessary for the deformation:
W =
1
2
k(1 + s
2
)
ρ
2
(ζ)dζ =
1
24
g
2
J(1 + s
2
). (6.27)
ζ
Φ
2
(
ζ
)
2
π
/
g
Figure 6.20. Size of a self-trapped soliton is about 2π/g (compare with Fig. 2.4).
