Mourachkine A. Room-Temperature Superconductivity

Подождите немного. Документ загружается.

154 ROOM-TEMPERATURE SUPERCONDUCTIVITY

3.5 Density of states of elementary excitations

The lower part of the elementary excitation spectrum of a superconductor is

depicted in Fig. 5.8. By combining the two equations, Eqs. (5.11) and (5.30),

we have



+∆









¯h

−

¯h



+∆

. (5.38)

This dependence of E

on k is illustrated in Fig. 5.9a. As one can see from this

plot and Fig. 5.8, the energy levels of elementary excitations become denser

at E

→ ∆

. In other words, the density of states near the Fermi level is the

highest.

∆

(a)

N(0)

(b)

∆

Figure 5.9. (a) Spectrum ofelementary excitations of asuperconductor, E

(see also Fig. 5.8),

and (b) its density of states N

at T = 0.

In a superconductor, the density of states is

N(E)=N(ε)

dε

= N(ε)

∆(T )



− ∆

(T )

, (5.39)

where N(ε) is the density of states of a superconductor in the normal state.

The density of states N(E) diverges at E → ∆

, as shown in Fig. 5.9b.

Figure 5.9b presents the density of states of a superconductor at T =0.At

ﬁnite temperatures 0 <T <T

, however, the density of states does not diverge

at E → ∆

because, at 0 <T, there are always excitations inside the gap, as

illustrated in Fig. 5.10. This effect can directly be observed in tunneling mea-

surements. It is worth noting that, the tunneling conductances dI(V )/dV ob-

tained in a superconductor-insulator-normal metal (SIN) junction corresponds

directly to the density of states of a superconductor if normalized to a normal-

state conductance G

[thus, to N(ε)]. The current-voltage tunneling character-

istics for a conventional superconductor are shown in Fig. 2.20. The conduc-

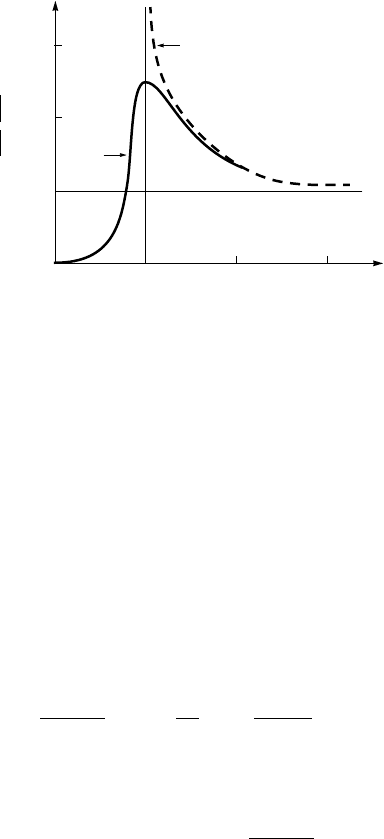
First group of superconductors: Mechanism of superconductivity 155

eV/

∆

T = 0

T > 0

Figure 5.10. Tunneling dI(V )/dV characteristic for a SIN junction at T>0. The dashed

line is the density of states of a superconductor at zero temperature (see Fig. 5.9b). G

is the

normal-state conductance.

tances measured in a superconductor-insulator-superconductor (SIS) tunneling

junction are proportional to the convolution of the density-of-states function of

a superconductor with itself.

3.6 Critical temperature

In the framework of the BCS theory, one can derive an expression for the

critical temperature. At T = T

, the gap is ∆(T

)=0. Then, replacing T in

Eq. (5.35) with T

and setting ∆(T )=0 yields an equation with respect to T

N(0)V

¯hω



dε

tanh

. (5.40)

Carrying out this integration, one gets

=1.14¯hω

exp



−

N(0)V



. (5.41)

Taking Eq. (5.37) into account, we have

2∆

=3.52k

. (5.42)

The last two relations are in good quantitative agreement with numerous ex-

periments. Moreover, Equation (5.41) provides an explanation for the isotope

effect (see Chapter 2): since the Debye frequency varies as ω

∝ M

−1/2

where M is the isotope mass, one immediately obtains from Eq. (5.41) that

the product T

1/2

is constant for a given superconductor.

156 ROOM-TEMPERATURE SUPERCONDUCTIVITY

3.7 Condensation energy

Here we calculate the condensation energy of the superconducting state at

T = 0, i.e. the difference in energy between the superconducting and normal

states:

W ≡ E

− E

=(E

kin

− E

kin

)+(E

pot

− E

pot

), (5.43)

where E

kin

and E

pot

are respectively the kinetic and potential energies. In the

normal state at T = 0, all states below the Fermi level are completely occupied

and, therefore, E

pot

= 0 and

kin



k<k

2ε

. (5.44)

Here the coefﬁcient 2 appears because the sum is taken over pairs of states

(k, −k). Then, taking into account that, at T = 0, f

= 0, and using Eq.

(5.24), the difference of kinetic energies is

kin

− E

kin



k<k

− 1)+2



k>k

. (5.45)

Using Eqs. (5.30), (5.31) and (5.37), one can easily transform Eq. (5.45) into

kin

− E

kin

= N(0)∆



N(0)V

−

(1 − e

−2/N (0)V

)



. (5.46)

Similarly, the potential energy of the superconducting state from Eq. (5.25) at

T =0is

pot

= E

= −

∆

. (5.47)

Then, the condensation energy is the sum of the last two equations:

W = −

N(0)∆



1 − e

−2/N (0)V



−

N(0)∆

if N(0)V  1. (5.48)

Since N(0)  N/E

, where N is the total number of free conduction elec-

trons, then the condensation energy per electron is about ∆

/(2E

). A similar

result was obtained in Chapter 2 by using common sense. Also in Chapter 2,

we established that the difference in free energy between the superconducting

and normal state equals H

/8π, where H

is the thermodynamic critical ﬁeld.

It then follows that at T =0

8π

N(0)∆

. (5.49)

From Eq. (2.20), H

(T ) varies with temperature as [1−(T/T

)

].AsT → T

this dependence becomes linear with T : H

∝ (T

− T ). As a consequence,

from Eq. (5.49), ∆(T ) varies with temperature at T → T

as (T

− T )

1/2

First group of superconductors: Mechanism of superconductivity 157

3.8 Coherence length

As deﬁned in Chapter 2, the coherence length ξ

is determined by varia-

tions of the order parameter Ψ(r), whilst the Cooper-pair size ξ is related to

the wavefunction of a Cooper pair, ψ(r). Furthermore, the coherence length

depends on temperature, ξ

(T ), while the Cooper-pair size is temperature-

independent. Since the order parameter in conventional superconductors is a

“magniﬁed” version of Cooper-pair wavefunctions, the values of coherence

length and Cooper-pair size in conventional superconductors coincide at T =

0: ξ

(0) = ξ(0) = ξ

The superconducting ground state can be represented by the distribution of

electron pairs in momentum space given by the function v

. The sketch of the

dependence of v

on k is shown in Fig 5.7. In this plot, one can see that large

variations of v

at T = 0 can occur only within the region

∆k ∼ k

2∆

, (5.50)

where E

=¯h

/2m is the Fermi energy. Then in real space, large vari-

ations of the order parameter of the ground state can be expected within the

interval ∆x deﬁned by the uncertainty relation

∆x∆k ∼ 1. (5.51)

Then, it follows that

∆x ∼

2∆

¯h

¯hp

4m∆

¯hv

4∆

, (5.52)

where p

and v

are respectively the electron momentum and velocity on the

Fermi surface. By deﬁnition, ∆x is the coherence length at T = 0, thus, the

intrinsic coherence length, ξ

≡ ∆x. A rigorous calculation yields

¯hv

π∆

. (5.53)

The difference between the two expressions is only in the numerical coefﬁcient

of π/4  0.785. As mentioned above, ξ

is also the size of the Cooper pairs at

T =0.

The estimation of ξ

for a metallic superconductor, made in Chapter 2,

yielded ξ

 3×10

◦

. The values of the intrinsic coherence length in conven-

tional superconductors can be found in Table 2.1. In spite of the fact that two

electrons in a Cooper pair in metallic superconductors are far apart from each

other, the other Cooper pairs are only a few tens of A

◦

away, as shown schemati-

cally in Fig. 4.1. Such a high concentration of the Cooper pairs in conventional

superconductors automatically leads to the onset of phase coherence.

158 ROOM-TEMPERATURE SUPERCONDUCTIVITY

3.9 Speciﬁc-heat jump

As discussed in Chapter 2, the appearance of the superconducting state is

accompanied by quite drastic changes in both the thermodynamic equilibrium

and thermal properties of a superconductor. The normal–superconducting tran-

sition is a second-order phase transition accompanied by a jump in heat capac-

ity. On cooling, the heat capacity of a superconductor has a discontinuous

jump at T

and then falls exponentially to zero, as illustrated in Fig. 2.23. In

the framework of the BCS theory, the value of this jump in heat capacity equals

β = 1.43, as speciﬁed by Eq. (2.54). Experimentally, the value of the jump in

speciﬁc heat in conventional superconductors with a strong electron-phonon

coupling can be much larger than 1.43.

3.10 Relation between the BCS and Ginzburg-Landau

theory

The Ginzburg-Landau theory of the superconducting state, which was dis-

cussed in Chapter 2, is phenomenological. Soon after the development of

the BCS theory, Gor’kov showed that the two theories—microscopic BCS

and phenomenological Ginzburg-Landau—are basically the same at T → T

However, the relation between the BCS and Ginzburg-Landau theory differs in

the so-called clean and dirty limits. To recall, the case when the mean electron

free path is larger than the Cooper-pair size,   ξ, is known as the clean

limit. In the dirty limit,   ξ. In what follows, all quantities corresponding to

“clean” superconductors will be labeled with an index “cl” and those to “dirty”

superconductors with an index “d”.

First of all, the energy-gap function in the BCS theory, ∆(r), is proportional

to the order parameter Ψ(r) in the Ginzburg-Landau theory at T → T

(r)=



7mv

N(0)

2π

ζ(3)



1/2

∆(r), (5.54)

(r)=



πmv

N(0)l

12¯hk



1/2

∆(r), (5.55)

where ζ(3)  1.202 is the Riemann function. The temperature dependence of

the energy gap at T → T

∆(T )  3.06 k



1 −



1/2

. (5.56)

The temperature dependences of the coherence length and magnetic penetra-

tion depth in the two limits are

GL,cl

=0.74 ξ



1 −



1/2

, (5.57)

First group of superconductors: Mechanism of superconductivity 159

GL,d

=0.85 (ξ

1/2



1 −



1/2

, (5.58)

λ(0)

√



1 −



1/2

, (5.59)

=0.615 λ(0)





1/2



1 −



1/2

, (5.60)

where ξ

is the intrinsic coherence length deﬁned in Eqs. (5.53) and (2.15),

and

(0) ≡

8πe

N(0)

. (5.61)

The coefﬁcients α and β in the Ginzburg-Landau theory can be expressed

in terms of ξ

and λ(0) as

= −1.83

¯h

2mξ



1 −



1/2

, (5.62)

= −1.36

¯h

2mξ



1 −



1/2

, (5.63)

0.35

N(0)



¯h

2mξ



, (5.64)

0.2

N(0)



¯h

2mξ



. (5.65)

Finally, the Ginzburg-Landau parameter k in these two limits is

=0.96

λ(0)

and k

=0.725

λ(0)

. (5.66)

4. Extensions of the BCS theory

As is natural with a development of such importance, the appearance of the

original paper by Bardeen, Cooper and Schrieffer was followed rapidly by a

number of papers giving reformulation of the calculations and some correc-

tions to the original results. Several of these reformulations and corrections

proved important in the later development.

4.1 Critical temperature

Here we discuss an important correction to the critical temperature obtained

for the case of strong electron-phonon coupling. For convenience, we intro-

duce a new parameter λ = N(0)V called the electron-phonon coupling con-

160 ROOM-TEMPERATURE SUPERCONDUCTIVITY

stant (not to be confused with the penetration depth). In the weak-coupling

limit, i.e. when λ  1, the inﬂuence of the Coulomb interaction on T

Eq. (5.41) can be taking into account by introducing the Coulomb pseudo-

potential:

=1.14¯hω

exp



−

λ − µ

∗



, (5.67)

where µ

∗

is N(0) times the Coulomb pseudo-potential. Later, McMillan ex-

tended this result for the case of strong-coupling superconductors, and obtained

1.45

exp



−

1.04(1 + λ)

λ − µ

∗

(1+0.62λ)



, (5.68)

where Θ is the Debye temperature. So, when the Coulomb interaction is taken

into account, the isotope-mass dependence of the Debye frequency appearing

in µ

∗

modiﬁes the isotope effect, and thus explains the deviation of the isotope

effect in some superconductors from the ideal value of 0.5 (see Table 2.3).

In BCS-McMillan’s expression for T

, the Debye temperature Θ occurs not

only in the pre-exponential factor in Eq. (5.68), but also in the electron-phonon

coupling constant λ which can be presented as λ ≈ C/Mω

, where C is a

constant for a given class of materials, M is the isotope mass, and ω

 is the

mean-square average phonon frequency, and ω

∝Θ. As a consequence,

in BCS-type superconductors, T

increases as Θ decreases. In other words,

increases with lattice softening. This, however, is not the case for high-T

superconductors (copper oxides) in which T

increases with lattice stiffening

(see Fig. 6.29), thus, contrary to the case of conventional superconductors.

This fact clearly indicates that the mechanism of superconductivity in high-T

superconductors, which will be discussed in the next chapter, is not of the BCS

type.

4.2 Strength of the electron-phonon interaction

The electron-phonon coupling constant λ in Eq. (5.68) can be determined

experimentally. In a given material, the strength of the electron-phonon in-

teraction depends on the function α

(ω)F (ω), where F (ω) is the density of

states of lattice vibrations (the phonon spectrum); α

(ω) describes the interac-

tion between the electrons and the lattice, and ω is the phonon frequency. The

spectral function α

(ω)F (ω) is the parameter of the electron-phonon interac-

tion in the Eliashberg equations, and if this function is known explicitly, one

can calculate the coupling constant λ with the help of the following relation

λ =2



(ω)F (ω)

dω

. (5.69)

The phonon spectrum F (ω) can be determined by inelastic neutron scat-

tering. The product α

(ω)F (ω) can be obtained in tunneling measurements.

First group of superconductors: Mechanism of superconductivity 161

A comparison of experimental data obtained by these two different techniques

revealsin many superconducting materials a remarkable agreement of the spec-

tral features. The function α(ω) can be determined explicitly from these data,

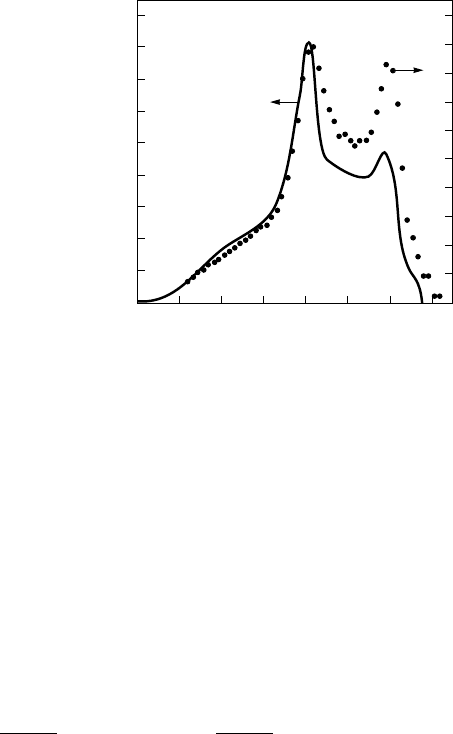
which is usually smooth relative to F (ω). As an example, Figure 5.11 shows

the phonon spectrum F (ω) and the function α

(ω)F (ω) for Nb, obtained by

neutron and tunneling spectroscopies, respectively. In Fig. 5.11, one can see

that there is good agreement between the two spectra. It is worth to mention

that the phonon spectrum in metals often has two peaks, as that in Fig. 5.11.

These peaks originate from longitudinal and transverse phonons.

)

0.2

0.4

0.6

0.8

0.1

0.08

0.06

0.04

0.02

(ω)

) (meV)

(meV)

Figure 5.11. Tunneling and neutron spectroscopic data for Nb (taken from [19]).

4.3 Tunneling

As we already know, tunneling dI(V )/dV characteristics obtained in an

SIN junction correspond to the density of states of quasiparticle excitations in

a superconductor. Let us derive this result. Assuming that the normal metal has

a constant density of states near the Fermi level and the transmission of the bar-

rier (insulator) is independent of energy, the tunneling conductance dI(V )/dV

is proportional to the density of states of the superconductor, broadened by the

Fermi function f(E,T) = [exp(E/k

T )+1]

−1

. Thus, at low temperature,

dI(V )

∝

+∞



−∞

(E)



−

∂

∂(eV )

f(E + eV, T )



∼

(eV ), (5.70)

where V is the bias; N

(E) is the quasiparticle density of states in a supercon-

ductor, and the energy E is measured from the Fermi level of a superconductor.

162 ROOM-TEMPERATURE SUPERCONDUCTIVITY

So, the differential conductance at negative (positive) voltage reﬂects the den-

sity of states below (above) the Fermi level E

In order to smooth the gap-related structures in the density of states N

shown in Fig. 5.10 at T → 0, a phenomenological smearing parameter Γ was

introduced, which accounts for a lifetime broadening of quasiparticles (Γ=

¯h/τ , where τ is the lifetime of quasiparticle excitations). The energy E in the

density-of-state function is replaced by E −iΓ as

(E,Γ) ∝ Re





E −iΓ



(E −iΓ)

− ∆

(k)



, (5.71)

where, in the general case, the energy gap ∆(k) is k-dependent. (In a two-

dimensional case, the integration is reduced to integrating over the in-plane

angle 0 ≤ θ<2π.)

In SIN tunneling junctions of conventional superconductors, there is good

agreement between the theory and experiment. However, for SIS-junction

characteristics, the correspondence between the smoothed BCS density of states

and experimental data is poor. This issue was raised for the ﬁrst time elsewhere

[19].

4.4 Effect of impurities on T

How do magnetic and non-magnetic impurities affect the critical temper-

ature in conventional superconductors? It turns out that, in superconductors

described by the BCS theory, non-magnetic impurities do not alter T

much,

whereas magnetic impurities drastically suppress the superconducting transi-

tion temperature.

The effect of non-magnetic impurities on T

was ﬁrst explained by Ander-

son in his theorem. In the normal state, the electrons may be described by wave

functions φ

n ↑

(r) and φ

n ↓

(r), where φ

is supposed to include the effects of

the impurity scattering. The quantum number n replaces the wave number k

we used for the pure metal. The Cooper pairs in the pure metal is composed

of the states (k, ↑) and (−k, ↓). The latter state is in fact the former one but

with momentum and current reversed in time. Anderson argued that, in the im-

pure metal, one should equally pair time-reversed states, namely, φ

n ↑

(r) and

∗

n ↓

(r): the complex conjugate φ

∗

n ↓

is the time reverse of φ

n ↑

just as e

−ik·r

the time reverse of e

ik·r

. With non-magnetic impurities, φ

∗

and φ

have the

same energy, and all the BCS calculations go through unmodiﬁed. In fact, the

impurity scattering washes out the effects of Fermi-surface anisotropy, so that

the BCS results apply rather better to alloys than to pure metals. Experimen-

tally, when non-magnetic impurities are added to a pure superconductor, the

critical temperature ﬁrst drops sharply and then varies only slowly as a func-

tion of the impurity concentration. The ﬁrst drop is related to the destruction

First group of superconductors: Mechanism of superconductivity 163

of anisotropy effects, and the subsequent slow change is caused by a change in

N(0).

In the case of magnetic impurities, φ

∗

and φ

have different energies. As

a consequence, this leads to a difference in energy between the two electrons

in a Cooper pair. When the mean value of this energy difference exceeds the

binding energy of the pairs, the electron pairing and, thus, the superconducting

state, can no longer occur.

The effect of suppression of the superconducting state by magnetic and non-

magnetic impurities is always used to determine the nature of the electron-

electron attraction in superconducting materials. For example, the effect of

impurities on T

in superconductors in which superconductivity is mediated

by magnetic ﬂuctuations should be opposite to that in conventional supercon-

ductors.

4.5 High-frequency residual losses

The vanishing of the dc resistance is the most striking feature of the super-

conducting state. However, the losses in a superconductor are non-zero for an

ac current which ﬂows in a thin surface layer having a thickness of λ (pen-

etration depth). The surface resistance depends on the frequency ω of an ac

current (or electromagnetic ﬁeld), as well as on the temperature and the energy

gap of a superconductor. At microwave frequencies and at temperatures less

than half the transition temperature, the surface resistance has the following

approximate BCS form:

(T,ω)=

Cω

−∆/k

+ R

(ω), (5.72)

where C is a constant that depends on the penetration depth in the material,

and R

is the residual resistance. Although it is not entirely clear where the

residual losses originate, it has been determined experimentally that trapped

ﬂux and impurities are principal causes. An additional source of the residual

losses can be imperfection of the surface of a superconductor, which may not

be perfectly ﬂat or contains non-superconducting regions (for example, oxides

etc.). Nevertheless, in conventional superconductors, the residual losses which

are determined by R

are small in comparison, for example, with those in

high-T

superconductors.