Mourachkine A. Room-Temperature Superconductivity

Подождите немного. Документ загружается.

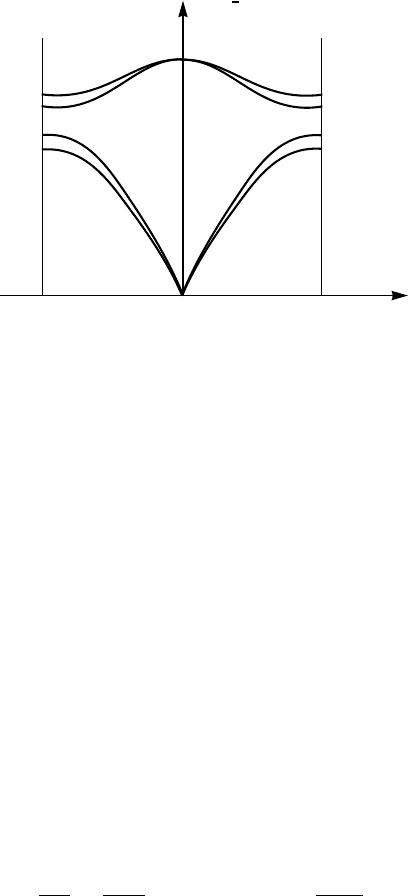
144 ROOM-TEMPERATURE SUPERCONDUCTIVITY

optical

−π/2

π/2

acoustic

Figure 5.3. Vibration frequencies of diatomic chain shown in Fig. 5.2 (L = longitudinal and

T = transverse).

the same volume in k-space. The Debye temperature Θ is deﬁned by

Θ=¯hω

, (5.1)

where ω

is the phonon frequency at the edge of the Debye sphere. Thus, k

(or ¯hω

) is the energy of the highest-energy phonon in the Debye sphere.

Let us go back to our electrons shown in Fig. 5.1. To enable an electron to

scatter from the state k

into the state k



, the latter must be free (in accordance

with the Pauli exclusion principle). This is possible only in the vicinity of

the Fermi surface which is represented in momentum space by a sphere of

radius k

, as shown in Fig. 5.4. Now we are ready to formulate the law of

phonon-mediated interaction between electrons which forms the foundation of

the BCS theory: Electrons with energies that differ from the Fermi energy by

no more than ¯hω

are attracted to each other. Thus, in the BCS model, only

those electrons that occupy the states within a narrow spherical layer near the

Fermi surface experience mutual attraction. The thickness of the layer 2∆k is

determined by the Debye energy:

∆k

∼

¯hω

, where E

¯h

, (5.2)

and m is the electron mass. As we shall see, the attraction is greatest for

electrons with opposite spins (s

= −s

) and equal and opposite wave vectors

= −k

The electron-electron attraction mediated by the background crystal lattice

can crudely be pictured as follows. An electron tends to create a slight distor-

tion of the elastic lattice as it moves because of the Coulomb attraction between

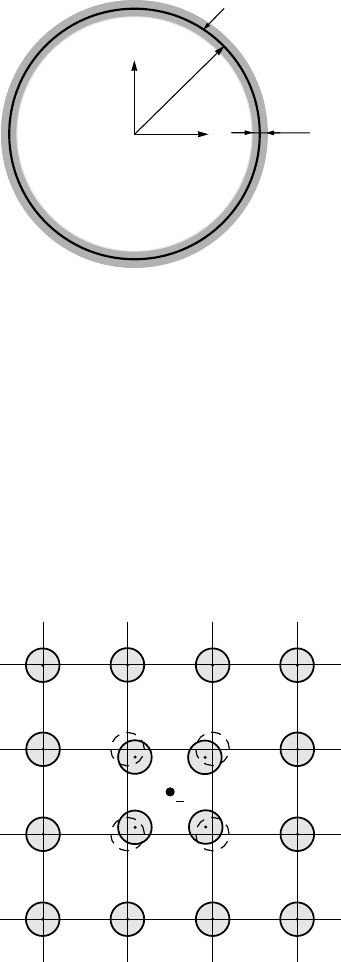
First group of superconductors: Mechanism of superconductivity 145

Fermi surface

2∆

Figure 5.4. In the BCS picture, only the electrons within the 2∆k layer near the Fermi surface

interact via phonons.

the negatively charged electron and the positively charged lattice, as illustrated

in Fig. 5.5. If the distortion persists for a brief time (retardation), a second

passing electron will feel the distortion and will be affected by it. Under cer-

tain circumstances, this can give rise to a weak indirect attractive interaction

between the two electrons which may more than compensate their Coulomb

repulsion. Thus, as shown in Fig. 5.5, the process of electron pairing in con-

ventional superconductors is local in space, but non-local in time.

Figure 5.5. Polarization of a lattice near a moving electron, which in turn attracts another

electron.

146 ROOM-TEMPERATURE SUPERCONDUCTIVITY

3. Main results of the BCS theory

The main idea of the BCS theory is based on the Cooper work. In 1956,

Cooper showed that two electrons with an attractive interaction can bind to-

gether in the momentum space to form a bound pair, if they are in the presence

of a high-density ﬂuid of other electrons, no matter how weak the interaction

is. This bound state of two electrons is today known as the Cooper pair.

3.1 Instability of the Fermi surface in the presence of

attractive interaction between electrons

Let us consider two electrons in a metal, added at the Fermi surface. In the

absence of interactions, their wavefunction can be written as

ψ(r

, r

)=e

i(k

)

i[q(r

)+k(r

−r

)]

(5.3)

where

q =

+ k

), (5.4)

k =

− k

In the center of mass, q =0. Then, in the presence of an interaction between

electrons (assumed attractive), the wavefunction can be presented as

ψ(r

, r



g(k)e

ik(r

−r

)

, (5.5)

where |g(k)|

is the probability of ﬁnding one electron with momentum k and

the other one with momentum −k. Of course,

g(k) ≡ 0 for |k| < |k

|, (5.6)

because all the electronic states |k| < |k

| are completely ﬁlled with electrons

and, in accordance with the Pauli exclusion principle, the two electrons cannot

occupy these states.

The Schro¨dinger equation for these two electrons is

−

¯h

(∇

+ ∇

)ψ + V (r

, r

)ψ =(E +2E

)ψ, (5.7)

where E

is the Fermi energy, and V (r

, r

) is the potential energyof electron-

electron interaction. Substituting the wavefunction obtained in the center of

mass into the Schro¨dinger equation, we have the following equation for g(k):

¯h

g(k)+





g(k





=(E +2E

)g(k), (5.8)

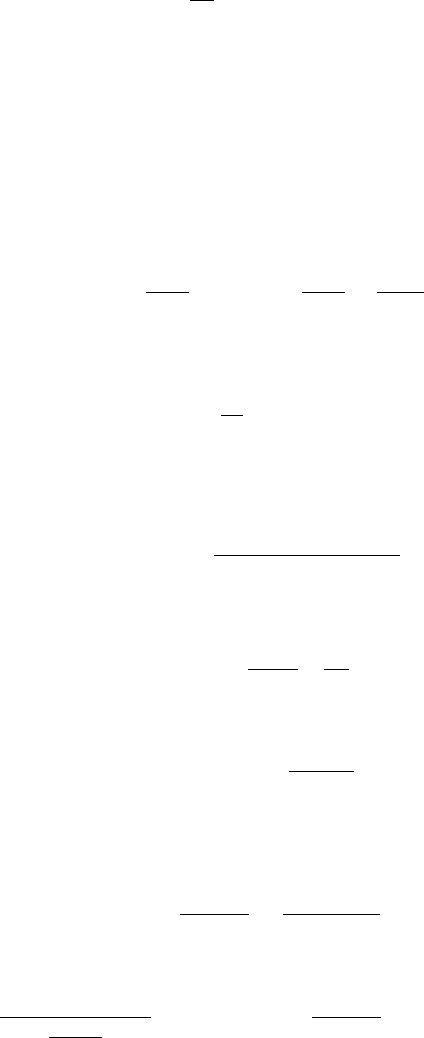
First group of superconductors: Mechanism of superconductivity 147

where





V (r)e

i(k−k



r, (5.9)

is a matrix element of the electron-electron interaction, and L

is the volume.

To solve this equation, it is necessary to know V



explicitly. Taking into

account that the energies of electrons participating in pairing is |ε

|, |ε



|≤

¯hω

, where ω

is the Debye frequency, we choose a simple form of the

electron-electron interaction





−V for |ε

|, |ε



|≤¯hω

0 otherwise,

(5.10)

where

¯h

− E

¯h

−

¯h

, (5.11)

and k

is the wave vector on the Fermi surface. In this case, Equation (5.8)

transforms into

g(k)



E +2E

−

¯h



= −V





g(k



)=C, (5.12)

where C is a constant independent of k. From Eq. (5.12), one can easily obtain

the following self-consistent equation

1=V



¯h

/m − E −2E

. (5.13)

If we introduce the density of states per spin direction

N(ε)=

4π

(2π)

dε

, (5.14)

we obtain

1=V

¯hω



N(ε)

2ε − E

dε. (5.15)

Since, in metals ¯hω

 E

∼ 5eVand¯hω

∼ 25 meV), then N(ε) 

N(0), and we can write

N(0) V

E −2¯hω

. (5.16)

The last equation can be re-written as

E = −

2¯hω



exp

N(0) V

− 1



−2¯hω

exp −

N(0) V

if N(0) V  1. (5.17)

148 ROOM-TEMPERATURE SUPERCONDUCTIVITY

The energy gain E (because E<0) indicates that the two electrons form a

bound state and, as a consequence, other electrons can also condense into this

state.

This result is obtained under the assumption that q =0[see Eq. (5.5)]. In

the case if q =0, the energy gain is E(q)=E(0)+¯hqv

. This means that

the energy gain is a maximum when q =0. The energy gain depends also on

the orientation of spin of each electron. The absolute value of E is a maximum

when the spins of the two electrons are oppositely directed (s

= −s

). Since

the distance between two electrons in a pair is sufﬁciently large,

¯hv

 10

− 10

◦

, (5.18)

and since the density of conduction electrons in metals is relatively high, the

wavefunctions of different pairs are largely overlap. To estimate the distance

between electrons in a pair, we used ¯hω

 300 K and N(0)V  0.3. The

sketch of electron-pair wavefunction is shown in Fig. 2.3, and their overlap in

Fig. 4.1.

3.2 Electron-electron attraction via phonons

How can electrons in a solid attract each other? The Coulomb force act-

ing between electrons is always repulsive, so that, the matrix element of the

Coulomb interaction, V

, is always positive, V

> 0. In order to obtain an at-

traction between electrons, it is necessary that they interact with a “third party,”

leading to the formation of electron pairs. In a solid, electrons constantly in-

teract with lattice vibrations.

Considering the interaction of two electrons via a virtual phonon, as shown

in Fig. 5.1, the element of the total matrix can in general be presented as

(k, k



, q)=k, k



|V |k − q, k



+ q =

k,k−q



k−q

− ε

− ¯hω

, (5.19)

where M

k,k−q

is the matrix element of the electron-phonon interaction, and

¯hω

is the energy of a phonon with the wave vector q shown in Fig. 5.1 [not be

confused with the vector q in Eq. (5.4)]. If we add to this process another one

in which the electron k



emits a phonon with the wave vector −q, we obtain

that the element of the total matrix becomes



2¯hω

k,k−q

(ε

k−q

− ε

)

− (¯hω

)

(5.20)

in which the element of the electron-phonon matrix M depends weakly on k.

The matrix element V



is negative if |ε

k−q

− ε

| < ¯hω

. In this case,

the electron-electron interaction is attractive. This interaction becomes repul-

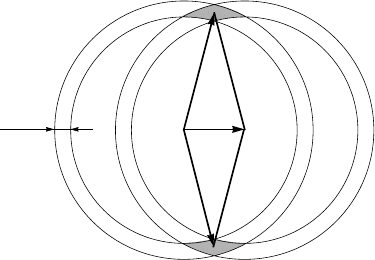
First group of superconductors: Mechanism of superconductivity 149

∆

O’

Figure 5.6. If electron pairs have a total momentum 2q, the interaction involves only the

electrons occupying k states within the dashed areas.

sive when the characteristic frequencies of electrons exceed the frequencies of

lattice vibrations. This will happen when heavy ions cannot follow the move-

ments of electrons. The interaction is a maximum when the two frequencies—

electronic and lattice vibrations—coincide. Taking into account the Coulomb

repulsion between the electrons, the total interaction (V

+ V

) will be at-

tractive (i.e. negative) if |V

| >V

The attraction is greatest for electrons with equal and opposite wave vectors

= −k

). Why? A transition of an electron pair from the state (k

, k

)

to the state (k



, k



), as shown in Fig. 5.1, must obey the low of momentum

conservation:

+ k

= k



+ k



. (5.21)

For example, if k

+ k

=2q as illustrated in Fig. 5.6, only the electrons

occupying the k states in the dashed areas of momentum space are allowed to

participate in the transitions. The dashed area is maximum when q = 0, and all

states within a band of width ∼ 2¯hω

near the Fermi surface are available.

3.3 Electron distribution in the ground state of a

superconductor

In this subsection, our objective is to investigate the state of a superconduc-

tor at T = 0, i.e. when its energy is a minimum.

As shown by Cooper, in the presence of an attractive interaction, the elec-

trons in a solid will condense at low temperature in pairs. In its turn, the BCS

theory supplies a formalism capable to treat the correlations of the pairs when

the number of interacting electrons is macroscopic.

150 ROOM-TEMPERATURE SUPERCONDUCTIVITY

In the framework of the BCS theory, it is ﬁrst assumed that the element V



of the matrix V = |V

|−V

(thus, V>0) has a simple form, namely,





−V for |ε

|, |ε



|≤¯hω

0 otherwise.

(5.22)

As was already discussed above, this means that only electrons with energies

that differ from the Fermi energy by no more than the Debye energy ¯hω

are

attracted to each other. This layer is schematically shown in Fig. 5.4.

The second postulate of the BCS theory is that the difference in energy

between the normal and the superconducting states originates exclusively from

the energy gain of electron pairing, and other forms of energy are not affected

by the superconducting transition. Each transition (k, −k) → (k



, −k



) is

accompanied by a contribution of −V to the condensation energy. Below T

the normal electrons are also present, but all become paired at T = 0. So,

the condensation energy is a maximum at T = 0. If the pair state (k, −k)

is occupied only by one electron, all the transitions (k



, −k



) → (k, −k) are

forbidden.

Let us introduce two new functions of k, namely, v

and f

. Suppose that

gives the probability that the pair state (k, −k) is occupied. Then, the prob-

ability for the pair state (k, −k) being empty is u

=1− v

. Suppose that

is the probability for the pair state (k, −k) is occupied by one (normal)

electron. Then, the probability for the electronic states k and −k both being

empty, i.e. being not occupied by single electrons simultaneously, is (1 - 2f

Finally, the probability for the pair state (k, −k) being occupied and the pair

state (k



, −k



) being empty is [v

(1 −v



)]

1/2

= v



. It is worth noting that,

in the pair wavefunction in Eq. (5.5), g(k) ≡ v

Let us now express the ﬁrst three terms in the Hemholtz free energy

F = E − TS = E

+ E

− TS + NE

(5.23)

through the probability functions v

, u

and f

, where N is total number of

electrons and E

is the Fermi energy. The kinetic energy is



[ε

+(1− 2f

], (5.24)

where ε

is the energy of an electron in the state k measured from the Fermi

level, given by Eq. (5.11).

The potential energy is

= V





(1 − 2f

)(1 − 2f



). (5.25)

TS = −2k



log f

+(1− f

) log(1 − f

)], (5.26)

First group of superconductors: Mechanism of superconductivity 151

we assume that the entropy comes exclusively from normal electrons which

are fermions.

In equilibrium, the free energy F has a minimum. Then, the equilibrium

values of v

and f

can be obtained by minimizing the free energy with respect

to v

and f

∂F

∂v

= 0 and

∂F

∂f

=0. (5.27)

Taking these derivations and introducing the quantity

∆

= V





(1 − 2f



) (5.28)

which has the dimensions of energy, one obtains the following equations

= ε

+∆

(5.29)

= −ε

+∆

where



+∆

. (5.30)

The solutions of these two equations are



1 −



(5.31)





. (5.32)

The minus sign in Eq. (5.31) stems from a general argument that, as k → 0,

we ought to have v

→ 1 while ε

→−E

. The dependence of v

on k is

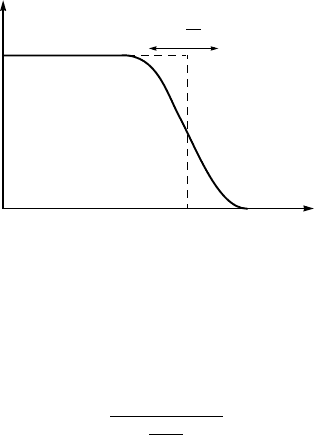
illustrated in Fig. 5.7. As one can see, for a normal metal at T = 0, v

has

a discontinuity at k

, while the total energy of a superconductor reaches its

minimum when the electron distribution in the vicinity of the Fermi level is

“smeared out” over the energy interval ∼ 2∆

. It is important to emphasize

that this occurs at absolute zero! Such a ground state of the superconductor is

a consequence of the interaction between electrons.

From Fig. 5.7, one can make a very important conclusion. At T = 0, the

kinetic energy of electrons near the Fermi level, forming the superconducting

condensate, is larger than that of a normal metal. Thus, the superconducting

condensation leading to a reduction in potential energy is accompanied by an

increase in kinetic energy. Nevertheless, this reduction in potential energy is

more than enough to compensate the Coulomb repulsion and the increase in

kinetic energy. The total energy of the superconducting condensate is thereby

reduced relative to that of the conventional one-electron description of states

in a metal. Thus, in the framework of the BCS theory, superconductivity in

conventional superconductors is driven by potential energy.

152 ROOM-TEMPERATURE SUPERCONDUCTIVITY

2∆

Figure 5.7. Dependence of v

on k at T = 0, or the probability of pair occupancy in the

superconducting ground state.

The second condition for equilibrium in Eq. (5.27) gives

exp

. (5.33)

At T = 0, f

= 0, meaning that all the electrons occupy the lowest energy

levels, and there are no excitations in the system.

3.4 Energy gap

In Eq. (5.30), E

presents a new spectrum of elementary excitations in a

superconductor, which is separated from the ground-state energy level by an

energy gap ∆

. The new spectrum of a superconductor is sketched in Fig.

5.8. At T = 0, the Cooper pairs occupy their ground-state level separated

by ∆

from the next energy level of elementary excitations. However, the

lowest amount of energy which can be absorbed by the superconductor is 2∆

and not ∆

. Why? Because if one electron becomes excited and jumps at

the ﬁrst energy level above the ground-state level, its ex-partner is still at the

ground-state level. Such a situation is forbidden, so the two electrons must be

excited simultaneously. As a consequence, the minimum energy needed for

this process is 2∆

. In other words, the energy 2∆

is necessary to break up a

Cooper pair.

It is worth to emphasize that, in a conventional superconductor, the Cooper

pairs cannot be excited. They are either at the ground-state energy level, or

they are already broken up. There is nothing in between. This, however, is

not the case for unconventional superconductors where the Cooper pairs can

be excited, being still paired.

Since the energy gap depends on temperature, ∆(T ), the minimum energy

needed for breaking up a Cooper pair varies with temperature as well. Let us

determine the ∆(T ) dependence. Substituting Eqs. (5.31), (5.32) and (5.33)

First group of superconductors: Mechanism of superconductivity 153

∆

ground

state

elementary

excitations

Figure 5.8. Elementary excitation spectrum of a superconductor at T = 0. The energy gap ∆

separates the ﬁrst excited level from the ground-state level.

into Eq. (5.28), the latter one reduces to

∆(T )=V



∆(T )



1 −

exp(E

T )+1



. (5.34)

The replacement of summation with integration yields, after simple algebra,

N(0)V

¯hω



dε



+∆

(T )

tanh



+∆

(T )

, (5.35)

where N (0) is the density of states of a superconductor at the Fermi level

at T =0(see the following subsection). This temperature dependence of

the energy gap, obtained in the framework of the BCS theory, is illustrated

in Fig. 2.12. As we shall see, near T

the gap varies with temperature as

∆(T ) ∝ (T

− T )

1/2

At T = 0, Equation (5.35) becomes

N(0)V

¯hω



dε



+∆

. (5.36)

Carrying out the integration, we have

∆

¯hω

sinh

N(0)V

 2¯hω

exp



−

N(0)V



if N(0)V  1. (5.37)

In reality, N(0)V ≤ 0.3. Let us estimate ∆

. Taking the Debye tempera-

ture Θ=¯hω

∼ 280 K and N (0)V = 0.3, one obtains ∆

∼ 10 K =

0.86 meV.