Morling K. Geometric and Engineering Drawing

Geometric and Engineering Drawing144

25 25

12.5

75 75

60° 45°

Dimensions in mm

P

Figure 10

30°

38 mm

X

Figure 11

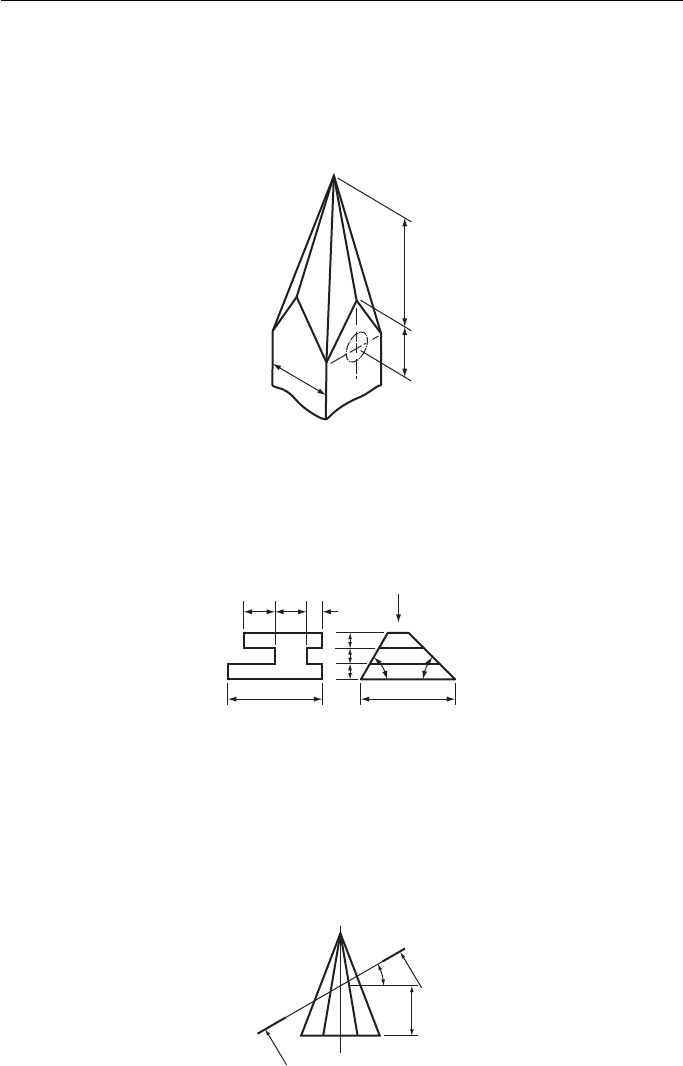
9. Figure 9 shows a church steeple which is square in plan, to a scale of 1:100 draw:

(a) a front elevation;

(b) a sectional plan on a cutting plane 2600 mm above the centre of the clock.

Ignore the chain lines.

South-East Regional Examinations Board

10. Draw the two elevations of the machined section shown in Fig. 10 and add a plan in the

direction of the arrow P showing hidden lines. Scale: full size.

Oxford and Cambridge Schools Examination Board

3600 mm

5300

mm

8000 mm

Figure 9

11. Figure 11 shows the elevation of a right hexagonal pyramid of base edges 35 mm and ver-

tical height 80 mm. Draw the given elevation and the true shape of the surface contained

in the section plane X – X.

University of London School Examinations

Orthographic Projection (First Angle and Third Angle) 145

30°

K

37

37 7612 37

74

Dimensions in mm

12 12

12

25 37

50

R18

R37

34

2550

Figure 12

12. Three views of a model of a steam turbine are shown in Fig. 12 .

Draw, to a scale of half-full size, showing all hidden detail:

(a) the given plan and FE;

(b) an AP in the direction of ‘ KK ’ .

Associated Examining Board

12

30°

R9

9

38

76

88

Dimensions in mm

FE

A

62

12

Figure 13

13. Details of an angle bracket are shown in Fig. 13 . Draw the two given views, the view

as seen from the direction of arrow A and an elevation as seen from the left of the FE  .

Hidden detail need not be shown. Scale: full size; use first angle orthographic projection.

Oxford Local Examinations

Geometric and Engineering Drawing146

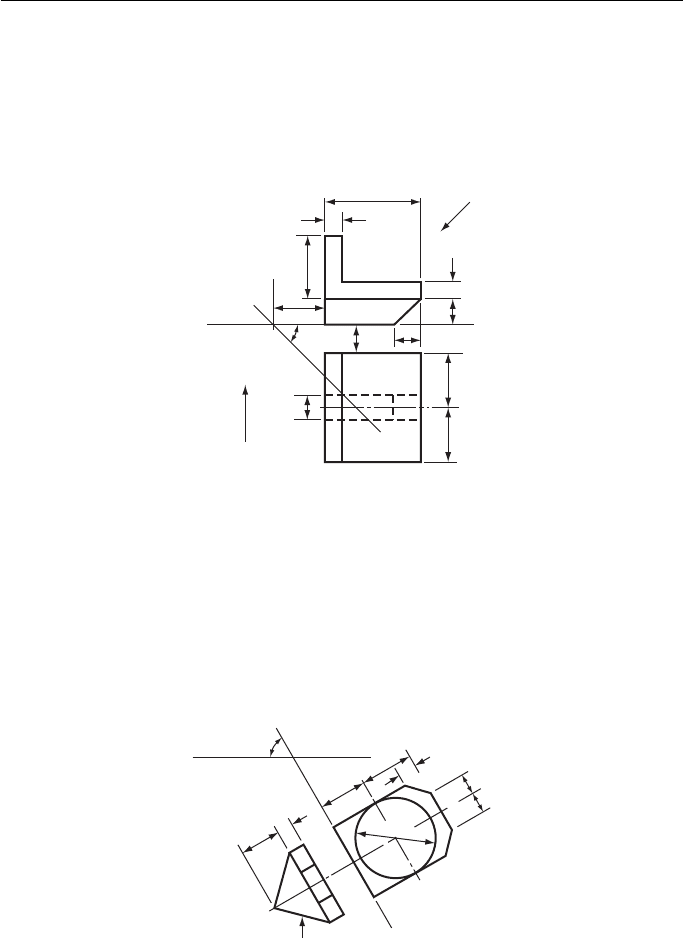
15. Two views of a pivot block are shown in Fig. 15 . Draw the given views, and produce an

elevation on XY as seen when looking in the direction of arrow A . Hidden edges are to be

shown.

Cambridge Local Examinations

60°

28

34

φ 56

37.5

12.5

X

1

Y

1

Y

A

Dimensions in mm

Figure 15

14. The plan and elevation of a special angle bracket are shown in Fig. 14 .

(a) Draw, full size, the given views and project an AP on the ground line X

1

– Y

1

.

(b) Using the AP in (a) above, project an AE on the ground line X

2

– Y

2

.

All hidden detail to be shown.

Associated Examining Board

64

10

18

3737

18

Dimensions in mm

45°

18

44

37

X

1

Y

1

X

2

Y

2

Figure 14

Orthographic Projection (First Angle and Third Angle) 147

3.75

4.5

51768

Dimensions in mm

X

φ 11.5

R2

3

45°

φ 6.25

φ 5

5

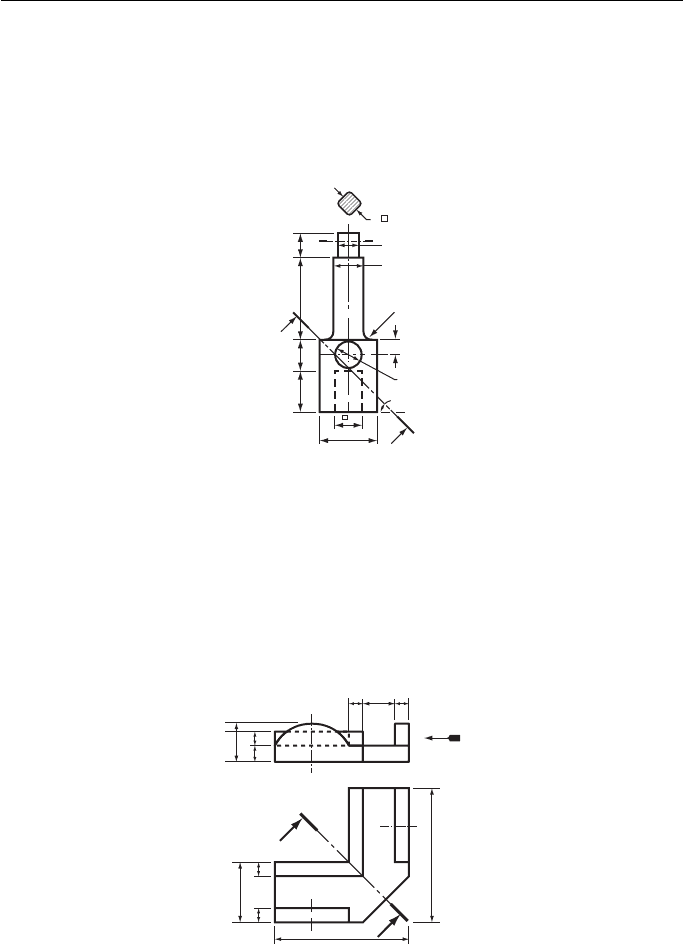
Figure 16

17. Figure 17 shows an elevation and a plan of a casting of a corner cramp in which the shape

is symmetrical about AA.

Draw a second elevation looking in the direction of arrow B .

Draw a sectional elevation on the cutting plane AA. Hidden detail is required on all views.

Southern Universities ’ Joint Board

1111

47

11

30

12.5

1111 25

B

A

Dimensions in mm

105

Figure 17

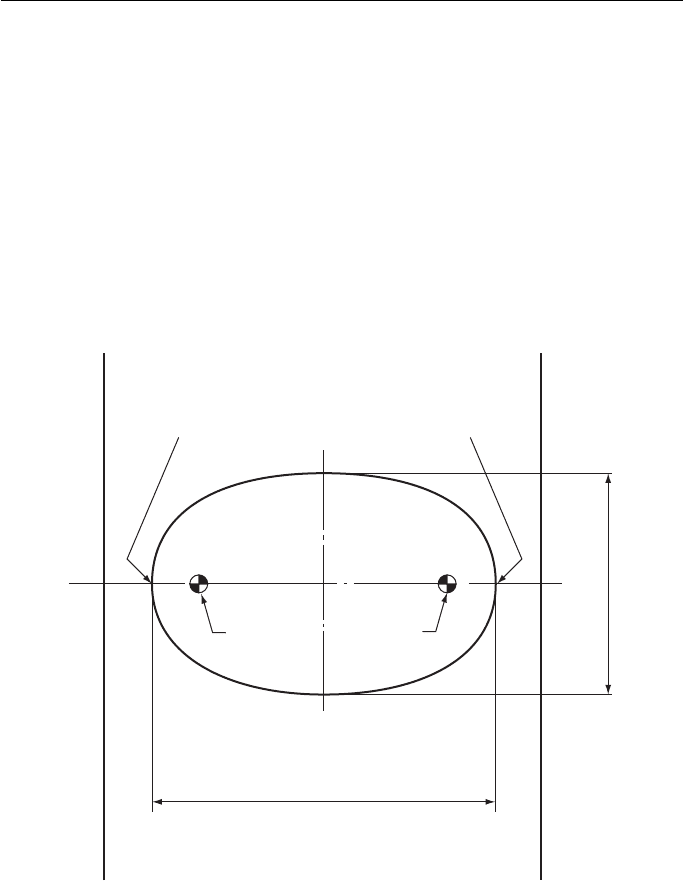
16. Figure 16 illustrates an elevation of an extension leg for a socket spanner.

Draw, to a scale of 4:1 and in first angle orthographic projection:

(a) the given elevation;

(b) a plan;

(c) the true shape of the section at the cutting plane XX.

Oxford Local Examinations

This page intentionally left blank

Geometric and Engineering Drawing. DOI:

10.1016/B978-0-08-096768-4.00011-5

Conic Sections – the Ellipse,

the Parabola, the Hyperbola

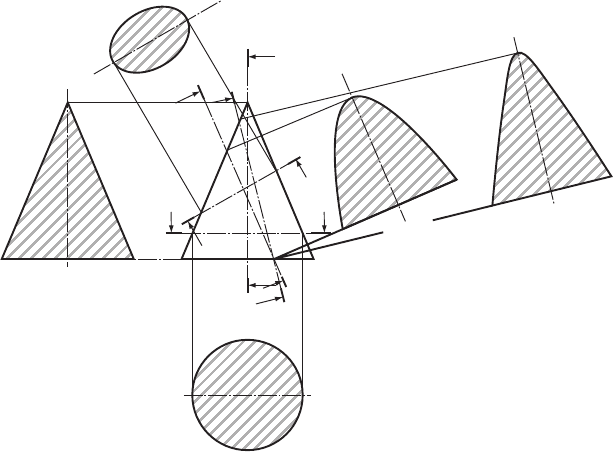
Figure 11.1 shows the five sections that can be obtained from a cone. The trian-

gle and the circle have been discussed in earlier chapters; this chapter looks at the

remaining three sections: the ellipse, the parabola and the hyperbola. These are three

very important curves. The ellipse can vary in shape from almost a circle to almost a

straight line and is often used in designs because of its pleasing shape. The parabola

can be seen in the shape of electric fire reflectors, radar dishes and the main cable of

suspension bridges. Both the parabola and the hyperbola are much used in civil engi-

neering. The immense strength of structures that are parabolic or hyperbolic in shape

has led to their use in structures made of pre-cast concrete and where large unsup-

ported ceilings are needed.

11

First angle projection

Hyperbola

section 5-5

(More acute than

side of cone)

Triangle

section 1-1

(Vertical - on c

L

)

Circle

section 2-2

(Horizontal)

1

4

5

3

2

Ellipse

section 3-3

(Less acute than side of cone)

Parabola

section 4-4

(Parallel to

side of cone)

Figure 11.1 Conic sections.

Geometric and Engineering Drawing150

The height of the cone and the base diameter, with the angle of the section rel-

ative to the side of the cone, are the factors that govern the relative shape of any

ellipses, parabolas or hyperbolas. There are an infinite number of these curves and,

given eternity and the inclination to do so, you could construct them all by taking

sections from cones. There are other ways of constructing these curves. This chapter,

as well as showing how to obtain them by plotting them from cones, shows some

other equally important methods of construction.

The Ellipse

Figure 11.2 shows an ellipse with the important features labelled.

Ver tex Ver tex

FocusFocus

Directrix

Minor axis

Major axis

Figure 11.2 The ellipse.

Conic Sections – the Ellipse, the Parabola, the Hyperbola 151

The ellipse as a conic section.

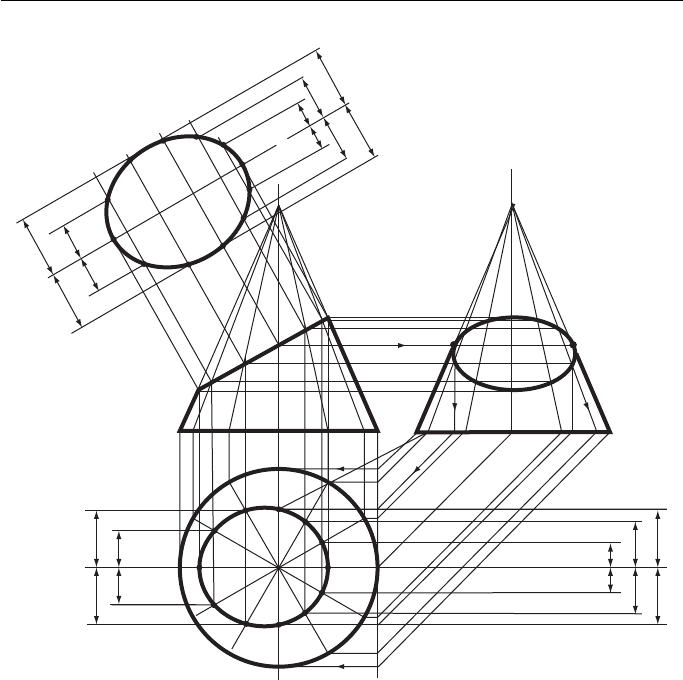
Figure 11.3 shows in detail how to project an ellipse as a section of a cone. The

shape across X – X is an ellipse.

First draw the FE, the EE and the plan of the complete cone. Divide the plan into

12 equal sectors with a 60 ° set square. Project these sectors onto the FE and the EE

where they appear as lines drawn on the surface of the cone from the base to the

apex. The points where these lines cross X – X can be easily projected across to the

EE and down to the plan to give the shape of X – X on these elevations. The point on

the centre line must be projected onto the plan via the EE (follow the arrows).

The shape of X – X on the plan is not the true shape since, in the plan, X – X is slop-

ing down into the page. However, the widths of the points, measured from the centre

line, are true lengths and can be transferred from the plan to the auxiliary view with

dividers to give the true shape across X – X. This is the ellipse.

First angle projection

c

d

e

a

b

a

d

c

e

b

a

X

Angle of X–X to base is less than the side of the cone

True shape across x–x

(Ellipse)

Figure 11.3

Geometric and Engineering Drawing152

The ellipse as a locus.

Definition

An ellipse is the locus of a point that moves so that its distance from a fixed point

(called the focus) bears a constant ratio, always less than 1, to its perpendicular distance

from a straight line (called the directrix). An ellipse has two foci and two directrices.

Directrix

DP

20

F (Focus)

Dimensions in mm

R10

R20

R30

R40

R50

4

3

× 10

Eccentricity

3

4

3

× 20

4

3

× 30

4

3

× 40

4

3

× 50

FP DP,=

3

4

FP (FP+20), Hence FP = 60=

3

4

Figure 11.4

Figure 11.4 shows how to draw an ellipse given the relative positions of the focus

and the directrix, and the eccentricity. In this case the focus and the directrix are

20 mm apart and the eccentricity is

3

4

.

The first point to plot is the one that lies between the focus and the directrix. This

is done by dividing DF in the same ratio as the eccentricity

, 4:3. The other end of the

ellipse, point P, is found by working out the simple algebraic sum shown on Fig. 11.4 .

The condition for the locus is that it is always

3

4

as far from the focus as it is from

the directrix. It is therefore

4

3

as far from the directrix as it is from the focus. Thus, if

the point is 30 mm from F, it is

40

3

mm

from the directrix; if the point is 20 mm from

F, it is

4

3

 20 mm from the directrix; if the point is 30 mm from F, it is

3

4

 3 0 m m

from the directrix. This is continued for as many points as may be necessary to draw

Conic Sections – the Ellipse, the Parabola, the Hyperbola 153

an accurate curve. The intersections of radii drawn from F and lines drawn parallel to

the directrix, their distance from the directrix being proportional to the radii, give the

outline of the ellipse. These points are joined together with a neat freehand curve.

To construct an ellipse by concentric circles.

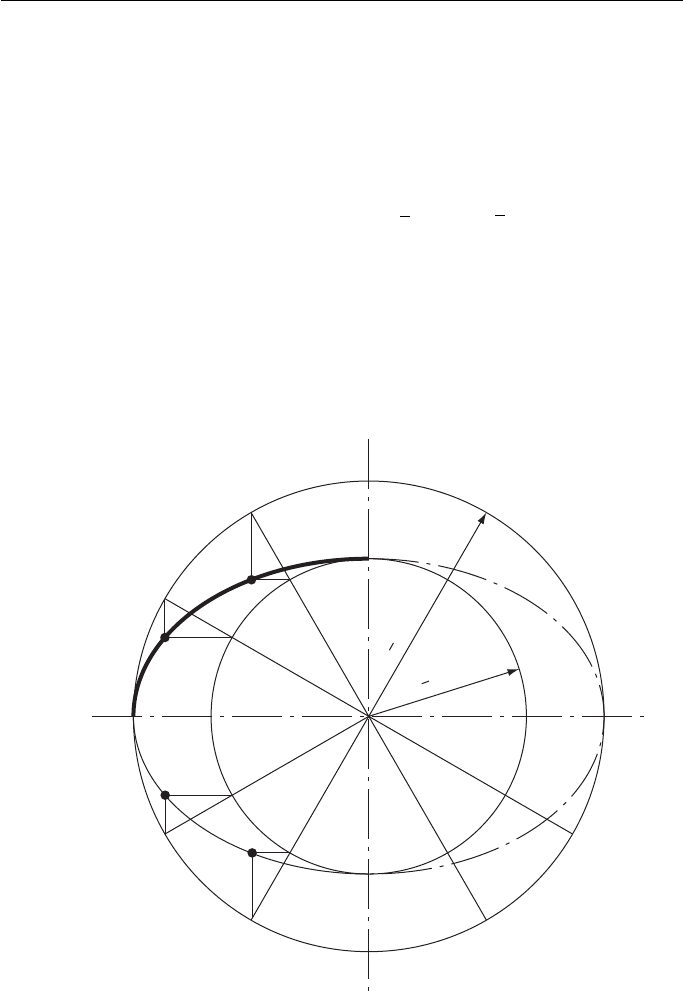
We now come to the first of three simple methods of constructing an ellipse. All

three methods need only two pieces of information for the construction – the lengths

of the major and minor axes.

Stage 1. Draw two concentric circles, radii equal to

1

2

major and

1

2

minor axes.

Stage 2. Divide the circle into a number of sectors. If the ellipse is not too large, 12 will

suffice as shown in Fig. 11.5 .

Stage 3. Where the sector lines cross the smaller circle, draw horizontal lines towards the

larger circle. Where the sector lines cross the larger circle, draw vertical lines to meet the

horizontal lines.

Stage 4. Draw a neat curve through the intersections.

Stage 4 Stage 1

Stage 2Stage 3

R = Major axis

1

2

R = Minor axis

1

2

Figure 11.5

Morling K. Geometric and Engineering Drawing

Подождите немного. Документ загружается.