Moran M.J., Shapiro H.N. Fundamentals of Engineering Thermodynamics
Подождите немного. Документ загружается.

Inserting values into the expression for the rate of heat transfer
Q
#
cv
5 W
#
cv
1 n
#
F
1
h
P
2 h
R
2
5 150 hp2
`
2545 Btu
/
h
1 hp
``
1 h
3600 s
`
1 c3.5 3 10
25
lbmol1fuel
2
s
d321,752,251 2 12107,53024
Bt
u
lbmol1fuel2
5222
.
22 B
tu
/
s
➊ These expressions correspond to Eqs. 13.12b and 13.15b, respectively.
Ability to…
❑
balance a chemical reaction
equation for complete com-
bustion of octane with
theoretical air.
❑
apply the control volume
energy balance to a reacting
system.
❑
evaluate enthalpy values
appropriately.
✓Skills Developed
If the density of octane is 5.88 lb/gal, how many gallons of fuel
would be used in 2 h of continuous operation of the engine? Ans. 4.9 gal.
13.2 Conservation of Energy—Reacting Systems 793
Analysis: The balanced chemical equation for complete combustion of methane with the theoretical amount of air is
given by Eq. 13.4
CH
4
1 2
1
O
2
1 3.76N
2
2
S
CO
2
1 2H
2
O 1 7.52N
2
Analyzing a Gas Turbine Fueled with Methane
c c c c EXAMPLE 13.5 c
Methane (CH
4
) at 258C, enters the combustor of a simple open gas turbine power plant and burns completely
with 400% of theoretical air entering the compressor at 258C, 1 atm. Products of combustion exit the turbine at
730 K, 1 atm. The rate of heat transfer from the power plant is estimated as 3% of the net power developed.
Determine the net power developed, in MW, if the fuel mass flow rate is 20 kg/min. For the entering air and
exiting combustion products, kinetic and potential energy effects are negligible.
SOLUTION
Known:
Steady-state operating data are provided for a simple gas turbine power plant.
Find: The net power developed, in MW, for a given fuel mass flow rate.
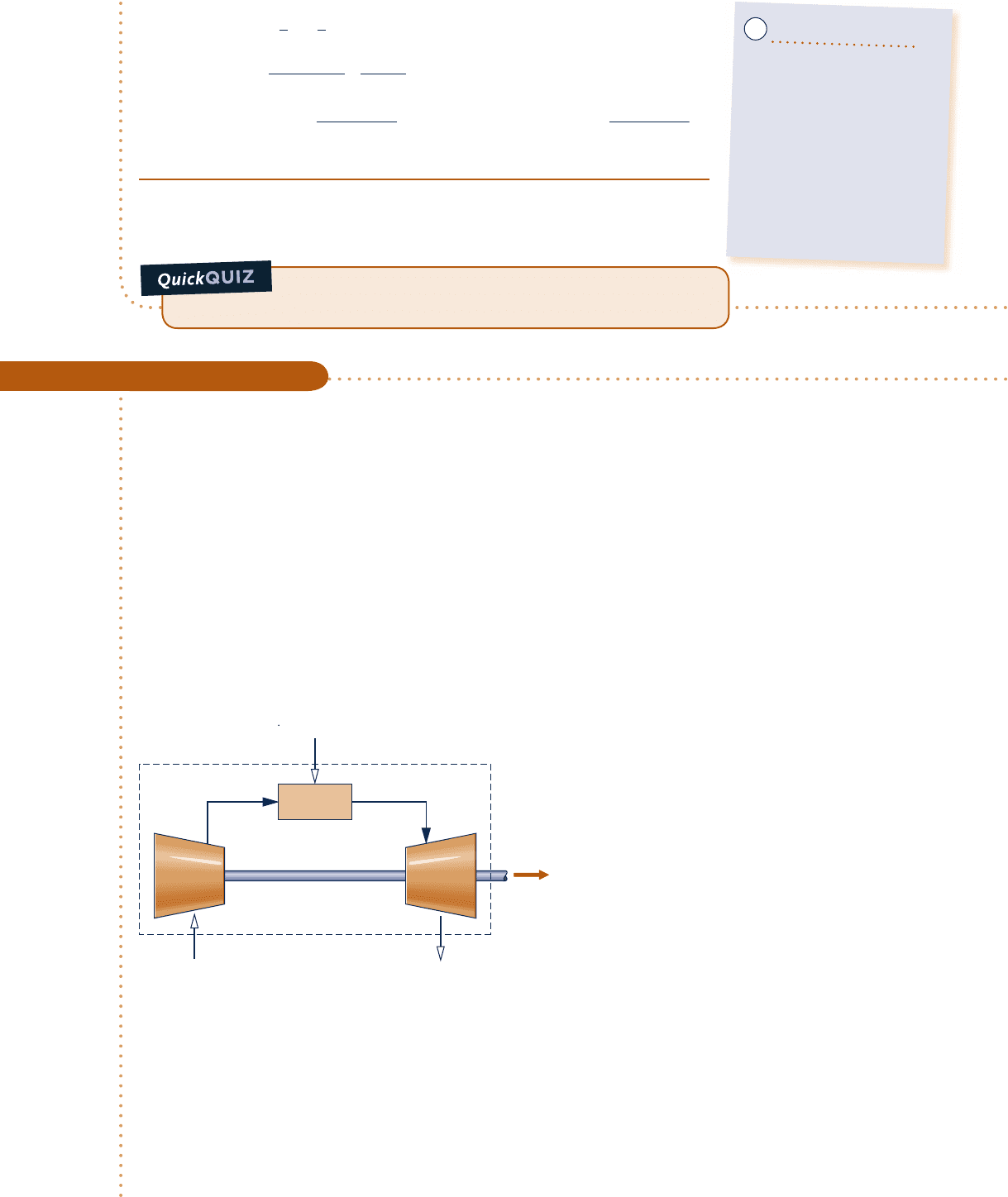
Schematic and Given Data:
Engineering Model:
1.
The control volume identified by a dashed
line on the accompanying figure operates
at steady state.
2. Kinetic and potential energy effects can
be ignored where mass enters and exits
the control volume.
3. The ideal gas model is applicable to the
fuel; the combustion air and the products
of combustion each form ideal gas mixtures.
4. Each mole of oxygen in the combustion air
is accompanied by 3.76 moles of nitrogen,
which is inert. Combustion is complete.
Fig. E13.5
Combustor
TurbineCompressor
W
cv
·
400% theoretical air
25°C, 1 atm
combustion products (CO
2
, H
2
O, O
2
, and N
2
)
730 K, 1 atm
CH
4
, 25°C
m
F
= 20 kg/min
c13ReactingMixturesandCombustion793 Page 793 7/13/10 11:00:46 AM user-s146c13ReactingMixturesandCombustion793 Page 793 7/13/10 11:00:46 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
794 Chapter 13
Reacting Mixtures and Combustion
For combustion of fuel with 400% theoretical air
CH
4
1
1
4.0
2
2
1
O
2
1 3.76N
2
2
S
aCO
2
1 bH
2
O 1 cO
2
1 d N
2
Applying conservation of mass to carbon, hydrogen, oxygen, and nitrogen, respectively
C:
1
5 a
H: 4 5 2
b
O:
1
4.0
21
2
21
2
2
5 2a 1 b 1 2c
N:
1
4.0
21
2
21
3.76
21
2
2
5 2d
Solving these equations, a 5 1, b 5 2, c 5 6, d 5 30.08.
The balanced chemical equation for complete combustion of the fuel with 400% of theoretical air is
CH
4
1 8
1
O
2
1 3.76N
2
2
S
CO
2
1 2H
2
O
1
g
2
1 6O
2
1 30.08N
2
The energy rate balance reduces, with assumptions 1–3, to give
➊
0 5
Q
#
cv
n
#
F
2
W
#
cv
n
#
F
1 h
R
2 h
P
Since the rate of heat transfer from the power plant is 3% of the net power developed, we have Q
#
cv
520.03W
#
cv
.
Accordingly, the energy rate balance becomes
1.03W
#
cv
n
#
F
5 h
R
2 h
P
Evaluating terms, we get
1.03W
#
cv
n
#
F
5 53h8
f
1 ¢h4
0
CH
4
1 83h8
f
0
1 ¢h4
O
2
0
1 30.083h8
f
0
1 ¢h4
0
N
2
6
2 53h8
f
1 ¢h4
CO
2
1 23h8
f
1 ¢h4
H
2
O1g2
1 63h8
f
0
1 ¢h4
O
2
1 30.083h8
f
0
1 ¢h4
N
2
6
where each coefficient is the same as the corresponding term of the balanced chemical equation and Eq. 13.9
has been used to evaluate enthalpy terms. The enthalpy of formation terms for oxygen and nitrogen are zero;
and ¢
h
5
0
for each of the reactants because the fuel and combustion air enter at 258C.
With the enthalpy of formation for CH
4
(g) from Table A-25
➋ h
R
5 1h8
f
2
CH
4
1g2
5274,850 kJ
/
kmol1fuel2
With enthalpy of formation values for CO
2
and H
2
O(g) from Table A-25, and enthalpy values for CO
2
, H
2
O, O
2
,
and N
2
at 730 K and 298 K from Table A-23
h
P
5
3
2393,520 1 28,622 2 9,364
4
1 2
3
2241,820 1 25,218 2 9,904
4
1 6
3
22,177 2 8,682
4
1 30.08
3
21,529 2 8,669
4
h
P
52359,475 kJ
/
kmol
1
fuel
2
Using the molecular weight of methane from Table A-1, the molar flow rate of the fuel is
n
#
F
5
m
#
F
M
F
5
20 kg
1
fuel
2
/
min
16.04 kg
1
fuel
2
/
kmol
1
fuel
2
`
1 min
60 s
`
5 0.02078 kmol1fuel2
/
s
Inserting values into the expression for the power
W
#
cv
5
n
#
F
1h
R
2 h
P
2
1.
03
W
#
cv
5
a
0.02078
kmol
1
fuel
2
s
b
3274,850 2 12359,47524
kJ
kmol1fuel2
1.
03
∞
1 MW
10
3
kJ
s
∞
5 5.74 MW
c13ReactingMixturesandCombustion794 Page 794 7/13/10 11:00:50 AM user-s146c13ReactingMixturesandCombustion794 Page 794 7/13/10 11:00:50 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Analyzing Closed Systems
Let us consider next a closed system involving a combustion process. In the absence
of kinetic and potential energy effects, the appropriate form of the energy balance is
U
P
2 U
R
5
Q
2
W
where U
R
denotes the internal energy of the reactants and U
P
denotes the internal
energy of the products.
If the reactants and products form ideal gas mixtures, the energy balance can be
expressed as
a
P
nu 2
a
R
nu 5 Q 2 W
(13.16)
where the coefficients n on the left side are the coefficients of the reaction equation
giving the moles of each reactant or product.
Since each component of the reactants and products behaves as an ideal gas, the
respective specific internal energies of Eq. 13.16 can be evaluated as u 5 h 2 RT, so
the equation becomes
Q 2 W 5
a
P
n1h 2 RT
P
22
a
R
n1h 2 RT
R
2
(13.17a)
where T
P
and T
R
denote the temperature of the products and reactants, respectively. With
expressions of the form of Eq. 13.13 for each of the reactants and products, Eq. 13.17a
can be written alternatively as
Q 2 W 5
a
P
n1h8
f
1 ¢h 2 RT
P
22
a
R
n1h8
f
1 ¢h 2 RT
R
2
5
a
P
n1h8
f
1 ¢h22
a
R
n1h8
f
1 ¢h22 RT
P
a
P
n 1 RT
R
a
R
n
(13.17b)
The enthalpy of formation terms are obtained from Table A-25 or Table A-25E. The
¢
h
terms are evaluated from Table A-23 or Table A-23E.
The foregoing concepts are illustrated in Example 13.6, where a gaseous mixture
burns in a closed, rigid container.
Determine the net power developed, in MW, if the rate of
heat transfer from the power plant is 10% of the net power developed.
Ans. 5.38 MW.
13.2 Conservation of Energy—Reacting Systems 795
The positive sign indicates power is from the control volume.
➊ This expression corresponds to Eq. 13.12b.
➋ In the combustor, fuel is injected into air at a pressure greater than 1 atm
because combustion air pressure has been increased in passing through the
compressor. Still, since ideal gas behavior is assumed for the fuel, the fuel
enthalpy is determined only by its temperature, 258C.
Ability to…
❑
balance a chemical reaction
equation for complete com-
bustion of methane with
400% of theoretical air.
❑
apply the control volume
energy balance to a reacting
system.
❑
evaluate enthalpy values
appropriately.
✓Skills Developed
c13ReactingMixturesandCombustion795 Page 795 8/11/10 8:41:47 AM user-s146c13ReactingMixturesandCombustion795 Page 795 8/11/10 8:41:47 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
796 Chapter 13
Reacting Mixtures and Combustion
c c c c EXAMPLE 13.6 c
A mixture of 1 kmol of gaseous methane and 2 kmol of oxygen initially at 258C and 1 atm burns completely in a
closed, rigid container. Heat transfer occurs until the products are cooled to 900 K. If the reactants and products
each form ideal gas mixtures, determine (a) the amount of heat transfer, in kJ, and (b) the final pressure, in atm.
SOLUTION
Known:
A mixture of gaseous methane and oxygen, initially at 258C and 1 atm, burns completely within a closed
rigid container. The products are cooled to 900 K.
Find: Determine the amount of heat transfer, in kJ, and the final pressure of the combustion products, in atm.
Schematic and Given Data:
Analyzing Combustion of Methane with Oxygen at Constant Volume
Analysis: The chemical reaction equation for the complete combustion of methane with oxygen is
CH
4
1 2O
2
S
CO
2
1 2H
2
O
1
g
2
(a) With assumptions 2 and 3, the closed system energy balance takes the form
U
P
2 U
R
5 Q 2 W
0
or
Q 5 U
P
2 U
R
5 11u
CO
2
1 2u
H
2
O1g2
22 11u
CH
4
1g2
1 2u
O
2
2
Each coefficient in this equation is the same as the corresponding term of the balanced chemical equation.
Since each reactant and product behaves as an ideal gas, the respective specific internal energies can be
evaluated as
u
5 h 2 RT. The energy balance then becomes
Q 5 311h
CO
2
2 RT
2
21 21h
H
2
O1g2
2 RT
2
242 311h
CH
4
1g2
2 RT
1
21 21h
O
2
2 RT
1
24
where T
1
and T
2
denote, respectively, the initial and final temperatures. Collecting like terms
Q 5 1h
CO
2
1 2h
H
2
O1g2
2 h
CH
4
1g2
2 2h
O
2
21 3R1T
1
2 T
2
2
The specific enthalpies are evaluated in terms of the respective enthalpies of formation to give
Q 5 31h8
f
1 ¢h2
CO
2
1 21h8
f
1 ¢h2
H
2
O1g2
2 1h8
f
1 ¢h
0
2
CH
4
1g2
2 21h8
f
0
1 ¢h2
O
2
0
41 3R1T
1
2 T
2
2
Since the methane and oxygen are initially at 2
5
8
C,
¢
h
5
0
for each of these reactants. Also, h8
f
5 0 for
oxygen.
Engineering Model:
1.
The contents of the closed, rigid
container are taken as the system.
2. Kinetic and potential energy effects
are absent, and W 5 0.
3. Combustion is complete.
4. The initial mixture and the products
of combustion each form ideal gas
mixtures.
5. The initial and final states are equilib-
rium states.
Fig. E13.6
1kmol CH
4
(g)
2 kmol O
2
T
1
p
1
= 25°C
= 1 atm
State 1
Products of
combustion
T
2
5 900 K
p
2
State 2
➊
c13ReactingMixturesandCombustion796 Page 796 8/12/10 7:34:30 AM user-s146c13ReactingMixturesandCombustion796 Page 796 8/12/10 7:34:30 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
With enthalpy of formation values for CO
2
, H
2
O(g) and CH
4
(g) from Table A-25 and enthalpy values for H
2
O
and CO
2
from Table A-23
Q 5
3
2393,520 1
1
37,405 2 9364
24
1 2
3
2241,820 1
1
31,828 2 9904
24
2
1
274,850
2
1 3
1
8.314
21
298 2 900
2
52745,436 kJ
(b) By assumption 4, the initial mixture and the products of combustion each form ideal gas mixtures. Thus, for
the reactants
p
1
V 5 n
R
RT
1
where n
R
is the total number of moles of reactants and p
1
is the initial pressure.
Similarly, for the products
p
2
V 5 n
P
RT
2
where n
P
is the total number of moles of products and p
2
is the final pressure.
Since n
R
5 n
P
5 3 and volume is constant, these equations combine to give
p
2
5
T
2
T
1
p
1
5 a
900 K
298 K
b 11 atm25 3.02 atm
➊ This expression corresponds to Eq. 13.17b.
Ability to…
❑
apply the closed system
energy balance to a reacting
system.
❑
evaluate property data
appropriately.
❑
apply the ideal gas equation
of state.
✓
Skills Developed
Calculate the volume of the system, in m
3
. Ans. 73.36 m
3
.
13.2.3
Enthalpy of Combustion and Heating Values
Although the enthalpy of formation concept underlies the formulations of the energy
balances for reactive systems presented thus far, the enthalpy of formation of fuels
is not always tabulated.
fuel oil and coal are normally composed of several individual
chemical substances, the relative amounts of which may vary considerably, depending
on the source. Owing to the wide variation in composition that these fuels can exhibit,
we do not find their enthalpies of formation listed in Tables A-25 or similar compila-
tions of thermophysical data. b b b b b
In many cases of practical interest, however, the enthalpy of combustion, which is
accessible experimentally, can be used to conduct an energy analysis when enthalpy
of formation data are lacking.
The enthalpy of combustion h
RP
is defined as the difference between the enthalpy
of the products and the enthalpy of the reactants when complete combustion occurs
at a given temperature and pressure. That is
h
RP
5
a
P
n
e
h
e
2
a
R
n
i
h
i
(13.18)
where the n’s correspond to the respective coefficients of the reaction equation giving
the moles of reactants and products per mole of fuel. When the enthalpy of combustion
is expressed on a unit mass of fuel basis, it is designated h
RP
. Tabulated values are usu-
ally given at the standard temperature T
ref
and pressure p
ref
introduced in Sec. 13.2.1.
The symbol h8
RP
or h8
RP
is used for data at this temperature and pressure.
The heating value of a fuel is a positive number equal to the magnitude of the
enthalpy of combustion. Two heating values are recognized by name: the higher heat-
ing value (HHV) and the lower heating value (LHV). The higher heating value is
obtained when all the water formed by combustion is a liquid; the lower heating value
enthalpy of combustion
higher and lower
heating values
13.2 Conservation of Energy—Reacting Systems 797
c13ReactingMixturesandCombustion797 Page 797 7/13/10 11:00:57 AM user-s146c13ReactingMixturesandCombustion797 Page 797 7/13/10 11:00:57 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

798 Chapter 13 Reacting Mixtures and Combustion
is obtained when all the water formed by combustion is a vapor. The higher heating
value exceeds the lower heating value by the energy that would be released were all
water in the products condensed to liquid. Values for the HHV and LHV also depend
on whether the fuel is a liquid or a gas. Heating value data for several hydrocarbons
are provided in Tables A-25.
The calculation of the enthalpy of combustion, and the associated heating value,
using table data is illustrated in the next example.
Calculating Enthalpy of Combustion of Methane
c c c c EXAMPLE 13.7 c
Calculate the enthalpy of combustion of gaseous methane, in kJ per kg of fuel, (a) at 25°C, 1 atm with liquid water
in the products, (b) at 25°C, 1 atm with water vapor in the products. (c) Repeat part (b) at 1000 K, 1 atm.
SOLUTION
Known:
The fuel is gaseous methane.
Find: Determine the enthalpy of combustion, in kJ per kg of fuel, (a) at 25°C, 1 atm with liquid water in the
products, (b) at 25°C, 1 atm with water vapor in the products, (c) at 1000 K, 1 atm with water vapor in the
products.
Engineering Model:
1.
Each mole of oxygen in the combustion air is accompanied by 3.76 moles of nitrogen, which is inert.
2. Combustion is complete, and both reactants and products are at the same temperature and pressure.
3. The ideal gas model applies for methane, the combustion air, and the gaseous products of combustion.
Analysis: The combustion equation is obtained from Eq. 13.4
CH
4
1 2O
2
1 7.52N
2
S
CO
2
1 2H
2
O 1 7.52N
2
Using Eq. 13.9 in Eq. 13.18, the enthalpy of combustion is
h
RP
5
a
P
n
e
1h8
f
1 ¢h2
e
2
a
R
n
i
1h8
f
1 ¢h2
i
Introducing the coefficients of the combustion equation and evaluating the specific enthalpies in terms of the
respective enthalpies of formation
h
RP
5 h
CO
2
1 2h
H
2
O
2 h
CH
4
1g2
2 2h
O
2
5 1h8
f
1 ¢h2
CO
2
1 21h8
f
1 ¢h2
H
2
O
2 1h8
f
1 ¢h2
CH
4
1g2
2 21h8
f
0
1¢h2
O
2
For nitrogen, the enthalpy terms of the reactants and products cancel. Also, the enthalpy of formation of oxygen
is zero by definition. On rearrangement, the enthalpy of combustion expression becomes
h
RP
5 1h8
f
2
CO
2
1 21h8
f
2
H
2
O
2 1h8
f
2
CH
4
1g2
1 31¢
h
2
CO
2
1 21¢h2
H
2
O
2 1¢h2
CH
4
1g2
2 21¢h2
O
2
4
5 h8
RP
1 31¢h2
CO
2
1 21¢h2
H
2
O
2 1¢h2
CH
4
1g2
2 21¢h2
O
2
4 (1)
The values for h8
RP
and 1¢h2
H
2
O
depend on whether the water in the products is a liquid or a vapor.
(a) Since the reactants and products are at 25°C, 1 atm in this case, the ¢h terms drop out of Eq. (1) giving the
expression for h
RP
. Thus, for liquid water in the products, the enthalpy of combustion is
h8
RP
5 1h 8
f
2
CO
2
1 21h8
f
2
H
2
O1l2
2 1h8
f
2
CH
4
1g2
With enthalpy of formation values from Table A-25
h8
RP
52393,520 1 212285,83022 1274,850252890,330 kJ
/
kmol1fuel2
c13ReactingMixturesandCombustio798 Page 798 8/11/10 10:40:43 AM user-s146 c13ReactingMixturesandCombustio798 Page 798 8/11/10 10:40:43 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

➊
➋
Dividing by the molecular weight of methane places this result on a unit mass of fuel basis
h8
RP
5
2890,330 kJ
/
kmol 1fuel2
16.04 kg 1fuel2
/
kmol 1fuel2
5255,507 kJ
/
kg 1fuel2
The magnitude of this value agrees with the higher heating value of methane given in Table A-25.
(b) As in part (a), the ¢h terms drop out of the expression for h
RP
, Eq. (1), which for water vapor in the products
reduces to h8
RP
, where
h8
RP
5 1h8
f
2
CO
2
1 21h8
f
2
H
2
O1g2
2 1h8
f
2
CH
4
1g2
With enthalpy of formation values from Table A-25
h8
RP
52393,520 1 212241,82022 1274,850252802,310 kJ
/
kmol 1fuel2
On a unit of mass of fuel basis, the enthalpy of combustion for this case is
h8
RP
5
2802,310
16.04
5250,019 kJ
/
kg 1fuel2
The magnitude of this value agrees with the lower heating value of methane given in Table A-25.
(c) For the case where the reactants and products are at 1000 K, 1 atm, the term h8
RP
in Eq. (1) giving the expres-
sion for h
RP
has the value determined in part (b): h8
RP
52802,310 kJ
/
kmol (fuel), and the ¢h terms for O
2
, H
2
O(g),
and CO
2
can be evaluated using specific enthalpies at 298 and 1000 K from Table A-23. The results are
1¢h2
O
2
5 31,389 2 8682 5 22,707 kJ
/
kmol
1¢h2
H
2
O1g2
5 35,882 2 9904 5 25,978 kJ
/
kmol
1¢h2
CO
2
5 42,769 2 9364 5 33,405 kJ
/
kmol
For methane, the c
p
expression of Table A-21 can be used to obtain
1¢h2
CH
4
1g2
5
#
1000
298
c
p
dT
5 R a3.826T 2
3.979
10
3
T
2
2
1
24.558
10
6
T
3
3
2
22.733
10
9
T
4
4
1
6.963
10
12
T
5
5
b
1000
298
5 38,189 kJ
/
kmol 1fuel2
Substituting values into the expression for the enthalpy of combustion, Eq. (1), we get
h
RP
52802,310 1 333,405 1 2125,97822 38,189 2 2122,70724
52800,522 kJ
/
kmol 1fuel2
On a unit mass basis
h
RP
5
2800,55
2
1
6.0
4
5249,910 kJ
/
kg 1fuel2
➊ Using Interactive Thermodynamics: IT, we get 38,180 kJ/kmol (fuel).
➋ Comparing the values of parts (b) and (c), the enthalpy of combustion of
methane is seen to vary little with temperature. The same is true for many
hydrocarbon fuels. This fact is sometimes used to simplify combustion
calculations.
Ability to…
❑
calculate the enthalpy of
combustion at standard
temperature and pressure.
❑
calculate the enthalpy of
combustion at an elevated
temperature and standard
pressure.
✓
Skills Developed
What is the lower heating value of methane, in kJ/kg (fuel)
at 25°C, 1 atm?
Ans. 50,020 kJ/kg (Table A-25).
13.2 Conservation of Energy—Reacting Systems 799
c13ReactingMixturesandCombustio799 Page 799 7/14/10 10:27:20 AM user-s146 c13ReactingMixturesandCombustio799 Page 799 7/14/10 10:27:20 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

800 Chapter 13
Reacting Mixtures and Combustion
adiabatic flame temperature
Evaluating Enthalpy of Combustion by Calorimetry
When enthalpy of formation data are available for all the reactants and products, the
enthalpy of combustion can be calculated directly from Eq. 13.18, as illustrated in
Example 13.7. Otherwise, it must be obtained experimentally using devices known as
calorimeters. Both constant-volume (bomb calorimeters) and flow-through devices are
employed for this purpose. Consider as an illustration a reactor operating at steady
state in which the fuel is burned completely with air. For the products to be returned
to the same temperature as the reactants, a heat transfer from the reactor would be
required. From an energy rate balance, the required heat transfer is
Q
cv
#
n
F
#
5
a
P
n
e
h
e
2
a
R
n
i
h
i
(13.19)
where the symbols have the same significance as in previous discussions. The heat
transfer per mole of fuel, Q
#
cv
y
n
#
F
, would be determined from measured data. Compar-
ing Eq. 13.19 with the defining equation, Eq. 13.18, we have h
RP
5 Q
#
cv
y
n
#
F
. In accord
with the usual sign convention for heat transfer, the enthalpy of combustion would
be negative.
As noted previously, the enthalpy of combustion can be used for energy analyses
of reacting systems.
consider a control volume at steady state in which a fuel oil reacts
completely with air. The energy rate balance is given by Eq. 13.15b
Q
#
cv
n
#
F
2
W
#
cv
n
#
F
5
a
P
n
e
1h8
f
1 ¢h2
e
2
a
R
n
i
1h8
f
1 ¢h2
i
All symbols have the same significance as in previous discussions. This equation can
be rearranged to read
Q
#
cv
n
#
F
2
W
#
cv
n
#
F
5
a
P
n
e
1h8
f
2
e
2
a
R
n
i
1h8
f
2
i
1
a
P
n
e
1¢h2
e
2
a
R
n
i
1¢h2
i
For a complete reaction, the underlined term is just the enthalpy of combustion h
8
RP
,
at T
ref
and
p
ref
. Thus, the equation becomes
Q
#
cv
n
F
#
2
W
#
cv
n
#
F
5 h
8
RP
1
a
P
n
e
1¢h2
e
2
a
R
n
i
1¢h2
i
(13.20)
The right side of Eq. 13.20 can be evaluated with an experimentally determined
value for h
8
RP
and ¢h values for the reactants and products determined as discussed
previously. b b b b b
13.3 Determining the Adiabatic
Flame Temperature
Let us reconsider the reactor at steady state pictured in Fig. 13.2. In the absence of
work W
#
cv
and appreciable kinetic and potential energy effects, the energy liberated
on combustion is transferred from the reactor in two ways only: by energy accompa-
nying the exiting combustion products and by heat transfer to the surroundings. The
smaller the heat transfer, the greater the energy carried out with the combustion
products and thus the greater the temperature of the products. The temperature that
would be achieved by the products in the limit of adiabatic operation of the reactor
is called the adiabatic flame temperature or adiabatic combustion temperature.
The adiabatic flame temperature can be determined by use of the conservation of
mass and conservation of energy principles. To illustrate the procedure, let us suppose
that the combustion air and the combustion products each form ideal gas mixtures.
c13ReactingMixturesandCombustio800 Page 800 7/14/10 10:27:25 AM user-s146 c13ReactingMixturesandCombustio800 Page 800 7/14/10 10:27:25 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New

Then, with the other assumptions stated previously, the energy rate balance on a per
mole of fuel basis, Eq. 13.12b, reduces to the form h
P
5 h
R
—that is
a
P
n
e
h
e
5
a
R
n
i
h
i
(13.21a)
where i denotes the incoming fuel and air streams and e the exiting combustion
products. With this expression, the adiabatic flame temperature can be determined
using table data or computer software, as follows.
13.3.1
Using Table Data
When using Eq. 13.9 with table data to evaluate enthalpy terms, Eq. 13.21a takes the form
a
P
n
e
1h
8
f
1 ¢h2
e
5
a
R
n
i
1h8
f
1 ¢h2
i
or
a
P
n
e
1¢h2
e
5
a
R
n
i
1¢h2
i
1
a
R
n
i
h8
fi
2
a
P
n
e
h8
fe
(13.21b)
The n’s are obtained on a per mole of fuel basis from the balanced chemical reaction
equation. The enthalpies of formation of the reactants and products are obtained
from Table A-25 or A-25E. Enthalpy of combustion data might be employed in situ-
ations where the enthalpy of formation for the fuel is not available. Knowing the
states of the reactants as they enter the reactor, the
¢h
terms for the reactants can
be evaluated as discussed previously. Thus, all terms on the right side of Eq. 13.21b
can be evaluated. The terms (¢
h
)
e
on the left side account for the changes in enthalpy
of the products from T
ref
to the unknown adiabatic flame temperature. Since the
unknown temperature appears in each term of the sum on the left side of the equa-
tion, determination of the adiabatic flame temperature requires iteration: A tempera-
ture for the products is assumed and used to evaluate the left side of Eq. 13.21b. The
value obtained is compared with the previously determined value for the right side
of the equation. The procedure continues until satisfactory agreement is attained.
Example 13.8 gives an illustration.
13.3.2
Using Computer Software
Thus far we have emphasized the use of Eq. 13.9 together with table data when
evaluating the specific enthalpies required by energy balances for reacting systems.
Such enthalpy values also can be retrieved using Interactive Thermodynamics: IT.
With IT, the quantities on the right side of Eq. 13.9 are evaluated by software, and
h
data are returned directly.
consider CO
2
at 500 K modeled as an ideal gas. The specific
enthalpy is obtained from IT as follows:
T = 500 // K
h = h_T(“CO
2
”, T)
Choosing K for the temperature unit and moles for the amount under the Units
menu, IT returns h 5 23.852 3 10
5
kJ/kmol.
This value agrees with the value calculated from Eq. 13.9 using enthalpy data for
CO
2
from Table A-23, as follows
h 5 h
8
f
1 3h1500 K22 h1298 K24
52393,520 1 317,678 2 93644
523.852 3 10
5
kJ
/
kmol b b b b b
TAKE NOTE...
The adiabatic flame tem-
perature can be determined
iteratively using table data
or IT. See Example 13.8.
13.3 Determining the Adiabatic Flame Temperature 801
c13ReactingMixturesandCombustio801 Page 801 7/13/10 11:41:06 AM user-s146 c13ReactingMixturesandCombustio801 Page 801 7/13/10 11:41:06 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
802 Chapter 13 Reacting Mixtures and Combustion
As suggested by this discussion, IT is also useful for analyzing reacting systems. In
particular, the equation solver and property retrieval features of IT allow the adia-
batic flame temperature to be determined without the iteration required when using
table data.
In Example 13.8, we show how the adiabatic flame temperature can be determined
iteratively using table data or Interactive Thermodynamics: IT.
Determining the Adiabatic Flame Temperature for Complete
Combustion of Liquid Octane
c c c c EXAMPLE 13.8 c
Liquid octane at 25°C, 1 atm enters a well-insulated reactor and reacts with air entering at the same temperature
and pressure. For steady-state operation and negligible effects of kinetic and potential energy, determine the
temperature of the combustion products for complete combustion with (a) the theoretical amount of air, (b) 400%
theoretical air.
SOLUTION
Known:
Liquid octane and air, each at 25°C and 1 atm, burn completely within a well-insulated reactor operating
at steady state.
Find: Determine the temperature of the combustion products for (a) the theoretical amount of air and (b) 400%
theoretical air.
Schematic and Given Data:
Engineering Model:
1.
The control volume indicated on the
accompanying figure by a dashed line
operates at steady state.
2. For the control volume, Q
#
cv
5 0,
W
#
cv
5 0, and kinetic and potential
effects are negligible.
3. The combustion air and the products of
combustion each form ideal gas mixtures.
4. Combustion is complete.
5. Each mole of oxygen in the combus-
tion air is accompanied by 3.76 moles
of nitrogen, which is inert.
Fig. E13.8
Air
25°C, 1 atm
Combustion products,
T
P
C
8
H
18
(l)
25°C, 1 atm
Insulation
Analysis: At steady state, the control volume energy rate balance Eq. 13.12b reduces with assumptions 2 and 3
to give Eq. 13.21a
a
P
n
e
h
e
5
a
R
n
i
h
i
(1)
When Eq. 13.9 and table data are used to evaluate the enthalpy terms, Eq. (1) is written as
a
P
n
e
1h8
f
1 ¢h2
e
5
a
R
n
i
1h
8
f
1¢h2
i
On rearrangement, this becomes
a
P
n
e
1¢h2
e
5
a
R
n
i
1¢h2
i
1
a
R
n
i
h8
fi
2
a
P
n
e
h8
fe
c13ReactingMixturesandCombustio802 Page 802 8/12/10 7:36:59 AM user-s146 c13ReactingMixturesandCombustio802 Page 802 8/12/10 7:36:59 AM user-s146 /Users/user-s146/Desktop/Merry_X-Mas/New/Users/user-s146/Desktop/Merry_X-Mas/New
