Мирошник И.В., Бобцов А.А. Теория автоматического управления
Подождите немного. Документ загружается.


Дифференцирующее звено (идеальное). Звено описывается дифференциальным уравнением
(2.63)
или, в операторной форме,
(2.64) .
Переходная функция дифференцирующего звена -
(2.65) ,
а реакция звена на линейно-нарастающий сигнал x
2
=t -
(2.66) .
При x
2
= const для любых t>0 выполняется и, следовательно, статической характеристикой звена
является прямая .
Рис. 2.12. Реакция дифференцирующего звена на линейно нарастающее воздействие
Примеры: тахогенератор (электромашинный датчик скорости), электронный дифференциатор (
).

Замечание 2.4. Выходом дифференцирующего звена является производная входного сигнала, т.е. его
мгновенная скорость dx
2
/dt. Операция нахождения текущего значения скорости x
1
(t)=dx
2
(t)/dt только по
информации об известном в данный момент времени t сигнале x
2
(t) физически не реализуема и поэтому идеальных
дифференцирующих звеньев не существует. Тем не менее производная может быть приближенно рассчитана как
1
(t)=D x
2
(t)/D t, где D t - интервал времени, D x
2
- соответствующее приращение сигнала x
2
. При уменьшении
интервала D t можно получить значение
1
(t), сколь угодно близкое к текущему значению скорости x
1
(t).
Следовательно, несмотря на нереализуемость (с абсолютной точностью) операции дифференцирования,
теоретически возможно построение звена, которое обеспечивает нахождение производной dx
2
(t)/dt со сколь
угодно высокой точностью.
Реальное дифференцирующее звено. Звено описывается уравнением
(2.67) .
или, в операторной форме,
(2.68)
Переходная функция звена имеет вид
Рис. 2.13. Переходная функция реального дифференцирующего звена
(2.69) ,
а реакция звена на линейно-нарастающий сигнал x
1
=t совпадает с переходной функцией апериодического
звена, т.е.
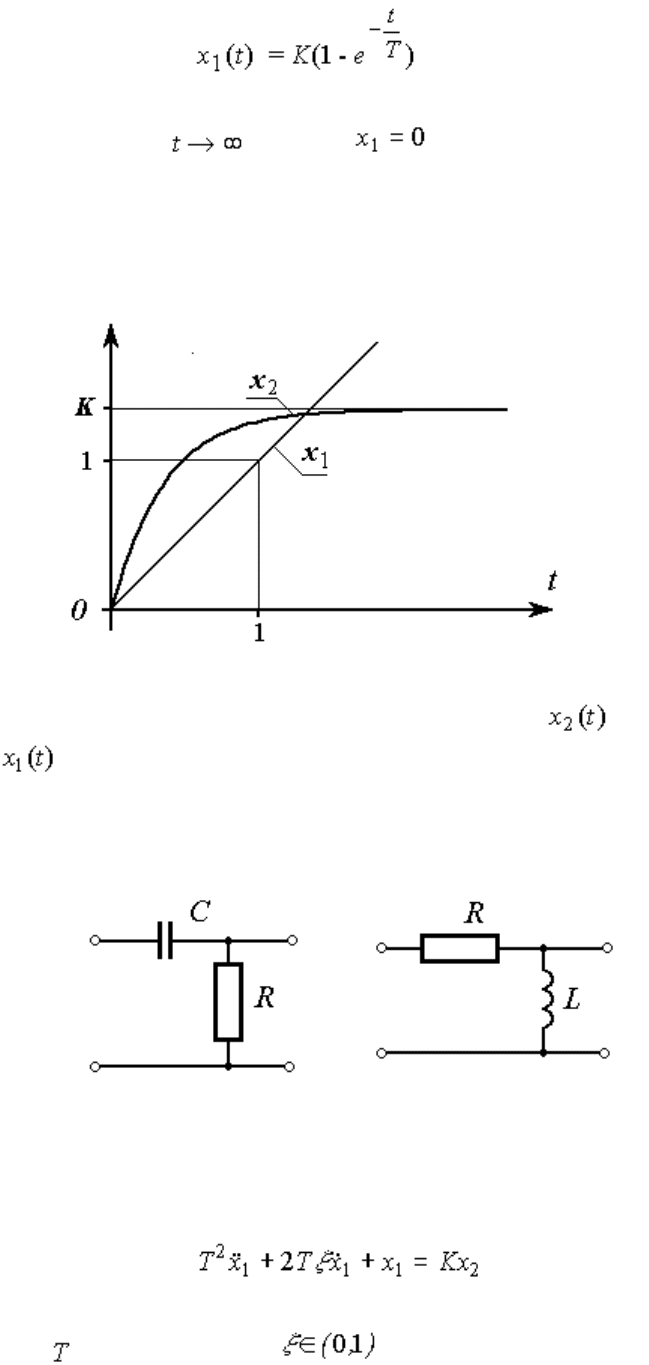
(2.70) .
При x
2
=const и выполняется , что соответствует статической характеристике звена.
При достаточно малых постоянных времени T, характеристики звена приближаются к характеристикам
идеального дифференцирующего звена (см. Замечание 2.4).
Рис. 2.14. Реакция реального дифференцирующего звена на линейно нарастающее воздействие
Примеры: CR и RL цепи.
Колебательное звено. Звено описывается дифференциальным уравнением 2-го порядка
(2.71) ,
- постоянная времени, - параметр затухания, или операторным уравнением (2.50), где
передаточная функция имеет вид

(2.72) .
Корни характеристического уравнения принимают значения
,
где - коэффициент затухания, - угловая частота
колебаний.
Переходная функция звена имеет вид
(2.73) ,
где ; , а статическая характеристика -
Рис. 2.15. Переходная функция колебательного звена
(2.74) .
Примеры: маятник в вязкой среде, - цепь.
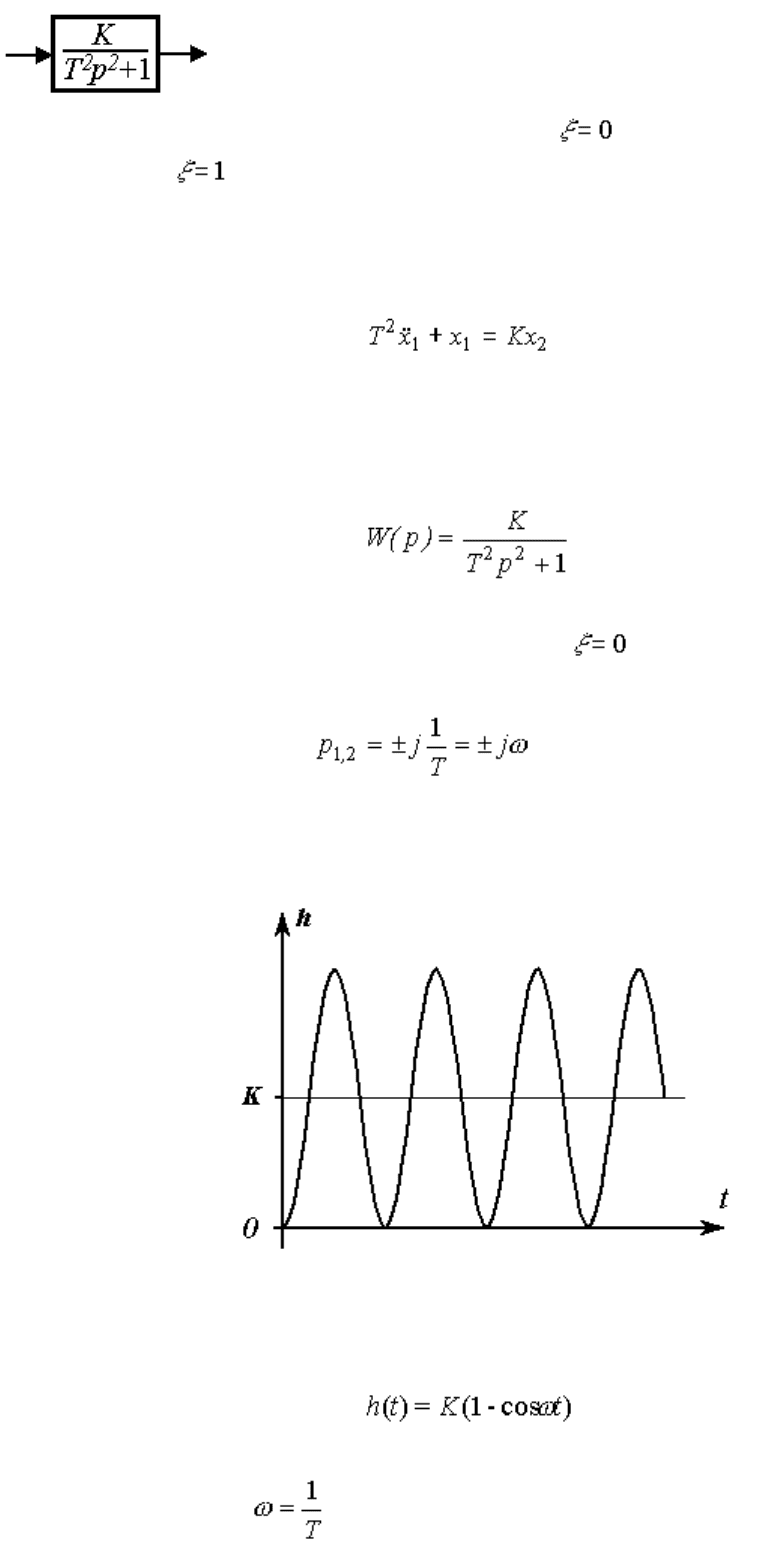
Замечание 2.5. В предельном случае при на выходе звена возникают незатухающие колебания, а при
- монотонный (апериодический) процесс, что соответствует рассматриваемым далее консервативному и
двойному апериодическому звену.
Консервативное звено (осциллятор). Звено описывается дифференциальным уравнением
(2.75)
или операторным уравнением (2.50), где
(2.76) ,
и получается из колебательного звена при . Консервативное звено имеет чисто мнимые полюсы
и переходную функцию вида
Рис. 2.16. Переходная функция колебательного звена
(2.77) ,
где . Звено не имеет статической характеристики.
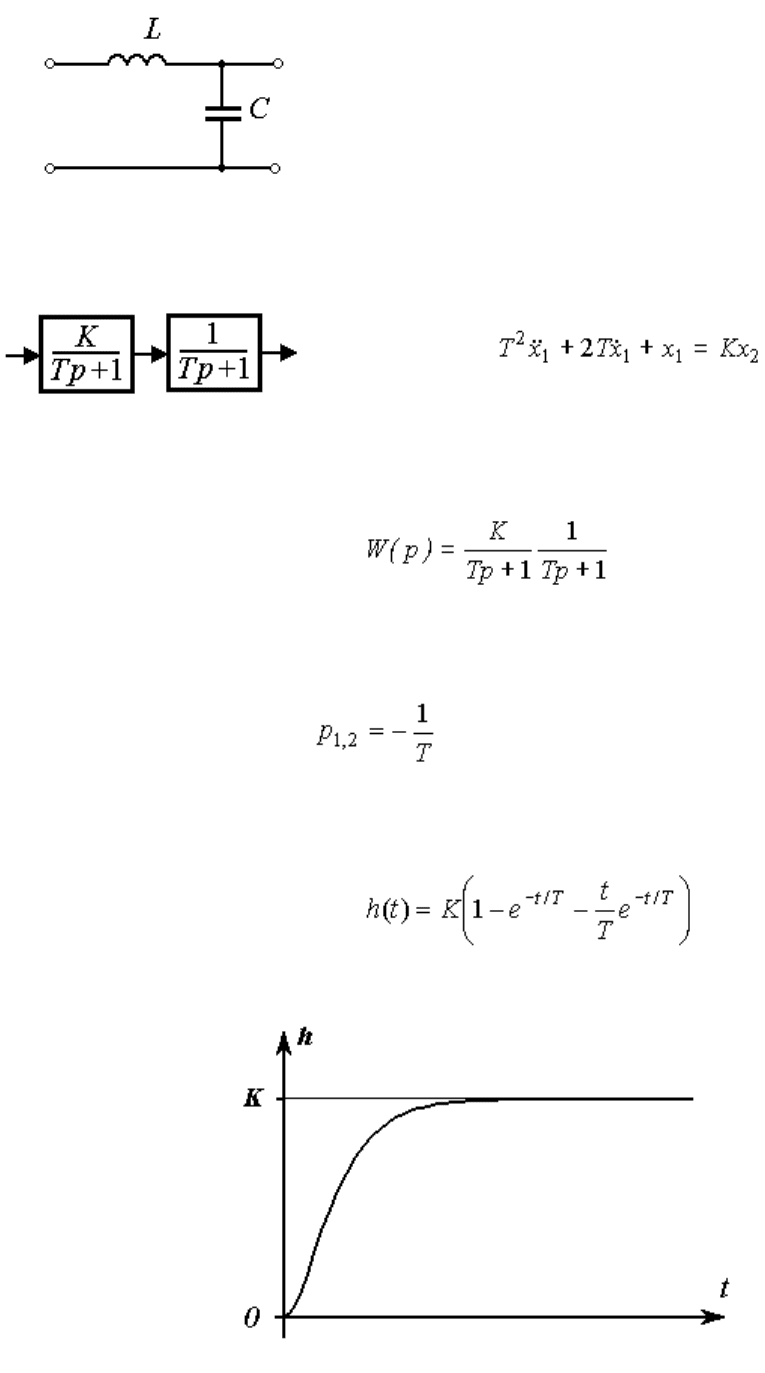
Примеры: маятник в вакууме; идеальный колебательный (LC) контур.
Двойное апериодическое звено. Звено описывается уравнением
(2.78)
или операторным уравнением (2.50), где
(2.79) .
Звено имеет равные вещественные корни характеристического уравнения
,
и переходную функцию
(2.80) .
Рис. 2.17. Переходная функция двойного апериодического звена
Статическая характеристика звена

(2.81) .
Уровень:
Принципы управления, модели регуляторов и
замкнутых систем
Напомним, что система управления состоит из двух основных блоков, (см. введение и рис. 4.7): объекта
управления (представленного управляемым процессом, измерительными и исполнительными устройствами, см.
например п. 4.1) и устройством управления, которое выполняет вычислительные функции, т.е. по определенным
правилам (алгоритмам) осуществляет обработку текущей информации об объекте и определяет управляющее
воздействие u(t). Алгоритмы работы этого устройства зависят от динамических свойств ОУ и конкретных задач,
решаемых системой. Работа системы управления происходит во взаимодействии с внешней средой, которая
оказывает возмущающее влияние на движение ОУ (сигнал f (t )), а также может выступать в роли внешнего
задающего блока (см. п. 4.2).
Рис. 4.7. Структура системы автоматического управления
Системы управления локального уровня обеспечивают решение задач стабилизации, слежения,
терминального управления и т.д. (см. п. 1.4.1), что предусматривает поддержание заданных законов изменения
регулируемых переменных y(t ) или переменных состояния x
i
(t ). Управление, обеспечивающее решение локальных
задач, осуществляется с помощью регулятора и задающего блока. Регулятор производит расчет управляющих
сигналов САУ на основании анализа текущих значений выходных переменных y(t ) и/или переменных состояния x
i
(t
), а также соответствующих задающих воздействий y*(t ) и/или x
i
*(t ), поступающих от внешней среды или
генерируемых задающим блоком (см. п. 4.2).
4.3.1. Принципы управления. С помощью регуляторов в систему управления вводятся контуры прямых и
обратных связей. В зависимости от структуры связей имеет место классификация принципов управления,
приведенная на рис. 4.8.
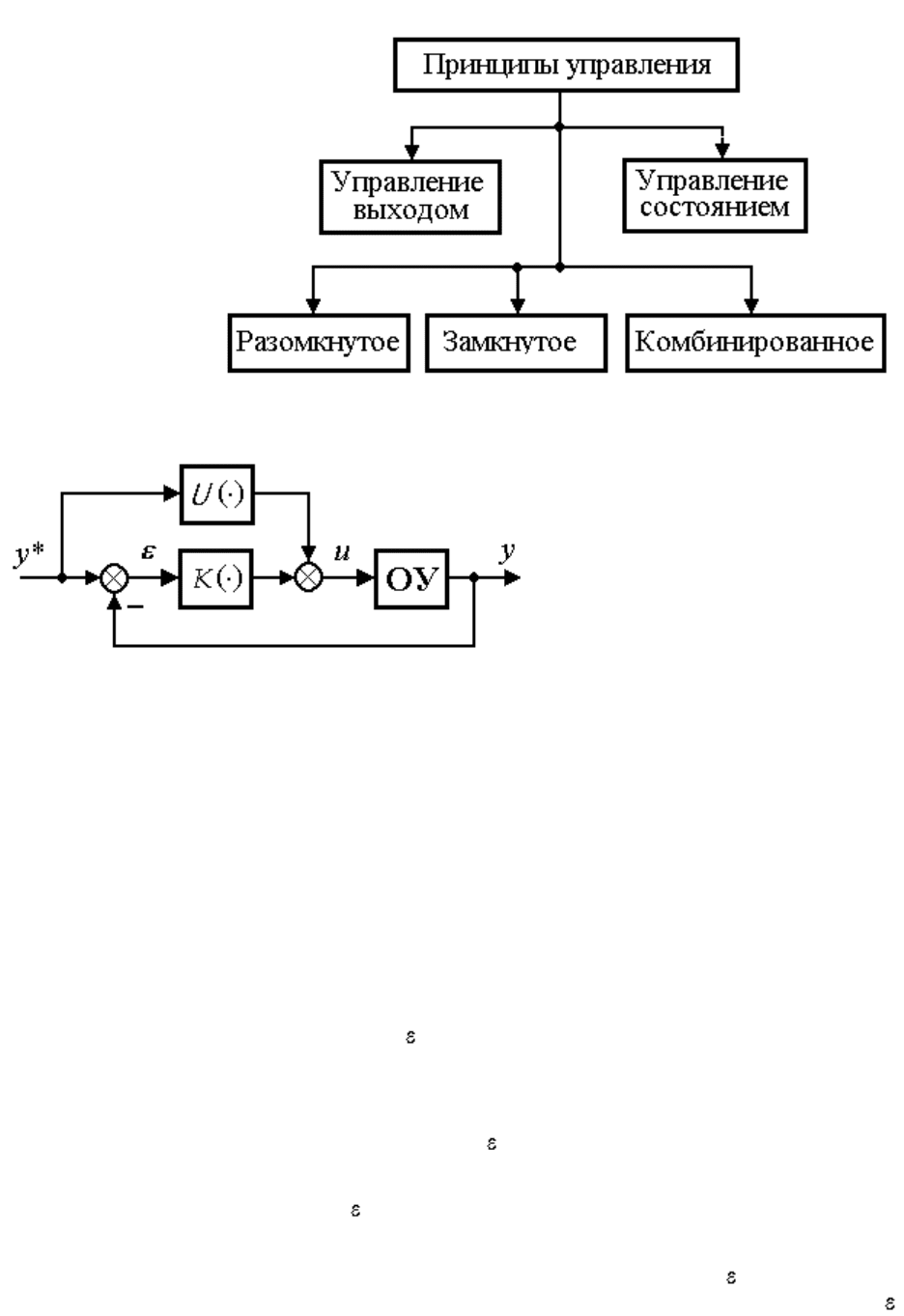
Рис. 4.8. Принципы управления
Попытка непосредственного решения локальных задач
приводит к управлению по выходу ОУ и простейшей
(классической) структуре САУ, содержащей контуры прямых
связей по задающему воздействию у* и обратных связей по
выходу у. При этом различают разомкнутое, замкнутое и
комбинированное управления. Последнии два типа
предусматривают наличие обратных связей по отклонению.
Разомкнутое управление вводит в состав системы контур прямой связи по задающему воздействию:
(4.68) u= U ( y*),
где U(·) - функциональный оператор. Управляющее воздействие рассчитывается из условия получения
заданного закона изменения выхода (задающего воздействия y*(t)), а текущее поведение ОУ не контролируется.
Отличие свойств реального объекта от его математической модели, используемой при построении алгоритма
(4.68), возможная неустойчивость ОУ и влияние возмущений , обычно приводят к неидентичности выхода y(t ) и
задающего воздействия y*(t), т.е. ошибкам разомкнутых систем управления ( см. п. 2.3.2 ).
Управление по отклонению вводит в структуру системы контур обратных связей:
(4.69) u = K ( ),
где рассогласование (отклонение) рассчитывается по формуле:
(4.70) = y*- y,
а оператор K (·) выбирается из условия уменьшения отклонения (t) в процессе работы системы. Так как в
данном случае поведение ОУ корректируется в зависимости от текущего значения , то управление по
отклонению обеспечивает устойчивость системы и уменьшение влияния возмущений (см. п. 2.3.2 ).
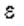
Абсолютная точность решения задачи управления может быть достигнута с помощью комбинированного
управления, предусматривающего использование как прямых, так и обратных связей :
(4.71) u = U(y*)+K( ).
В ряде случаев структура системы дополняется также контурами управления по возмущающему
воздействию f, что обеспечивает компенсацию возмущающего влияния внешней среды.
Системы управления одноканальными объектами, построенные по классическим принципам управления по
выходной переменной, содержат не более одного контура обратной связи и поэтому условно относятся к
одноконтурным системам .
Подключение дополнительных контуров обратной связи в многоконтурных системах обеспечивает
повышение качества управления. Наиболее полная информация об управляемом процессе содержится в
переменных состояния (см. п. 3.1.1), и поэтому управление по состоянию позволяет достичь наилучших
качественных показателей системы управления.
При управлении по состоянию, также как и управлении по выходу, различают разомкнутые алгоритмы вида
(4.72) u= U ( x*),
представляющие контуры прямых связей по задающему воздействию x*(t), замкнутые алгоритмы управления
(контуры обратных связей по отклонению):
(4.73) u = K (e),
где вектор рассогласований (отклонений ) e рассчитывается по формуле:
(4.74) e = x*- x,
и алгоритмы комбинированного типа :
(4.75) u = U (x*)+ K (e).
Основным функциональным элементом устройства управления является регулятор. В соответствии с
рассмотренными принципами управления (см. рис. 4.8) различают регуляторы выхода и состояния, разомкнутые
регуляторы и регуляторы комбинированного типа. В зависимости от функциональных операторов U ( )и K ( ),
встречающихся в алгоритмах (4.68) - (4.71) или (4.72) - (4.75), различают:
л инейные и нелинейные регуляторы ;
регуляторы с постоянными и переменными параметрами.
Дальнейшее изложение касается только линейных регуляторов и, соответственно , линейных замкнутых
систем управления.
Для описания отдельных блоков системы используются дифференциальные и операторные уравнения.
Модели системы в целом находятся как объединение блоков с использованием известных правил преобразования
(в том числе методов преобразования передаточных функций, см. п. 2.4.1) и могут быть получены в
операторном виде, соответствующем описанию вход-выход;
в виде скалярных или векторно-матричных дифференциальных уравнений - моделей вход-состояние-
выход.
4.3.2. Регуляторы выхода и модели одноконтурных систем. Одноконтурная система - простейший и
самый распространенный тип систем, обеспечиващих управление выходной переменной одноканального ОУ. В
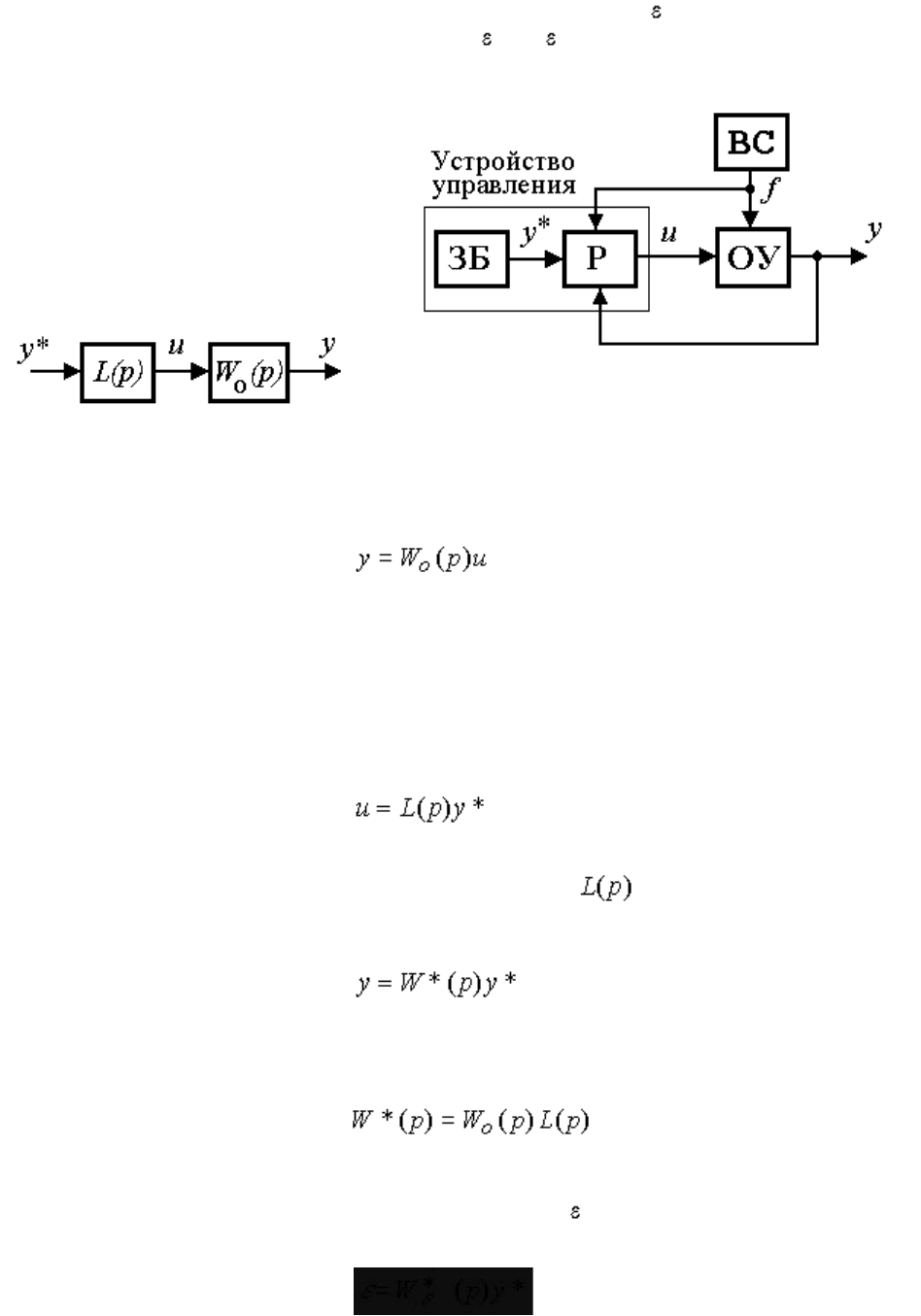
состав устройства управления одноконтурной САУ входит задающий блок ЗБ и регулятор выхода Р (рис. 4.9).
Задача системы заключается в минимизации отклонения = у* - у, чему препятствует возмущение f(t ) и
ненулевые начальные рассогласования (0) =
0
. Задача решается с помощью регуляторов выхода.
Рис.4.9. Одноконтурная система
Рассмотрим свойства систем управления линейным объектом, описываемым операторным уравнением
(4.76) ,
где W
О
(p) - передаточная функция ОУ, с различными типами регуляторов выхода.
Регуляторы разомкнутого типа представлены контуром прямой связи по задающему воздействию, т.е.
алгоритмом
(4.77) ,
где р =d/dt - оператор дифференцирования, - интегро-дифференциальный оператор (передаточная
функция регулятора). После подстановки (4.76) в (4.77) получаем уравнение вида
(4.78) ,
где W*(p) - передаточная функция разомкнутой системы
(4.79) .
Введем в рассмотрение ошибку слежения (4.70) и подставив (4.70) в (4.78), получим уравнение,
связывающее задающее воздействие y* и ошибку " (модель ошибки):
(4.80) .
Интегро-дифференциальный оператор
