Мирошник И.В., Бобцов А.А. Теория автоматического управления

Подождите немного. Документ загружается.

          ,

          .

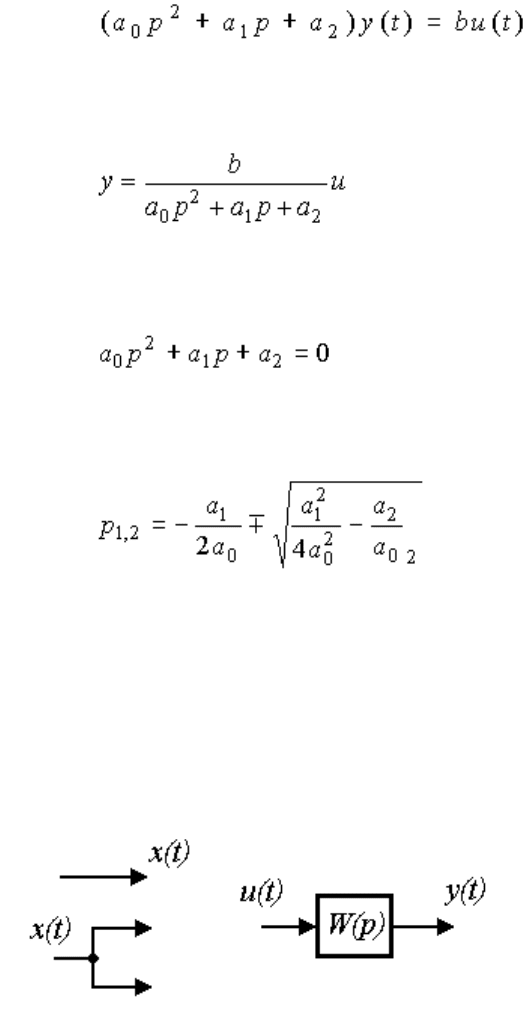
Характеристическое уравнение системы

         

имеет два (вещественных или комплексных) корня

          .



2.1.2. Структурные схемы. Наиболее распространенной графоаналитической формой модели

динамической системы является структурная схема - разновидность направленного графа. Элементами такой

схемы являются (рис. 2.1)



Рис. 2.1. Элементы структурной схемы

 буквенные обозначения сигналов (x(t), u(t), y(t) и т. д.) и т.д.;

 буквенные обозначения операторов (например, W(p));

 графические обозначения - стрелки, указывающие направление действия сигналов, узлы (разветвления

сигналов), блоки c указанием входных и выходных сигналов, а также операторов, описывающих связи

между сигналами.

К простейшим блокам, использующихся в структурных схемах, относятся (рис. 2.2):

 блок сравнения;

 сумматор;

 пропорциональный блок;

 интегратор

(см. также п. 2.3).

Рис.2.2. Простейшие блоки

Пример 2.2. Модели вход-выход нагревательной печи, RC- цепочки и разгона электродвигателя (см. пример

1 .1) описываются дифференциальным уравнением первого порядка

(2.9)          

где T, K - постоянные коэффициенты (параметры). Операторная форма модели имеет вид

(2.10)           .

Здесь - характеристическое уравнение, которое имеет один корень (полюс

системы) p

=-1/T . Из уравнения (2.10) находим операторную связь входа и выхода

         

Следовательно, передаточной функцией блока является оператор

          .

Заметим, что уравнение (2.9) можно привести к виду

(2.11)          

где a=1/T, b=K/T . Тогда операторная форма (2.10) принимает вид

(2.12)          

а форма (2.12) -

          .

Пример 2.3. Рассмотрим движение материальной точки массы m под действием силы (входного

воздействия) u=F(t) . Данная динамическая система описывается уравнением второго порядка (2-ым законом

Ньютона)

(2.13)          

с начальными условиями y

(0), , где y(t) - линейное перемещение. Операторная форма

модели принимает вид

(2.14)          

а характеристическое уравнение системы

(2.15)          

имеет два корня (полюса системы) p

1,2

=0 . Из уравнения (2.14) находим операторную связь

входа и выхода

(2.16)          

где b=1/m. Следовательно, передаточной функцией блока является оператор

(2.17)           .

В структурных схемах многомерных и многоканальных систем векторные сигналы ,

и иногда выделяют двойными стрелками.

2.1.3. Многоканальные модели. Сначала рассмотрим многоканальную систему с независимыми

(автономными) каналами. Система описывается m операторными уравнениями

[M2m]          

каждое из которых характеризует поведение одного из ее каналов.

Введем в рассмотрение векторы выходных переменных y и управления u:

          , ,

соответственно, и запишем систему уравнений в векторно-матричной форме:

         

или,

[М2m]           A(p)y=B(p)u

Если матрица A(p) - обратима, т.е. существует обратная матрица

          ,

то из уравнения [М2m] найдем

[М3m]           y=W(p)u,

где W(p)= {W

} - передаточная матрица системы (матричный интегро-дифференциальный оператор),

вычисляемая как

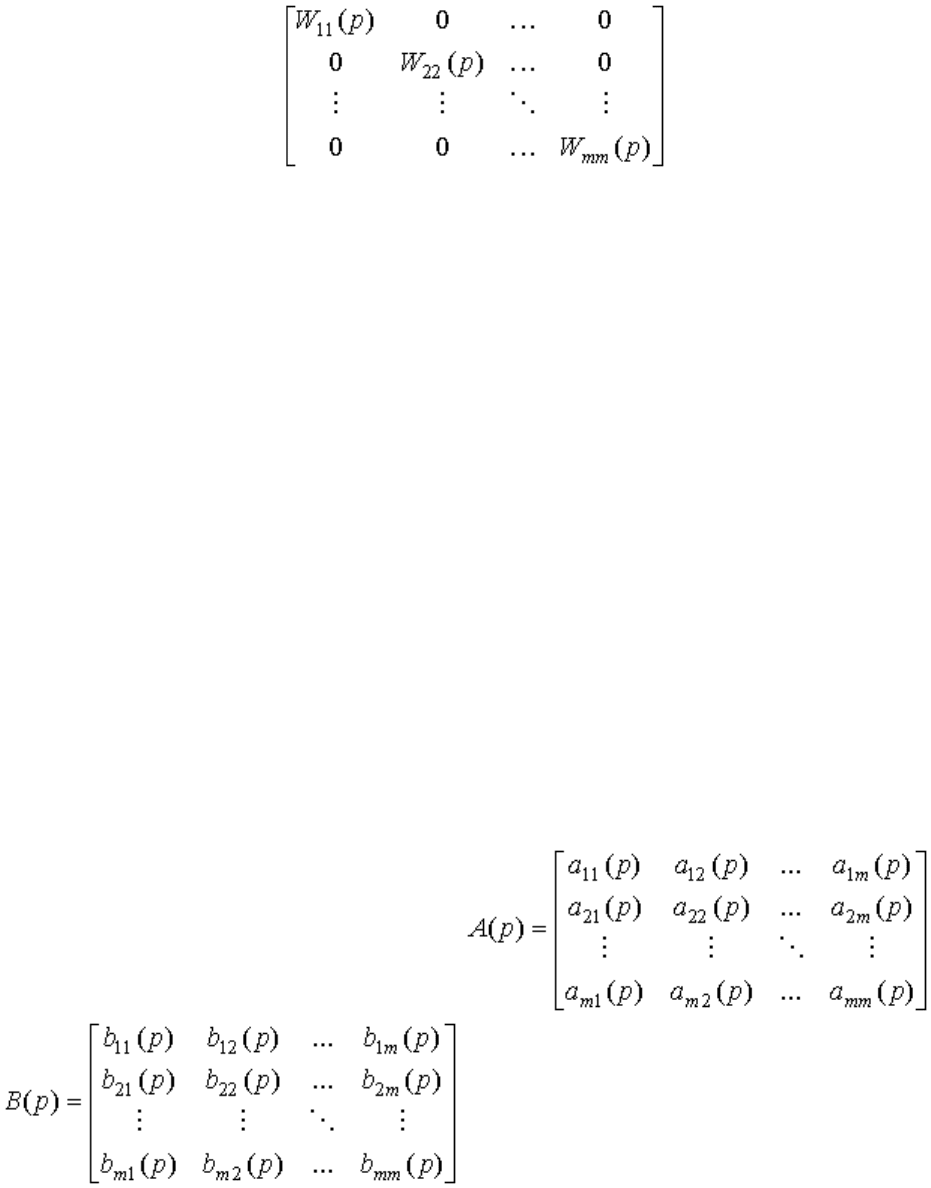
          W(p)=A

-1

(p)B(p)= .

Легко видеть, что в рассматриваемом случае передаточная матрица является диагональной, т.е.

          W(p)=diag{W

(p)}={b

(p)/a

(p)}.

Теперь рассмотрим многосвязную систему, т.е. многоканальную систему со связанными каналами,

описываемую системой операторных уравнений

         

(p)y

+...+a

(p)y

(p)u

+...+b

(p)u

         

(p)y

+...+a

(p)y

(p)u

+...+b

(p)u

[M2m]          . . .

         

(p)y

+...+a

(p)y

(p)u

+...+b

(p)u

Система приводится к векторно-матричной форме [M2m ], где

          ;

и форме [M3m] , где передаточная матрица W(p) определяется выражением

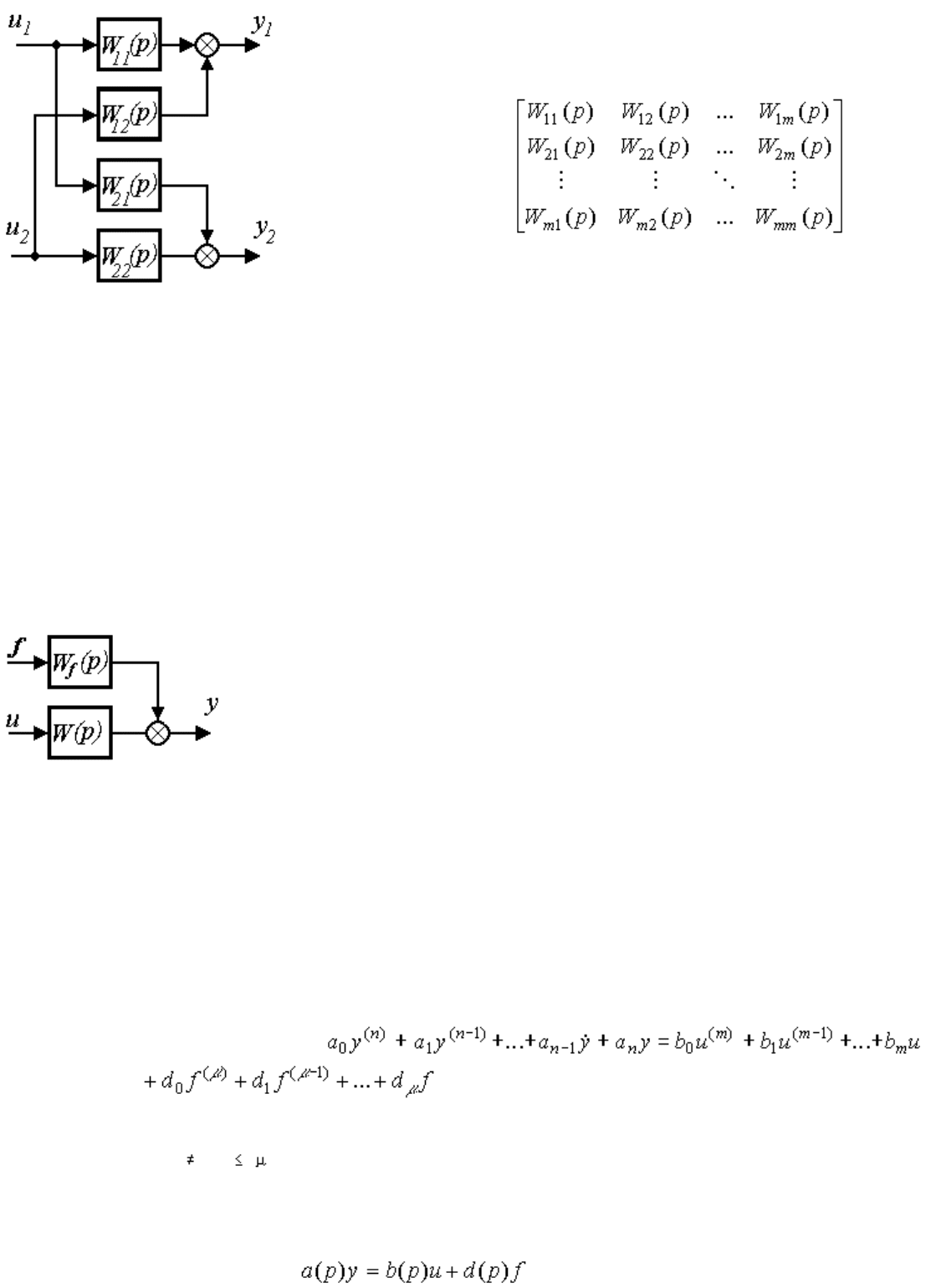
          W(p)=A

-1

(p)B(p)=

Модель [M3m] можно также записать в скалярном виде:

          y

(p)u

+ W

(p)u

+...+W

(p)u

          y

(p)u

+ W

(p)u

+...+W

(p)u

          . . .

          y

(p)u

+ W

(p)u

+...+W

(p)u

Отметим, что диагональные операторы W

(p) относятся к основным каналам , а остальные передаточные

функции W

(p) характеризуют перекрестные связи многоканальной системы.

Для двухканальной многосвязной системы ( m=2) получаем:

          y

(p)u

+ W

(p)u

          y

(p)u

+ W

(p)u

где W

(p), W

(p) - передаточные функции основных каналов системы, а W

(p), W

(p) - передаточные

функции перекрестных связей.

2.1.4. Возмущенная модель системы. Возмущающее воздействие f(t), характеризующее влияние на

объект управления внешней среды (см. п. 1.2), рассматривается как дополнительный входной сигнал. Тогда

линейная модель одноканальной динамической системы принимает вид

[М1f]

где d

-коэффициенты, определяющие влияние на процессы в системе возмущения f(t) и его производных f

(i)

(t), d

, 0 <n. После подстановки операторов дифференцирования p

и соответствующих преобразований

получаем операторную форму модели [M1f]:

[М2f]           ,

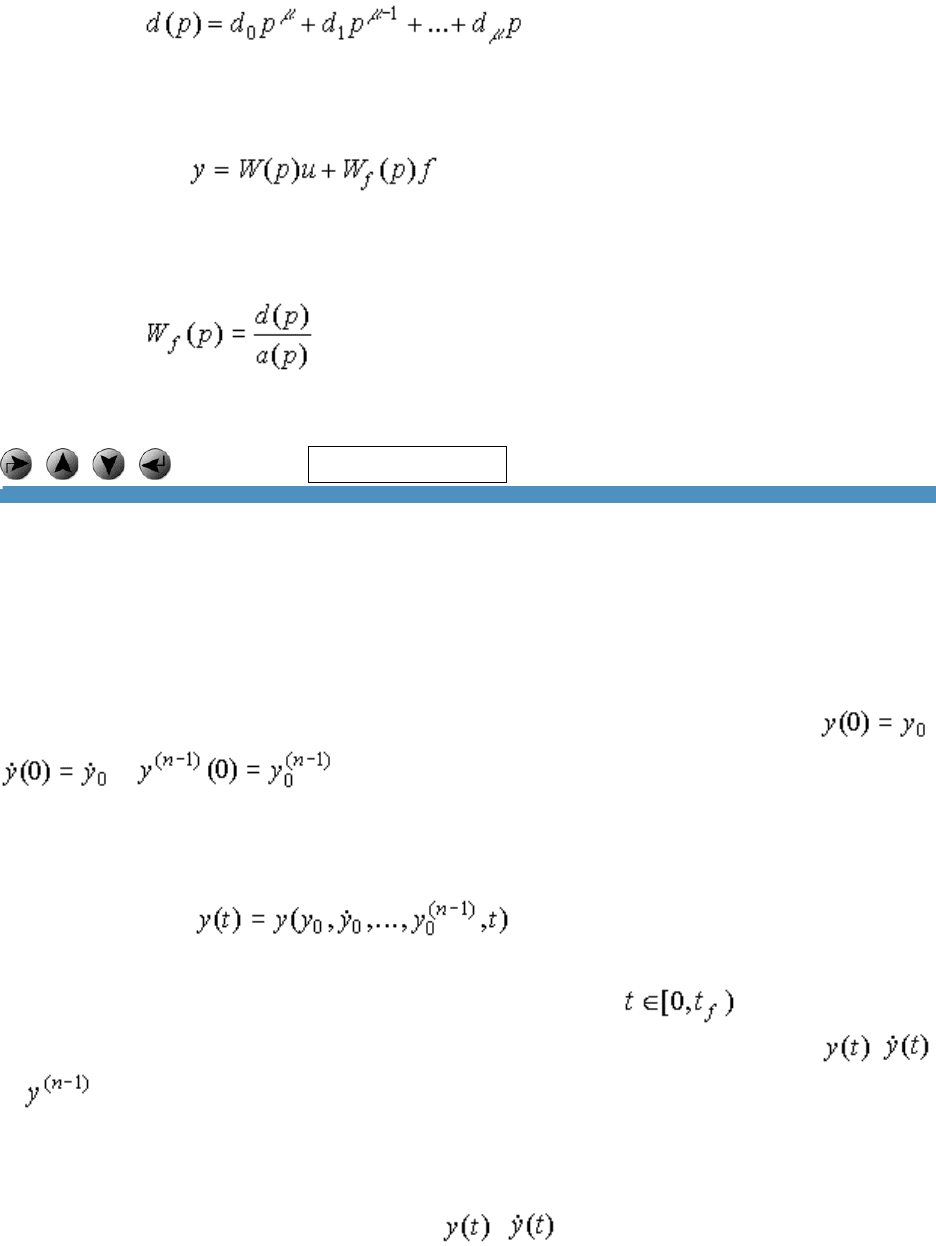
где используется дифференциальный оператор

          .

Явная операторная форма приобретает вид

[М3f]           ,

где

          .

передаточная функция по возмущающему воздействию f(t).

   

Уровень:

Переходные процессы и характеристики моделей

вход-выход

Будем рассматривать линейные стационарные динамические системы, описываемые на интервале времени

[0 , t

), где t

> 0, дифференциальным уравнением [M1] с начальными условиями t(0)=0, ,

,..., и достаточно гладким входным воздействием u(t).

2 .2.1. Переходные процессы. Решением дифференциального уравнения [M1] называется функция

(2.18)           ,

которая при t= 0 удовлетворяет начальным условиям, а для любых уравнению [M1]. С этим

определением тесно связаны понятие фазовых переменных системы, к которым относятся функции, ,

,..., (t) , удовлетворяющие уравнению [M1], и понятие переходного процесса. Переходным процессом

называют процесс изменения во времени различных переменных системы (фазовых и входных переменных,

отклонений и т.д.), в ходе которого система изменяет свое состояние. Переходный процесс может быть получен в

аналитическом или графическом виде. К графическим формам переходного процесса относятся

 временные диаграммы переменных системы: , ,..., u(t ) и т.д.;

 фазовые траектории (или интегральные кривые, см. п. 3.3) .

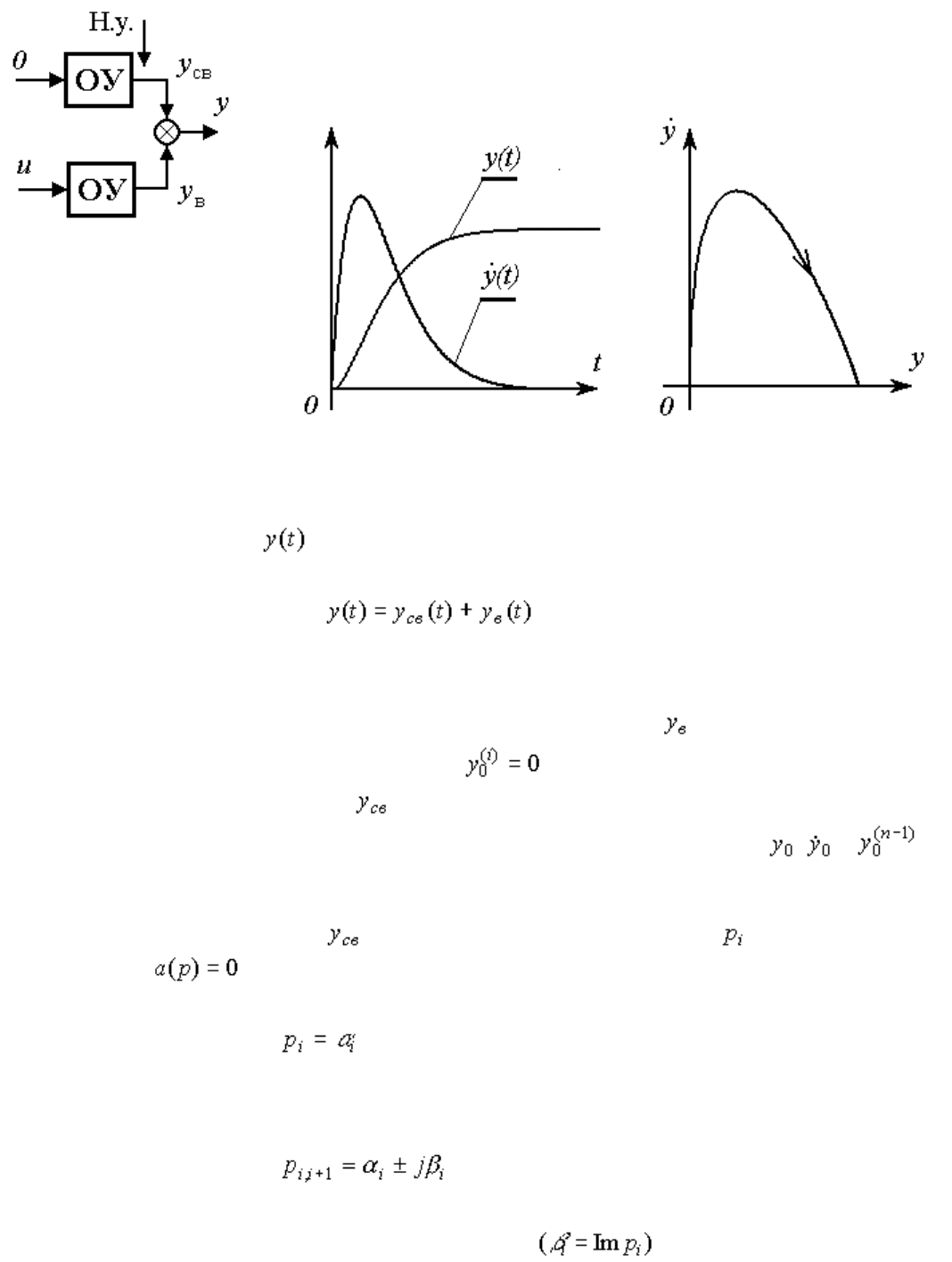
Рис . 2.3 . Переходные процессы: временные диаграммы и фазовая траектория

Решение может быть представлено в виде

(2.19)           ,

т.е. содержит две составляющие. Вынужденная составляющая (t) соответствует переходному процессу

системы [ М1 ] при начальных условиях: и является реакцией системы на входное воздействие u(t).

Свободная составляющая (t), или переходный процесс автономной системы, соответствует решениям

однородного дифференциального уравнения [ М1 a] и зависит от начальных условий , ,...,

2.2.2. Процессы автономной системы. Поведение автономной системы и свободная составляющая

переходного процесса (t ) зависит от полюсов системы, т.е. корней характеристического уравнения

(см. также п. 3.3). Корни принимают вещественные значения

          ,

или представлены комплексно-сопряженными парами:

          ,

где α

=Re p

- вещественная часть корня, - коэффициент мнимой части.

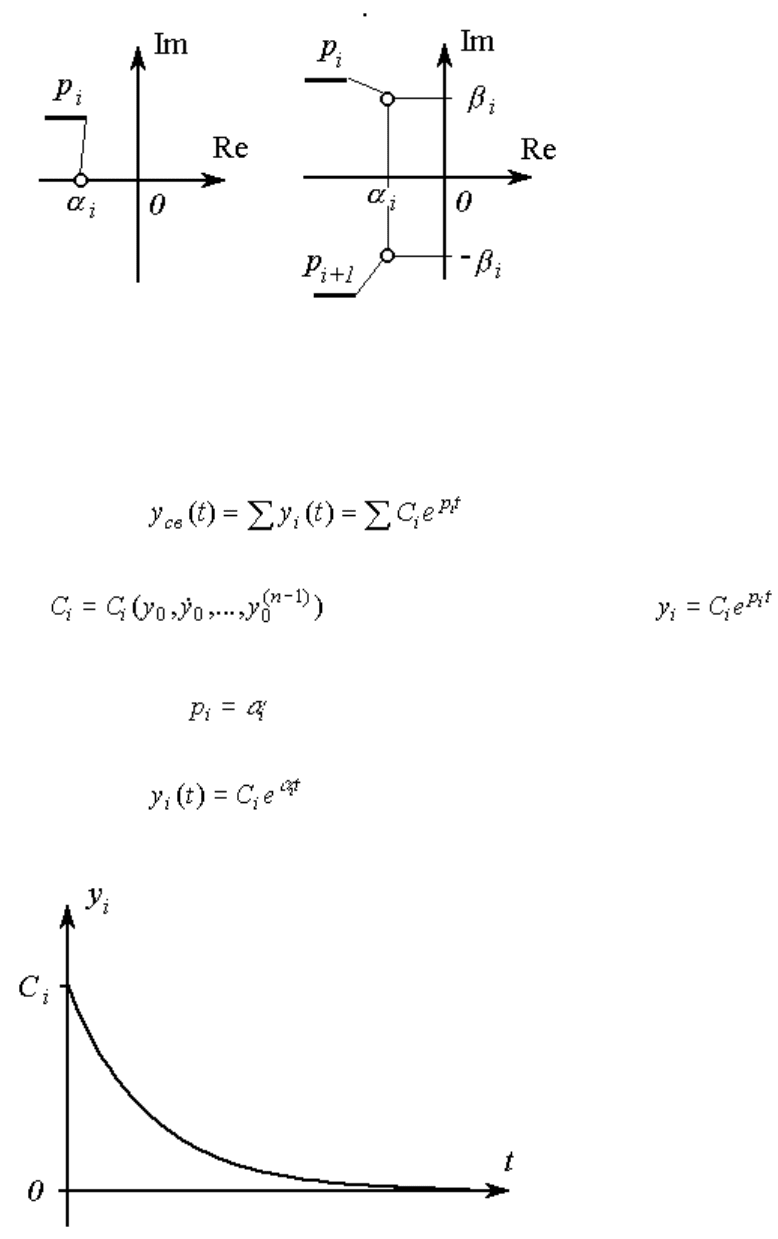
Рис. 2.4. Полюсы системы

Для случая неравных корней свободная составляющая определяется выражением:

(2.20)           ,

где - неопределенные коэффициенты, - свободные

колебания системы, или моды.

Вещественному корню соответствует апериодическая составляющая переходного процесса

(2.21)           ,

Рис. 2.5. Апериодический процесс

Паре комплексно-сопряженных корней характеристического уравнения соответствует колебательная

составляющая

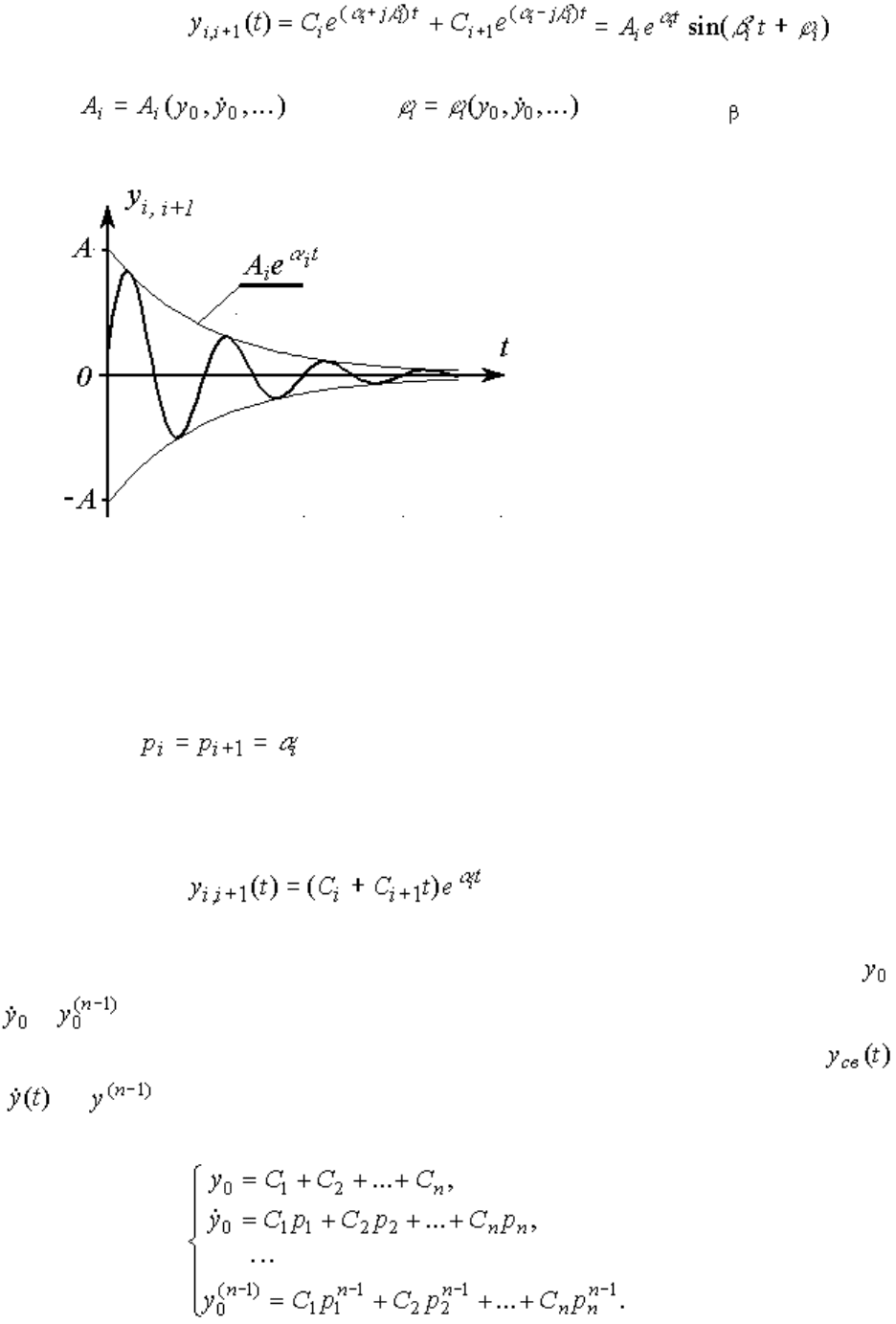
(2.22)           ,

где - амплитуда, - фаза колебаний,

- угловая частота.

Рис. 2.6. Колебательный процесс

Если среди корней характеристического уравнения имеются равные, то выражение (2.20) не справедливо.

Так, паре равных вещественных корней

         

соответствует апериодическая составляющая переходного процесса вида

(2.23)           .

Для нахождения частного решения y

св

(t ), соответствующего заданным значениям начальных условий ,

,..., и значений C

в формуле (2.20) используется метод неопределенных коэффициентов [1]. В

соответствии с методом из формулы (2.20) следует получить общие выражения для фазовых переменных

, ,..., и при t= 0 записать n алгебраических уравнений

(2.24)          