Мироновский Л.А. Моделирование линейных систем Учебное пособие

Подождите немного. Документ загружается.

141

После дифференцирования этих функций с учетом формул,

полученных на предыдущих шагах, приходим к следующей си-

стеме дифференциальных уравнений:

1 2 32 1 4

344 3

11 22

x x xx x x

xxx x

yx yx

= + =- +

= =-



ей отвечает описание (5.5) с матрицами

0210 0

20 0 1 1000 0

0002 0100 0

0 0 20 1

; ;.

é ù éù

ê ú êú

éù

ê ú êú

êú

= ==

ê ú êú

êú

ëû

ê ú êú

ë û ëû

A CX

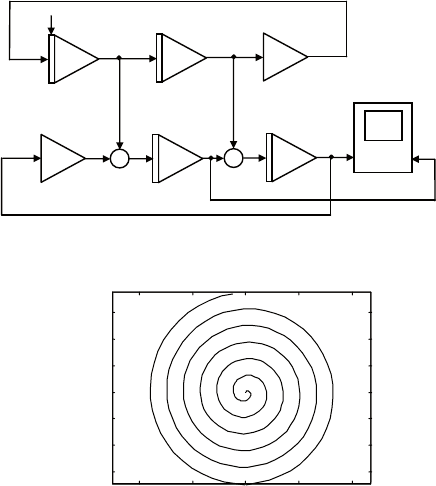
соответствующая схема моделирования приведена на рис. 5.5.

Подавая сигналы

,xxyx==

на входы

,xy

осциллографа, по-

лучим на дисплее график спирали Архимеда (рис. 5.6).

Рис. 5.5. Схема для получения спирали Архимеда

s









s









-40 -20 0 20 40

-30

-20

-10

x=tsin(t), y=tcos(t)

Рис. 5.6. Спираль Архимеда

142

Пример 9. найдем определяющие дифференциальные уравне-

ния в форме (5.5) для функций

2 22 2cos cos , sin sin ,x t ty t t=- =-

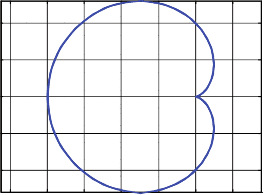
представляющих собой параметрическое описание кардиоиды

(рис. 5.7).

-4 -3 -2 -1 0 1 2

-2

-1

 = 













  = 















Рис. 5.7. Кардиоида

выполняем шаги согласно алгоритму.

Шаг 1. Принимая

2cos ,tϕ =

2sin ,tϕ =

получаем список S

2 22 2( cos , cos , sin , sin ).S tttt=

Шаг 2. выполняем дифференцирование функций

,,ϕϕ

,ϕϕ

2 22

sin , sin ,

cos , cos .

ϕϕ

=- =-



на данном шаге новых функций не появилось, поэтому даль-

нейшего дифференцирования не производим.

Шаг 3. размерность системы (5.5) берется равной 4, равенства

(5.6) имеют вид

cos , sin ,

cos , sin .

x tx t

После их дифференцирования с учетом формул, полученных

на шаге 2, приходим к следующей системе определяющих диф-

ференциальных уравнений:

143

1 3 31

2 44 2

x xxx

x xx x

=- =



Учитывая исходное уравнение, получим

00 1 0

00 0 2

10 0 0

02 0 0

éù

êú

ëû

1 10 0 1

001 1 0

éù

êú

éù

êú

ëû

êú

ëû

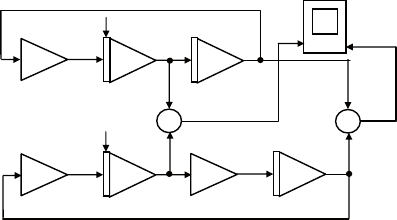
соответствующая схема моделирования изображена на

рис. 5.8.

s













s





s













s



Рис. 5.8. Моделирование кардиоиды

Подавая сигналы х, у на входы осциллографа, получим изо-

бражение кардиоиды (см. рис. 5.7).

Пример 10. Пусть требуется найти определяющие уравнения

в форме (5.5) для функций

sin , cos ,

x t dt y t dt==

òò

представляющих параметрическое описание клотоиды (рис. 5.9).

это кривая, у которой радиус кривизны изменяется обратно

пропорционально длине дуги. она используется как переходная

дуга в дорожном строительстве. если участок дороги имеет фор-

му клотоиды, руль поворачивается равномерно. такая форма

дороги позволяет преодолевать поворот без существенного сни-

жения скорости. другое название клотоиды – спираль корню.

в оптике она используется для расчета дифракции, позволяя

найти амплитуду световой волны в любой точке экрана.

144

для отыскания определяющих уравнений применяем метод

списков.

Шаг 1. Принимая

,,xyϕϕ==

получаем список:

11 2

( ( ), ( )).S ttϕϕ=

Шаг 2. выполняем дифференцирование

(), ()ttϕϕ

по времени:

sin , cos .ttϕϕ==



список S

имеет вид:

2 34

(sin , cos ) ( ( ), ( )).S tt ttϕϕ==

Шаг 3. выполняем дифференцирование функций

:,ϕϕ

22cos , sin .tt ttϕϕ= =-



список S

имеет вид

3 56

( cos , sin ) ( ( ), ( )).S t tt t t tϕϕ==

Шаг 4. выполняем дифференцирование функций

,ϕϕ

выделяем новые компоненты

22 22

sin , cos .tt ttϕϕ==

нетрудно видеть, что дальнейшее дифференцирование приве-

дет к появлению функций вида

cos , sin ,

t tt t

где k зависит от

числа шагов и может неограниченно возрастать. таким образом,

определяющих дифференциальных уравнений вида (5.5) для за-

данных функций не существует, т. е. клотоида не может быть по-

лучена с помощью схемы на сумматорах и интеграторах.

чтобы справиться с возникшей проблемой, расширим класс

допустимых определяющих уравнений и позволим элементам

матрицы А линейно зависеть от времени. тогда при проверке

Рис. 5.9. Клотоида

s s   

s



s



 

 

 



145

функций на линейную зависимость появляется возможность ис-

пользовать не только постоянные, но и линейно изменяющиеся

коэффициенты.

в таком случае функции, полученные на третьем шаге, ока-

зываются линейно зависимыми от функций, полученных на вто-

ром шаге:

5 46 3

,.ttϕ ϕϕ ϕ==

это приводит к системе уравнений

четвертого порядка:

13243 44 3

22,, , ,x x x x x tx x tx= = =- =

  

где обозначено

1234

,,,.x xx yx xx y====



Матрицы этой системы имеют вид

00 1 0 0

00 0 1 1000 0

00 0 2 0100 1

002 0 0

, ,.

é ù éù

ê ú êú

éù

ê ú êú

êú

= ==

ê ú êú

êú

ëû

ê ú êú

ë û ëû

A CX

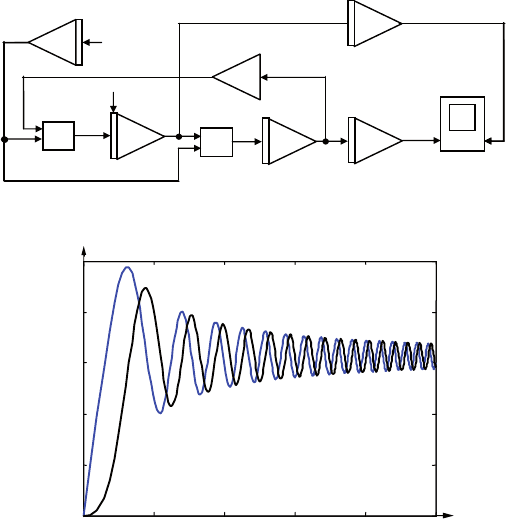
Рис. 5.10. Моделирование клотоиды



 Ë



U





 Y





s







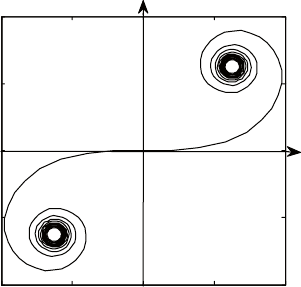
Рис. 5.11. Интегралы Френеля C(t), S(t)

    

 

 

 

 

 

 

YZ

146

заметим, что матрица А нестационарна (ее элементы зави-

сят от t). соответствующая схема моделирования кроме сумма-

торов и интеграторов будет содержать два блока перемножения

(рис. 5.10). графики выходных сигналов схемы х, у приведены

на рис. 5.11; это так называемые интегралы Френеля C(t), S(t).

они асимптотически стремятся к уровню

8 0 62/ ,.π »

зависимость

( ),y fx=

наблюдаемая на осциллографе, пред-

ставляет собой клотоиду (см. правую часть на рис. 5.9). спираль

начинается из начала координат и закручивается вокруг точки

с координатами (0,62; 0,62).

5.6. Моделирование кривых

необходимость воспроизведения плоских и пространствен-

ных кривых возникает при решении многих инженерных за-

дач – изучении фазовых портретов динамических систем, авто-

матической обработке деталей сложных профилей на фрезерных

станках, в системах машинной графики и сАПр, при расчете и

моделировании траекторий движущихся элементов механиче-

ских и робототехнических систем и в ряде других случаев.

5.6.1. Способы задания кривых

в примерах 8, 9, 10 речь шла о моделировании плоских кри-

вых. остановимся на этой задаче подробнее.

Таблица 5.1

Способы задания плоских кривых

координаты

Уравнения

явные неявные параметрические дифференциальные

декартовы

х, у

y = f(x) F(х, у) = 0 x = f

(t), y = f

(t)

,xaxax

ybyby

++=

 

Полярные

ρ, ϕ

ρ = f(θ) F(θ, ρ) = 0 θ = f

(t), ρ = f

(t)

,aa

θθθ

ρρρ

++=

 

натуральные

s, k

k = f(s) F(s, k ) = 0 s = f

(t), k = f

(t)

,s as as

k bk bk

++=

 

Плоские кривые могут задаваться аналитически, графически

или таблично. основные аналитические способы задания пло-

ских кривых (табл. 5.1) различаются используемой системой

147

координат (декартовы, полярные, натуральные), а также видом

уравнений, связывающих эти координаты (явные, неявные, па-

раметрические, дифференциальные).

выбор того или иного способа задания зависит от конкретной

кривой и имеющихся компьютерных средств. например, для за-

дания клотоиды удобнее использовать натуральное уравнение

k = as, для реализации глиссады в бортовом вычислителе само-

лета – определяющее дифференциальное уравнение и т. д.

рассмотрим основные варианты описания плоских кривых.

Уравнение кривой в декартовых координатах. если на пло-

скости введена декартова система координат х, у, то кривая может

быть задана в явной

()y fx=

или в неявной форме

0(, ) .Fxy=

если

(, )Fx y

– многочлен степени n относительно х, у, то гово-

рят об алгебраической кривой порядка n. например, окружность

представляет собой алгебраическую кривую второго порядка,

так как ее уравнение в декартовых координатах имеет вид мно-

гочлена второй степени

22 2

.xyR+=

кривые, не являющиеся алгебраическими, называются транс-

цендентными. Примером такой кривой является логарифмиче-

ская спираль, описываемая уравнением

arctgln( ) .

Уравнение кривой в полярных координатах. если положе-

ние точки на плоскости характеризовать полярным радиусом ρ

(расстояние от полюса до рассматриваемой точки) и полярным

углом ϕ, откладываемым от горизонтальной оси до радиуса, то

уравнение

()fρϕ=

будет задавать кривую в полярной системе

координат.

Переход от декартова уравнения кривой

()y fx=

к полярному

()fρϕ=

осуществляется путем замены координат по формулам

sin , cos .yxρϕ ρϕ==

в частности, приведенные выше уравнения окружности и ло-

гарифмической спирали в полярных координатах будут иметь

вид

,.Re

ρρ==

соответственно, при выполнении обратного перехода исполь-

зуют формулы

arctg,.

ρϕ=+ =

148

Параметрическое задание кривой. если обе координаты, на-

пример декартовы, заданы в виде функций некоторой третьей

переменной t

( ), ( ),x ty tϕψ==

(5.7)

то такое описание называется параметрическим. если t – время,

то формулы (5.7) определяют закон движения точки на плоско-

сти и соответствующая линия называется траекторией. отме-

тим, что одна и та же линия может получиться при различных

уравнениях (5.7), так как законы движения по одной и той же

траектории могут быть различны.

чтобы от параметрического задания перейти к явному уравне-

нию в декартовых координатах, надо из уравнений (5.7) исклю-

чить параметр t, выразив его, например, из первого уравнения

()txϕ

и подставив во второе:

( )

()yxψϕ

или

( ).y fx=

в качестве примера параметрического задания можно приве-

сти параметрическое описание окружности

cos , sin ,xR t yR t==

а также параметрическое представление логарифмической спи-

рали

cos , sin .

xe t ye t==

в последнем случае для перехода к декартовым координатам

удобно рассмотреть выражения

,xy+

а также

что приво-

дит к уравнению

arctgln( ) .

Натуральное уравнение кривой. с геометрической точки зре-

ния кривую удобно задавать уравнением, связывающим кривизну

кривой k в каждой точке с ее длиной s до этой точки (отсчет длины

ведется от некоторой фиксированной точки на кривой). Получаю-

щееся уравнение

()ksϕ=

не зависит от выбора системы координат

и поэтому называется натуральным уравнением кривой.

например, известно, что кривизна окружности постоянна и

обратно пропорциональна ее радиусу. следовательно, натураль-

ное уравнение окружности имеет вид k = 1/R.

натуральное уравнение логарифмической спирали имеет вид

1/.ks=

таковы основные способы задания плоских кривых. для про-

странственных кривых часто используется описание в прямо-

угольных декартовых координатах. в этом случае кривая мо-

149

жет быть задана как линия пересечения двух поверхностей, т. е.

как совокупность точек, координаты которых отвечают системе

уравнений

00(,,) , (,,) .F xyz F xyz==

Широко применяется также параметрический способ задании

пространственных кривых

1 23

( ), ( ), ( ).x ft y ft z ft= ==

(5.8)

в этом случае кривая получается как траектория движущей-

ся точки. так, параметрические уравнения прямой в простран-

стве имеют вид

11 22 33

, ,.x a bt y a bt z a bt=+ =+ =+

Пространственную кривую можно задавать также в сфериче-

ских координатах. этот способ является пространственным ана-

логом полярных координат. точка характеризуется здесь радиу-

сом ρ и двумя углами ϕ и θ. например, местоположение точки на

поверхности земли определяется долготой и широтой.

во всех программных математических пакетах имеются сред-

ства для построения графиков кривых. как правило, они ориен-

тированы на явное задание кривой в декартовой или полярной

системах координат, либо на параметрическое представление.

в частности, в пакете MATLAB для этих целей служат коман-

ды plot, plotyy, plot3; в пакете MAPLE – команды plot, smartplot.

неявное задание кривых поддерживается только в наиболее

мощных математических системах: в пакете MATLAB для этого

предназначены команды ezplot и ezplot3, в пакете MAPLE – ко-

манда implicitplot.

в ряде случаев, например в специализированных вычисли-

тельных устройствах (бортовые компьютеры, станки с программ-

ным управлением), кривые удобно задавать определяющими

дифференциальными уравнениями, подобно тому, как это было

сделано в предыдущем разделе для спирали Архимеда и клотои-

ды. ниже описывается применение этого подхода для наиболее

известных плоских и пространственных кривых.

5.6.2. Моделирование плоских кривых

Алгебраические кривые второго порядка. самыми простыми

плоскими кривыми являются алгебраические кривые перво-

го порядка, т. е. прямые

.y ax b=+

далее идут алгебраические

кривые второго порядка: эллипс, гипербола и парабола. их ка-

150

нонические уравнения в декартовых координатах имеют вид со-

ответственно

22 22

11, ,.

xy xy

y px

ab ab

+= -= =

(5.9)

эти кривые встречаются и используются во многих областях

науки и техники: в геометрии (как сечения цилиндров и кону-

сов), оптике (при построении отражательных поверхностей), в

баллистике (параболы безопасности), в метрологии (эллипсы по-

грешностей), в теории управления (эллипсы управляемости и на-

блюдаемости).

При решении прикладных задач возникает необходимость

отображения кривых на экране дисплея. для решения этой про-

блемы воспользуемся динамическим способом, в основе которого

лежит получение определяющих дифференциальных уравнений

и построение соответствующих схем моделирования.

чтобы применить его для кривых (5.9), перейдем к их параме-

трическому представлению

cos , ,

sin , ,

xa t xat

yb t ybt

y pt

ìì

ïï

í íí

ï ïï

îî

(5.10)

Получение определяющих дифференциальных уравнений в

данном случае не представляет труда. соответствующие схемы

моделирования приведены на рис. 5.12.

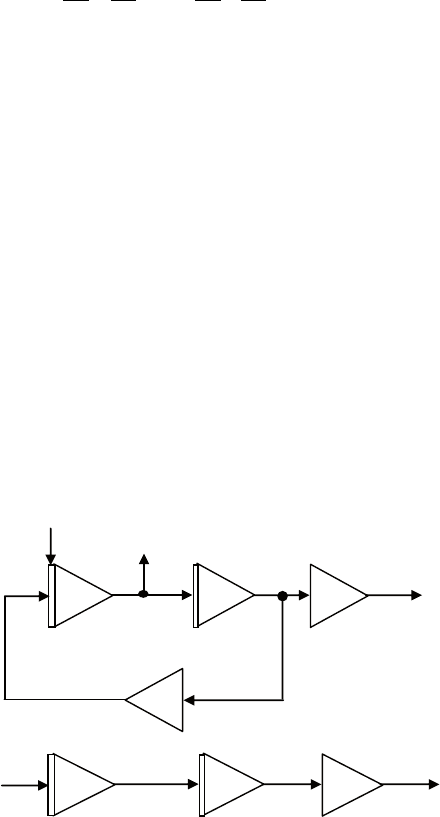
Рис. 5.12. Получение канонических кривых второго порядка:

эллипса (а) и параболы (б)

Í

Q





Í



CB



б)

а)