Мироновский Л.А. Моделирование линейных систем Учебное пособие

Подождите немного. Документ загружается.

131

а)

[ ]

10 1

02 1

,, ,

é ù éù

ê ú êú

= ==

ê ú êú

ë û ëû

A bc

б)

[ ]

12 1

34 0

,, ,

é ù éù

ê ú êú

=- = =

ê ú êú

ë û ëû

A bc

в)

[ ]

01 1

10 1

,, ,

é ù éù

ê ú êú

= ==

ê ú êú

ë û ëû

A bc

г)

[ ]

12 1

04 0

,, .

é ù éù

ê ú êú

=- = =

ê ú êú

ë û ëû

Acb

9. найти параллельную и последовательную канонические

формы для систем с передаточной функцией:

а)

pp++

б)

;

pp++

в)

;

г)

10. найти вторую каноническую форму кауэра и контурное

представление скалярной системы для систем с передаточными

функциями из упражнения.

132

5. МОДЕЛИРОВАНИЕ ФУНкЦИЙ ВРЕМЕНИ

в ряде случаев при компьютерном моделировании возникает

необходимость генерировать функции времени, заданные чис-

ленно, графически или аналитически. в качестве примеров мож-

но указать:

– получение возмущающих функций и воспроизведение пере-

менных коэффициентов при моделировании дифференциальных

уравнений;

– получение тестовых воздействий для исследования систем

автоматического управления;

– реализацию функций для нахождения корней трансцен-

дентных или алгебраических уравнений;

– получение графиков плоских и пространственных кривых.

5.1. компьютерная реализация функций времени

существует несколько способов компьютерной реализации

функций – табличное представление, разложение в ряд, ис-

пользование порождающих дифференциальных или разностных

уравнений. они отличаются друг от друга точностью, быстродей-

ствием, программными и аппаратурными затратами.

Табличный способ. в данном случае функция задается своими

значениями на некотором наборе точек. таким образом, исхо-

дные данные представляют собой таблицу чисел. для обеспече-

ния достаточной точности необходимо иметь значительное число

точек. это приводит к увеличению размера таблицы и, соответ-

ственно, возрастанию требуемого объема оперативной памяти

(дискового пространства), однако данный способ обладает макси-

мальным быстродействием и производительностью.

Разложение в ряды. исходной информацией здесь является

аналитическое представление функции. это позволяет предста-

вить ее в виде ряда, т. е. суммы некоторых слагаемых. напри-

мер, для вычисления экспоненты можно использовать разложе-

ние в ряд тейлора:

123

...,

!!!

ttt

e =+ + + +

что потребует хранения в памяти не таблицы функции, а только

первых коэффициентов ряда (1, 1, 1/2, 1/6, 1/24, …).

133

это приводит к экономии памяти (хранятся только несколько

коэффициентов разложения), однако необходимо дополнитель-

ное время и вычислительные ресурсы на выполнение алгоритма.

заметим, что данный способ используется в большинстве кар-

манных калькуляторов.

Построение определяющего дифференциального уравнения.

еще большей экономии памяти можно достичь, если хранить

в ней только коэффициенты дифференциального или разностно-

го уравнения, решением которых является данная функция. та-

кой способ удобен, в частности, для бортовых вычислительных

машин, когда аргументы функций, например время или углы,

монотонно изменяются во время полета. решая соответствующее

дифференциальное уравнение в бортовом компьютере, постепен-

но, точка за точкой, получают искомые значения функций. эта

идея лежит в основе динамического способа, который и рассма-

тривается далее.

Проще всего этим способом генерировать функции, которые

являются решениями линейных дифференциальных уравнений

с постоянными коэффициентами. к таким функциям относятся

, , sin , cos

et t t

ωω

и их комбинации. задача сводится к отыска-

нию определяющего дифференциального или разностного урав-

нений

1 10

() ( )

y a y ay ay

+ ++ + =…

(5.1)

1 1 11 0

nk n nk k k

y a y ay ay

+ - +- +

+ ++ + =…

(5.2)

для которых они являются решением.

существует несколько методов построения определяющих

уравнений для заданных функций. рассмотрим четыре из них:

метод последовательного дифференцирования, метод характери-

стического полинома, использование определителя вронского и

метод списков.

5.2. Метод последовательного дифференцирования

Процедура поиска определяющего уравнения этим методом

сводится к вычислению некоторого числа производных исходной

функции, на основании которых можно составить линейное диф-

ференциальное уравнение.

Пусть задана функция y = f(t) и требуется найти дифферен-

циальное уравнение (5.1), решением которого она является. для

134

отыскания этого уравнения рассмотрим наряду с функцией y(t)

ее производные

( ), ( ), ( ), ,yt yt yt

  

…

причем дифференцирование бу-

дем выполнять до тех пор, пока очередная функция не окажется

линейной комбинацией предыдущих:

01 1

() ( )

() () () ().

y t a yt ayt a y t

= + ++



…

найденное соотношение и будет представлять собой искомое

дифференциальное уравнение.

для проверки системы функций, полученных после очеред-

ного дифференцирования, на линейную зависимость можно ис-

пользовать стандартные математические критерии: вычисление

определителя грама, отыскание сингулярных чисел, определе-

ние ранга и т. п.

Пример 1. найдем дифференциальное уравнение, имеющее

своим решением функцию

() .

y t Ae

α-

Решение. дифференцируя, получаем функцию

() ,

yt A e



пропорциональную исходной. следовательно, определяющее

уравнение имеет вид

0.yyα+=



решением этого уравнения является

() .

y t Ce

α-

для того

чтобы обеспечить равенство С = А, необходимо задать начальное

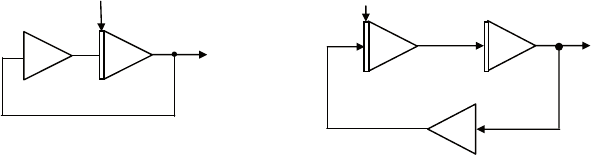
условие y(0) = A. соответствующая схема моделирования пока-

зана на рис. 5.1.

Пример 2. Пусть требуется получить функцию y(t) = sinkt.

Решение. для отыскания определяющего уравнения дважды

дифференцируем исходную функцию:

cos , sin .y k ty k t= =-

 

отсюда получаем, что искомое уравнение имеет вид

00, ,.y ky y y k+= = =

 

схема моделирования показана на рис. 5.2. ее часто использу-

ют в технике в качестве генератора гармонических колебаний.

Рис. 5.1. Получение

функции

α-



sA



Ë

Í



( )

y t Ae

A-

Рис. 5.2. Получение функций

sinkt и coskt

135

Пример 3. найдем определяющее дифференциальное уравне-

ние для функции y(t) = te

Решение. дважды дифференцируя, получаем

y e te=+ =



t tt t

ye te e y ye y=+ =+ =+

  

разность двух последних равенств дает

yy yy-=-

  

или

20.y yy- +=

 

это и есть искомое дифференци-

альное уравнение.

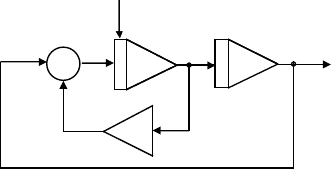
Рис. 5.3. Получение функции



Ë







схема его моделирования показана на рис. 5.3.

5.3. Метод характеристического полинома

в этом методе используется соответствие между корнями ха-

рактеристического полинома и решениями дифференциального

уравнения.

исходная функция

()yt

представляется в виде суммы элемен-

тарных слагаемых. По их виду с помощью табл. 2.1 (см. разд.

2) определяются корни соответствующего характеристического

полинома и составляется характеристическое уравнение вида

(p – p

)(p – p

) … (p – p

) = 0. от него легко перейти к дифферен-

циальному уравнению

1 10

() ( )

... ,

y a y ay ay

+ ++ + =



где коэффициенты a

рассчитываются по известным корням р

с помощью формул виета

0 12 1 1 2

1 … ,… …( ) , ( ).

nn n

a pp p a p p p

= - =- + + +

Пример 4. Пусть требуется воспроизвести функцию

2( ) sin cos .

yt e t t t

2( ) sin cos .

yt e t t t

здесь первому слагаемому соответствует пара

комплексных корней

,pj=- ±

а второму – кратные чисто

мнимые корни

34 56,,

.pp j= =±

характеристическое уравнение

имеет вид

136

( )( )( )( )( )( )

12 12 0p jp jpjp jpjp j+- ++ -+-+=

или после раскрытия скобок

65432

2 4 4 5 2 20.pppppp++++++=

в результате получим следующее дифференциальное уравне-

ние

65432

2 4 4 5 2 20

() () () () ()

.y y y y y yy

++++++=

начальные условия находим как значения исходной функ-

ции и пяти ее производных при t = 0. схема моделирования бу-

дет представлять цепочку из шести интеграторов, охваченную

обратными связями.

другой вариант заключается в раздельном рассмотрении сла-

гаемых исходной функции и получении дифференциального

уравнения для каждого из них.

характеристические уравнения для первого и второго слагае-

мых имеют вид соответственно:

2 42

2 20 2 10,.pp pp+ += + +=

это приводит к двум определяющим дифференциальным

уравнениям

222 11

220 2 0

()

,.yyy y yy

¢¢ ¢ ¢¢

+ + = + +=

искомая функция y(t) получается как сумма y(t) = y

(t) +

+ y

(t). схема моделирования будет содержать два параллельных

фрагмента (второго и четвертого порядка).

рассмотренный метод прост, но применим только для вос-

произведения функций, которые являются решениями линей-

ных дифференциальных уравнений с постоянными коэффици-

ентами.

Процедура построения определяющих разностных уравнений

выглядит аналогично, только операция дифференцирования за-

меняется сдвигом функции на такт дискретного времени.

Пример 5. найдем определяющее разностное уравнение вида

(5.2) для функции y(t) = te

–t

Решение. Перейдем к дискретному времени t = kh, k = 0, 1,

2, …. требуется получить функцию вида

( ).

y c c kh e

следовательно, характеристический полином разностного урав-

137

нения должен иметь кратный корень

zze

восстанавли-

вая полином по корням, получаем

2( )( ) .

zzzz z e ze

- - =- +

ему соответствует разностное уравнение второго порядка

kkk

y ey e y

- +=

c начальными условиями

0,.

y y he

При h = 0,1 оно принимает вид

2 1 01

1 81 0 819 0 0 0 0904837, , ,,, .

kk k

y y yy y

- + ===

5.4. Метод определителя Вронского

этот метод удобно применять, когда требется воспроизвести

одну из функций времени f

(t), …, f

(t) или их линейную комби-

нацию.

определитель

()

¢¢

…

………

…

(5.3)

называется определителем вронского для функций f

(t), …,

(t).

в курсе дифференциальных уравнений доказывается, что

если определитель вронского W(t) не равен нулю ни при каком t,

то уравнение

()

() ()

n nn

f fy

¢ ¢¢

…

……… …

…

(5.4)

имеет своими решениями функции f

(t), …, f

(t).

138

Пример 6. Пусть нужно воспроизвести систему функций 1,

t, t

. определитель вронского (5.3) этих функций отличен от

нуля:

012 2

00 2

() .

Wt t==

в данном случае он находится без труда, в более сложных слу-

чаях определитель вронского можно вычислить в пакете MAPLE

с помощью команды wronskian.

определяющее дифференциальное уравнение (5.4) имеет вид:

012

00 2

00 0

tt y

¢¢

¢¢¢

отсюда

0.y

¢¢¢

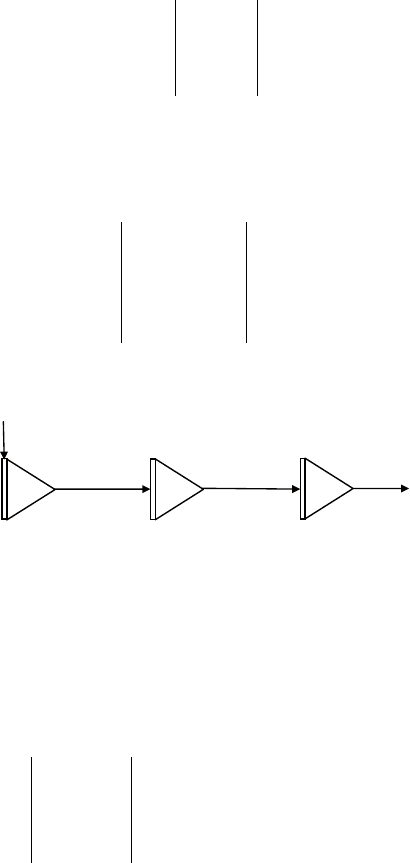
схема моделирования этого уравнения пока-

зана на рис. 5.4.

Рис. 5.4. Схема получения функций 1, t, t



Z





если на интеграторах установить начальные условия

00 0

001,,,yy y== =

 

то на выходах интеграторов будут воспро-

изводиться функции 1, t, 0,5t

, которые совпадают с требуемы-

ми с точностью до постоянных коэффициентов.

Пример 7. найдем дифференциальное уравнение, решением

которого являются функции

sh,.

e t

строим для этих функций

определитель (5.4) и раскрываем его:

( )

ch ch sh 0

() .

e ty

e t y e t ty y

e ty

=- + - =

 



139

отсюда определяющее дифференциальное уравнение имеет

вид

0.yy-=



для получения функции e

надо взять начальные

условия

1,yy==



а для функции sht – начальные условия

= 0,

1.y =



5.5. Метод списков

в некоторых случаях необходимо воспроизвести одновремен-

но несколько функций времени y

= f

(t), …, y

= f

(t). исполь-

зование описанных выше способов приводит к получению не-

скольких определяющих дифференциальных уравнений разных

порядков. однако размерность модели в смысле числа исполь-

зуемых интеграторов или элементов задержки может оказаться

завышенной.

для получения модели минимальной размерности будем ис-

кать ее описание в виде системы определяющих дифференциаль-

ных уравнений первого порядка

, ,,==



X AX Y CX X

(5.5)

где Х – вектор переменных состояния; Y – вектор выходных сиг-

налов, реализующих заданные функции времени; Х

– вектор

начальных условий, А и С – постоянные матрицы, подлежащие

определению.

Алгоритм получения системы (5.5) минимального порядка,

обеспечивающей выполнение равенств y

= f

(t), …, y

= f

(t),

состоит в следующем.

Шаг 1. составляем список S

линейно независимых элемен-

тарных функций

1( ), , ,

ti qϕ =

через которые линейно выража-

ются заданные функции f

(t), …, f

(t). в частности, можно при-

нять ϕ

= f

(t), …, ϕ

= f

(t).

Шаг 2. дифференцируем функции списка S

, раскрываем вы-

ражения

… (), , ()

ttϕϕ

и составляем список S

новых функций

1( ), , ,

tiq rϕ =+

появившихся после дифференцирования и не

выражающихся линейно через функции списка S

Шаг 3. дифференцируем функции списка S

, раскрываем вы-

ражения

… (), , ()

ttϕϕ

и составляем список S

новых функций

1( ), , ,

tir sϕ =+

появившихся после этого дифференцирования и

не выражающихся линейно через функции списков S

и S

Шаги, аналогичные шагам 2 и 3, повторяются до тех пор,

пока окажется, что после очередного дифференцирования на k-м

140

шаге новых функций, линейно независимых от предыдущих, не

появилось. если такого шага не наступит, то это означает, что си-

стемы определяющих дифференциальных уравнений вида (5.5)

для заданных функций не существует.

Шаг k + 1. размерность системы (5.5) берется равной общему

числу n функций

( ),

tϕ

вошедших в списки S

, S

, …, S

. все эти

функции линейно независимы, чем гарантируется минимальное

число уравнений в системе. сами эти функции принимаются за

переменные состояния системы (5.5)

= ϕ

(t), x

= ϕ

(t), …, x

= ϕ

(t). (5.6)

дифференцируя равенства (5.6) и выражая их правые части

через x

(t), …, x

(t) {это возможно, так как они должны линейно

зависеть от

( ), , ..., ( )

tE tϕϕ

}, получим систему дифференциаль-

ных уравнений



X AX

Матрицу С находим, выражая функции

(t) через

( ), ..., ( ).

ttϕϕ

компоненты вектора начальных усло-

вий Х

получаем из равенств (5.6) при t = 0.

Проиллюстрируем описанный алгоритм на примере.

Пример 8. Пусть требуется найти определяющие уравнения

в форме (5.5) для функций

sin , cos ,xt t yt t==

представляю-

щих параметрическое описание спирали Архимеда.

Решение. выполняем шаги согласно алгоритму.

Шаг 1. Принимая

,,xyϕϕ==

получаем список S

1 12

( sin , cos ) ( ( ), ( )).S t tt t t tϕϕ==

Шаг 2. выполняем дифференцирование функций

:(), ()ttϕϕ

( ) sin cos , ( ) cos sin .t tt t t tt tϕϕ=+ =-

новыми функциями здесь являются sin t и cos t, поэтому

2 34

(sin , cos ) ( ( ), ( )).S tt ttϕϕ==

Шаг 3. выполняем дифференцирование функций

:(), ()ttϕϕ

( ) cos ,ttϕ =

( ) sin .ttϕ =-

на данном шаге новых функций не появилось, поэтому даль-

нейшее дифференцирование не требуется.

Шаг 4. размерность системы (5.5) берем равной 4, при этом

равенства (5.6) имеют вид

1 2 34

sin , cos , sin , cos .x t tx t tx tx t= = ==