Мироновский Л.А. Моделирование линейных систем Учебное пособие

Подождите немного. Документ загружается.

121

такой записи отвечает параллельное соединение n апериоди-

ческих звеньев (рис. 4.22).

в случае комплексных и кратных корней структура парал-

лельной реализации усложняется, в ней могут появляться зве-

нья второго и более высоких порядков. в пакете MATLAB па-

раллельная каноническая реализация строится командой canon

с опцией «modal».

Последовательная реализация получается путем представле-

ния передаточной функции в виде произведения элементарных

сомножителей. в случае вещественных нулей и полюсов систе-

мы она имеет вид

12 1

……() .

mm n

pzpz pz

Qp k

pppp pppp pp

-- -

-- - - -

(4.20)

такой записи передаточной функции отвечает последова-

тельное соединение звеньев, показанное на рис. 4.23 для случая

1.mn=-

При наличии комплексных нулей и полюсов разложение

(4.20) будет содержать сомножители второго порядка, в пакете

MATLAB это разложение получается командой zpk.

Пример 12. найдем параллельную и последовательную кано-

нические реализации передаточной функции

19 90

() .Qp

для этого представим ее в виде суммы и произведения элемен-

тарных дробей

1 1 11

9 10 9 10

() .Qp

p p pp

=- =

+ + ++

Рис. 4.22. Параллельная

реализация





V



V

p p-

p z

p p

p z

p p



Рис. 4.23. Последовательная реализация

122

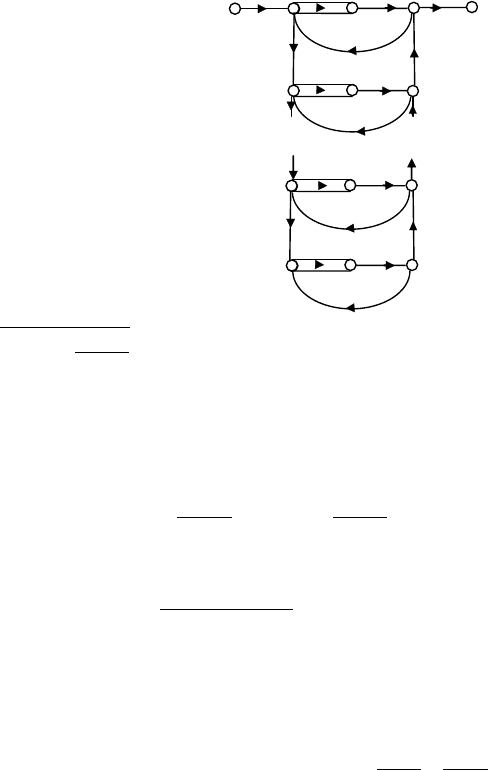
сигнальные графы соответствующих схем моделирования

приведены на рис. 4.24.

Цепные канонические формы. ряд канонических реализаций

основан на разложении передаточной функции в цепные дро-

би. они применяются в математике и вычислительной технике

для приближенного представления чисел и функций, в теории

электрических цепей – при анализе и синтезе лестничных схем

и других областях. Представляя передаточную функцию в виде

некоторой цепной дроби и строя соответствующую схему моде-

лирования, можно получить канонические реализации Шварца,

рауса и кауэра.

стандартный способ получения цепных дробей – алгоритм

евклида. согласно ему сначала выделяется целая часть дроби

(числовой или дробно-рациональной), остаток «переворачива-

ется», вновь выделяется его целая часть и т. д. в случае пере-

даточной функции

() ()/ ()Qp Bp Ap=

деление полиномов

()Ap

на

()Bp

можно начинать со старших или младших степеней,

в зависимости от этого будем получать первую или вторую форму

кауэра.

для второй формы кауэра получаем цепную дробь, содержа-

щую 2n ступенек вида:

()

() ,

()

…

где

αβ

– числовые коэффициенты; n – порядок передаточной

функции.

Рис. 4.24. Сигнальные графы для примера 12



s



s



s



s



б)

а)

123

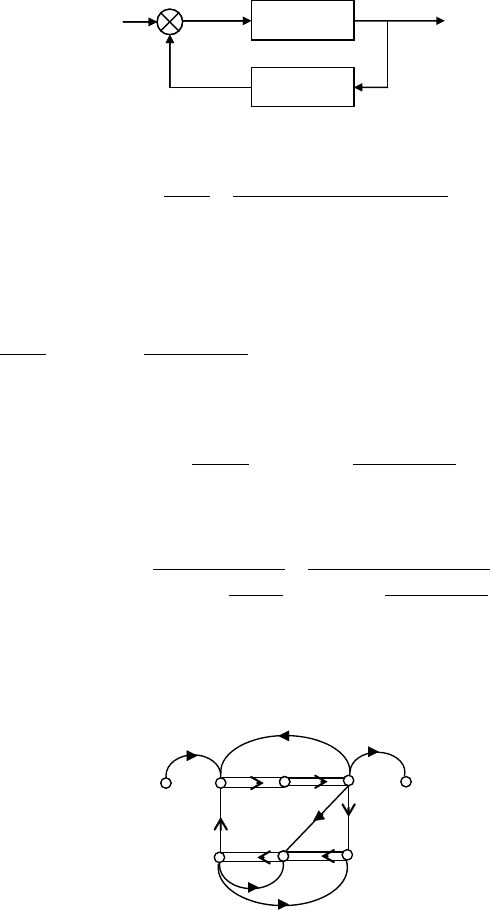
такой записи отвечает регу-

лярная структурная реализация,

сигнальный граф которой приве-

ден на рис. 4. 25.

отметим еще одну канони-

ческую форму, получаемую в

результате выполнения только

одного шага алгоритма евклида.

это так называемая контурная

каноническая форма.

для ее построения передаточ-

ная функция (4.19) представля-

ется в виде

() ,

()

где полиномы А

(р) и В

(р) представляют собой целую часть и

остаток от деления А(р) на В(р):

A(p)/ B(p) = А

(p) + В

(p)/ В(p).

отсюда, обозначив

()

() , () ,

() ()

Qp Qp

A p Bp

получаем

контурное представление скалярной системы

()

() .

() ()

Q pQ p

(4.21)

Формуле (4.21) соответствует встречно-параллельное соеди-

нение систем с передаточными функциями Q

(р) и

()Qp

, пока-

занное на рис. 4.26.

таким образом, для получения контурного представления

надо записать обратную передаточную функцию

1 ()

() ()

Qp Bp

выделить в ней целую часть – полином А

(р) и остаток – полином

(р). это можно сделать всегда, и притом единственным обра-

зом. в пакете MATLAB для этого удобно использовать команду

deconv.

Пример 13. найдем контурное представление системы, задан-

ной следующей передаточной функцией:

Рис. 4.25. Симметричная цеп-

ная каноническая форма







c 

Os

Os



Os





124

432

2 3 21

()

Bp p p

pppp

+ + ++

в данном случае n = 4, m = 2.

Решение. для получения контурного представления выпол-

няем один шаг алгоритма евклида:

6 11

2 2 6 11

()

, () , () .

()

Ap p

p Ap p Bp p

=-+ =- =+

выписываем передаточные функции Q

(р) и

:()Qp

1 6 11

2 25

() , () .

Qp Qp

p pp

- ++

следовательно, искомое представление имеет вид:

6 11

() .

()

Bp p

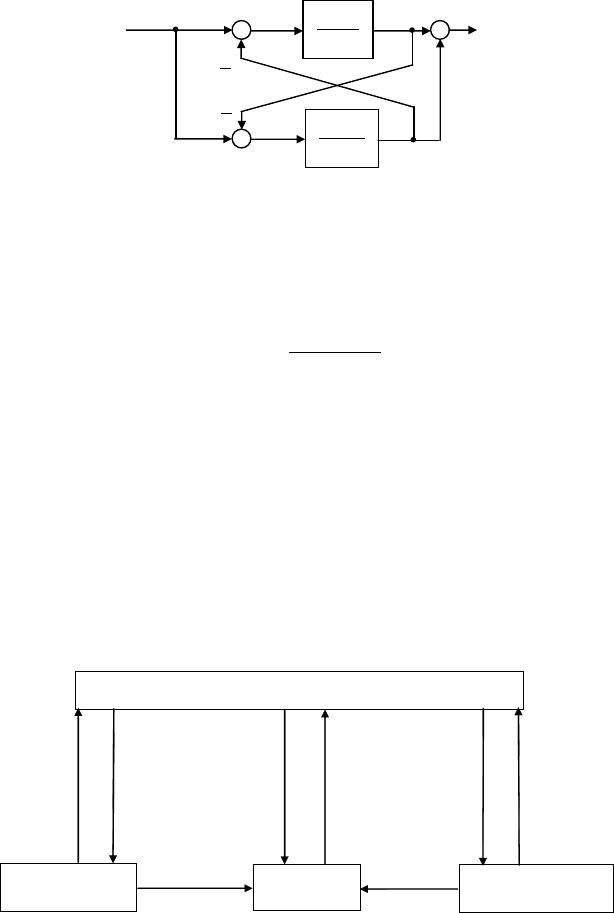
на рис. 4.27 показан сигнальный граф, отвечающий такой за-

писи передаточной функции.

Рис. 4.26. Контурное представление передаточной функции



Q



Q



Q



Q

Z

Рис. 4.27. Контурная каноническая форма системы для примера 13



[





[





s

s



s

s



[









125

он содержит единственный прямой путь от входа до выхода

длины n – m = 2.

нулевой полином исходной системы совпадает с характери-

стическим полиномом нижней части сигнального графа и равен

25,pp++

его корни – это передаточные нули исходной систе-

мы.

отметим два свойства контурного представления. во-первых,

в нем явно выделяется подсистема

( ),Qp

отвечающая за запаз-

дывание ее выходного сигнала относительно входного.

во-вторых, полюсы подсистемы

()Qp

равны передаточным

нулям исходной системы. тем самым исследование нулей ис-

ходной системы сводится к исследованию полюсов вспомога-

тельной системы меньшего порядка. благодаря этому контурное

представление полезно для отыскания передаточных нулей ис-

ходной системы и для расчета ее нулевых режимов, т. е. ненуле-

вых входных сигналов f(t) и согласованных с ними начальных

условий, при которых выходной сигнал проверяемой системы

тождественно равен нулю. все множество нулевых режимов мо-

жет быть получено путем экспериментов с подсистемой

( ),Qp

причем функции f(t) – это множество выходных сигналов систе-

мы

( ),Qp

получаемых при ее свободном движении из различных

начальных условий.

Сбалансированные реализации. особый класс канонических

реализаций образуют сбалансированные представления. они не

отличаются простотой структурной реализации и для них не-

известен какой-нибудь специальный вид записи передаточной

функции, как это имело место для предыдущих канонических

форм. главная отличительная черта сбалансированного пред-

ставления – диагональность грамианов управляемости и наблю-

даемости

они определены только для устойчивых си-

стем и представляют собой симметричные матрицы, удовлетво-

ряющие уравнениям Ляпунова:

T T TT

cc oo

+ =- + =-W A AW bb W A A W c c

где А, b, c – матрицы описания в пространстве состояний (приме-

нение этих матриц для анализа управляемости и наблюдаемости

будет описано в разд. 6).

сбалансированное представление обладает рядом полезных

свойств. оно мало чувствительно к погрешностям вычислений и

обеспечивает хорошее качество редукции. Алгоритм построения

126

сбалансированного представления довольно сложен, в пакете

MATLAB он реализуется командой balreal.

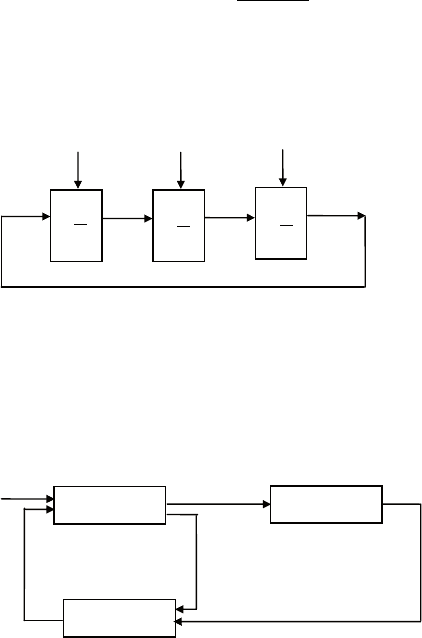
в качестве примера на рис. 4.28 приведена сбалансированная

структурная реализация передаточной функции

() .Qp

характерной чертой этой схемы является ортогональность

сигналов

,,xx

получаемых при

( ).utδ=

это прямое следствие

диагональности грамианов управляемости и наблюдаемости:

15 0

0 0 75

éù

êú

ëû

завершая раздел, посвященный моделированию передаточ-

ных функций, остановимся на их взаимосвязи с другими видами

описания линейных систем – дифференциальными уравнениями,

структурными схемами и описанием в пространстве состояний.

Рис. 4.29. Взаимосвязь описаний линейной системы

Рис. 4.28. Пример сбалансированной реализации







Q







Q





s





s





s



s









 ¨¾É¾½¹ËÇÐÆ¹ØÍÌÆÃÏÁØ

Q2



ÁØ

ÊÇÊËÇØÆÁÂ



ÁÍÍ¾É¾Æ

ÏÁ¹ÄÕÆÔ¾

ÌÉ¹»Æ¾ÆÁØ

ªÎ¾Å¹ÅÇ½¾

ÄÁÉÇ»¹ÆÁØ

§ÈÁÊ¹ÆÁ¾»ÈÉÇ

ÊËÉ¹ÆÊË»¾

ÊÇÊËÇØÆÁÂ

¥¾ËÇ½

£¾ÄÕ»ÁÆ¹

£¹ÆÇÆÁÐ¾ÊÃÁ¾

ÍÇÉÅÔ

ÇÉÅÌÄ¹¥ÖÀÇÆ¹

£¹ÆÇÆÁÐ¾ÊÃÁ¾

ÍÇÉÅÔ

¥¾ËÇ½

£¾ÄÕ»ÁÆ¹

( ) ( )Q p c pE A b

= -

s

127

рис. 4.29 иллюстрирует способы перехода от одного из этих опи-

саний к другим.

Проще всего выглядит взаимосвязь между передаточной

функцией и дифференциальным уравнением – для этого исполь-

зуется прямое и обратное преобразования Лапласа

Пе-

реход от схемы моделирования к передаточной функции может

быть осуществлен с помощью формулы Мэзона, обратный пере-

ход – с помощью одной из канонических форм (фробениусовой,

параллельной, последовательной и т. д.).

описание в пространстве состояний можно получить, исполь-

зуя канонические реализации передаточной функции; для об-

ратного преобразования служит формула

() ( ) .Qp p

=-cEA b

Универсальным средством для построения схемы моделирова-

ния по заданным дифференциальным уравнениям или описанию

в пространстве состояний служит метод кельвина.

все эти виды описания поддерживаются соответствующими

функциями системы MATLAB и SIMULINK.

Задачи и упражнения

1. найти реакцию апериодического звена с передаточной

функцией

()Qp

на входной сигнал

λ-

определить

максимум выходного сигнала при а = 1, λ = 2.

Решение. используя формулу

() ()(),yp Qpup=

получаем

11 11 1

() ,yp

pap apa pλλ λ

æö

=×= -

++ -+ +

èø

откуда

( )

() .

at t

yt e e

Первое слагаемое описывает собственное движение системы,

второе – вынужденную составляющую.

для определения максимума берем производную и приравни-

ваем ее нулю:

()

max

ln ln

,, .

at t a t

ae e e t

λλ

- --

= ==

При а = 1, λ = 2 получим:

2 0 69 0 25

max max

( ) ; ln( ) , ; ( ) , .

yt e e t yt

=- = » =

128

При

aλ =

(особый случай) решение принимает вид:

( ) ; () .

()

y p y t te

При этом t

max

= 1/a, y(t

max

) = 1/ae.

2. Моделируемая система (см. рисунок) представляет собой

кольцо из трех инвертирующих интеграторов, охваченных об-

щей обратной связью.

начальные условия всех

интеграторов одинаковы

и равны 1.

найти характеристи-

ческий полином схемы и

вид выходных сигналов

интеграторов.

Ответ. характеристический полином равен

1,p +

на вы-

ходах интеграторов будут вырабатываться одинаковые затухаю-

щие экспоненты

.()

xt e

3. на рисунке показана структура системы парового отопле-

ния двухэтажного здания.

горячая вода из нагревателя поступает в батареи первого и вто-

рого этажей (резер-

вуары 1 и 2). остыв-

шая вода вновь по-

ступает в резервуар

1. вход u возмеща-

ет возможные рас-

ходы воды.

система описы-

вается дифферен-

циальными уравнениями

1 1 3 212312 3

223 2,, .x xxuxxxxxxx=- + + = - = + -

 

требуется построить схему моделирования и найти весовые

функции от входа u до выходов x

, x

Ответ. весовые функции q

= 1 + 2 e

–3t

; q

= q

= 1 – e

–3t

4. на рисунке приведена структурная схема системы. найти

функции x(t), y(t).

















¦¹¼É¾»¹Ë¾ÄÕ





























©¾À¾É»Ì¹É



©¾À¾É»Ì¹É



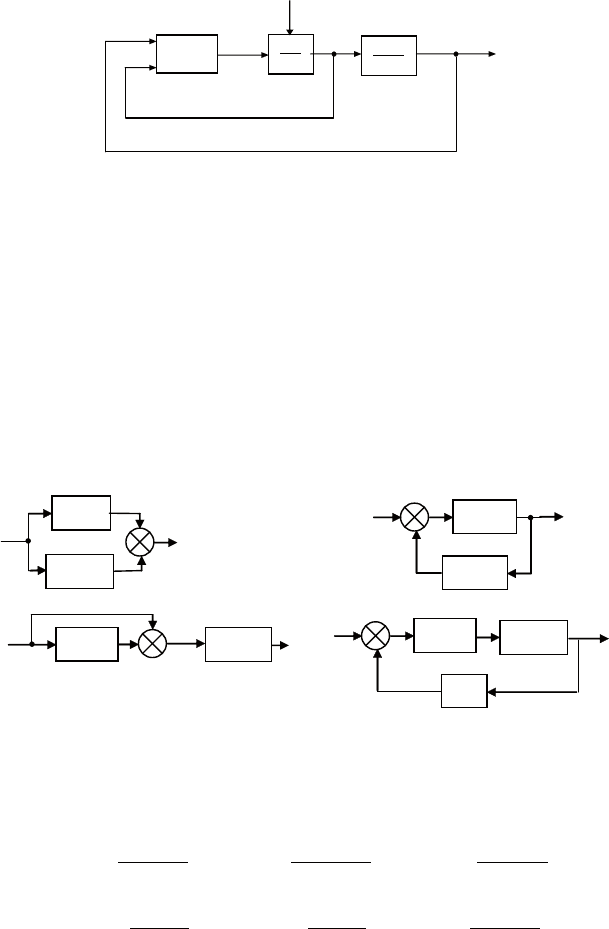
129

s



s





Í

Ë







Решение. По схеме можно записать два операторных уравне-

ния

23 5 1( ); ( ) .px x y p y x- = + - =-

исключаем переменную х:

1 2 3 1 10()(() .p py p y p y- = -+

Получаем характеристическое уравнение

5 40.pp+ +=

его

корни р

= –1, р

= –4.

следовательно,

y Ce Ce

x y y Ce Ce

=-= +



Постоянные С

и С

находим из начальных условий С

= –1,

= 1.

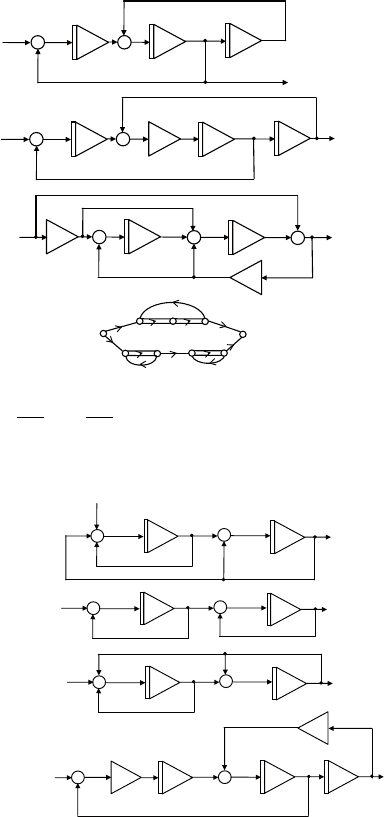
5. на рисунке показаны четыре варианта соединения блоков

( ), ( ).

Qp Wp

Q

V

Z

V

Q

V

Z

s

V

Q

б)

а)

в)

г)

для каждого из них составить схему, пользуясь методом

структурного моделирования и выписать матрицы A, b, c описа-

ния в пространстве состояний.

Передаточные функции блоков

123(), () ( ,,)

Qp Wp i=

име-

ют вид:

12 3

22 2

01 0

() , () , () ,

Qp Qp Qp

pa pap pa

== =

++ +

() , () ,

Wp Wp

pa pa

() .

130

6. используя формулу Мэзона, найти передаточные функции

приведенных ниже схем.

б)

а)

в)

г)



























s

Z

V

s



Ответ. а)

;

б)

;

в) –1; г) 0.

7. используя формулу Мэзона, найти весовые функции при-

веденных ниже схем.



























V







б)

а)

г)

в)

Ответ. a)

; б)

sht

; в) t; г) t

8. Получить две фробениусовы канонические формы для си-

стем с матрицами А вида: