Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.


2.2 Examples of Dynamic Mathematical Models 17
k
1
- constant,
f
1
- cross-sectional area of outflow opening,
g - acceleration gravity.
or
q
1
= k
11
√
h (2.8)
Substituting q
1
from the equation (2.8) into (2.6) yields
dh
dt
=
q
0
F
−
k
11
F
√
h (2.9)
Initial conditions can be arbitrary
h(0) = h
0
(2.10)
The tank will be in a steady-state if
dh
dt
= 0 (2.11)
Let a steady-state be given by a constant flow rate q
s
0
. The liquid height
h
s
then follows from Eq. (2.9) and (2.11) and is given as
h
s
=
(q
s
0
)
2
(k
11
)
2
(2.12)
Interacting Tank-in-Series Process
Consider the interacting tank-in-series process shown in Fig. 2.2. The process
input variable is the flow rate q
0
.
q
0
h
q
1
h
q
2
1
2
Fig. 2.2. An interacting tank-in-series process
The process state variables are heights of liquid in tanks h
1
,h
2
.Mass
balance for the process yields
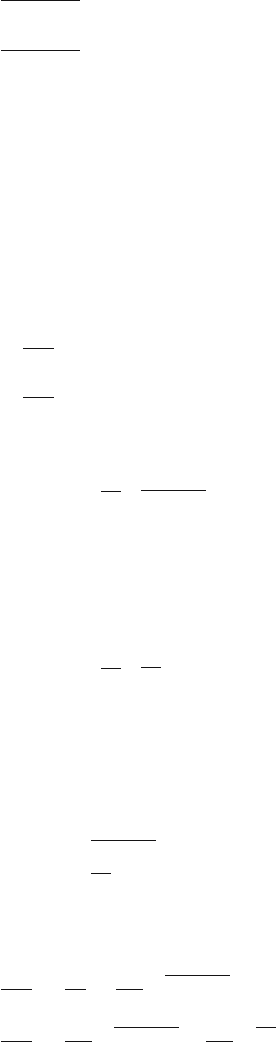
18 2 Mathematical Modelling of Processes
d(F
1
h
1
ρ)
dt
= q
0
ρ −q
1
ρ (2.13)
d(F
2
h
2
ρ)
dt
= q
1
ρ −q
2
ρ (2.14)
where
t - time variable,
h
1
,h
2
- heights of liquid in the first and second tanks,
q
0
- inlet volumetric flow rate to the first tank,
q
1
- inlet volumetric flow rate to the second tank,
q
2
- outlet volumetric flow rate from the second tank,
F
1
,F
2
- cross-sectional area of the tanks,
ρ - liquid density.
Assuming that ρ, F
1
,F
2
are constant we can write
F
1
dh
1
dt
= q
0
− q
1
(2.15)
F
2
dh
2
dt
= q
1
− q
2
(2.16)
Inlet flow rate q
0
is independent of tank states whereas q
1
depends on the
difference between liquid heights
q
1
= k
1
f
1
2g
h
1
− h
2
(2.17)
where
k
1
- constant,
f
1
- cross-sectional area of the first tank outflow opening.
Outlet flow rate q
2
depends on liquid height in the second tank
q
2
= k
2
f
2
2g
h
2
(2.18)
where
k
2
- constant,
f
2
- cross-sectional area of the second tank outflow opening.
Equations (2.17) and (2.18) can then be written as
q
1
= k
11
h
1
− h
2
(2.19)
q
2
= k
22
h
2
(2.20)
Substituting q
1
from Eq. (2.19) and q
2
from (2.20) into (2.15), (2.16) we
get
dh
1
dt
=
q
0
F
1
−
k
11
F
1
h
1
− h
2
(2.21)
dh
2
dt
=
k
11
F
1
h
1
− h
2
−
k
22
F
2
h
2
(2.22)
2.2 Examples of Dynamic Mathematical Models 19
with arbitrary initial conditions
h
1
(0) = h
10
(2.23)
h
2
(0) = h
20
(2.24)
The tanks will be in a steady-state if
dh
1
dt
= 0 (2.25)
dh
2
dt
= 0 (2.26)
Assume a steady-state flow rate q
s
0
. The steady-state liquid levels in both
tanks can be calculated from Eqs (2.21), (2.22), (2.25), (2.26) as
h
s
1
=(q
s
0
)
2
1
(k
11
)
2
+
1
(k
22
)
2
(2.27)
h
s
2
=(q
s
0
)
2
1
(k
22
)
2
(2.28)
2.2.2 Heat Transfer Processes
Heat Exchanger
Consider a heat exchanger for the heating of liquids shown in Fig. 2.3. The
input variables are the temperatures ϑ
v
,ϑ
p
. The state variable is temperature
ϑ.
steam
condensed steam
V
c
q
ϑ
ϑ
ρ
ϑ
p
v
p
q
ϑ
Fig. 2.3. Continuous stirred tank heated by steam in jacket
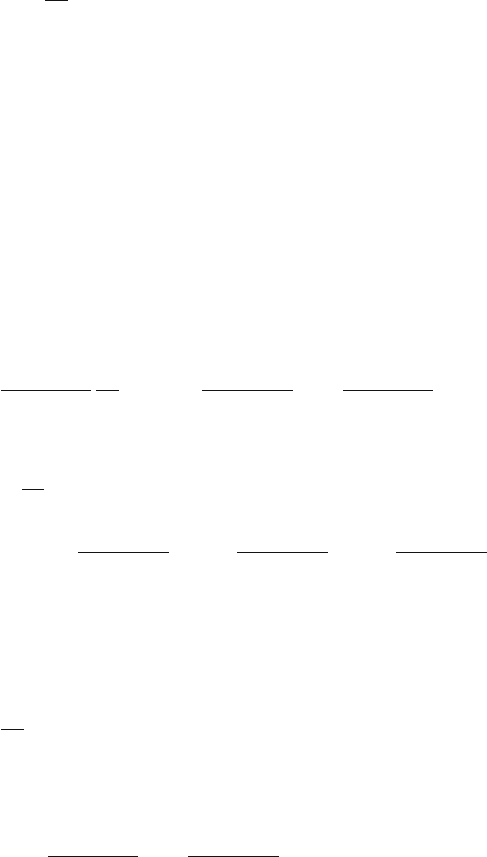
20 2 Mathematical Modelling of Processes
Assume that the wall accumulation ability is small compared to the liquid
accumulation ability and can be neglected. Further assume spatially constant
temperature inside of the tank as the heater is well mixed, constant liquid flow
rate, density, and heat capacity. Then the heat balance equation becomes
Vρc
p
dϑ
dt
= qρc
p
ϑ
v
− qρc
p
ϑ + αF (ϑ
p
− ϑ) (2.29)
where
t - time variable,
ϑ - temperature inside of the exchanger and in the outlet stream,
ϑ
v
- temperature in the inlet stream,
ϑ
p
- jacket temperature,
q - liquid volumetric flow rate,
ρ - liquid density,
V - volume of liquid in the tank,
c
p
- liquid specific heat capacity,
F - heat transfer area of walls,
α - heat transfer coefficient.
Equation (2.29) can be rearranged as
Vρc
p
qρc
p
+ αF
dϑ
dt
= −ϑ +
αF
qρc
p
+ αF
ϑ
p
+
qρc
p
qρc
p
+ αF
ϑ
v
(2.30)
or as
T
1
dϑ
dt
= −ϑ + Z
1
ϑ
p
+ Z
2
ϑ
v
(2.31)
where T
1
=
Vρc
p
qρc
p
+ αF
, Z
1
=
αF
qρc
p
+ αF
, Z
2
=
qρc
p
qρc
p
+ αF
. The initial con-
dition of Eq. (2.30) can be arbitrary
ϑ(0) = ϑ
0
(2.32)
The heat exchanger will be in a steady-state if
dϑ
dt
= 0 (2.33)
Assume steady-state values of the input temperatures ϑ
s
p
,ϑ
s
v
. The steady-
state outlet temperature ϑ
s
can be calculated from Eqs. (2.30), (2.33) as
ϑ
s
=
αF
qρc
p
+ αF
ϑ
s
p
+
qρc
p
qρc
p
+ αF
ϑ
s
v
(2.34)
2.2 Examples of Dynamic Mathematical Models 21
Series of Heat Exchangers
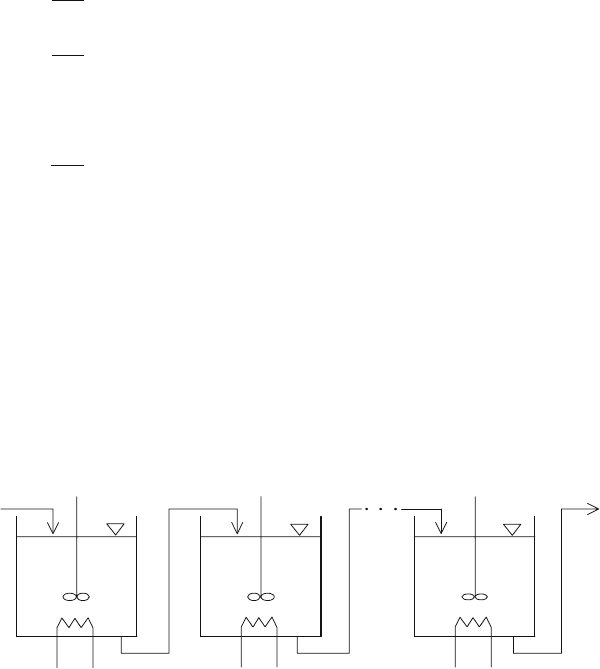
Consider a series of heat exchangers where a liquid is heated (Fig. 2.4). Assume
that heat flows from heat sources into liquid are independent from liquid
temperature. Further assume ideal liquid mixing and zero heat losses. We
neglect accumulation ability of exchangers walls. Hold-ups of exchangers as
well as flow rates, liquid specific heat capacity are constant.
Under these circumstances following heat balances result
V
1
ρc
p
dϑ
1
dt
= qρc
p
ϑ
0
− qρc
p
ϑ
1
+ ω
1
V
2
ρc
p
dϑ
2
dt
= qρc
p
ϑ
1
− qρc
p
ϑ
2
+ ω
2
.
.
.
V
n
ρc
p
dϑ
n
dt
= qρc
p
ϑ
n−1
− qρc
p
ϑ
n
+ ω
n
(2.35)
where
t - time variable,
ϑ
1
,...,ϑ
n
- temperature inside of the heat exchangers,
ϑ
0
- liquid temperature in the first tank inlet stream,
ω
1
,...,ω
n
- heat inputs,
q - liquid volumetric flow rate,
ρ - liquid density,
V
1
,...,V
n
- volumes of liquid in the tanks,
c
p
- liquid specific heat capacity.
1
ϑ
0
ϑ
ω
1
ω
2
1
ϑ
2
ϑ
V
2
V
1
2
ϑ
n-1
ϑ
V
n
n
ϑ
n
ϑ
ω
n
Fig. 2.4. Series of heat exchangers
The process input variables are heat inputs ω
i
and inlet temperature ϑ
0
.
The process state variables are temperatures ϑ
1
,...,ϑ
n
and initial conditions
are arbitrary

22 2 Mathematical Modelling of Processes
ϑ
1
(0) = ϑ
10
,...,ϑ
n
(0) = ϑ
n0
(2.36)
The process will be in a steady-state if
dϑ
1
dt
=
dϑ
2
dt
= ···=
dϑ
n
dt
= 0 (2.37)
Let the steady-state values of the process inputs ω
i
,ϑ
0
be given. The steady-
state temperatures inside the exchangers are
ϑ
s
1
= ϑ
s
0
+
ω
s
1
qρc
p
ϑ
s
2
= ϑ
s
1
+
ω
s
2
qρc
p
.
.
.
ϑ
s
n
= ϑ
s
n−1
+
ω
s
n
qρc
p
(2.38)
Double-Pipe Heat Exchanger
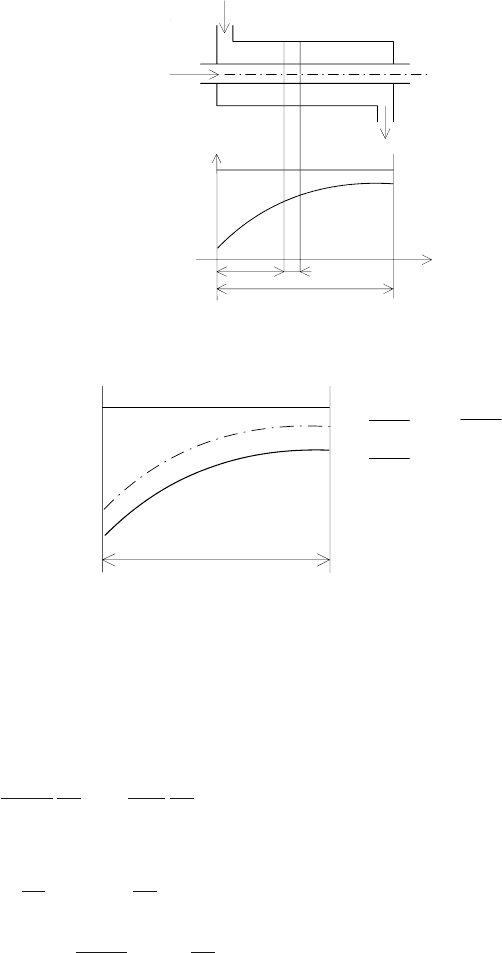
Figure 2.5 represents a single-pass, double-pipe steam-heated exchanger in
which a liquid in the inner tube is heated by condensing steam. The process
input variables are ϑ
p
(t),ϑ(0,t). The process state variable is the temperature
ϑ(σ, t). We assume the steam temperature to be a function only of time, heat
transfer only between inner and outer tube, plug flow of the liquid and zero
heat capacity of the exchanger walls. We neglect heat conduction effects in
the direction of liquid flow. It is further assumed that liquid flow, density, and
specific heat capacity are constant.
Heat balance equation on the element of exchanger length dσ can be de-
rived according to Fig. 2.6
F
σ
dσρc
p
∂ϑ
∂t
= qρc
p
ϑ −qρc
p
ϑ +
∂ϑ
∂σ
dσ
+ αF
d
dσ(ϑ
p
− ϑ) (2.39)
where
t - time variable,
σ - space variable,
ϑ = ϑ(σ, t) - liquid temperature in the inner tube,
ϑ
p
= ϑ
p
(t) - liquid temperature in the outer tube,
q - liquid volumetric flow rate in the inner tube,
ρ - liquid density in the inner tube,
α - heat transfer coefficient,
2.2 Examples of Dynamic Mathematical Models 23
L
δ
δ
v
ϑ
p
s
ϑ
s
d
σ
σ
σ
σ
Fig. 2.5. Double-pipe steam-heated exchanger and temperature profile along the
exchanger length in steady-state
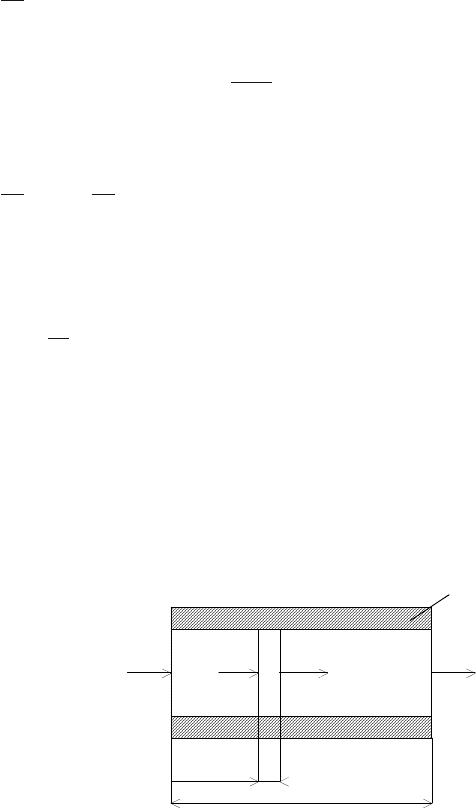
ϑ
p
ϑ
d
σ
+
∂
∂
ϑ
d
t
t
ϑ
+
∂
ϑ
∂σ
d
σ
ϑ
+
∂
ϑ
∂
σ
d
σ
Fig. 2.6. Temperature profile of ϑ in an exchanger element of length dσ for time dt
c
p
- liquid specific heat capacity,
F
d
- area of heat transfer per unit length,
F
σ
- cross-sectional area of the inner tube.
The equation (2.39) can be rearranged to give
F
σ
ρc
p
αF
d
∂ϑ
∂t
= −
qρc
p
αF
d
∂ϑ
∂σ
− ϑ + ϑ
p
(2.40)
or
T
1
∂ϑ
∂t
= −v
σ
T
1
∂ϑ
∂σ
− ϑ + ϑ
p
(2.41)
where T
1
=
F
σ
ρc
p
αF
d
, v
σ
=
q
F
σ
.
Boundary condition of Eq. (2.41) is
ϑ(0,t)=ϑ
0
(t) (2.42)
and initial condition is
24 2 Mathematical Modelling of Processes
ϑ(σ, 0) = ϑ
0
(σ) (2.43)
Assume a steady-state inlet liquid temperature ϑ
0s
and steam temperature
ϑ
s
p
. The temperature profile in the inner tube in the steady-state can be derived
if
∂ϑ
∂t
= 0 (2.44)
as
ϑ
s
(σ)=ϑ
s
p
− (ϑ
s
p
− ϑ
0s
)e
−
σ
v
σ
T
1
(2.45)
If α = 0, Eq. (2.39) reads
∂ϑ
∂t
= −v
σ
∂ϑ
∂σ
(2.46)
while boundary and initial conditions remain the same. If the input variable
is ϑ
0
(t) and the output variable is ϑ(L, t), then Eq. (2.46) describes pure time
delay with value
T
d
=
L
v
σ
(2.47)
Heat Conduction in a Solid Body
Consider a metal rod of length L in Fig. 2.7. Assume ideal insulation of the rod.
Heat is brought in on the left side and withdrawn on the right side. Changes
of densities of heat flows q
0
ω
,q
0
L
influence the rod temperature ϑ(σ, t). Assume
that heat conduction coefficient, density, and specific heat capacity of the rod
are constant. We will derive unsteady heat flow through the rod. Heat balance
on the rod element of length dσ for time dt can be derived from Fig. 2.7 as
Insulation
L
L
q
ω
q
0
ω
q
ω
(σ )
q
ω
σ
d
σ
(σ +
d
σ)
Fig. 2.7. A metal rod

2.2 Examples of Dynamic Mathematical Models 25
F
σ
dσρc
p
∂ϑ
∂t
= F
σ
[q
ω
(σ) −q
ω
(σ + dσ)] (2.48)
or
F
σ
dσρc
p
∂ϑ
∂t
= −F
σ
∂q
ω
∂σ
dσ (2.49)
where
t - time variable,
σ - space variable,
ϑ = ϑ(σ, t) - rod temperature,
ρ - rod density,
c
p
- rod specific heat capacity,
F
σ
- cross-sectional area of the rod,
q
ω
(σ) - heat flow density (heat transfer velocity through unit area) at length
σ,
q
ω
(σ + dσ) - heat flow density at length σ + dσ.
From the Fourier law follows
q
ω
= −λ
∂ϑ
∂σ
(2.50)
where λ is the coefficient of thermal conductivity.
Substituting Eq. (2.50) into (2.49) yields
∂ϑ
∂t
= a
∂
2
ϑ
∂σ
2
(2.51)
where
a =
λ
ρc
p
(2.52)
is the factor of heat conductivity. The equation (2.51) requires boundary and
initial conditions. The boundary conditions can be given with temperatures or
temperature derivatives with respect to σ at the ends of the rod. For example
ϑ(0,t)=ϑ
0
(t) (2.53)
ϑ(L, t)=ϑ
L
(t) (2.54)
The initial condition for Eq. (2.51) is
ϑ(σ, 0) = ϑ
0
(σ) (2.55)
Consider the boundary conditions (2.53), (2.54). The process input variables
are ϑ
0
(t),ϑ
L
(t) and the state variable is ϑ(σ, t).
Assume steady-state temperatures ϑ
0s
,ϑ
Ls
. The temperature profile of the
rod in the steady-state can be derived if

26 2 Mathematical Modelling of Processes
∂ϑ
∂t
= 0 (2.56)
as
ϑ
s
(σ)=ϑ
0s
+
ϑ
Ls
− ϑ
0s
L
σ (2.57)
2.2.3 Mass Transfer Processes
Packed Absorption Column
A scheme of packed countercurrent absorption column is shown in Fig. 2.8
where
t - time variable,
σ - space variable,
L - height of column,
G - molar flow of gas phase,
c
y
= c
y
(σ, t) - molar fraction concentration of a transferable component in
gas phase,
Q - molar flow of liquid phase,
c
x
= c
x
(σ, t) - molar fraction concentration of a transferable component in
liquid phase.
GQ
G
Q
L
σ
c
y
c
x
d
σ
Fig. 2.8. A scheme of a packed countercurrent absorption column
Absorption represents a process of absorbing components of gaseous sys-
tems in liquids.
We assume ideal filling, plug flow of gas and liquid phases, negligible mixing
and mass transfer in phase flow direction, uniform concentration profiles in
both phases at cross surfaces, linear equilibrium curve, isothermal conditions,
constant mass transfer coefficients, and constant flow rates G, Q.
Considering only the process state variables c
x
,c
y
and the above given
simplifications and if only the physical process of absorption is considered then
