Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.

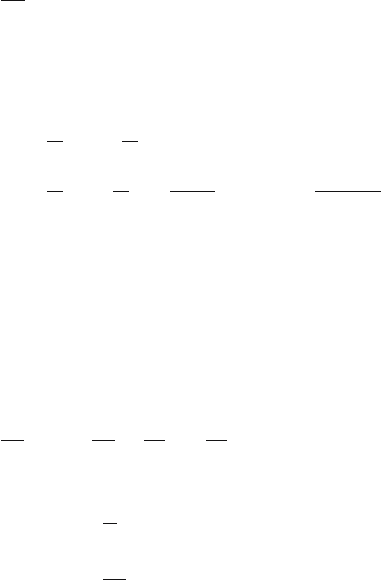
2.3 General Process Models 37
x
1
= c
A
x
2
= ϑ
u
1
= ϑ
c
r
1
= c
Av
r
2
= ϑ
v
and assuming that temperature measurement of ϑ is available, state and
output equations are given as
dx
dt
= f(x, u, r)
y
1
=(01)x
where
x =
x
1
x
2
, u = u
1
, r =
r
1
r
2
, f =
f
1
f
2
f
1
=
q
V
c
Av
−
q
V
c
A
− r(c
A
,ϑ)
f
2
=
q
V
ϑ
v
−
q
V
ϑ +
αF
Vρc
p
(ϑ −ϑ
c
)+
(−ΔH)
ρc
p
r(c
A
,ϑ)
Example 2.3: Double-pipe steam-heated exchanger - state equations
Processes with distributed parameters are usually approximated by a se-
ries of well-mixed lumped parameter processes. This is also the case for
the heat exchanger shown in Fig. 2.5 which is divided into n well-mixed
heat exchangers. The space variable is divided into n equal lengths within
the interval [0,L]. However, this division can also be realised differently.
Mathematical model of the exchanger is of the form
∂ϑ
∂t
= −v
σ
∂ϑ
∂σ
−
1
T
1
ϑ +
1
T
1
ϑ
p
Introduce
x
1
(t)=ϑ
L
n
,t
x
2
(t)=ϑ
2L
n
,t
.
.
.
x
n
(t)=ϑ(L, t)
u
1
(t)=ϑ
p
(t)
r
1
(t)=ϑ(0,t)
and replace ∂ϑ/∂σ with the corresponding difference. The resulting model
consits of a set of ordinary differential equations
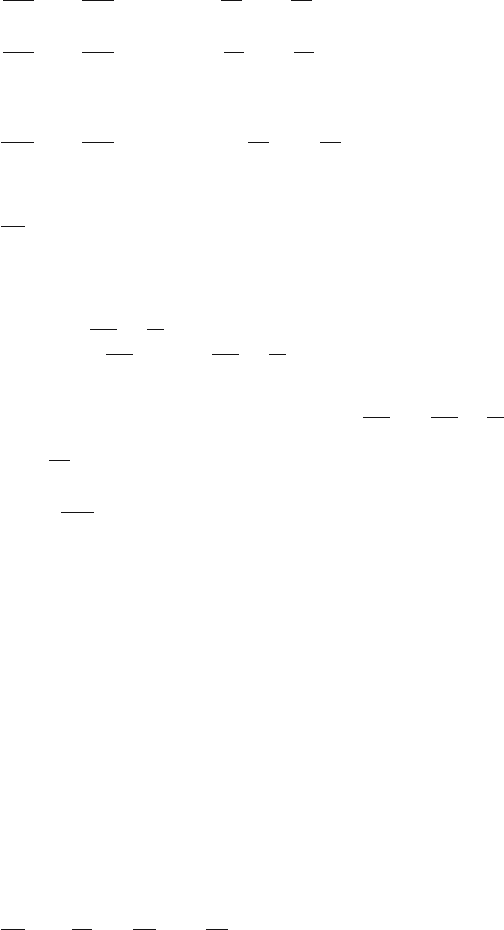
38 2 Mathematical Modelling of Processes
dx
1
dt
= −
v
σ
n
L
(x
1
− r
1
) −
1
T
1
x
1
+
1
T
1
u
1
dx
2
dt
= −
v
σ
n
L
(x
2
− x
1
) −
1
T
1
x
2
+
1
T
1
u
1
.
.
.
dx
n
dt
= −
v
σ
n
L
(x
n
− x
n−1
) −
1
T
1
x
n
+
1
T
1
u
1
The state equation is given as
dx
dt
= Ax + Bu
1
+ Hr
1
where
x =(x
1
... x
n
)
T
A =
⎛
⎜
⎜
⎜
⎝
−(
v
σ
n
L
+
1
T
1
)00... 00
v
σ
n
L
−(
v
σ
n
L
+
1
T
1
)0... 00
.
.
.
.
.
.
.
.
. ...
.
.
.
.
.
.
000...
v
σ
n
L
−(
v
σ
n
L
+
1
T
1
)
⎞
⎟
⎟
⎟
⎠
B =
1
T
1
(1 ... 1)
T
H =
v
σ
n
L
0 ... 0
T
Assume that temperature is measured at σ
1
=2L/n and/or σ
2
= L. Then
the output equation is of the form
y = Cx
where
y =
y
1
y
2
, C =
010 ... 0
000 ... 1
or
y
1
= Cx, C =(000 ... 1)
Example 2.4: Heat exchanger - dimensionless variables
The state equation for the heat exchanger shown in Fig. 2.3 is
dϑ
dt
= −
1
T
1
ϑ +
Z
1
T
1
ϑ
p
+
Z
2
T
1
ϑ
v
where t
is time variable. The exchanger is in a steady-state if dϑ/dt
=0.
Denote steady-state temperatures ϑ
s
p
,ϑ
s
v
,ϑ
s
. For the steady-state yields
ϑ
s
= Z
1
ϑ
s
p
+ Z
2
ϑ
s
v

2.4 Linearisation 39
Define dimensionless variables
x
1
=
ϑ
ϑ
s
u
1
=
ϑ
p
ϑ
s
p
r
1
=
ϑ
v
ϑ
s
v
t =
t
T
1
then the state equation is given as
dx
1
dt
= −x
1
+
Z
1
ϑ
s
p
ϑ
s
u
1
+
Z
2
ϑ
s
v
ϑ
s
r
1
with initial condition
x
1
(0) = x
10
=
ϑ(0)
ϑ
s
2.4 Linearisation
Linearisation of nonlinear models plays an important role in practical con-
trol design. The principle of linearisation of nonlinear equations consists in
supposition that process variables change very little and their deviations from
steady-state remain small. Linear approximation can be obtained by using the
Taylor series expansion and considering only linear terms. This approxima-
tion is then called linearised model. An advantage of linear models is their
simplicity and their use can yield to analytical results.
Let us recall the Taylor theorem:Leta, x be different numbers, k ≥ 0and
J is a closed interval with endpoints a, x.Letf be a function with continuous
k-th derivative on J and k + 1-th derivative within this interval. Then there
exists a point ζ within J such that
f(x)=f(a)+
˙
f(a)
1!
(x −a)+
¨
f(a)
2!
(x −a)
2
+ ···+
f
(k)
(a)
k!
(x −a)
k
+ R
k
(x)
(2.114)
where R
k
(x)=
f
(k+1)
(ζ)
(k+1)!
(x −a)
k+1
is the rest of the function f after the k-th
term of the Taylor’s polynomial.
Consider a process described by a set of equations
dx
i
dt
= f
i
(x
, u
)=f
i
(x
1
,...,x
n
,u
1
,...,u
m
),i=1,...,n (2.115)
where
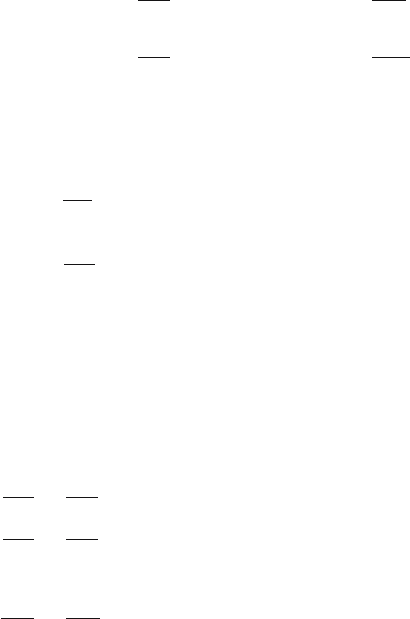
40 2 Mathematical Modelling of Processes
x
- vector of state variables x
1
,...,x
n
,
u
- vector of manipulated variables u
1
,...,u
m
.
Let the process state variables x
i
change in the neighbourhood of the
steady-state x
s
i
under the influence of the manipulated variables u
i
. Then it
is possible to approximate the process nonlinearities. The steady-state is given
by the equation
0=f
i
(x
s
, u
s
)=f
s
i
(2.116)
We suppose that the solution of these equations is known for some u
s
j
,j =
1,...,m. The function f
i
(•) is approximated by the Taylor series expansion
truncated to only first order terms as
f
i
(x
, u
)
.
= f
i
(x
s
, u
s
)+
+
∂f
i
∂x
1
s
(x
1
− x
s
1
)+···+
∂f
i
∂x
n
s
(x
n
− x
s
n
)+
+
∂f
i
∂u
1
s
(u
1
− u
s
1
)+···+
∂f
i
∂u
m
s
(u
m
− u
s
m
) (2.117)
(∂f
i
/∂x
l
)
s
, l =1,...,n and
∂f
i
/∂u
j
s
, j =1,...,m denote partial deriva-
tives for x
l
= x
s
l
and u
j
= u
s
j
, respectively. Therefore, these partial deriva-
tives are constants
a
il
=
∂f
i
∂x
l
s
l =1,...,n (2.118)
b
ij
=
∂f
i
∂u
j
s
j =1,...,m (2.119)
From Eq. (2.116) follows that the first term on the right side of (2.117) is
zero. Introducing state and manipulated deviation variables
x
i
= x
i
− x
s
i
(2.120)
u
j
= u
j
− u
s
j
(2.121)
gives
dx
1
dt
=
dx
1
dt
= a
11
x
1
+ ···+ a
1n
x
n
+ b
11
u
1
+ ···+ b
1m
u
m
dx
2
dt
=
dx
2
dt
= a
21
x
1
+ ···+ a
2n
x
n
+ b
21
u
1
+ ···+ b
2m
u
m
.
.
.
dx
n
dt
=
dx
n
dt
= a
n1
x
1
+ ···+ a
nn
x
n
+ b
n1
u
1
+ ···+ b
nm
u
m
(2.122)
We denote x the vector of deviation state variables and u the vector of devi-
ation manipulated variables. Then (2.122) can be written as

2.4 Linearisation 41
dx
dt
= Ax + Bu (2.123)
where
A =
⎛
⎜
⎜
⎜
⎝
a
11
a
12
... a
1n
a
21
a
22
... a
2n
.
.
.
.
.
. ...
.
.
.
a
n1
a
n2
... a
nn
⎞
⎟
⎟
⎟
⎠
B =
⎛
⎜
⎜
⎜
⎝
b
11
b
12
... b
1m
b
21
b
22
... b
2m
.
.
.
.
.
. ...
.
.
.
b
n1
b
n2
... b
nm
⎞
⎟
⎟
⎟
⎠
Equation (2.123) is a linearised differential equation. If initial state of (2.115)
also represent steady-state of the modelled process then
x(0) = 0 (2.124)
Equations (2.115), (2.123) describe dynamics of a process. The differences
are as follows:
1. equation (2.123) is only an approximation,
2. equation (2.123) uses deviation variables,
3. equation (2.123) is linear with constant coefficients.
Linearisation of the process dynamics must be completed with linearisation
of the output equation if this is nonlinear.
Consider the output equation of the form
y
k
= g
k
(x
, u
),k=1,...,r (2.125)
where y
k
are the output variables. In the steady-state holds
y
s
k
= g
k
(x
s
, u
s
) (2.126)
Introducing output deviation variables
y
k
= y
k
− y
s
k
(2.127)
follows
y
k
= g
k
(x
s
+ x, u
s
+ u) − g
k
(x
s
, u
s
) (2.128)
Using the Taylor series expansion with only linear terms the following approx-
imation holds
g
k
(x
, u
)
.
= g
k
(x
s
, u
s
)+
n
l=1
∂g
k
∂x
l
s
(x
l
− x
s
l
)
+
m
j=1
∂g
k
∂u
j
s
(u
j
− u
s
j
) (2.129)

42 2 Mathematical Modelling of Processes
and again the partial derivatives in (2.129) are constants
c
kl
=
∂g
k
∂x
l
s
l =1,...,n (2.130)
d
kj
=
∂g
k
∂u
j
s
j =1,...,m (2.131)
Output deviation variables are then of the form
y
1
= c
11
x
1
+ ···+ c
1n
x
n
+ d
11
u
1
+ ···+ d
1m
u
m
y
2
= c
21
x
1
+ ···+ c
2n
x
n
+ d
21
u
1
+ ···+ d
2m
u
m
.
.
.
y
r
= c
r1
x
1
+ ···+ c
rn
x
n
+ d
r1
u
1
+ ···+ d
rm
u
m
(2.132)
If y denotes the vector of output deviation variables then the previous equation
can more compactly be written as
y = Cx + Du (2.133)
where
C =
⎛
⎜
⎜
⎜
⎝
c
11
c
12
... c
1n
c
21
c
22
... c
2n
.
.
.
.
.
. ...
.
.
.
c
r1
c
r2
... c
rn
⎞
⎟
⎟
⎟
⎠
D =
⎛
⎜
⎜
⎜
⎝
d
11
d
12
... d
1m
d
21
d
22
... d
2m
.
.
.
.
.
. ...
.
.
.
d
r1
d
r2
... d
rm
⎞
⎟
⎟
⎟
⎠
Equations (2.123) and (2.133) constitute together the general linear state
process model. When it is obtained from the linearisation procedure, then it
can only be used in the neighbourhood of the steady-state where linearisation
was derived.
Example 2.5: Liquid storage tank - linearisation
Consider the liquid storage tank shown in Fig. 2.1. The state equation of
this process is
dh
dt
= f
1
(h, q
0
)
where
f
1
(h, q
0
)=−
k
11
F
√
h +
1
F
q
0
The steady-state equation is
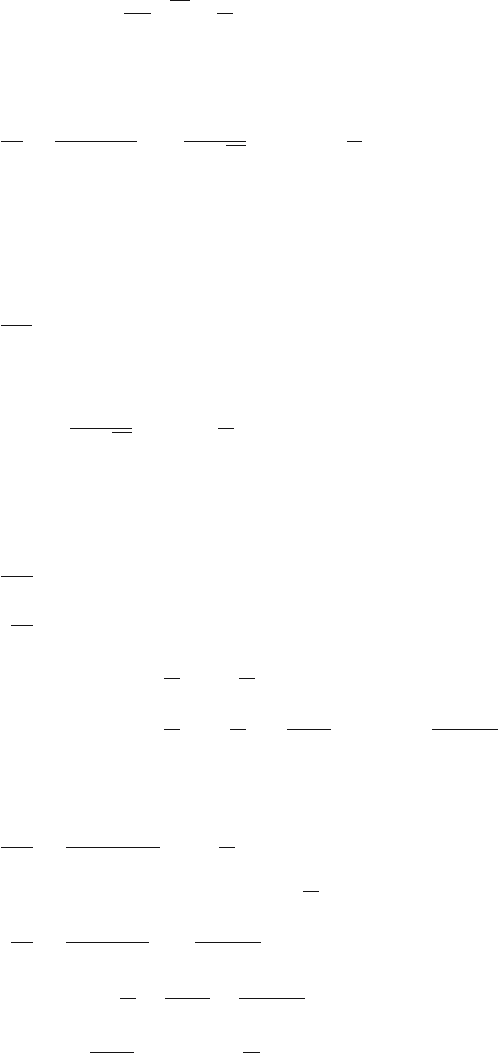
2.4 Linearisation 43
f
1
(h
s
,q
s
0
)=−
k
11
F
√
h
s
+
1
F
q
s
0
=0
Linearised state equation for a neighbourhood of the steady-state given
by q
s
0
,h
s
can be written as
dh
dt
=
d(h −h
s
)
dt
= −
k
11
2F
√
h
s
(h −h
s
)+
1
F
(q
0
− q
s
0
)
Introducing deviation variables
x
1
= h − h
s
u
1
= q
0
− q
s
0
and assuming that the level h is measured then the linearised model of
the tank is of the form
dx
1
dt
= a
11
x
1
+ b
11
u
1
y
1
= x
1
where
a
11
= −
k
11
2F
√
h
s
,b
11
=
1
F
Example 2.6: CSTR - linearisation
Consider the CSTR shown in Fig. 2.11. The state equations for this reactor
are
dc
A
dt
= f
1
(c
A
,c
Av
,ϑ)
dϑ
dt
= f
2
(c
A
,ϑ,ϑ
v
,ϑ
c
)
where
f
1
(c
A
,c
Av
,ϑ)=
q
V
c
Av
−
q
V
c
A
− r(c
A
,ϑ)
f
2
(c
A
,ϑ,ϑ
v
,ϑ
c
)=
q
V
ϑ
v
−
q
V
ϑ −
αF
Vρc
p
(ϑ −ϑ
c
)+
(−ΔH)
ρc
p
r(c
A
,ϑ)
Linearised dynamics equations for the neighbourhood of the steady-state
given by steady-state input variables ϑ
s
c
,c
s
Av
,ϑ
s
v
and steady-state process
state variables c
s
A
,ϑ
s
are of the form
dc
A
dt
=
d(c
A
− c
s
A
)
dt
=
−
q
V
− ˙r
c
A
(c
s
A
,ϑ
s
)
(c
A
− c
s
A
)
+(−˙r
ϑ
(c
s
A
,ϑ
s
))(ϑ −ϑ
s
)+
q
V
(c
Av
− c
s
Av
)
dϑ
dt
=
d(ϑ −ϑ
s
)
dt
=
(−ΔH)
ρc
p
˙r
c
A
(c
s
A
,ϑ
s
)
(c
A
− c
s
A
)
+
−
q
V
−
αF
Vρc
p
+
(−ΔH)
ρc
p
˙r
ϑ
(c
s
A
,ϑ
s
)
(ϑ −ϑ
s
)
+
αF
Vρc
p
(ϑ
c
− ϑ
s
c
)+
q
V
(ϑ
v
− ϑ
s
v
)
44 2 Mathematical Modelling of Processes
where
˙r
c
A
(c
s
A
,ϑ
s
)=
∂r(c
A
,ϑ)
∂c
A
c
A
= c
s
A
ϑ = ϑ
s
˙r
ϑ
(c
s
A
,ϑ
s
)=
∂r(c
A
,ϑ)
∂ϑ
c
A
= c
s
A
ϑ = ϑ
s
Introducing deviation variables
x
1
= c
A
− c
s
A
x
2
= ϑ − ϑ
s
u
1
= ϑ
c
− ϑ
s
c
r
1
= c
Av
− c
s
Av
r
2
= ϑ
v
− ϑ
s
v
and considering temperature measurements of ϑ then for the linearised
process model follows
dx
1
dt
= a
11
x
1
+ a
12
x
2
+ h
11
r
1
dx
2
dt
= a
21
x
1
+ a
22
x
2
+ b
21
u
1
+ h
22
r
2
y
1
= x
2
where
a
11
= −
q
V
− ˙r
c
A
(c
s
A
,ϑ
s
),a
12
= −˙r
ϑ
(c
s
A
,ϑ
s
)
a
21
=
(−ΔH)
ρc
p
˙r
c
A
(c
s
A
,ϑ
s
),a
22
= −
q
V
−
αF
Vρc
p
+
(−ΔH)
ρc
p
˙r
ϑ
(c
s
A
,ϑ
s
))
b
21
=
αF
Vρc
p
h
11
= h
22
=
q
V
If the rate of reaction is given as (the first order reaction)
r(c
A
,ϑ)=c
A
k
0
e
−
E
Rϑ
then
˙r
c
A
(c
s
A
,ϑ
s
)=k
0
e
−
E
Rϑ
s
˙r
ϑ
(c
s
A
,ϑ
s
)=c
s
A
k
0
E
R(ϑ
s
)
2
e
−
E
Rϑ
s
The deviation variables have the same meaning as before: x
1
,x
2
are state
deviation variables, u
1
is a manipulated deviation variable, and r
1
,r
2
are
disturbance deviation variables.
2.5 Systems, Classification of Systems 45
2.5 Systems, Classification of Systems
A deterministic single-input single-output (SISO) system is a physical device
which has only one input u(t) and the result of this influence is an observable
output variable y(t). The same initial conditions and the same function u(t)
lead to the same output function y(t). This definition is easily extended to
deterministic multi-input multi-output (MIMO) systems whose input variables
are u
1
(t),...,u
m
(t) and output variables are y
1
(t),...,y
r
(t). The concept of
asystemis based on the relation between cause and consequence of input and
output variables.
Continuous-time (CT) systems are systems with all variables defined for
all time values.
Lumped parameter systems have influence between an input and output
variables given by ordinary differential equations with derivatives with respect
to time. Systems with distributed parameters are described by partial differ-
ential equations with derivatives with respect to time and space variables.
If the relation between an input and output variable for deterministic CT
SISO system is given by ordinary differential equations with order greater than
one, then it is necessary for determination of y(t),t > t
0
to know u(t),t >
t
0
and output variable y(t
0
) with its derivatives at t
0
or some equivalent
information. The necessity of knowledge about derivatives avoids introduction
of concept of state.
Linear systems obey the law of superposition.
The systems described in Section 2.2 are examples of physical systems.
The systems determined only by variables that define a relation between the
system elements or between the system and its environment are called abstract.
Every physical system has a corresponding abstract model but not vice versa.
A notation of oriented systems can be introduced. This is every controlled
system with declared input and output variables.
The relation between objects (processes) and systems can be explained
as follows. If a process has defined some set of typical important properties
significant for our investigations then we have defined a system on the process.
We note that we will not further pursue special details and differences
between systems and mathematical relations describing their behaviour as it
is not important for our purposes.
Analogously as continuous-time systems were defined, discrete-time (DT)
systems have their variables defined only in certain time instants.
The process model examples were chosen to explain the procedure for sim-
plification of models. Usually, two basic steps were performed. Models given
by partial differential equations were transformed into ordinary differential
equations and nonlinear models were linearised. Step-wise simplifications of
process models led to models with linear differential equations. As computer
control design is based on DT signals, the last transformation is toward DT
systems.
46 2 Mathematical Modelling of Processes
A Stochastic system is characterised by variables known only with some
probability.
Therefore, classification of dynamical systems can be clearly given as in
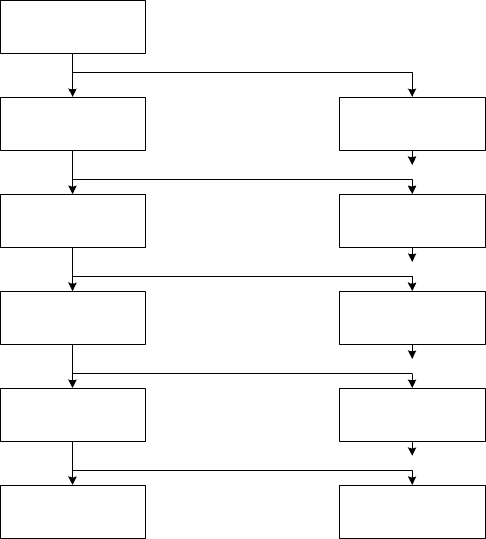
Fig. 2.12.
Dynamical
systems
lumped
parameters
distributed
parameters
deterministic stochastic
linear nonlinear
with constant
coefficients
with variable
coefficients
discrete continuous
Fig. 2.12. Classification of dynamical systems
2.6 References
Mathematical models of processes are discussed in more detail in works:
J.
ˇ
Cerm´ak, V. Peterka, and J. Z´avorka. Dynamics of Controlled Systems in
Thermal Energetics and Chemistry. Academia, Praha, 1968. (in Czech).
C. J. Friedly. Dynamic Behavior of Processes. Prentice Hall, Inc., New Jersey,
1972.
L. N. Lipatov. Typical Processes of Chemical Technology as Objects for Con-
trol. Chimija, Moskva, 1973. (in Russian).
