Mikles J., Fikar M. Process Modelling, Identification, and Control
Подождите немного. Документ загружается.

2.7 Exercises 47
V. V. Kafarov, V. L Perov, and B. P. Meˇsalkin. Principles of Mathematical
Modelling of Systems in Chemical Technology. Chimija, Moskva, 1974. (in
Russian).
G. Stephanopoulos. Chemical Process Control, An Introduction to Theory and
Practice. Prentice Hall, Englewood Cliffs, New Jersey, 1984.
D. Chm´urny, J. Mikleˇs, P. Dost´al, and J. Dvoran. Modelling and Control of
Processes and Systems in Chemical Technology. Alfa, Bratislava, 1985.
(in Slovak).
W. L. Luyben. Process Modelling, Simulation and Control for Chemical En-
gineers. McGraw Hill, Singapore, 2 edition, 1990.
B. Wittenmark, J. K.
˚
Astr
¨
om, and S. B. Jørgensen. Process Control. Lund
Institute of Technology, Technical University of Denmark, Lyngby, 1992.
J. Ingham, I. J. Dunn, E. Henzle, and J. E. Pˇrenosil. Chemical Engineering
Dynamics. VCH Verlagsgesselschaft, Weinheim, 1994.
Mathematical models of unit processes are also given in many journal
articles. Some of them are cited in books above. These are completed by
articles dealing with bioprocesses:
J. Bhat, M. Chidambaram, and K. P. Madhavan. Robust control of a batch-fed
fermentor. Journal of Process Control, 1:146 – 151, 1991.
B. Dahhou, M. Lakrori, I. Queinnec, E. Ferret, and A. Cherny. Control of
continuous fermentation process. Journal of Process Control, 2:103 – 111,
1992.
M. Rauseier, P. Agrawal, and D. A. Melichamp. Non-linear adaptive control
of fermentation processes utilizing a priori modelling knowledge. Journal
of Process Control, 2:129 – 138, 1992.
Some works concerning definitions and properties of systems:
L. A. Zadeh and C. A. Desoer. Linear System Theory - the State-space Ap-
proach. McGraw-Hill, New York, 1963.
E. D. Gilles. Systeme mit verteilten Parametern, Einf
¨
uhrung in die Regelungs-
theorie. Oldenbourg Verlag, M
¨
unchen, 1973.
V. Strejc. State-space Theory of Linear Control. Academia, Praha, 1978. (in
Czech).
A. A. Voronov. Stability, Controllability, Observability. Nauka, Moskva, 1979.
(in Russian).
2.7 Exercises
Exercise 2.1:
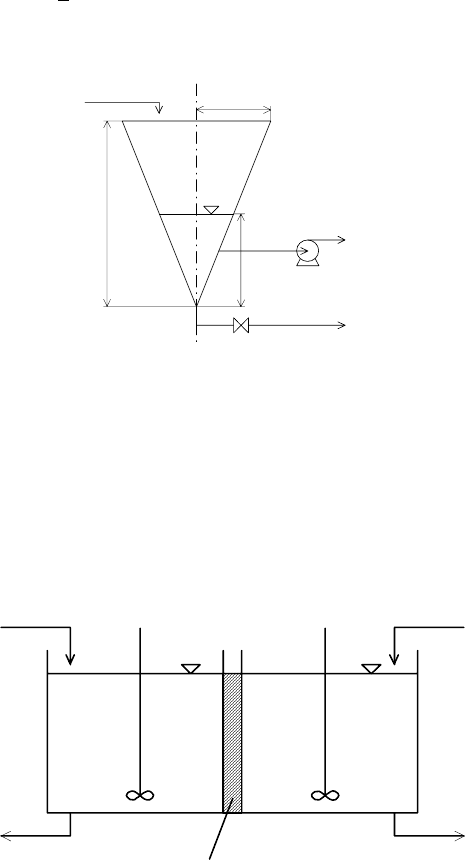
Consider the liquid storage tank shown in Fig. 2.13. Assume constant liquid
density and constant flow rate q
1
. Flow rate q
2
can be expressed as
48 2 Mathematical Modelling of Processes
q
2
= k
10
h + k
11
√
h
2
q
max
h
h
r
0
q
1
q
Fig. 2.13. A cone liquid storage process
Find:
1. state equation,
2. linearised process model.
Exercise 2.2:
A double vessel is used as a heat exchanger between two liquids separated by
a wall (Fig. 2.14).
1
ϑ
2
ϑ
1v
ϑ
2v
ϑ
1
α
2
α
c
p1
c
p2
q
1
q
2
1
ρ
2
ρ
V
1
V
2
V
ww
ϑ
w
ρ
c
pw
1
ϑ
q
1
2
ϑ
q
2
Fig. 2.14. Well mixed heat exchanger
Assume heating of a liquid with a constant volume V
2
with a liquid with a
constant volume V
1
. Heat transfer is considered only in direction vertical to
the wall with temperature ϑ
w
(t), volume V
w
, density ρ
w
, and specific heat
2.7 Exercises 49
capacity c
pw
. Heat transfer from the process toits environment is neglected.
Further, assume spatially constant temperatures ϑ
1
and ϑ
2
, constant densities
ρ
1
,ρ
2
, flow rates q
1
,q
2
, specific heat capacities c
p1
,c
p2
. α
1
is the heat transfer
coefficient from liquid to wall and α
2
is the heat transfer coefficient from
wall to liquid. The process state variables are ϑ
1
,ϑ
2
,ϑ
w
. The process input
variables are ϑ
1v
,ϑ
2v
.
1. Find state equations,
2. introduce dimensionless variables and rewrite the state equations.
Exercise 2.3:
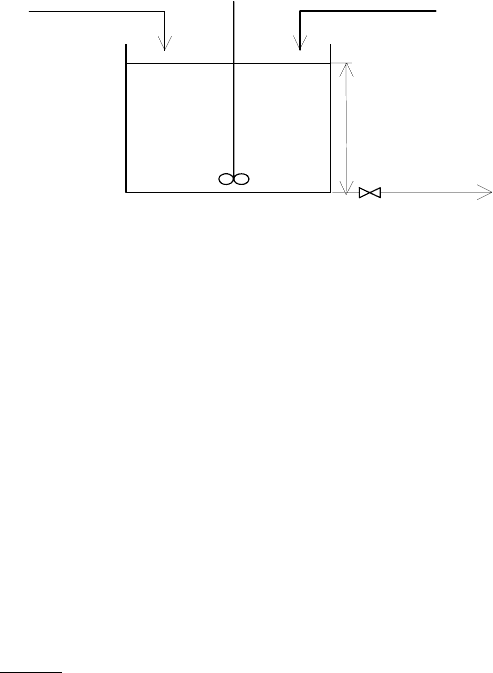
A tank is used for blending of liquids (Fig. 2.15). The tank is filled up with
two pipelines with flow rates q
1
,q
2
. Both streams contain a component with
constant concentrations c
0
,c
1
. The outlet stream has a flow rate q
2
and con-
centration c
2
. Assume that the concentration within tank is c
2
.
F
qc
0
0
qc
1
1
qc
2
2
c
2
1
h
Fig. 2.15. A well mixed tank
Find:
1. state equations,
2. linearised process model.
Exercise 2.4:
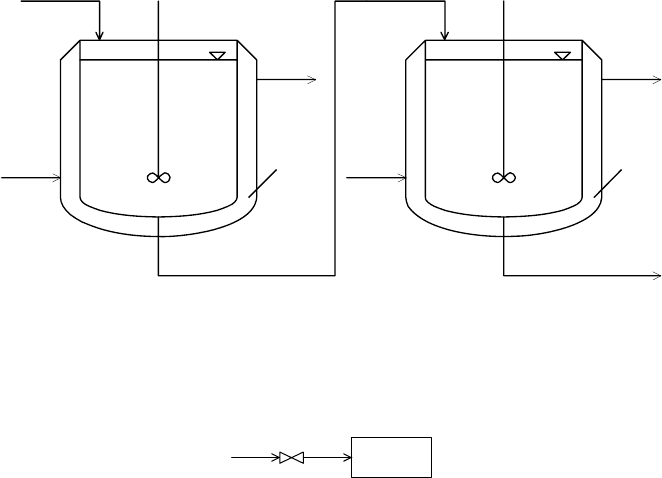
An irreversible reaction A → B occurs in a series of CSTRs shown in Fig. 2.16.
The assumptions are the same as for the reactor shown in Fig. 2.11.
1. Find state equations,
2. construct linearised process model.
Exercise 2.5:
Consider the gas tank shown in Fig. 2.17. A gas with pressure p
0
(t)flows
through pneumatic resistance (capillary) R
1
to the tank with volume V .The
pressure in the tank is p
1
(t). Molar flow rate G of the gas through resistance
R
1
is
G =
p
0
− p
1
R
1
50 2 Mathematical Modelling of Processes
Av
c
v
ϑ
1
ϑ
c1
ϑ
V
1
1
ϑ
V
2
2
ϑ
c2
ϑ
2
ϑ
A2
c
A2
c
A1
c
A1
c
Fig. 2.16. Series of two CSTRs
Assume that the ideal gas law holds. Find state equation of the tank.
V
p
1
p
0
Fig. 2.17. A gas storage tank

3
Analysis of Process Models
Mathematical models describing behaviour of a large group of technological
processes can under some simplifications be given by linear differential equa-
tions with constant coefficients. Similarly, other blocks of control loops can
also be described by linear differential equations with constant coefficients.
For investigation of the dynamical properties of processes it is necessary to
solve differential equations with time as independent variable. Linear differen-
tial equations with constant coefficients can be very suitably solved with the
help of the Laplace transform.
Analysis of dynamical systems is based on their state-space representation.
The spate-space representation is closely tied to input-output representation
of the systems that are described by input-output process models. In this
chapter we will define the Laplace transform and show how to solve by means
of it linear differential equations with constant coefficients. We introduce the
definition of transfer function and transfer function matrix. Next, the concept
of states and connection between state-space and input-output models will be
given. We examine the problem of stability, controllability, and observability
of continuous-time processes.
3.1 The Laplace Transform
The Laplace transform offers a very simple and elegant vehicle for the solution
of differential equations with constant coefficients. It further enables to derive
input-output models which are suitable for process identification and control.
Moreover, it simplifies the qualitative analysis of process responses subject to
various input signals.
3.1.1 Definition of the Laplace Transform
Consider a function f(t). The Laplace transform is defined as
52 3 Analysis of Process Models
L{f(t)} =
∞
0
f(t)e
−st
dt (3.1)
where L is an operator defined by the integral, f(t) is some function of time.
The Laplace transform is often written as
F (s)=L{f(t)} (3.2)
The function f (t) given over an interval 0 ≤ t<∞ is called the time original
and the function F (s) its Laplace transform. The function f(t) must satisfy
some conditions. It must be piecewise continuous for all times from t =0to
t = ∞. This requirement practically always holds for functions used in mod-
elling and control. It follows from the definition integral that we transform
the function from the time domain into s domain where s is a complex vari-
able. Further it is clear that the Laplace transform of a function exists if the
definition integral is bounded. This condition is fulfilled for all functions we
will deal with.
The function F (s) contains no information about f(t)fort<0. This is
no real obstacle as t is the time variable usually defined as positive. Variables
and systems are then usually defined such that
f(t) ≡ 0fort<0 (3.3)
If the equation (3.3) is valid for the function f(t), then this is uniquely given
except at the points of incontinuities with the L transform
f(t)=L
−1
{F (s)} (3.4)
This equation defines the inverse Laplace transform.
The Laplace transform is a linear operator and satisfies the principle of
superposition
L{k
1
f
1
(t)+k
2
f
2
(t)} = k
1
L{f
1
(t)} + k
2
L{f
2
(t)} (3.5)
where k
1
,k
2
are some constants. The proof follows from the definition integral
L{k
1
f
1
(t)+k
2
f
2
(t)} =
∞
0
[k
1
f
1
(t)+k
2
f
2
(t)]e
−st
dt
= k
1
∞
0
f
1
(t)e
−st
dt + k
2
∞
0
f
2
(t)e
−st
dt
= k
1
L{f
1
(t)} + k
2
L{f
2
(t)}
An important advantage of the Laplace transform stems from the fact
that operations of derivation and integration are transformed into algebraic
operations.

3.1 The Laplace Transform 53
3.1.2 Laplace Transforms of Common Functions
Step Function
The Laplace transform of step function is very important as step functions
and unit step functions are often used to investigate the process dynamical
properties and in control applications.
6
?
tt =0
f(t)
A
Fig. 3.1. A step function
The step function shown in Fig. 3.1 can be written as
f(t)=A1(t) (3.6)
and 1(t)isunit step function. This is defined as
1(t)=
1,t≥ 0
0,t<0
(3.7)
The Laplace transform of step function is
L{A1(t)} =
A
s
(3.8)
Proof:
L{A1(t)} =
∞
0
A1(t)e
−st
dt = A
∞
0
e
−st
dt
= A
−
1
s
e
−st
∞
0
= A
1
(−s)
(e
−s∞
− e
−s0
)
=
A
s
The Laplace transform of the unit step functions is
L{1(t)} =
1
s
(3.9)
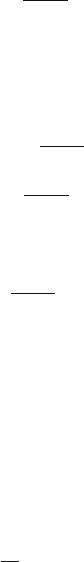
54 3 Analysis of Process Models
Exponential Function
The Laplace transform of an exponential function is of frequent use as expo-
nential functions appear in the solution of linear differential equations. Con-
sider an exponential function of the form
f(t)=e
−at
1(t) (3.10)
hence f(t)=e
−at
for t ≥ 0andf(t)=0fort<0. The Laplace transform of
this function is
L
e
−at
1(t)
=
1
s + a
(3.11)
Proof :
L
e
−at
1(t)
=
∞
0
e
−at
1(t)e
−st
dt =
∞
0
e
−(s+a)t
dt
= −
1
s + a
e
−(s+a)t
∞
0
=
1
s + a
From (3.10) follows that
L
e
at
1(t)
=
1
s −a
(3.12)
Ramp Function
Consider a ramp function of the form
f(t)=at1(t) (3.13)
The Laplace transform of this function is
L{at1(t)} =
a
s
2
(3.14)
Proof :
L{at1(t)} =
∞
0
at1(t)e
−st
dt
Let us denote u = at and ˙v =e
−st
and use the rule of integrating by parts
(˙uv)=u ˙v +˙uv
u ˙vdt = uv −
˙uvdt

3.1 The Laplace Transform 55
As ˙u = a and v = −
1
s
e
−st
, the Laplace transform of the ramp function is
L{at1(t)} =
at
1
(−s)
e
−st
∞
0
− a
∞
0
1
(−s)
e
−st
dt
=(0− 0) +
a
s
at
1
(−s)
e
−st
∞
0
=
a
s
2
Trigonometric Functions
Functions sin ωt and cos ωt are used in investigation of dynamical properties of
processes and control systems. The process response to input variables of the
form sin ωt or cos ωt is observed, where ω is the frequency in radians per time.
The Laplace transform of these functions can be calculated using integration
by parts or using the Euler identities
e
jωt
=cosωt +jsinωt
e
−jωt
=cosωt − jsinωt
e
jωt
+e
−jωt
= 2 cos ωt
e
jωt
− e
−jωt
=2jsinωt
(3.15)
Consider a trigonometric function of the form
f(t) = (sin ωt)1(t) (3.16)
The Laplace transform of this function is
L{(sin ωt)1(t)} =
ω
s
2
+ ω
2
(3.17)
Proof :
L{(sin ωt)1(t)} =
∞
0
(sin ωt)1(t)e
−st
dt =
∞
0
e
jωt
− e
−jωt
2j
e
−st
dt
=
∞
0
1
2j
e
−(s−jω)t
dt −
∞
0
1
2j
e
−(s+jω)t
dt
=
1
2j
e
−(s−jω)t
−(s −jω)
∞
0
+
1
2j
e
−(s+jω)t
−(s +jω)
∞
0
=
1
2j
1
s −jω
−
1
2j
1
s +jω
=
ω
s
2
+ ω
2
The Laplace transform of other functions can be calculated in a similar
manner. The list of the most commonly used functions together with their
Laplace transforms is given in Table 3.1.
56 3 Analysis of Process Models
Table 3.1. The Laplace transforms for common functions
f(t) F (s)
δ(t) - unit impulse function 1
1(t) - unit step function
1
s
1(t) − 1(t − T
v
),T
v
is a time constant
1−e
−sT
v
s
at1(t), a is a constant (ramp)
a
s
2
at
n−1
1(t),n>1 a
(n−1)!
s
n
e
−at
1(t)
1
s+a
1
T
1
e
−
t
T
1
1(t)
1
T
1
s+1
(1 − e
−at
)1(t)
a
s(s+a)
(1 − e
−
t
T
1
)1(t)
1
s(T
1
s+1)
1
a−b
(e
−bt
− e
−at
)
1(t), a, b are constants
1
(s+a)(s+b)
c−a
b−a
e
−at
+
c−b
a−b
e
−bt
1(t), c is a constant
s+c
(s+a)(s+b)
t
n−1
e
−at
(n−1)!
1(t),n≥ 1
1
(s+a)
n
1
a
t −
1−e
−at
a
2
1(t)
1
s
2
(s+a)
1
ab
+
1
a(a−b)
e
−at
+
1
b(b−a)
e
−bt
1(t)
1
s(s+a)(s+b)
c
ab
+
c−a
a(a−b)
e
−at
+
c−b
b(b−a)
e
−bt
1(t)
s+c
s(s+a)(s+b)
sin ωt 1(t), ω is a constant
ω
s
2
+ω
2
cos ωt 1(t)
s
s
2
+ω
2
e
−at
sin ωt 1(t)
ω
(s+a)
2
+ω
2
e
−at
cos ωt 1(t)
s+a
(s+a)
2
+ω
2
1 − e
−
ζt
T
k
cos
1 − ζ
2
t
T
k
+
ζ
1−ζ
2
sin
1 − ζ
2
t
T
k
1(t)
1
s(T
2
k
s
2
+2ζT
k
s+1)
0 ≤|ζ| < 1
1 −
1
√
1−ζ
2
e
−
ζt
T
k
sin
1 − ζ
2
t
T
k
+ ϕ
1(t)
1
s(T
2
k
s
2
+2ζT
k
s+1)
ϕ =arctan
√
1−ζ
2
ζ
, 0 ≤|ζ| < 1
