Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


39-12
attempts to establish a connection through the system
during a specific period of time, usually the busy hour.
The traffic capacity of a switch, switching network, or
trunk group is the traffic load that will, on the average,
provide the grade of service that is chosen as the service
objective.
For measurement purposes, it is sometimes easier to
observe the proportion of time that all circuits are busy
than to count the total of offered and carried calls (or
carried and lost calls). For the usual assumptions of
random calling, infinite sources, and a level value of
offered traffic, the proportion of calls blocked and the
proportion of time all circuits are busy are equal. This
relation does not persist for assumptions of peaked
traffic, smooth traffic, or limited sources.
Choice
of
Formula
The most important factors determining the choice of
formula for estimating grade of service are as follows:
A. The statistical nature of the call originations
Random from infinite sources
Random from finite sources
Peaked from infinite sources
Smooth from infinite sources
Periodic
B.
C.
The probability distribution of the call holding
time
The availability of the circuits serving the traffic
Full access
Limited access in a graded multiple
Limited access through a switching network
Lost calls cleared
Lost calls delayed
Lost calls held
Lost calls retried at a later time
D.
The behavior of calls when blocked
Traffic Equations
The two most commonly used equations in trunk
service estimation
are
the Erlang
B
and the Poisson. In
general, the Erlang
B
is a good estimator of single-hour
service, while the Poisson is a good estimator of the
service given
on
the average over a busy season during
which the offered load varies over a wider range than
would be expected from the assumptions of random
offered traffic.
In general, the use. of the Poisson
equation is not recommended for grades of service that
exceed
0.10
(10% blocking).
In small networks, it may be necessary to take limited
sources into account. This results in the Engset and
binomial equations as indicated below.
The Erlang B equation is given by
x=c
B(c,a)
=
(aC/c!)/
d/x!
x=o
The corresponding Engset equation for limited sources
is solved only by iterative techniques. Tables are avail-
able for this purpose.
*
The Poisson equation
is
given by
m
P(C,U)
=
e-a
2
(ax/x!)
x=c
The corresponding binomial equation is given by
Finally, the Erlang C equation is given by
C(c,a)
=
(a"c!)[c/(c
-
a)]/
c-
1
x=o
{
2
aX/x!
+
(a"c!)[c/(c
-
a)]}
where,
a
=
offered load in erlangs,
c
=
number of circuits,
n
=
number of limited sources less one,
r
=
load offered by an idle source.
Although the above equations are derived on the
assumption of a negative exponential distribution of
holding times, they are reasonable approximations for
most distributions encountered in practice.
The Erlang
B
equation is particularly useful in
estimating the load that will be carried on and overflow-
ing from a direct group of trunks to which random
traffic is offered. Calls that find all direct circuits busy
are directed to an alternate route. The traffic carried on
the direct route will be
a[l
-
B(c,a)],
and the traffic
overflowing will be
&(c,a),
where
a
=
the random
offered traffic. The overflow traffic is no longer random,
and other approximations are necessary to estimate the
grade of service given by an alternate trunk group to
overflow traffic. For this purpose, it is necessary to
estimate the variance of the overflow traffic, or more
conveniently, the ratio of the variance to the mean. This
latter quantity is known as the
peakedness
of the traffic.
(Random traffic from an infinite source has a peaked-
ness of one.) Peakedness,
z,
of traffic overflowing from
c
trunks offered
a
erlangs under the LCC assumptions is
given by:
z
=
1
-
aB(c,a)
+
a/[c
+
1
+
aB(c,a)
-
a]
When a number of overflow loads from a number of
direct groups are combined, the peakedness of the total
is given closely by
z
=
i:
zxa',li:
a',
x=
1
*=I
where
a',
is the overflow load from the xth source.
-
*Telephone Traflc Theory, Tables and Charts.
Berlin-
Munich: Siemens Aktiengesellschaft,
1970.
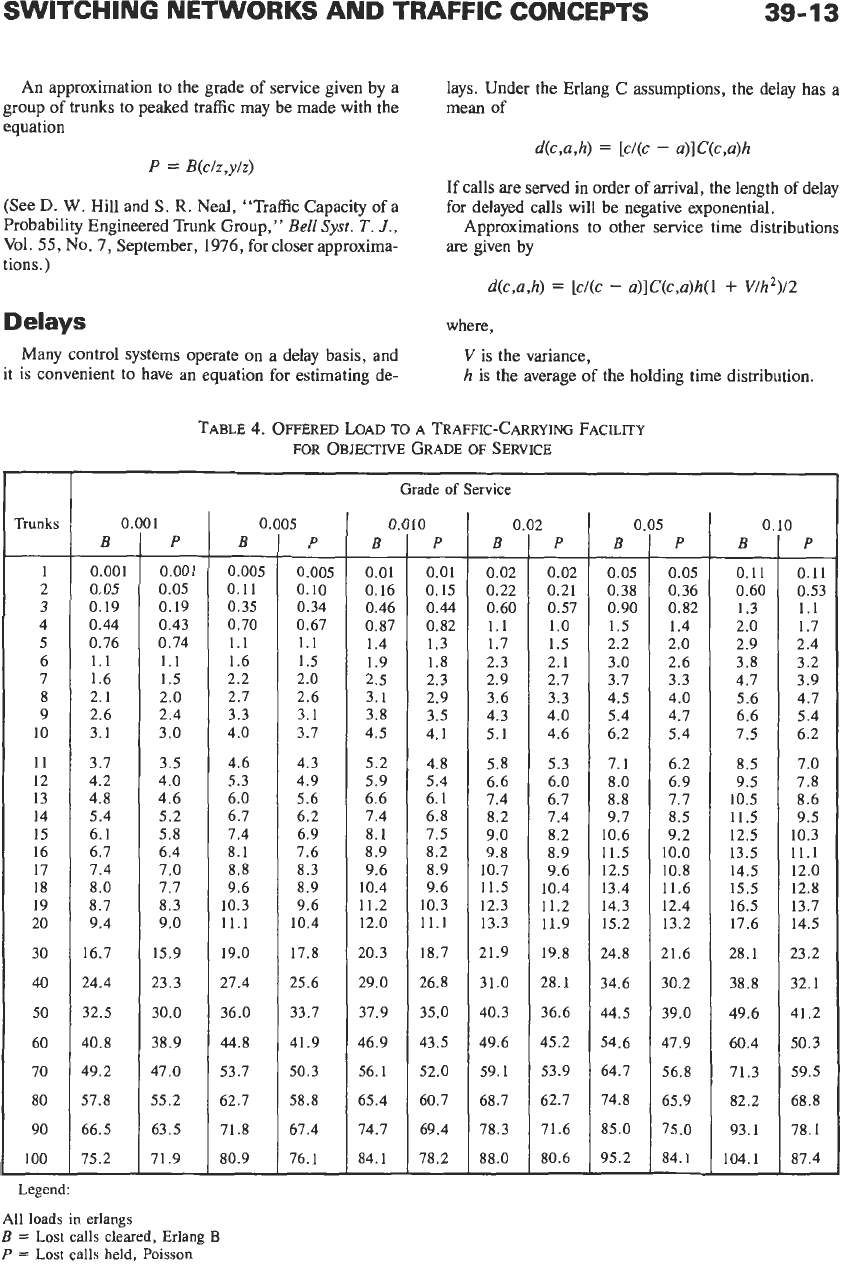
SWITCHING NETWORKS AND TRAFFIC CONCEPTS
39-13
Trunks
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
30
40
50
60
70
80
90
100
Legend:
An approximation to the grade
of
service given by a
group of trunks to peaked traffic may be made with the
equation
lays. Under the Erlang C assumptions, the delay has a
mean of
d(c,a,h)
=
[c/(c
-
u)]C(c,u)h
P
=
B(c/z,y/z)
(See
D.
W.
Hill and
S.
R.
Neal, “Traffic Capacity of a
Probability Engineered Trunk Group,”
Bell
Syst.
T.
J.,
Vol.
55,
No. 7, September, 1976, for closer approxima-
tions.)
If calls are served in order
of
arrival, the length of delay
for delayed calls will be negative exponential.
Approximations to other service time distributions
are
given by
d(c,u,h)
=
[c/(c
-
a)]C(c,u)h(l
+
V/h*)/2
Delays
where,
Many control systems operate on a delay basis, and
it
is
convenient to have an equation for estimating de-
V
is
the variance,
h
is the average
of
the holding time distribution.
0.
B
0.001
0.05
0.19
0.44
0.76
1.1
1.6
2.1
2.6
3.1
3.7
4.2
4.8
5.4
6.1
6.7
7.4
8.0
8.7
9.4
16.7
24.4
32.5
40.8
49.2
57.8
66.5
75.2
TABLE
4.
OFFERED LOAD
TO
A
TRAFFIC-CARRYING
FACILITY
FOR
OBJECTIVE GRADE
OF
SERVICE
5
P
0.005
0.10
0.34
0.61
1.1
1.5
2.0
2.6
3.1
3.7
4.3
4.9
5.6
6.2
6.9
7.6
8.3
8.9
9.6
10.4
17.8
25.6
33.1
41.9
50.3
58.8
61.4
76.1
0.
B
0.01
0.16
0.46
0.87
1.4
1.9
2.5
3.1
3.8
4.5
5.2
5.9
6.6
7.4
8.1
8.9
9.6
10.4
11.2
12.0
20.3
29.0
37.9
46.9
56.1
65.4
74.7
84.1
1
P
0.001
0.05
0.19
0.43
0.74
1.1
1.5
2.0
2.4
3.0
3.5
4.0
4.6
5.2
5.8
6.4
7.0
7.7
8.3
9.0
15.9
23.3
30.0
38.9
47.0
55.2
63.5
71.9
0.1
B
0.005
0.11
0.35
0.70
1.1
1.6
2.2
2.7
3.3
4.0
4.6
5.3
6.0
6.7
7.4
8.1
8.8
9.6
10.3
11.1
19.0
27.4
36.0
44.8
53.7
62.7
71.8
80.9
Grade
of
Service
0
P
0.01
0.15
0.44
0.82
1.3
1.8
2.3
2.9
3.5
4.1
4.8
5.4
6.1
6.8
1.5
8.2
8.9
9.6
10.3
11.1
18.7
26.8
35.0
43.5
52.0
60.7
69.4
78.2
-
-
0.
B
0.02
0.22
0.60
1.1
1.7
2.3
2.9
3.6
4.3
5.1
5.8
6.6
7.4
8.2
9.0
9.8
10.7
11.5
12.3
13.3
21.9
31.0
40.3
49.6
59.1
68.7
78.3
88.0
-
-
!
P
0.02
0.21
0.57
1.0
1.5
2.1
2.7
3.3
4.0
4.6
5.3
6.0
6.7
7.4
8.2
8.9
9.6
10.4
11.2
11.3
19.8
28.1
36.6
45.2
53.9
62.1
71.6
80.6
-
0
B
0.05
0.38
0.90
1.5
2.2
3.0
3.7
4.5
5.4
6.2
I.
1
8.0
8.8
9.7
10.6
11.5
12.5
13.4
14.3
15.2
24.8
34.6
44.5
54.6
64.7
74.8
85.0
95.2
-
5
P
0.05
0.36
0.82
1.4
2.0
2.6
3.3
4.0
4.7
5.4
6.2
6.9
7.7
8.5
9.2
10.0
10.8
11.6
12.4
13.2
21.6
30.2
39.0
47.9
56.8
65.9
75.0
84.1
-
0.
B
0.11
0.60
1.3
2.0
2.9
3.8
4.7
5.6
6.6
7.5
8.5
9.5
10.5
11.5
12.5
13.5
14.5
15.5
16.5
17.6
28.1
38.8
49.6
60.4
71.3
82.2
93.1
104.1
)
P
0.11
0.53
1.1
1.7
2.4
3.2
3.9
4.1
5.4
6.2
7.0
7.8
8.6
9.5
10.3
11.1
12.0
12.8
13.1
14.5
23.2
32.1
41.2
50.3
59.5
68.8
78.1
87.4
-
All loads
in
erlangs
B
=
Lost
calls cleared, Erlang
B
P
=
Lost
calls held,
Poisson

39-14
REFERENCE
DATA
FOR ENGINEERS
For calls served in order of arrival, the negative expo-
nential
is
an approximation to the delay distribution of
delayed calls.
Table
4
gives values of loads for objective losses over
a range of loads and trunks for the Poisson and Erlang B
formulas. For computer use, advantage can be taken of
the following recurrence relation for computing the
infinite source loss formulas:
Let
E(c
+
1,a)
=
(c/a)[E(c,a)
+
11
and
E(0,a)
=
1
Then for lost calls cleared
B(c,a)
=
l/E(c,a)
and for lost calls delayed
C(c,a)
=
l/{[(c
-
a)/c][E(c,a)
-
11
+
1)
For
lost
calls held:
Let
D(c,a)
=
[(a/c)
+
1]D(c
-
1,a)
and
D(-1,a)
=
0
D(0,a)
=
1
-
(a/c)D(c
-
2,a)
Then
&,a)
=
1
-
e-'
D(c
-
1,a)
REFERENCES
Telephone TrafJic Theory, Tables and Charts.
Berlin-
Munich: Siemens Aktiengesellschaft,
1970.
(In
English and German.)
Bear,
D
.
Principles in
Telecommunications-Trafic
Engineering.
Peter Peregrinus, Ltd.,
1976
(Repr.
1980).
Mina, R.
Introduction to Teletrafic Engineering.
Te-
lephony Publishing
Co.,
1974.

40
Electroacoustics
Revised and Expanded
by
Paul
D.
Schomer
and George
W.
Swenson,
Jr.
Theory of Sound Waves
40-3
Wave Equation
Sound in Gases
Sound in Liquids
Sound in Solids
Sound Intensity
Sound-Pressure Level (SPL)
Electrical Analogies for Acoustical and/or Mechanical
Systems
40-5
Hearing
40-6
Measurement of Sound
40-8
Sound Level Meters
Measurement and/or Laboratory Microphones and Their
Sound Level
Sound Power Level
Calibration
Definitions
40-9
Environmental Noise
40-10
Assessment
of
Workplace-Industrial Noise
40-12
Sound
in Enclosed Rooms
40-12
Standing Sound Waves
Reverberation Time
Measurement
of
Reverberation Time
Calculation
of
Reverberation Time
Absorption Coefficients
Optimum Reverberation Time
40-
1

40-2
REFERENCE
DATA
FOR ENGINEERS
Indoor Design Noise Levels and Speech Communication
40-15
Preferred Speech Interference Levels/Speech Interference Levels
Interior Design Noise Levels
Sound
Isolation
40-17
Walls
Doors
Resilient Channels
Weighting of Components
Flanking
Leaks
Sound-Reinforcement Systems
40-23

THEORY
OF
SOUND
WAVES*
Sound (or a sound wave) is an alteration in pressure,
stress, particle displacement, or particle velocity that is
propagated in an elastic material, or the superposition
of such propagated alterations. Sound (or sound sensa-
tion) is also the sensation produced through the ear by
the above alterations.
Wave Equation
The behavior of small-amplitude sound waves is
given by the wave equation
v’p
=
(l/c’)(a’p/at2)
(Eq.
1)
where,
p
is the instantaneous pressure increment above
t
is the time in seconds,
c
is the velocity of propagation in meterdsecond,
V2
is the Laplacian.
The quantity
p
is a function of time and of the three
coordinates of space. For the particular case
of
rectan-
gular coordinates x, y, and
z
(in meters), the Laplacian
is given by
and below a steady pressure (pascals),
v2
=
(a’/ax’)
+
(a’/ay2)
+
(a’/az2)
(Eq.
2)
Plane Waves-For a plane wave of sound, where
variations with respect to
y
and
z
are zero,
V’p
=
a2p/ax2
=
d’p/dx’;
the latter is approximately equal to
the curvature of the plot of
p
versus
x
at some instant.
Equation
1
states simply that, for variations in
x
only,
the acceleration in pressure
p
(which is the second time
derivative of
p)
is proportional to the curvature in
p
(which is the second space derivative of
p).
Sinusoidal variations in time are usually
of
interest.
For this case, the standard procedure is to put
p
=
(real
part of
jTeJ*f),
where the phasor
j?
now satisfies the
equation
0’3
+
(m/c)’p
=
0
(Eq.
3)
The velocity phasor
V
of the sound wave in the
medium is related to the complex pressure phasor
p
by
V
=
-(l/jwpo)
grad
jT
(Eq.
4)
The specific acoustic impedance
z
at any point in the
medium is the ratio of the pressure phasor to the
velocity phasor, or
z
=
p/V
Spherical Waves-The solutions of equations 1
and 3 take particularly simple and instructive forms for
the case of one-dimensional plane and spherical waves
in one direction. Table 1 summarizes the pertinent
information.
For example, the acoustic impedance for spherical
waves has an equivalent electrical circuit comprising a
resistance shunted by an inductance. In this form, it is
obvious that a small spherical source
(r
is small) cannot
radiate efficiently since the radiation resistance
poc
is
shunted by a small inductance
por.
Efficient radiation
begins approximately at the frequency where the resist-
ance
poc
equals the inductive (mass) reactance
for.
This
is the frequency at which the period
(llf)
equals
the time required for the sound wave to travel the
distance
2m.
Sound
in Gases
The acoustic behavior
of
a medium is determined by
its physical characteristics and, in the case of gases, by
the density, pressure, temperature, specific heat, coeffi-
cients of viscosity, and the amount of heat exchange at
the boundary surfaces.
The velocity of propagation in a gas is a function of
the equation of state
(PV
=
RT
plus higher-order
terms), the molecular weight, and the specific heat.
*
For small displacements relative to the wavelength of
sound, the velocity is given by
where,
y
=
ratio of the specific heat at constant pressure
to that at constant volume,
po
=
the steady pressure of the gas in
newtons/meter2,
po
=
the steady or average density of the gas in
kilograms/meter3
.
The values of the velocity in a few gases are given in
Table
2
for
0
degrees Celsius and
760
millimeters of
mercury barometric pressure.
The velocity of sound,
c,
in dry air is given by the
experimentally verified equation
c
=
331.45
k
0.05
meterslsecond
=
1087.42
-t
0.16 feethecond
for the audible-frequency range, at
0
degrees Celsius
and 760 millimeters of mercury with 0.03-mole-percent
content of C02.
*
Hardy,
H.
C.,
Telfair,
D.,
and Pielemeier,
W.
H.
“The
Velocity of Sound in Air.”
Journal
of
the Acoustical Society
of
America,
Vol.
13,
January 1942,
pp.
226-233. See also
Beranek, L.
Acoustic Measurements.
New York: John Wiley
&
Sons,
Inc., 1949,
p.
46.
*
Rayleigh, Lord.
Theory
of
Sound.
Vols. 1 and 2. New
York
Dover
Publications, 1945. Morse, P. M.
Vibrution
&
Sound.
2d ed. New York McGraw-Hill Book
Co.,
1948.

40-4
REFERENCE
DATA
FOR ENGINEERS
Factor
Equation for
p
Equation for
j
Solution for
p
Solution for
j
Solution for
5
-
Z
Equivalent
Electrical
-
Circuit
for
Z
TABLE
1.
SOLUrIONS
FOR VARIOUS PARAMETERS
Type
of Sound Wave
__
Plane Wave
a2piax2
=
(iic2)(a2p/at2)
(d2jldx2)
+
(w/c)’P
=
0
p
=
F[t
-
(xlc)]
-
j
=
P
exp
(-jwxlc
+
jl3)
V
=
(p/poc)
exp
(-jwxlc
+
jl3)
z
=
poc
Spherical Wave
~
(a2piax2)
+
(2/r)(ap/ar)
=
(1/c2)(a2p/at2)
(d’jldx’)
+
(2/r)(dj/dt)
+
(w/d2p
=
0
p
=
(llr)
F[t
-
(xlc)]
j
=
(l/r)
F
exp
(-jwr/c
+
je)
C
=
(p/pocr) [l
+
(cljwr)]
exp
(-jw
r/c
+
jl3)
Z
=
poc/[l
+
(cijwr)]
2-
I
p
=
excess pressure in pascals (newtonsimeter’)
j
=
complex excess pressure in pascals (newtons/meter2)
t
=
time in seconds
x
=
space coordinate for plane wave in meters
r
=
space coordinate for spherical wave in meters
5
=
complex velocity in meterslsecond
2
=
specific acoustic impedance in rayls (newton-seconds/meter3)
c
=
velocity
of
propagation in meterslsecond
w
=
2rrh
f
=
frequency in hertz
F
=
an arbitrary function
0
=
phase constant
po
=
density
of
medium in kilograms/meter3
P
=
peak amplitude of the phasor (units dependent on wave type)
The velocity in air for a range of about
20
degrees
Celsius change
in
temperature
is
given approximately by
c
=
331.45
+
0.607Tc meters/second
=
1052.03
+
1.106Tf feethecond
where
T,
is the temperature in degrees Celsius and
Tf
is
the temperature in degrees Fahrenheit. For values of
T,
greater than 20 degrees, the following equation may be
used:
c
=
33 1.45
X
(Tk/273)
”’
meterdsecond
where
Tk
is the temperature in kelvins.
reference should be made to the literature.*
For
other corrections, if extreme accuracy is desired,
*
Hardy,
H.
C.,
Telfair,
D.,
and Pielemeier, W.
H.
“The
Velocity of Sound in Air.”
Journal
of
the
Acoustical
Society
of
America,
Vol.
13,
January
1942,
pp.
226-233.
From Equation
5
and Table 1, characteristic imped-
ance is equal to
the
ratio of the
sound
pressure to the
particle velocity.
z
=
ji/G
=
poc cos4
For plane waves,
4
=
0
and cos4
=
1. For spherical
waves, tan4
=
A/2m,
where
A
=
wavelength of the
acoustic wave, and
r
=
distance from the sound source.
For
r
greater than a few wavelengths, cos4
=
1.
Characteristic impedance poc in newton-seconds1
meter3 for several ,gases at
0
degrees Celsius and 760
millimeters of mercury is given in Table
2.
Sound
in
Liquids
In liquids, the velocity of sound is given approxi-
mately by
c
=
(1/Kpo)”2

ELECTROACOUSTICS
40-5
Air, dry
Argon
Carbon dioxide
Carbon monoxide
Helium
Hydrogen
Neon
Nitrogen
TABLE
2.
GASES
1.293 331.45 0.59 428.6
A
1.783 319 0.56
596
COZ
1.977
259 0.4 511
co
1.25
338 0.6 42 1
He
0.178
965 0.8 173.2
H2
0.0899
1284 2.2 114
Ne
0.900 435 0.8
383
N2
1.251 334 0.6
418
where,
c
is the velocity in meters/second,
K
is the compressibility in meter-seconds’
/
kilogram and may be regarded as constant.
For most liquids,
K
=
(47
X
10-8)/981
Figures for the velocity
of
sound in meterdsecond
through some liquids are given in Table
3.
Sound in Solids
See Chapter
4,
Tables
17,
18,
and 19.
Sound Intensity
The sound intensity is the average rate of sound
energy transmitted in a specified direction through a
unit area normal to this direction at the point consid-
ered. Intensity is a vector quantity. In the case of a plane
or spherical wave (several wavelengths from the source)
in a fluid, the intensity in the direction of propagation is
given by
z
=
p2/pc
(Eq.
7)
The units of
I
are wattdmeter’
Sound-Pressure Level
(SPL)
It is sometimes convenient to use the decibel scale to
express the ratio between any two sound intensities.
Since sound pressure is usually proportional to the
square root of the corresponding sound intensity,
sound-pressure level (SPL) is defined as
SPL
=
10
loglo
(p’/p;)
(Eq.
8)
where
po
is
20
micropascals in air.*
At times, sound pressure is measured in units other
than pascals. Table
4
lists the
SPL
for a quantity of one
in these other units (e.g., 1 atmosphere).
ELECTRICAL ANALOGIES FOR
ACOUSTICAL AND/OR
MECHANICAL SYSTEMS””
Analysis of electromechanical-acoustical transduc-
ers, mechanical systems, or acoustical systems can he
facilitated by the use
of
electrical analogies. Two forms
of
electrical analogies are possible:
(1)
force
or
pres-
-
*
The reference
of
1
micropascal is usually used for liquids
**
Swenson, George W. Principles
of
Modern Acoustics.
and
all
other media.
New York: Van Nostrand,
1953.
TABLE
3.
VELOCITY
OF
SOUND
IN
LIQUIDS
Temperature Velocity in
Liquid in
“C
(dS)
x
103
Alcohol, ethyl
12.5 1.24
20 1.17
Mercury
20 1.45
Petroleum
15 1.33
Water, fresh
17 1.43
Water, sea
(36
parts/thousand salinty)
15 1.505

40-6
SPL
94
127.6
170.8
194.1
14
REFERENCE
DATA
FOR ENGINEERS
Unit
1
pascal (Pa, N/m’)
1
pound/foot’ (PSf)
1
poundh’ (psi)
1 atmosphere (atm)
1
microbar (@a*)
TABLE
4.
SOUND-PRESSURE LEVELS
FOR
SEVERAL
UNITS
USED
To
MEASURE SOUND PRESSURE
IN
AIR (RE
20
MICROPASCALS)
~
Velocity (meters/second)
Displacement (meters)
Volume Velocity
(meters3 second-’) Current (amperes)
Volume Displacement
(meters
3,
Charge (coulombs)
sure-voltage analogue and
(2)
force or pressure-current
analogue. Tables
5
and
6
tabulate the pertinent quanti-
ties in these two analogies.
In a specific problem in which it is desired to
represent an acoustical or mechanical system by an
electrical circuit, a choice must be made between the
force-voltage and force-current analogies. If the system
includes electrical as well as mechanical or acoustical
elements, as in a motor or a loudspeaker, for example,
the choice is dictated by the type of coupling between
the electrical and mechanical parts. However, if the
system
is
entirely mechanical or acoustical, the choice
is arbitrary and depends upon personal preference. In
any event, given the equivalent circuit derived on the
basis of one analogy, the equivalent circuit correspond-
ing to the other analogy can be derived by taking the
dual of the given circuit.
In a system that combines acoustical and mechanical
quantities, it is necessary to establish a common frame
of reference. Usually, it is easiest to convert acoustical
quantities to mechanical quantities, as for example,
integrating the pressure over a piston (loudspeaker or
microphone) to calculate the force, etc.
HEARING*
The auditory system consists of the periphery sen-
sors, acoustic neurological transducers, the ears, the
eighth cranial nerve leading to a programming and
priority switching center at various levels of the brain
stem, and finally to the auditory area of the cortex
located near the Sylvian fissure of the frontal-lobe
convolution.
The auditory system does much more than detect
minute sounds. Among other functions, it preferentially
places more weight on certain preprogrammed charac-
teristic sounds, localizes the direction of most sounds
by a variety of ingenious techniques,
and initiates
involuntary actions for visual acquisition of the source.
The hearing mechanism was probably evolved to help
man survive in a hostile environment,
and not for
linguistic communication or for musical entertainment.
*
Flanagan,
J.
L.
Speech Analysis, Synthesis and Percep-
tion.
New York Academic Press, 1965. Also Richardson,
E.
G.,
ed.
Technical Aspects
of
Sound.
New York: Elsevier
Press, 1953.
TABLE
5.
FORCE/PRESSURE-VOLTAGE ANALOGY
~~
Mechanical Quantity
I
Acoustical Quantity
I
Electrical Quantity
Force (newtons)
I
Sound Pressure
(newtons meter-’)
I
Voltage (volts)
Mass
(kilograms)
I
Acoustic Mass
Inductance
(kilograms meter-4)
I
(henrys)
Stiffness
(newtonsimeter)
I
i
Acoustic Stiffness Capacitance-’
(kilograms meter-4 second-’)
(farads
-
l)
Viscous Friction Acoustic Resistance
I
(newtons/meter/second) (kilograms meter-4 second-’)
I
Resistance (ohms)
Mechanical Impedance
(mechanical ohms) or
(forceivelocity)
Acoustic Impedance
(kilograms meter-4 second-’)
Impedance (ohms)
ELECTROACOUSTICS
Mechanical Quantity
Force (newtons)
40-7
Acoustical Quantity Electrical Quantity
Sound Pressure
(newtons meter-2) Current (amperes)
TABLE
6.
FORCE/PRESSURE-CURRENT ANALOGY
Displacement (meters)
Impulse
I
v
dt
Volume Displacement
(meters
3,
(volt-seconds)
Volume Velocity
Velocity (meterdsecond) (meters3 second-')
Mass (kilograms)
Stiffness
(newtondmeter)
I
Voltage (volts)
~
Acoustic Mass Capacitance
(kilograms meterF4) (farads)
Acoustic Stiffness Inductance
-
(kilograms meter-4 second-*) (henry-')
Mechanical Impedance
(mechanical ohms) or
(force/velocity)
Acoustic Impedance
(kilograms meter-4 second-') Admittance (mhos)
Viscous Friction Acoustic Resistance Conductance
(newtonshnetedsecond)
(kilograms meter-4 second-')
I
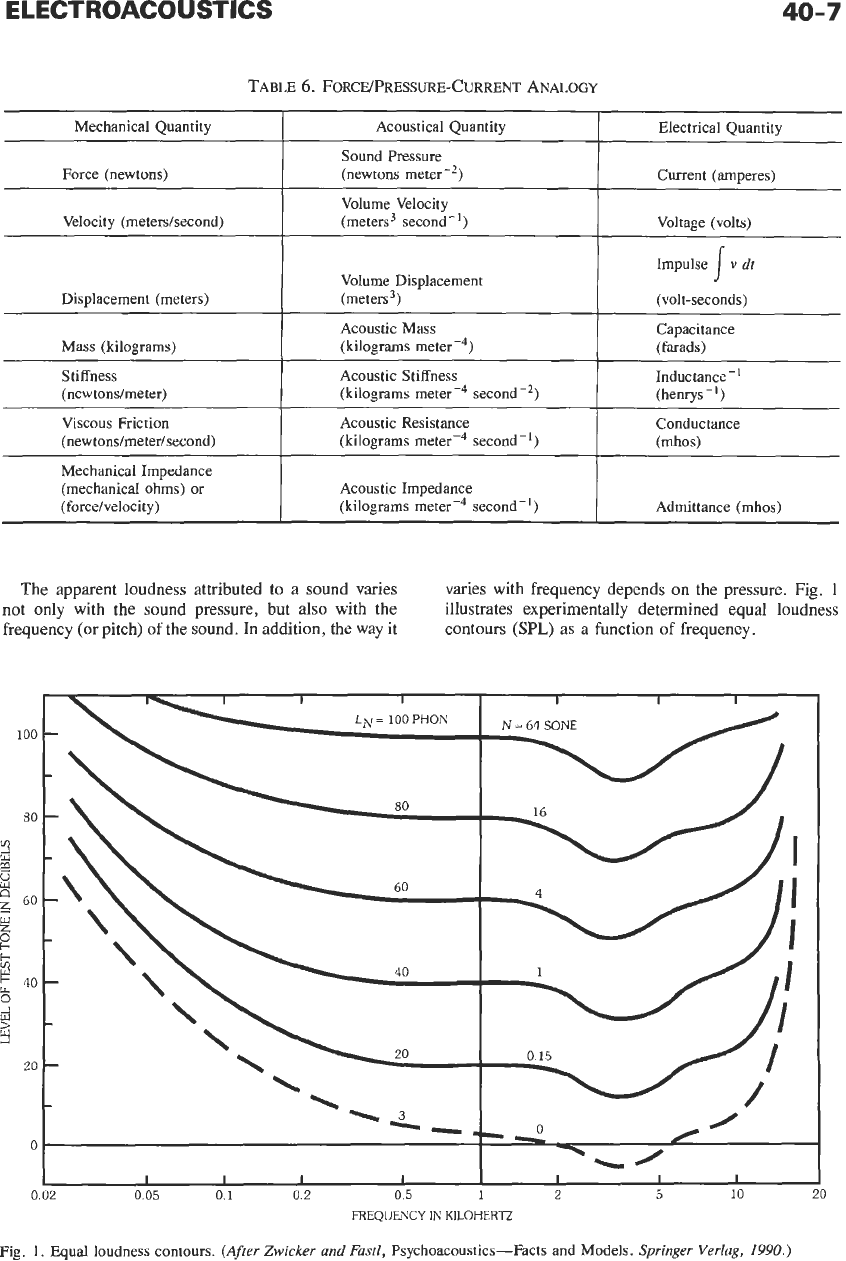
The apparent loudness attributed to a sound varies
not only with the sound pressure, but
also
with the
frequency
(or
pitch) of the sound. In addition, the way it
varies with frequency depends on the pressure. Fig.
1
illustrates experimentally determined equal loudness
contours
(SPL)
as
a function of frequency.
Fig.
1.
Equal
loudness contours.
(After
Zwicker
and
Fustl,
Psychoacoustics-Facts and
Models.
Springer
Verlug,
1990.)
