Menke W. Geophysical Data Analysis: Discrete Inverse Theory

Подождите немного. Документ загружается.

168

Factor

Analysis

tion of a set of orthogonal factors. Even when the factors have no

obvious physical interpretation, the decomposition can be useful as a

tool for quantifying the similarities between the

vectors. This kind of

factor analysis is often called

empirical orthogonal function analysis.

an example of this application of factor analysis, consider the set

shapes shown in Fig.

10.5.

These shapes might represent

profiles of mountains or other subjects of interest. The problem we

shall consider

how these profiles might

ordered to bring out the

similarities and differences between the shapes.

geomorphologist

might desire such an ordering because, when combined with other

kinds of geological information, it might reveal the kinds of erosional

processes that cause the shape of mountains to evolve with time.

Fig.

10.5.

set

hypothetical mountain profiles. The variablity

shape

will

determined using factor analysis.

10.4

Empirical Orthogonal Function Analysis

169

Fig.

10.6.

The three largest factors

in the representation

the profiles in Fig.

10.5,

with their corresponding singular values

A,.

(a) The first factor represents an average

mountain profile, with

3.29;

(b)

the second, the asymmetry

the mountain, with

I.,

1.19:

/I,

We begin by discretizing each profile and representing it as a unit

vector (in this case of length

1).

These unit vectors make up the

matrix

on which we perform factor analysis. Since the factors do not

represent any particular physical object, there is no need to impose any

positivity constraints on them, and we use the untransformed singu-

lar-value decomposition factors. The three most important factors

(that is, the ones with the three largest singular values) are shown in

Fig.

10.6.

The first factor, as expected, appears to be simply an

“average” mountain; the second seems to control the skewness, or

1.0

-1.0

-4-

Fig.

10.7.

The mountain profiles

Fig.

10.5

arranged according to the relative

amounts of factors

and

contained in each profile’s orthogonal decomposition.

170

Factor

Analysis

degree of asymmetry,

the mountain; and the third, the sharpness of

the mountain’s summit. We emphasize, however, that this interpreta-

tion was made after the factor analysis and was not based on any a

priori notions

how mountains might differ. We can then use the

factor loadings as a measure of the similarities between the mountains.

Since the amount of the first factor does not vary much between

mountains, we use a two-dimensional ordering based on the relative

amounts of the second and third factors in each of the mountain

profiles (Fig.

10.7).

CONTINUOUS INVERSE

THEORY AND TOMOGRAPHY

11.1

The Backus -Gilbert Inverse Problem

While continuous inverse problems are not the main subject of this

book, we will cover them briefly to illustrate their relationship to dis-

crete problems. Discrete and continuous inverse problems differ in

their assumptions about the model parameters. Whereas the model

parameters are treated as a finite-length vector in discrete inverse

theory, they are treated as a continuous function in continuous inverse

theory. The standard form of the continuous inverse problem is

di=

1.“

Gi(z)m(z) dz

(1 1.1)

when the model function

m(z)

varies only with one parameter, such as

depth

When the model function depends on several variables, then

Eq.

(

1.1)

must be generalized to

Gi(x)m(x) dV,

(11.2)

1”

where

dV,

is the volume element in the space of

The “solution”

a discrete problem can be viewed as either an

estimate of the model parameter vector

or a series of weighted

averages of the model parameters,

mavg

Rm-,

where

is the resolu-

tion matrix (see Section

4.3).

If the discrete inverse problem is very

underdetermined, then the interpretation of the solution in terms of

weighted averages is most sensible, since a single model parameter is

171

172

Continuous Inverse Theory

and

Tomography

very poorly resolved. Continuous inverse problems can be viewed as

the limit of discrete inverse problems as the number of model parame-

ters becomes infinite, and they are inherently underdetermined. At-

tempts to estimate the model function

m(x)

at a specific point

are futile. All determinations of the model function must be made in

terms of local averages, which are simple generalizations of the discrete

case,

myg

X.G:gd.

JUJ

Z.R..m-"

JUJ

where

X.,G-,BG,:

rnavB(xo)

GTg(x0)

R(xo,x)rnhe(x) dVx

1.3)

where

R(xo,x)

GTg(xo)Gi(x)

Here

G;g(xo)

is the continuous analogy to the generalized inverse

Gig

and the averaging function

R(xo ,x)

(often called the resolving kernel) is

the analogy to

The average is localized near the target point

if the

resolving kernel is peaked near

xo.

The solution of the continuous

inverse problem involves constructing the most peaked resolving ker-

nel possible with a given set

measurements (that is, with a given set of

data kernels,

Gi(x)).

The spread ofthe resolution function is quantified

by [compare with

Eq.

(4.23)]:

1.4)

Here

w(xo,x)

is a nonnegative function that is zero at the point

and

that grows monotonically away from that point. One commonly used

choice is the quadratic function

w(xo,x)

Ixo

x12.

Other, more

complicated functions can be meaningful if the elements of

have an

interpretation other than spatial position. After inserting the definition

of the resolving kernel

[Eq.

1.3), second line] into the definition of

the spread

[Eq.

1.4)], we find

4x0)

~vw~xo,x~R~xo,x~R~xo,x~

dvx

r-1

w(x0

,x)

GTg(xo)Gi(x)

Gjg(xo)Gj(x)

dvx

c c

Gr"(xo)G~~(xo)[~,(xo)l

(11.5)

i-1

j-1

1.2

Resolution and Variance Trade-off

173

where

(11.6)

The continuous spread function has now been manipulated into a

form completely analogous to the discrete spread function in Eq.

(4.24).

The generalized inverse that minimizes the spread

the resolu-

tion is the precise analogy of Eq.

(4.32).

11.2

Resolution and Variance Trade-off

Since the data

are determined only up to some error quantified by

the covariance matrix [cov d], the localized average rna"B(xo) is deter-

mined up to some corresponding error

var[mavB(xo)]

GFg(x0)[cov dlijGj-g(x0)

1.8)

i-1

j-1

in the discrete case, the generalized inverse that minimizes the

spread of resolution may lead to a localized average with large error

bounds.

slightly less localized average may

desirable because it

may have much less error. This generalized inverse may be found by

minimizing a weighted average of the spread of resolution and size

variance

minimize J'(xo)

w(xo,x)R2(xo,x)

dV,

~ar[~~B(x~)]

1.9)

The parameter

which varies between

and 1, quantifies the relative

weight given to spread of resolution and size

variance.

in the

discrete case (see Section

lo), the corresponding generalized inverse

can be found by using Eq. (1

1.7),

where all instances of [Sij(xo)] are

replaced by

[S;(xO)]

w(x0 ,x)Gi(x)Gj(x)

dV,

a)[cov dIij (1 1.10)

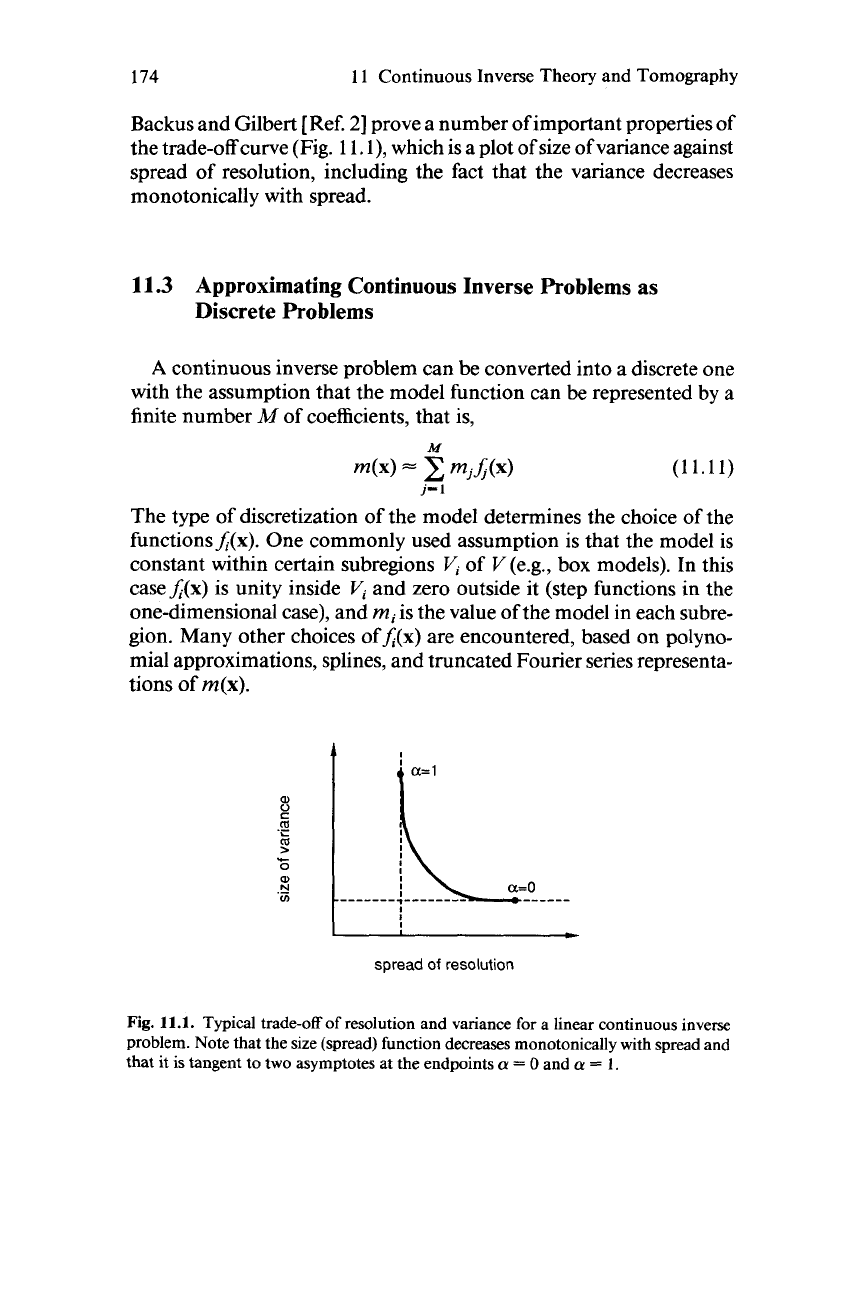
174

Continuous Inverse Theory

and

Tomography

Backus and Gilbert [Ref.

prove a number of important properties of

the trade-off curve (Fig.

l),

which is a plot of size of variance against

spread of resolution, including the fact that the variance decreases

monotonically with spread.

11.3

Approximating Continuous Inverse Problems as

Discrete Problems

continuous inverse problem can be converted into a discrete one

with the assumption that the model function can

represented by a

finite number

coefficients, that

is,

m(x)

mjJ(x)

(11.11)

The type of discretization of the model determines the choice of the

functionsfi’(x). One commonly used assumption is that the model

constant within certain subregions of

(e.g., box models). In this

casefi’(x) is unity inside

and zero outside it (step functions in the

one-dimensional case), and

is the value

the model in each subre-

gion. Many other choices ofA(x) are encountered, based on polyno-

mial approximations, splines, and truncated Fourier series representa-

tions

m(x).

spread of

resolution

Fig.

11.1.

Typical trade-off of resolution and variance for a linear continuous inverse

problem. Note that the size (spread) function decreases monotonically with spread and

that it is tangent to two asymptotes at the endpoints

and

1.3

Continuous Inverse Problems

Discrete Problems

175

Inserting Eq.

(

1.1

into the canonical continuous problem [Eq.

1.2)]

leads to a discrete problem

[

/vGi(x)$(x)

dVx

G,mj

(1 1.12)

where the discrete data kernel is

G,y

G~(x)$(x)

dVx

1.13)

In the special case of the model function presumed to

constant in

subregions

(centered, say, on the points

xi),

Eq.

(1 1.13)

be-

comes

G..

Gi(x)

d~x

(11.14)

the data kernel vanes slowly with position

that it is approximately

constant in the subregion, then we may approximate the integral as just

its integrand evaluated at

times the volume

Go=

Gi(x)

dVx

Gi(xj)Q

(11.15)

Two different factors control the choice of the size ofthe subregions.

The first is dictated by an

priori

assumption of the smoothness of the

model. The second becomes important only when one uses Eq.

(

1.15)

in preference to Eq.

(

1.14).

Then the subregion must be small enough

that the data kernels

G,(x)

are approximately constant in the subre-

gion. This second requirement often forces the subregions to

much

smaller than dictated by the first requirement,

Eq.

(

1.14)

should

used whenever the data kernels can be analytically integrated. Equa-

tion

(

15)

fails completely whenever a data kernel has an integrable

singularity within the subregion. This case commonly arises in prob-

lems involving the use of seismic rays to determine acoustic velocity

structure.

176

Continuous

Inverse

Theory

and

Tomography

11.4

Tomography and

Continuous

Inverse Theory

The term “tomography” has come to be used in geophysics almost

synonymously with the term “inverse theory.” Tomography is derived

from the Greek word

tornos,

that

is,

slice, and denotes forming an

image of an object from measurements made from slices (or rays)

through it. We consider tomography a subset of inverse theory, distin-

guished by a special form

the data kernel that involves measure-

ments made along rays. The model function in tomography is a func-

tion of two or more variables and is related to the data by

ICi

rn[X(S),Y(S)I

1.16)

Here the model function is integrated along a ray

having arc length

This integral is equivalent to the one in a standard continuous problem

[

Eq.

1.2)] when the data kernel is

G,(x,y)

6{x(s)

x,[y(s)]>

ds/dy,

where

6(x)

is the Dirac delta function:

(11.17)

Here

xis

supposed to vary with

along the curve

and y is supposed to

vary with arc length

While the tomography problem is a special case of a continuous

inverse problem, several factors limit the applicability of the formulas

of the previous sections. First, the Dirac delta functions in the data

kernel are not square integrable,

that the S,[“overlap” integrals; see

Eq.

1.6)] have nonintegrable singularities at points where rays inter-

sect. Furthermore, in three-dimensional cases the rays may not inter-

sect at all,

that all the

may be identically zero. Neither

these

problems is insurmountable, and they can be overcome by replacing

the rays with tubes of finite cross-sectional width. (Rays are often an

idealization of a finite-width process anyway, as in acoustic wave prop-

agation, where they are an infinitesimal wavelength approximation.)

Since this approximation is equivalent to some statement about the

smoothness of the model function

m(x,y),

it often suffices to discretize

the continuous problem by dividing it into constant

subregions,

where the subregions are large enough to guarantee a reasonable num-

1.5

Tomography and the Radon Transform

177

ber containing more than one ray. The discrete inverse problem is then

ofthe

form

ZjG,mj, where the data kernel Gijgives the arc length

the ith ray in thejth subregion. The concepts

resolution and

variance, now interpreted in the discrete fashion

Chapter

are still

applicable and

considerable importance.

11.5

Tomography and

the

Radon Transform

The simplest tomography problem involves straight-line rays and a

two-dimensional model function

m(x,y)

and is called Radon's prob-

lem.

historical convention, the straight-line rays

Eq.

(

1.6)

are

parametrized by their perpendicular distance

from the origin and the

angle

(Fig.

1.2)

that the perpendicular makes with the

axis. Posi-

tion

(XJ)

and ray coordinates

(u,s),

where

is arc length, are related by

(;)=(cos~ -sine)(;)

(;)

(

cos

sin

8)(")

sin

cos

-sin

cos

(11.18)

The tomography problem is then

m(x

cos

sin

cos

(11.19)

Fig.

11.2. The Radon transform is performed

integrating

function

(x,y)

along

straight lines (bold) parameterized

their arc length

perpendicular distance

and

angle