Menke W. Geophysical Data Analysis: Discrete Inverse Theory

Подождите немного. Документ загружается.

158

Nonlinear Inverse Problems

anywhere with equal probability. This is an adequate definition of the

null distribution. On the other hand, if the position of the object is

specified by the spherical coordinates x

[r,

+IT,

then the statement

constant actually implies that the object is near the origin. The

statement that the object could be anywhere is PN(x)

sin

The

null distribution must be chosen with the physical significance of the

vector

in mind.

Unfortunately, it is sometimes difficult to find

guiding principle

with which to choose the null distribution. Consider the case of an

acoustics problem in which a model parameter is the acoustic velocity

At first sight it may seem that a reasonable choice for the null

distribution is

PN(

constant. Acousticians, however, often work

with the acoustic slowness

I/v,

and the distribution

PN(u)

con-

stant implies

PN(

s2.

This is somewhat unsatisfactory, since one

could, with equal plausibility, argue that

PN(s)

constant,

which

case

PN(v)

v2.

One possible solution to this dilemma is to choose a

null solution whose

form

is invariant under the reparameterization.

The distribution that works in this case is

PN(v)

I/v,

since this leads

Once one has defined the null solution one can compare any other

distribution to it to measure the information content of that distribu-

tion. One commonly used quantitative measure of the information in

a distribution

is the scalar information

defined by

PN(s)

l/s.

I(P,

PN)

P(x)

log[P(x)/PN(x)l

(9.18)

The information

has the following properties [Ref.

191:

(I)

the

information of the null distribution is zero;

(2)

all distributions except

the null distribution have positive information;

(3)

the more sharply

peaked P(x> becomes, the more its information increases; and

(4)

the

information is invariant under reparameterizations. We can therefore

measure the amount of information added to the inverse problem by

imposing a priori constraints.

solve the inverse problem we must combine the a priori distribu-

tion with a distribution that represents the (possibly erroneous) theory.

We shall call this composite distribution

P’(x).

In the Gaussian case we

performed this combination simply by multiplying the distributions.

In the general case we shall find that the process of combining two

distributions

more complicated. Suppose we let

C(P,,

P2)

mean that distributions

and

are combined into distribution

9.6

Non-Gaussian Distributions

159

Then, clearly, the process of combining must have the following

properties [adapted from Ref.

191:

(a)

C(P,

P2)

should be invariant under reparameterizations.

(b) C(P,

P2)

should be commutative:

C(P,,

P2)

C(P2,

PI).

(c)

C(P,

P2)

should be associative:

C(P,

C(P2,

P3))

C(C(P,

PJ,

(d) Combining a distribution with the null distribution should

return the same distribution:

C(P,

PN)

PI.

(e)

C(P,

P2)

should be everywhere zero if and only if

everywhere zero.

These conditions can be shown to be satisfied by the choice [Ref.

191

c(P,

P2)

pIP2/pN

(9.19)

Note that

the null distribution is constant, one combines distribu-

tions simply by multiplying them.

The distribution for the theory

Pf(x)

gives the probability that the

theory will simultaneously predict data

and model parameters

the case of an implicit theory, this distribution may be exceedingly

difficult to state. On the other hand, if the theory

explicit (has form

f(x)

g(m)

0),

then the distribution for the theory can be

constructed from two component distributions: the distribution

P,(dlm)

for data

given model parameters

and the distribution for

the model parameters, which, since they are completely unknown, is

just the null distribution:

Pf(x)

Pg(dlm)PN(m)

(9.20)

The distribution

P,(dlm)

is sometimes called a conditional probability

distribution; it gives the probability of

given a value for

P3).

The total distribution is then

PT(X)

PA(X)P~(X)/PN(X)

P~(d,m)Pg(dIm)/P~(d)

(9.21)

where the second form can be used only in the case

explicit theories.

The joint probability of the data and model parameters is

PT(x).

are therefore free to consider this expression the answer to the inverse

problem. Alternatively, we could derive estimates from it, such as the

maximum likelihood point or mean, and call these the answer. On the

other hand, the probability

the model parameters alone might be

considered the answer, in which case we must project the distribution

Pp(m)

PT(x)

dd.

We could also derive answers in the form of

160

Nonlinear Inverse Problems

estimates drawn from this projected distribution [Ref.

191.

general,

each of these answers will be different from the others. Which one is

the best depends on one’s point of view.

9.7

Maximum Entropy Methods

Note that in the previous section we first had to postulate the form of

the various probability distributions to solve the inverse problem.

some cases there is good theoretical reason for using a particular

distribution (Gaussian, Poisson, exponential, white, etc).

other

cases the choice seems more arbitrary. We might ask whether we could

somehow determine the form of the distribution directly, rather than

having to assume it.

guiding principle is needed to accomplish this. One such principle

is the assertion that the best distributions are the ones with the most

information, as measured by the scalar information

[Ref.

171.

example, consider the underdetermined, linear problem

where

P(m)

is taken as unknown. Let us further assume that the

equation is interpreted

mean that the data are exactly equal to the

mean (expected value) of the model parameters

GE(m)

We can

then formulate the following problem for the distribution of the model

parameters:

Find the

P(m)

that maximizes

Z(P(m), P,(m))

subject to the constraints

GE(m)

and

P(m) dm

(9.22)

This approach is called the

maximum

entropy

method

because it was

first used in statistical mechanics. The problem can be solved by the

use of a combination of Lagrange multipliers and the calculus of

variations. At first sight the method may seem less arbitrary than

previously discussed methods that require the form of the distributions

to be known a priori. In fact it is no less arbitrary since the definition of

information

is by no means unique. The form of

stated in Eq.

(9.18)

forces

P(m)

to be an exponential distribution.

FACTOR

ANALYSIS

10.1

The Factor Analysis Problem

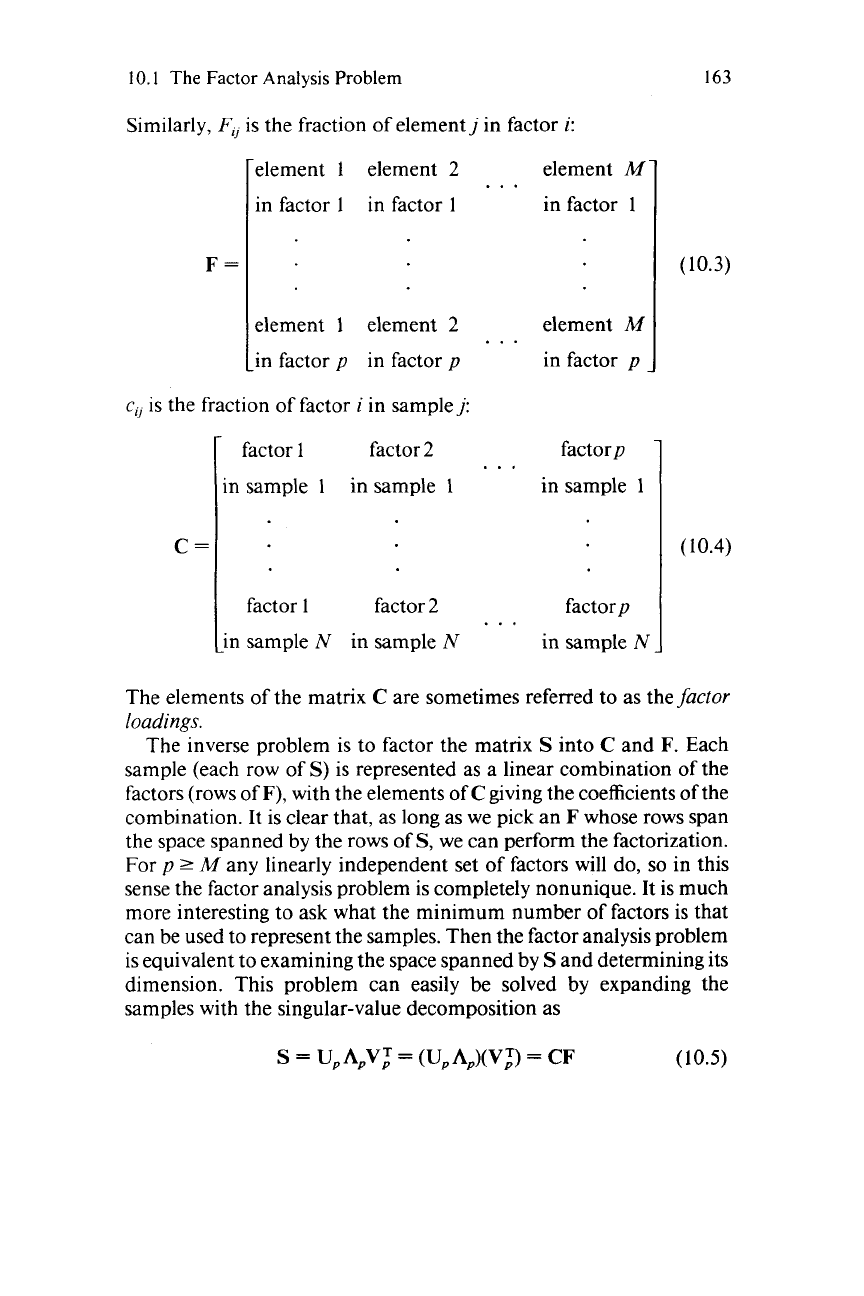
Consider an ocean whose sediment is derived from the simple

mixing of continental source rocks

and

(Fig. 10.1). Suppose that

the concentrations of three elements are determined for many samples

of sediment and then plotted on a graph whose axes are percentages of

those elements. Since all the sediments are derived from only two

source rocks, the sample compositions lie on the triangular portion of

a plane bounded by the compositions of

and

(Fig. 10.2).

The factor analysis problem is to deduce the number of the source

rocks (called

factors)

and their composition from observations of the

composition of the sediments (called

samples).

It is therefore a prob-

lem in inverse theory. We shall discuss it separately, since it provides

an interesting example of the use of some of the vector space analysis

techniques developed in Chapter

In the basic model the samples are simple mixtures (linear combina-

tions) of the factors. If there are Nsamples containing Melements and

if there are

factors, we can state this model algebraically with the

161

162

Factor

Analysis

source

element

in sample

...

(10.2)

element

in sample

...

source

ocean

sediment

Fig.

10.1.

Material from sources

and

are eroded into the ocean and mix to form

sediment. Samples

the sediment are collected and their chemical composition is

determined. The data are used to infer the composition

the sources.

equation

S=CF (10.1)

Fig.

10.2.

The composition

the sample

lies on a triangular sector

a plane

bounded

the composition

the sources

and

10.1

The

Factor

Analysis

Problem

163

Similarly,

Fl,

is the fraction of element

in factor

element

...

in factor

element

-in factor

in factor

...

ci,

is the fraction of factor

in samplej:

factor

factorp

...

factor

factorp

...

in sample

(10.3)

(10.4)

The elements of the matrix

are sometimes referred to as the

factor

loadings.

The inverse problem is to factor the matrix

into

and

Each

sample (each row of

is represented as a linear combination of the

factors (rows of

F),

with the elements of

giving the coefficients of the

combination. It is clear that, as long as we pick an

whose rows span

the space spanned by the rows of

we can perform the factorization.

For

any linearly independent set of factors will do,

in this

sense the factor analysis problem is completely nonunique. It is much

more interesting to ask what the minimum number

factors is that

can be used to represent the samples. Then the factor analysis problem

is equivalent to examining the space spanned by

and determining its

dimension. This problem can easily be solved by expanding the

samples with the singular-value decomposition as

U,A,Vg

(U,A,)(V~)

(10.5)

164

Factor

Analysis

Only the eigenvectors with nonzero singular values appear in the

decomposition. The number of factors is given by the number of

nonzero eigenvalues. One possible set of factors is the

eigenvectors.

This set of factors is not unique. Any set of factors that spans the

space will do.

we write out the above equations, we find that the composition of

the ith sample, say,

s,,

is related to the eigenvectors

and singular

values

[u,l,,~lv,

+ [Up1,2~ZV2

. .

[u,lI,~,v,

(10.6)

[Up1NI4V,

[U,IN,~,V,

* *

~up1Np3Lpvp

the singular values are arranged in descending order, then most of

each sample is composed of factor

with a smaller contribution from

factor

etc. Because

and

are vectors of unit length, on average

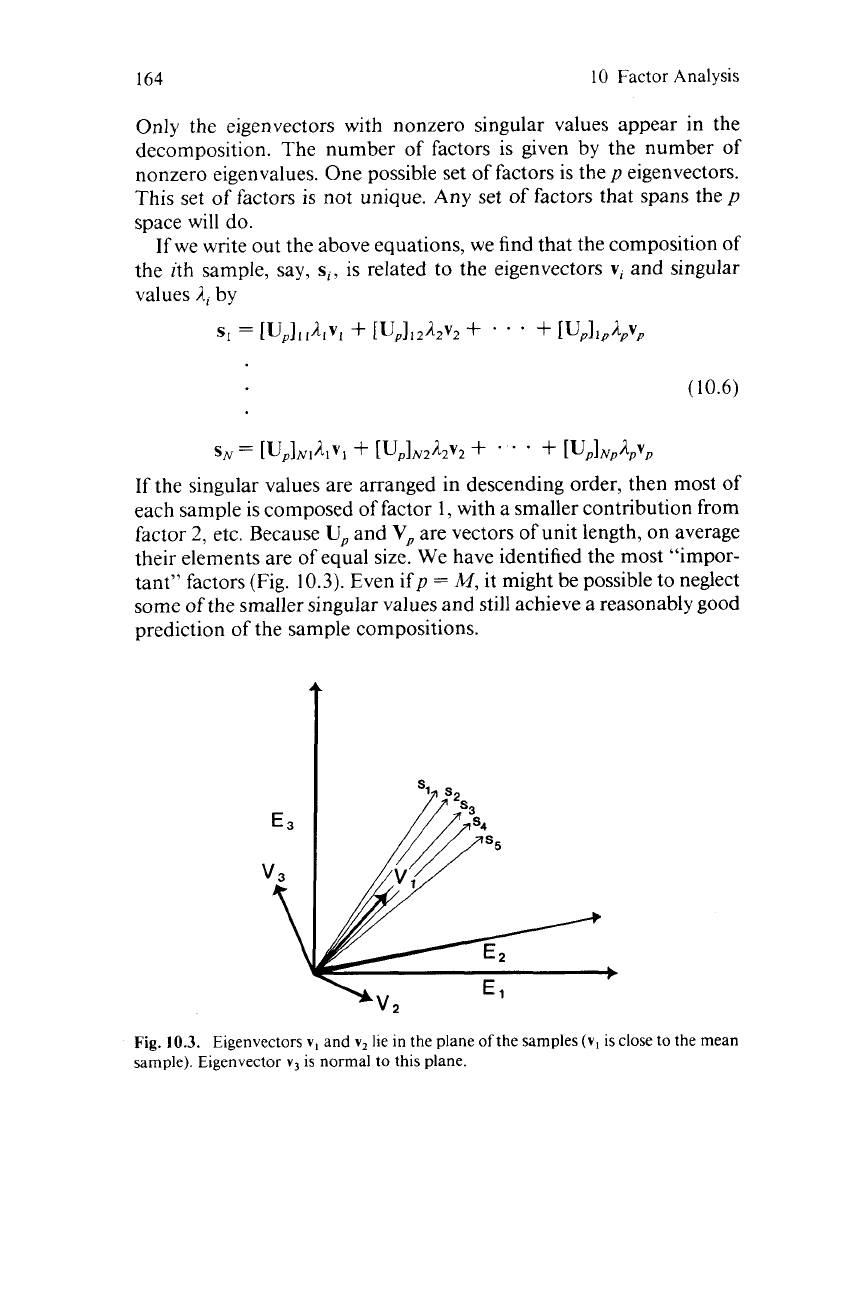
their elements are of equal size. We have identified the most “impor-

tant” factors (Fig.

10.3).

Even

ifp

it might be possible to neglect

some of the smaller singular values and still achieve a reasonably good

prediction of the sample compositions.

Fig.

10.3.

Eigenvectors

and

lie in the plane

the samples

(v,

is close to the mean

sample). Eigenvector

is normal to this plane.

10.2

Normalization and Physicality Constraints

165

The eigenvector with the largest singular value is near the mean of

the sample vectors. It is easy to show that the sample mean

(s)

maximizes the sum of dot products with the data

[s,

(s)],

while the

eigenvector with largest singular value maximizes the sum of squared

dot products

[s,

v]’.

(To show this, maximize the given functions

using Lagrange multipliers, with the constraint that

(s)

and

are unit

vectors.)

long as most of the samples are in the same quadrant, these

two functions have roughly the same maximum.

10.2

Normalization and

Physicality Constraints

In many instances an element can be important even though it

occurs only in trace quantities. In such cases one cannot neglect factors

simply because they have small singular values. They may contain an

important amount of the trace elements. It is therefore appropriate to

normalize the matrix

that there is a direct correspondence

between singular value size and importance. This is usually done by

defining a diagonal matrix of weights

(usually proportional to the

reciprocal of the standard deviations of measurement of each of the

elements) and then forming a new weighted sample matrix

S’

SW.

The singular-value decomposition enables one to determine a set of

factors that span,

approximately span, the space of samples. These

factors, however, are not unique in the sense that one can form linear

combinations of factors that also span the space. This transformation

is typically a useful thing to

since, ordinarily, the singular-value

decomposition eigenvectors violate a priori constraints on what

“good” factors should be like. One such constraint is that the factors

should have a unit

norm, that is, their elements should sum to one.

If the components of a factor represent fractions of chemical elements,

for example, it is reasonable that the elements should sum to

100%.

Another constraint is that the elements of both the factors and the

factor loadings should be nonnegative. Ordinarily

material is com-

posed of a positive combination of components. Given an initial

representation of the samples

CFW-’,

we could imagine finding a

new representation consisting of linear combinations of the old fac-

tors, defined by

F’

TF,

where

is an arbitraryp

transformation

matrix. The problem can then be stated.

166

Factor Analysis

Find

subject to the following constraints:

[F'W-'IiJ

for all

(10.7)

[CT'],

for all

andj

[F'W-I],

for all

andj

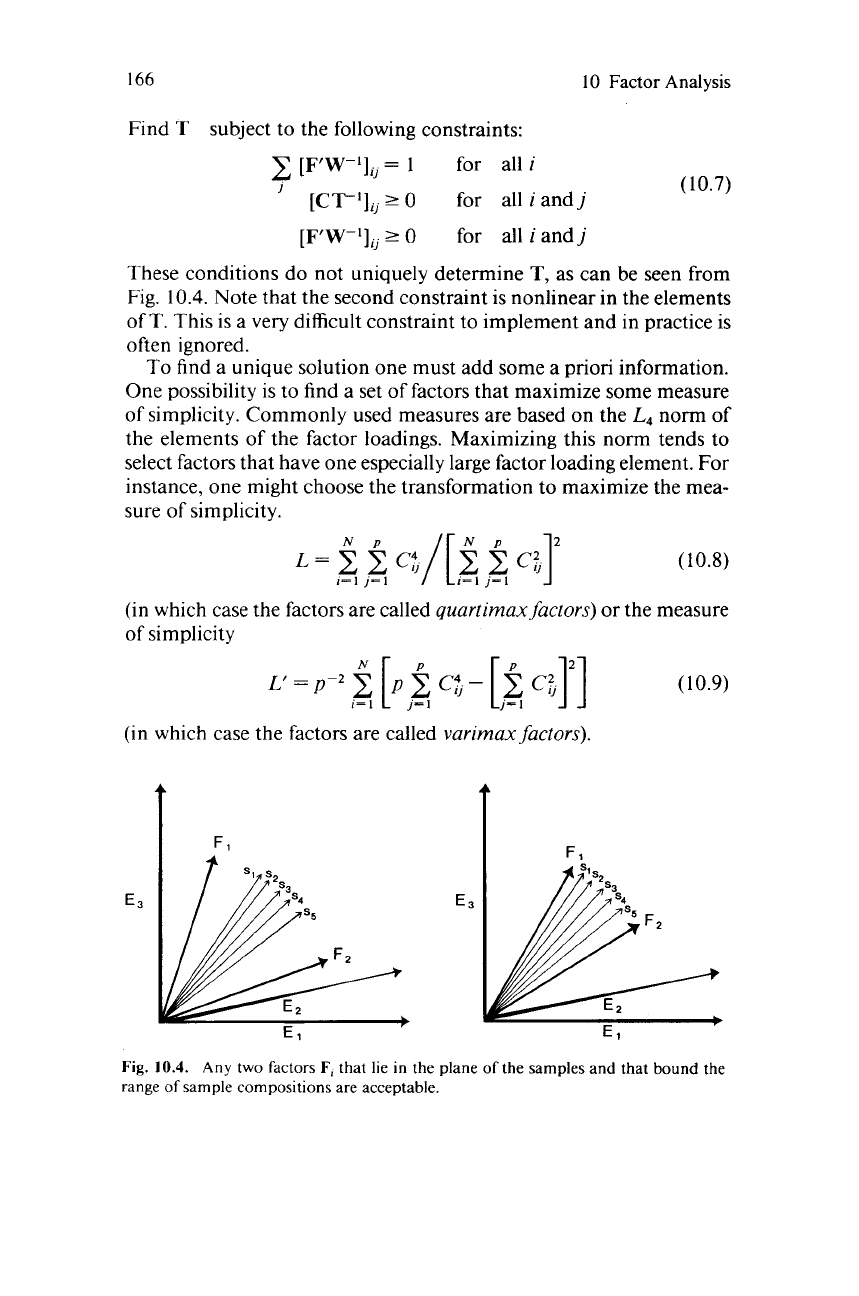
These conditions do not uniquely determine

T, as can be seen from

Fig. 10.4. Note that the second constraint is nonlinear in the elements

This is a very difficult constraint to implement and in practice is

often ignored.

To find a unique solution one must add some a priori information.

One possibility is to find a set of factors that maximize some measure

of simplicity. Commonly used measures are based on the

norm of

the elements of the factor loadings. Maximizing this norm tends to

select factors that have one especially large factor loading element. For

instance, one might choose the transformation to maximize the mea-

sure of simplicity.

(10.8)

(in

which case the factors are called

quartimaxfactors)

or the measure

simplicity

(10.9)

(in which case the factors are called

varimax factors).

Fig.

10.4.

Any two factors

that lie in the plane of the samples and that bound the

range

sample compositions are acceptable.

10.4

Empirical Orthogonal Function Analysis

167

Another possible way of adding a priori information is to find

factors that are in some sense close to a set of a priori factors. If

closeness is measured by the

norm and if the constraint on the

positivity of the factor loadings is omitted, then this problem can

solved using the techniques of Chapters

and 12. One advantage of

this latter approach is that it permits one to test whether a particular set

of a priori factors can be factors of the problem (that is, whether or not

the distance between

priori factors and actual factors can be reduced

to an insignificant amount).

10.3

@Mode and R-Mode Factor Analysis

In addition to the normalization of the sample matrix

described

above (which is based on precision of measurement), several other

kinds of normalizations are commonly employed. One, given the

name

mode,

is used to counter the common problem that measured

data do not always have a unit

norm because some of their

components are not included in the analysis. The individual samples

are therefore normalized before any calculations are made, which has

the effect of making the factors dependent on only the ratios of the

observed elements. They are usually normalized to unit

norm,

however; the eigenvectors of the singular-value decomposition then

have the physical interpretation of extremizing the sum of squared

cosines of

angles

between the samples, instead of just extremizing the

dot products (see Section 10.1).

Another type of normalization is used when the data possess only

small variability. It is then appropriate to remove the mean sample

from the data before performing the factor analysis

that perturba-

tions about the mean sample are directly analyzed. When this kind of

normalization is applied, the name

R-mode

analysis

is used.

10.4

Empirical Orthogonal

Function Analysis

Factor analysis need not be limited to data that contain actual

mixtures

components. Given any set of vectors

si,

one can perform

the singular-value decomposition and represent

as a linear combina-