Menke W. Geophysical Data Analysis: Discrete Inverse Theory
Подождите немного. Документ загружается.

148
9
Nonlinear Inverse Problems
<”
1)
parameter
X
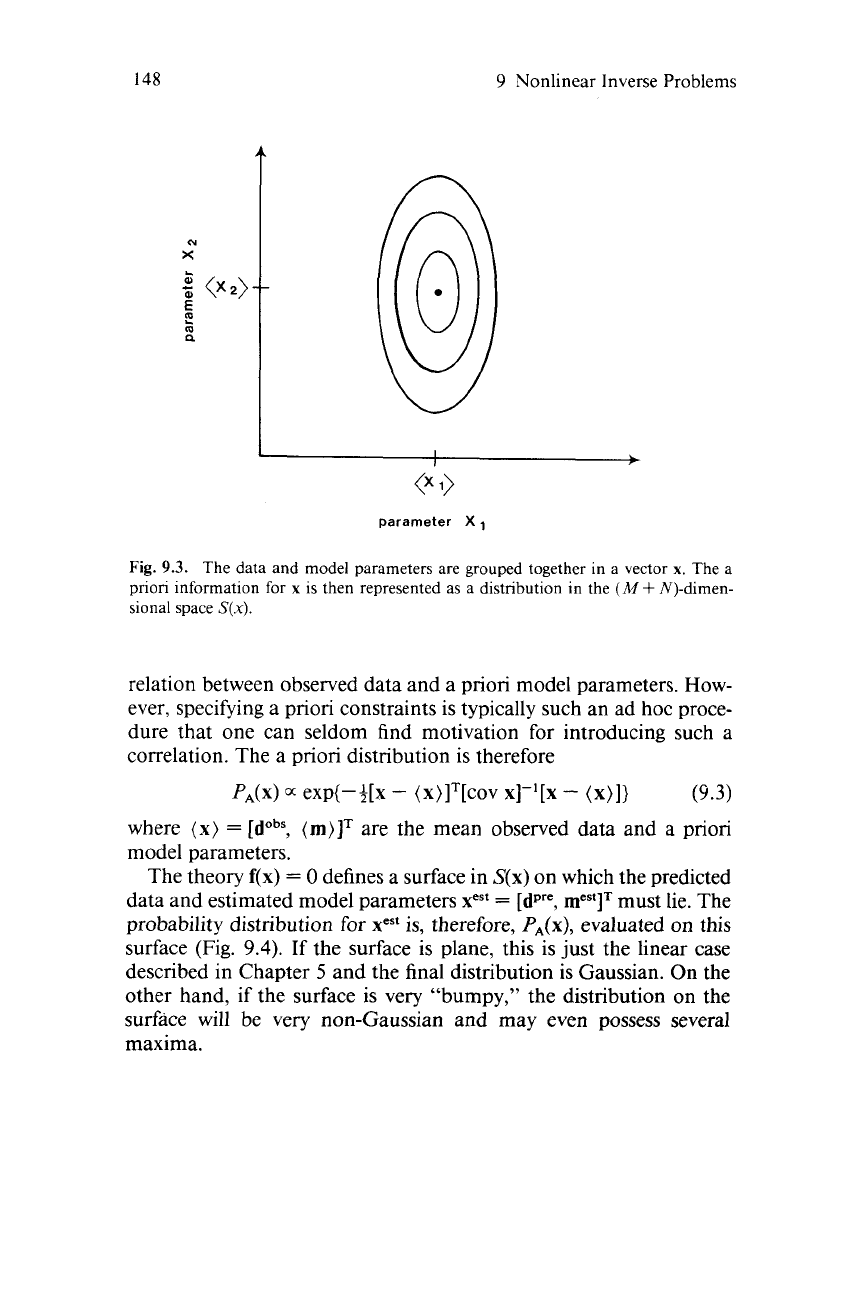
Fig.
9.3.
The data and model parameters are grouped together in a vector
x.
The a
priori
information
for
x
is then represented as a distribution in the
(M
+
N)-dimen-
sional space
S(x).
relation between observed data and a priori model parameters. How-
ever, specifying a priori constraints is typically such an ad hoc proce-
dure that one can seldom find motivation for introducing such a
correlation. The a priori distribution is therefore
PA(x)
exp(-$[x
-
(x)lT[cov x]-’[x
-
(x)])
(9.3)
where
(x)
=
[dabs,
(m)lT are the mean observed data and a priori
model parameters.
The theory
f(x)
=
0
defines a surface in S(x) on which the predicted
data and estimated model parameters xest
=
[dpre,
mest]= must lie. The
probability distribution for xest is, therefore, PA(x), evaluated on this
surface (Fig.
9.4).
If the surface is plane, this is just the linear case
described in Chapter
5
and the final distribution is Gaussian. On the
other hand, if the surface is very “bumpy,” the distribution on the
surface will be very non-Gaussian and may even
possess
several
maxima.
9.3
The Nonlinear Inverse Problem with
Gaussian
Data
149
Xest
1
parameter
X,
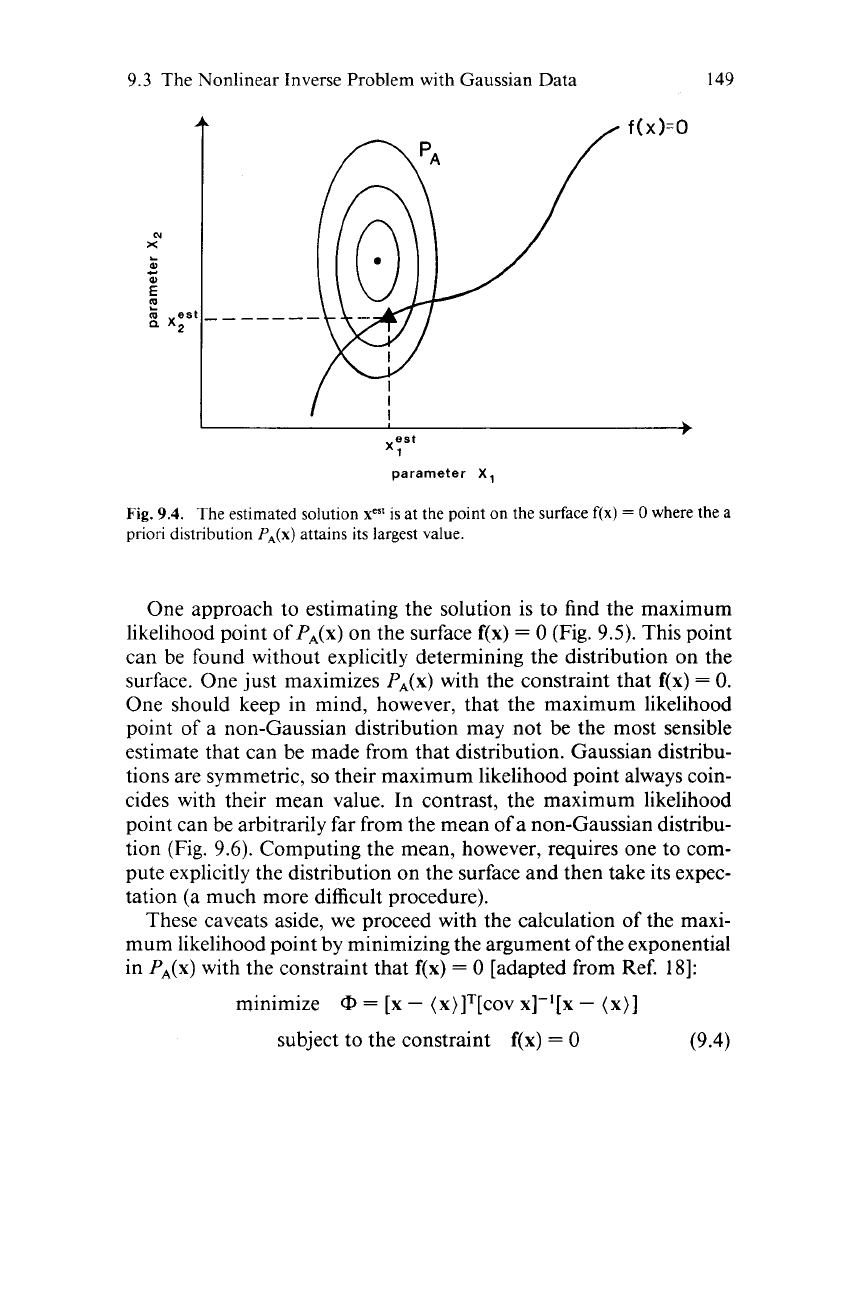
Fig.
9.4.
The estimated solution
xcsr
is at the point on the surface
f(x)
=
0
where the
a
priori
distribution
P,(x)
attains its largest value.
One approach to estimating the solution is to find the maximum
likelihood point of PA(x) on the surface
f(x)
=
0
(Fig.
9.5).
This point
can be found without explicitly determining the distribution on the
surface. One just maximizes PA(x) with the constraint that
f(x)
=
0.
One should keep in mind, however, that the maximum likelihood
point of a non-Gaussian distribution may not be the most sensible
estimate that can be made from that distribution. Gaussian distribu-
tions are symmetric,
so
their maximum likelihood point always coin-
cides with their mean value. In contrast, the maximum likelihood
point can be arbitrarily far from the mean
of
a non-Gaussian distribu-
tion (Fig.
9.6).
Computing the mean, however, requires one to com-
pute explicitly the distribution on the surface and then take its expec-
tation (a much more difficult procedure).
These caveats aside, we proceed with the calculation of the maxi-
mum likelihood point by minimizing the argument of the exponential
in PA(x) with the constraint that
f(x)
=
0
[adapted from Ref.
181:
minimize
CD
=
[x
-
(x)IT[cov
x]-'[x
-
(x)]
subject to the constraint
f(x)
=
0
(9.4)
150
9
Nonlinear Inverse Problems
S
S
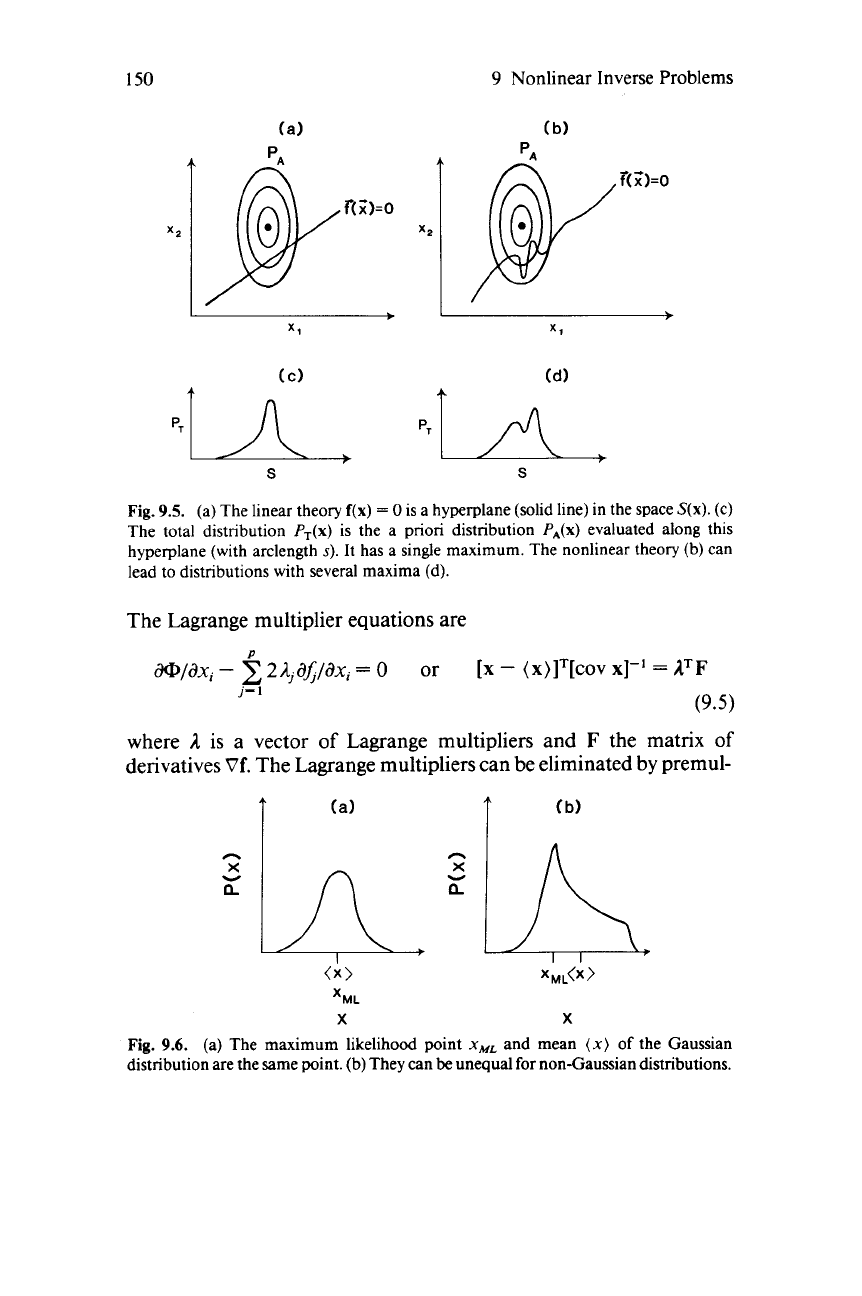
Fig.
9.5.
(a) The linear theory
f(x)
=
0
is a hyperplane (solid line) in the space
S(x).
(c)
The total distribution
PT(x)
is the a pnon distribution
P,(x)
evaluated along this
hyperplane (with arclength
3).
It has a single maximum. The nonlinear theory (b) can
lead to distributions with several maxima (d).
The Lagrange multiplier equations are
P
m/axi
-
2)LjdQaxi
=
0
or [x
-
(x)lT[cov
XI-’
=
ATF
j-
I
(9.5)
where
1
is a vector
of
Lagrange multipliers and
F
the matrix
of
derivatives
Vf.
The Lagrange multipliers can be eliminated
by
premul-
n
X
W
n
(a)
n
<x>
‘ML
X
X
Fig.
9.6.
(a) The maximum likelihood point
xML
and mean
(x)
of the Gaussian
distribution are the same point. (b) They can
be
unequal for nonaaussian distributions.

9.3
The Nonlinear Inverse Problem with Gaussian Data
151
tiplying the transformed Lagrange equation by
F
as
F[x
-
(x)]
=
F[COV x]FTA
1
=
(F[COV
x]FT}-'F[x
-
(x)]
(9.6)
(9.7)
and then premultiplying by (F[cov x]FT)-' as
Substitution into the original equation yields
[X
-
(x)]
=
[COV x]F~{F[cov x]FT}-'F[x
-
(x)]
(9.8)
which must be solved simultaneously with the constraint equation
f(x)
=
0.
These two equations are equivalent to the single equation
[X
-
(x)]
=
[COV x]F~(F[cov x]FT}-'(F[x
-
(x)]
-
f(x))
(9.9)
since the original two equations can be recovered by premultiplying
this equation by F. Since the unknown
x
appears on both sides of the
equation and since
f
and
F
are functions
of
x,
this equation may be
difficult to solve explicitly. Only in the linear case when f(x)
=
Fx
(F being constant) is its solution comparatively simple, as was shown
in Chapter
5.
We now examine an iterative method of solving it. This
method consists of starting with some initial guess, say,
x?'
where
n
=
0,
and then generating successive approximations as
x%;"+l
=
(x)
+
[COV x]F;~(F,[cov x]F;~)-'(F~[xY
-
(x)]
-
f(x?))
(9.10)
The subscript on F, implies that it is evaluated at
x?'.
If the initial guess
is close enough to the maximum likelihood point, the successive
approximations will converge to the desired value. We shall discuss the
matter of convergence in more detail.
If
the theory is explicit (i.e.,
if
f(x)
=
d
-
g(m)
=
0)
and if the data
and a priori model parameters are uncorrelated, the iterative formula
can be rewritten as
m?:,
=
(m)
+
G;g(d
-
g(rnYt)
+
Gn[myt
-
(m)])
G;g
=
[cov m]G;f([cov d]
+
G,[cov m]G;f}-'
(9.11)
=
([cov
m]-'
+
G;f[cov d]-'G;}-'G;f[cov a]-'
where [G,];,
=
dgi/dmj
is evaluted at
my'
and where the generalized
inverse notation has been used for convenience. These formulas are
the nonlinear, iterative analogues to the linear, noniterative formulas

152
9
Nonlinear Inverse Problems
stated for the linear inverse problem in Section
5.7,
except that in this
case the theory has been assumed to be exact. If the theory is inexact
with a Gaussian distribution
of error
Pg(mld)
described by covariance
[cov
g]
(see Section
5.9,
then one must find the maximum likelihood
point of the total distribution
PT(x)
=
P,(x)P,(mld),
as was done in
Section
5.6
for the linear case. The formulas one obtains are just the
iterative formulas stated above with each occurrence of [cov
d]
re-
placed by [cov d]
+
[cov
g].
Since the distribution for
mest
is non-Gaussian, its covariance is both
difficult to calculate and difficult to interpret in terms of confidence
intervals.
If
the problem is not too nonlinear, the covariance might be
estimated using the linear formula
[cov
mest]
=
G;g[cov
d]G;gT
+
[I
-
R,][cov
m][I
-
R,JT
(9.12)
where
R,
=
G;G,
and the last
n
in the iteration is used. The same
restriction applies to interpretations of the resolution matrices
N
and
R. Since the problem is nonlinear, they do not describe the true
resolution of the problem. On the other hand, they give the resolution
of
a linear problem that is in some sense close to the nonliner one.
The iterative formulas for
mest
can also be derived from a somewhat
different point
of
view. The nonlinear equation
g(m)=d
can be
linearized by expanding it about some point, say,
myt
using Taylor's
theorem as
g(m)
--
g(myt)
+
Vg[m
-
myt]
=
g(mFt)
+
G,[m
-
my']
(9.13)
where we have ignored terms of second order and higher. Defining
Am,,,
=
[m
-
my'],
we can write the approximate equations as
G,
Am,+
=
d
-
g(myt)
my?,
=
myt
+
Am,,,
(9.14)
If
one makes an initial guess
of
wt,
the first equation can be solved
for
Aml
by any of the methods of Chapters
3
-
5,
and a new guess
mpst
can
be computed from the second equation. The process can be iterated
until a solution to the inverse problem is obtained. Note, however, that
measures of solution length should be based on the length
of
my?
,,
not
just on the length of the perturbation
Amn+
,
. The application to this
problem of the linear formulas derived in Section
5.7
leads to exactly
the nonlinear iterative equation derived in Eq.
(9.1
1).

9.5
L,
Convergence and Nonuniqueness
153
9.4
Special Cases
9.4.1 LEAST SQUARES SOLUTIOh
We
assume that the data are independent, that they have uniform
variance
~72,
and that no a priori information has been added to the
problem:
=
[GTG,]-'G;S[d
-
g(my')]
+
myt
(9.15)
9.4.2 DAMPED LEAST SQUARES
with zero mean and uniform variance
a;:
We assume that the a priori model parameters are independent
my:'
=
GTG,
+
+I
GT[d
-
g(rnyt)]
+
myt
(9.16)
[
::
I-'
9.4.3 MINIMUM-LENGTH SOLUTION
We assume that the a priori model parameters are independent with
my:,":l
=
GW[G,GT]-'[d
-
g(my')]
+
myt
(9.17)
Note that, in the minimum-length case, the perturbation
Am
is
minimized (as ism). This is a mathematical coincidence and is not true
for other choices of [cov
m].
infinite variance and zero mean:
9.5
Convergence and Nonuniqueness
of
Nonlinear
L,
Problems
In the linear case we found simple means for deciding whether a
problem has a unique solution. In contrast, there are no simple means
for deciding whether a nonlinear inverse problem has a unique solu-
tion that minimizes prediction error in the absence
of
a priori infor-
mation. Consider the very simple nonlinear model
d,
=
m:
+
m,m,z,.
This problem can be linearized by the transformation of variables
mi
=
rn:,
m;
=
rn1m2
and can therefore be solved by the least squares
method if
N>
2.
Nevertheless, even if the primed parameters are

154
9
Nonlinear Inverse Problems
,,,est
model parameter m
Fig.
9.7.
Error
E
for
the
linear Gaussian case
is
always
a
paraboloid.
unique, the unprimed ones are not: if
mest
is a solution that minimizes
the prediction error, then
-
mest
is also a solution with the same error.
In this instance the error
E(m)
has two minima of equal depth.
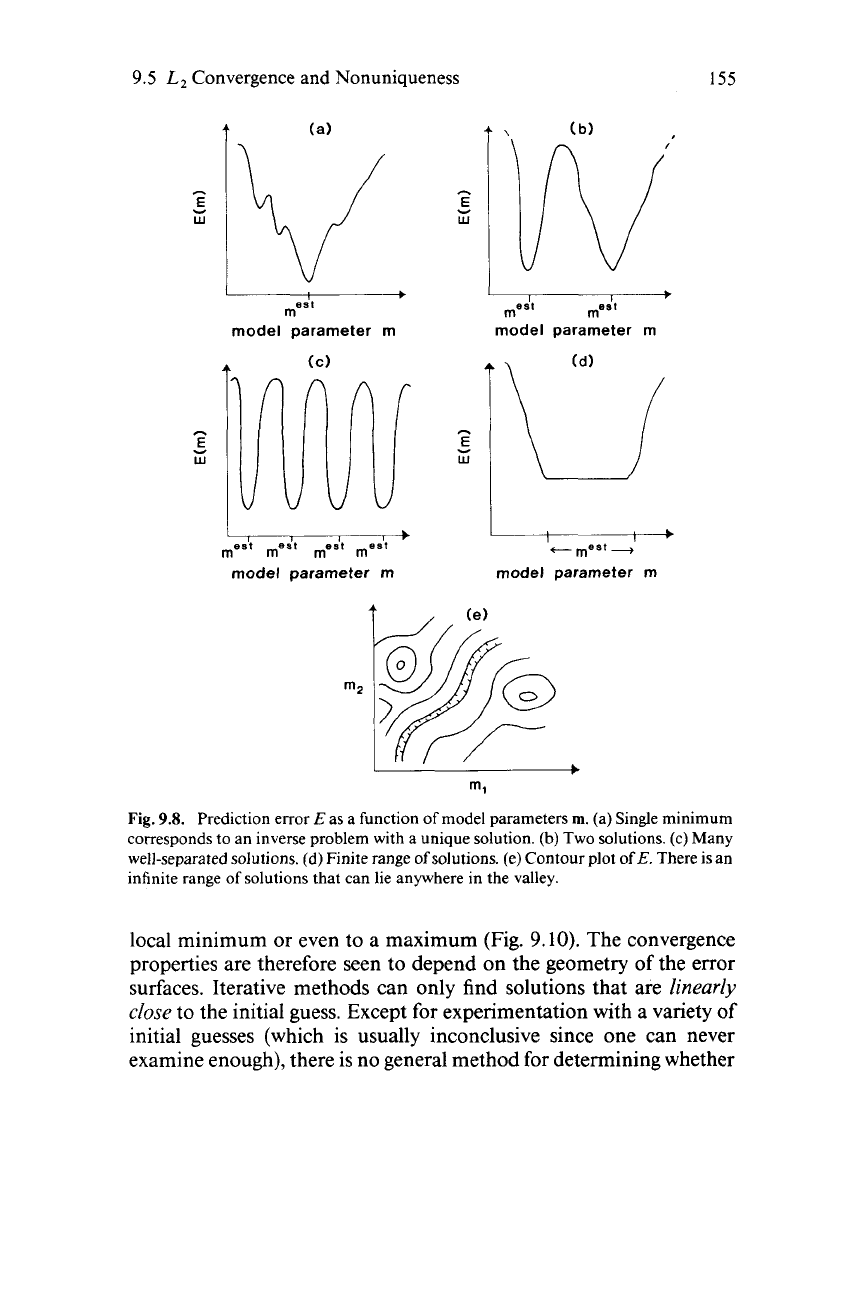
To investigate the question of nonuniqueness, we must examine the
global properties of the prediction error. If the surface has but a single
minimum point, then the solution is unique. If it has more than one
minimum point, the solution is nonunique, and a priori information
must be added to resolve the indeterminacy. The error surface of a
linear problem is always a paraboloid (Fig.
9.7),
which can have only a
simple range of shapes. An arbitrarily complex nonlinear inverse
problem can have an arbitrarily complicated error. If
A4
=
2
or
3,
it
may be possible to investigate the shape of the surface by graphical
techniques. For most realistic problems this is infeasible [Fig.
9.81.
Even if an inverse problem is known to have a unique solution, there
is no guarantee that the iterative technique described above will
converge to the solution. The difficulty arises from the fact that the
linearized method does not “see” the entire error surface
E(m).
In-
stead, it sees only the part of
E(m)
in the vicinity of
myt
and approxi-
mates the rest of the surface as a paraboloid tangent to the actual
surface at that point. The new estimate
m;:,
is the minimum
of
the
paraboloid (Fig.
9.9).
Since any minimum with continuous derivatives
is locally paraboloid in shape, the method will converge to the mini-
mum of the error function if the initial guess is close enough. If it is not
close enough, the process may not converge at all or may converge to a
9.5
L,
Convergence and Nonuniqueness
155
mest
model parameter
m
u
mest
mest
model parameter m
t
mest
me
s
t
model parameter
m
t
m-t
+
model parameter m
m1
Fig.
9.8.
Prediction error
E
as a function of model parameters
rn.
(a) Single minimum
corresponds to an inverse problem with a unique solution. (b) Two solutions. (c) Many
well-separated
solutions.
(d) Finite
range
of solutions. (e) Contour plot ofE. There is an
infinite range
of
solutions that can lie anywhere in the valley.
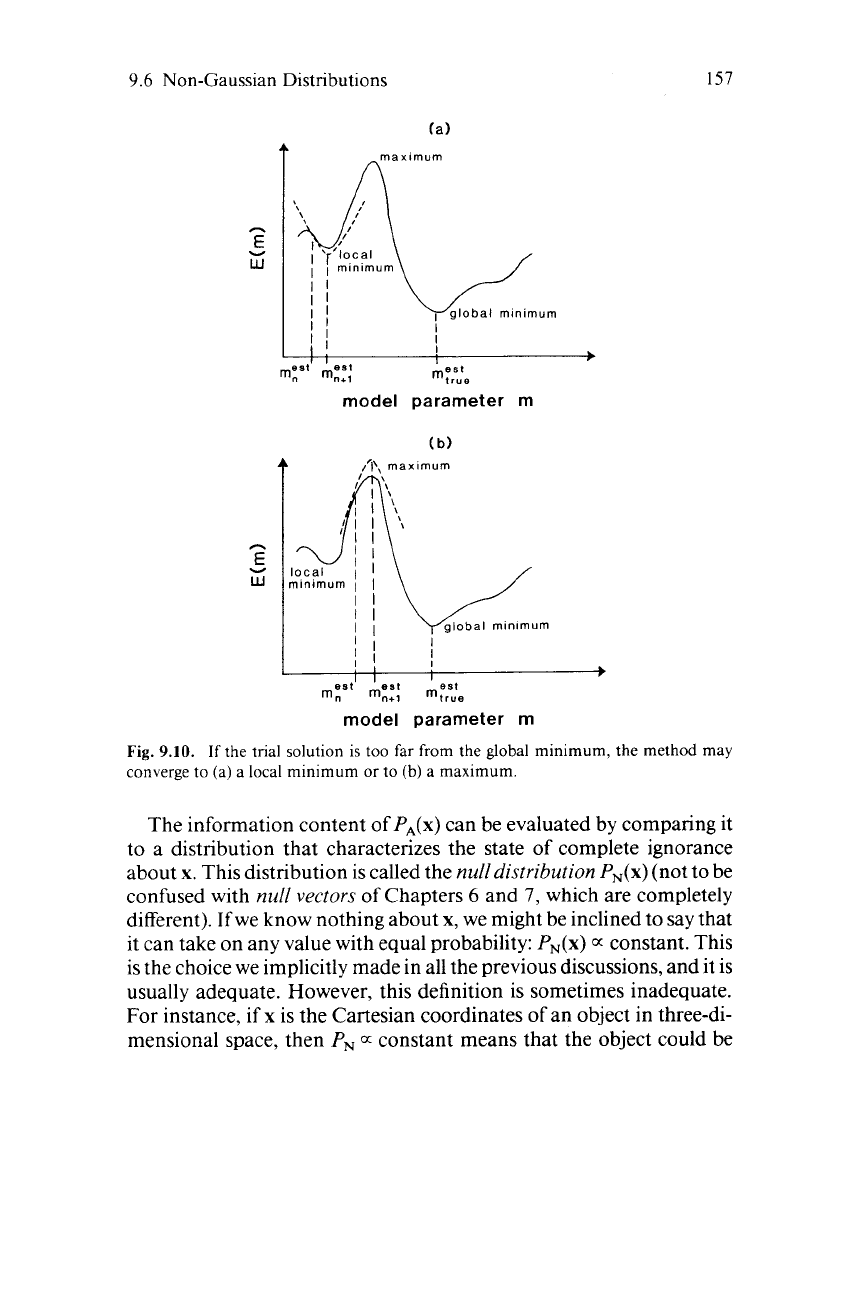
local minimum or even to a maximum (Fig.
9.10).
The convergence
properties are therefore seen to depend on the geometry
of
the error
surfaces. Iterative methods can only find solutions that are
linearly
close
to the initial guess. Except for experimentation with a variety
of
initial guesses (which is usually inconclusive since one can never
examine enough), there is no general method
for
determining whether

156
9
Nonlinear
Inverse
Problems
I
I
I
I
Fig.
9.9.
The iterative method locates the global minimum
of
the error E(solid curve)
by locating the minimum
of
the paraboloid (dashed curve) that is tangent
to
Eat
the
trial solution
m:'.
a solution obtained by the iterative method really does minimize error
in the global sense.
9.6
Non-Gaussian Distributions
In Section
5.7
the general distribution of model parameters and data
for a linear, Gaussian theory was derived. In Section
9.2
this analysis
was extended to nonlinear, Gaussian theories. In both cases the answer
to the inverse problem was based on a distribution -either the pro-
jected distribution for the model parameters or some estimate com-
puted from that distribution.
To
extend this analysis to the completely general case requires a
more careful analysis of the way in which the component probability
distributions are defined and combined [Ref.
191.
We shall begin, as
we did in the other cases, by assuming that we can define an a priori
distribution
PA(d,
m)
=
PA(x)
for observed data and a priori model
parameters. We use this distribution to characterize all that is known
about model parameters and data before applying the actual theory.
157
9.6
Non-Gaussian Distributions
model parameter m
Ii
I
I
I
mest'
mest
-b
n
n+l
true
model parameter
rn
Fig.
9.10.
If
the trial solution is too far from the global minimum, the method may
converge to (a) a local minimum
or
to (b) a maximum.
The information content of
P,(x)
can be evaluated by comparing it
to a distribution that charactenzes the state of complete ignorance
about
x.
This distribution is called the
null
distribution
PN(x)
(not to be
confused with
null
vectors
of Chapters
6
and
7,
which are completely
different).
If
we know nothing about
x,
we might be inclined to say that
it can take on any value with equal probability:
PN(x)
c~
constant. This
is the choice we implicitly made in all the previous discussions, and it is
usually adequate. However, this definition is sometimes inadequate.
For instance, if
x
is the Cartesian coordinates of an object in three-di-
mensional space, then
PN
0~
constant means that the object could be
