Mench M.M. Fuel Cell Engines

Подождите немного. Документ загружается.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

240 Transport in Fuel Cell Systems

0.1

1.0

10 100

0.1

1.0

Flow direction

Superficial gas velocity, V

(ft/s)

Superficial water velocity, V

(ft/s)

Annular mist

(water

dispersed)

Bubble

(Air dispersed)

Slug 4

(Air dispersed)

Froth

(Both phases

dispersed)

Figure 5.22 Various ﬂow regimes: (a) bubble ﬂow; (b) slug; (c) froth; (d) annular mist. (Adapted

from Ref. [34].)

cathode ﬂow channels and porous media, depending on operating conditions. In general,

multiphase mixtures can be characterized by several different ﬂow regimes, based on the

characteristics of the two-phase ﬂow, as illustrated in Figure 5.22. The ﬂow regime transition

regions are not discrete, and the discernment between different ﬂow regimes is somewhat

subjective. Additional subregimes beyond those shown have also been deﬁned for different

situations.

The phases are classiﬁed according to the superﬁcial gas and liquid velocity. The

superﬁcial gas-phase velocity can be written as

channel

(5.83)

where Q

is the volume ﬂow rate of gas in the channel and A

channel

is the cross-sectional

area of the channel. Thus, the superﬁcial gas-phase velocity represents the velocity the

gas phase would have if it occupied the channel as a single phase. The superﬁcial liquid

velocity is deﬁned similarly:

channel

(5.84)

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.5 Multiphase Mass Transport in Channels and Porous Media 241

Flow velocity

Diffusion media

Figure 5.23 Image of liquid droplet in ﬂow channel under shear.

At low superﬁcial gas velocities, ﬂow is in the bubble regime, because of the low volume

of the gas phase. This regime is appropriate for liquid reactant solutions with gas-phase

products of reaction, as occurs in the DMFC anode covered in Chapter 6. As the gas-

phase velocity increases, the viscous drag on the liquid phase increases, and a transition is

made into a slug regime, which is represented by coalesced droplets of liquid that are

charaterised by nonuniform, irregular motions. The droplet in Figure 5.23 is shown under

drag in a ﬂow channel in the slug ﬂow regime [35].

Beyond the slug regime, as the liquid droplets become more sparse and the gas-phase

velocity increases, the ﬂow transitions into a froth regime, characterized by high turbulence

and a general pattern of liquid slugs and mist ﬂow. As the gas-phase ﬂow rate is further

increased, the high drag on the droplets in the ﬂow channel create an annular mist ﬂow,

where some liquid will form as a coalesced ﬁlm on channel walls and as a ﬁne mist of

droplets in the gas ﬂow stream. A neutron image of a 50-cm

fuel cell ﬂow ﬁeld that shows

some annular and slug behavior is shown in Figure 5.24.

The channel wall shape and surface properties also have an important effect. Annular

ﬁlms will not tend to form on hydrophobic surfaces or along surfaces with sharp angles,

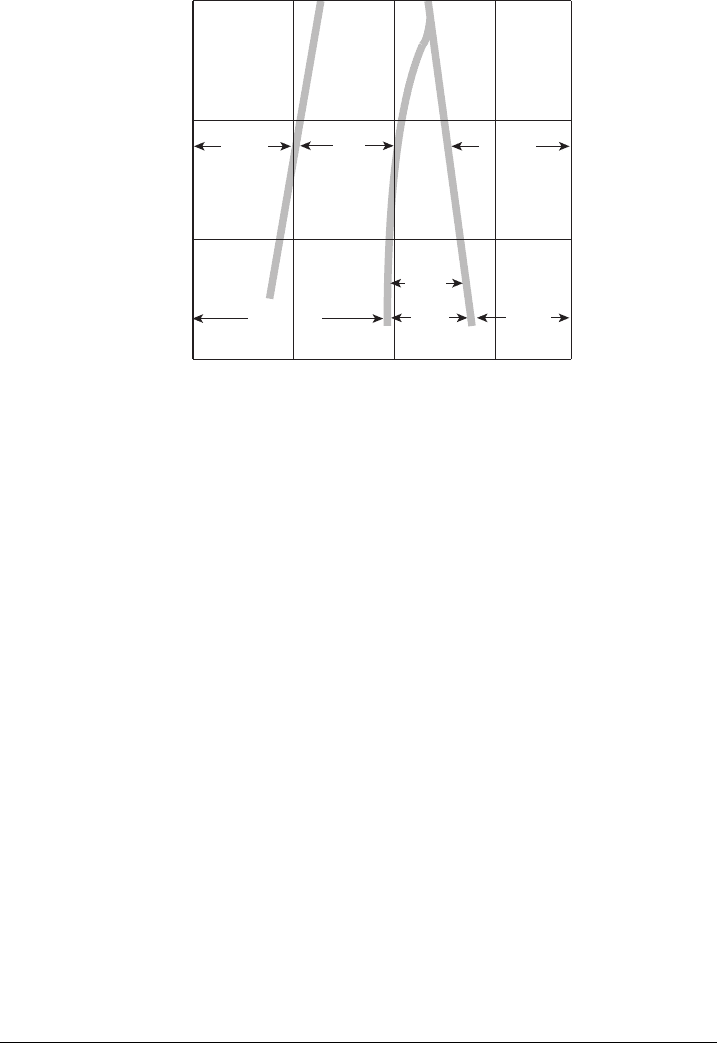
such as the triangular shape. A photograph of liquid water droplets along the surface

of a triangular and rounded channel is shown in Figure 5.25. In operation, the presence

of an annular ﬁlm is difﬁcult to remove but results in a more evenly balanced pressure

distribution by absorbing slugs, thus helping prevent misdistribution of ﬂow in stacks.

For slugs in channels, shear force dominates the removal [35]. The shear force is directly

related to the channel velocity, so that droplet purge can be accomplished with short bursts

of increased channel ﬂow velocity. Because the superﬁcial liquid velocity is so low in most

PEFCs, the ﬂow regime most characteristic is the annular mist regime, although at low

gas-phase velocity conditions, such as occur in the anode under low power, a slug regime

can be normal. The pressure drop in the slug regime can be sporadic, which can have

important consequences on the ﬂow distribution in the stack plates or individual channels.

Speciﬁcally, if the pressure drop in one plate is much higher than others, the ﬂow from the

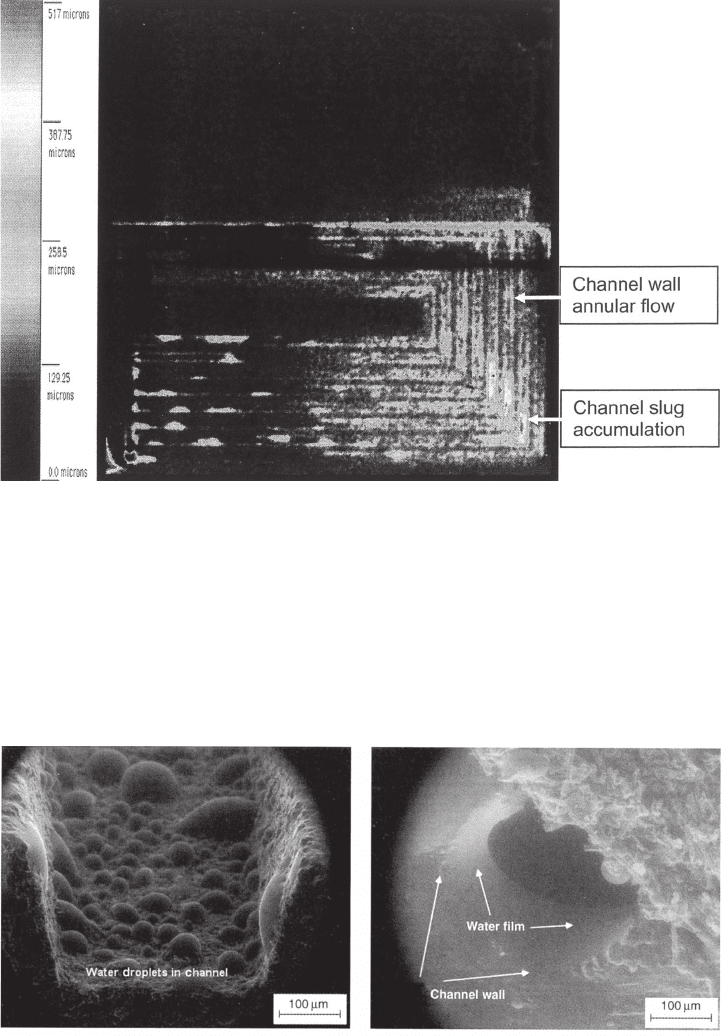
c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

242 Transport in Fuel Cell Systems

Figure 5.24 Neutron Image of ﬂow in PEFC showing some partial slug and annular ﬂow behavior

along channel walls [37].

manifold can be redirected to nonﬂooded fuel cells and result in a starved fuel cell plate

and possible voltage reversal if ﬂooding occurs.

Because the various ﬂow regimes are quite complex, a generally uniﬁed treatment of

the ﬂow patterns does not exist, and the background knowledge is taken from experimental

studies of oil–air, oil–water, or water–oil ﬂow in much larger pipes than the relatively

Figure 5.25 Image of liquid water inside a fuel cell ﬂow channel with triangular and rounded

surfaces. (From Ref. [32] with permission.)

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.5 Multiphase Mass Transport in Channels and Porous Media 243

Superficial liquid velocity, V

, ft/sec

Superficial gas velocity, V

, ft/sec

1.0

0.1

0.01

100

1.00.1 500

Bubble

Slug

Froth

Annular

Mist

Light Phase

Disersed

Heavy

Phase

Dispersed

Phase

Mixed

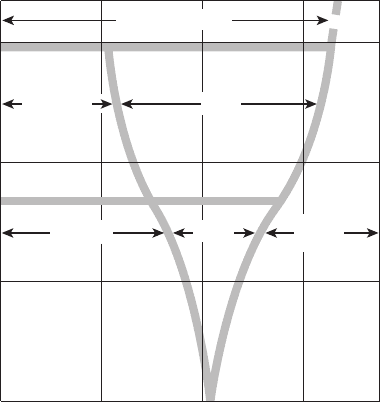
Figure 5.26 Generalized ﬂow regime map for vertical pipes. (Adapted from [34].)

small channels used in most fuel cells. Thus, some ambiguity exists, although microﬂuidic

study is rapidly advancing for geometries more appropriate for fuel cells. Gravity effects

do play an important role in the transition between different regimes, and as a result the

channel orientation has an effect on the transition. Gravity effects play an important factor

in liquid water removal in the manifolds and ﬂow channels, so stock orientation is on

important design consideration. A generalized ﬂow regime chart for vertically oriented

pipes is shown in Figure 5.26. For horizontal pipes, a generalized ﬂow regime map for

air–water mixtures is given in Figure 5.27.

5.5.2 Multiphase Flow in PEFC Porous Media

Multiphase ﬂow in porous media is a very important topic for low-temperature PEFCs

because water produced at the cathode ﬂows through the porous catalyst layers and porous

gas diffusion media. Any local blockage of normally open pores restricts reactant ﬂow

to the reaction sites, a phenomenon known as ﬂooding. The water balance and ﬂooding

in a PEFC is described in detail in Chapter 6. Here, the basic fundamentals that describe

two-phase ﬂow in porous media are described to guide and understanding.

Unfortunately, the science of multiphase ﬂow though thin-ﬁlm mixed hydrophobic/

hydrophilic porous media in fuel cells, which includes the catalyst layers and diffusion

media is not yet well developed, and much of the present level of understanding is based on

This section may be omitted without loss of continuity providing detailed analysis of PEFC ﬂooding covered in

Chapter 6 is also omitted.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

244 Transport in Fuel Cell Systems

Superficial water velocity, V

(ft/s)

Superficial air velocity, V

(ft/s)

1.0

0.1

0.01

100

1.00.1 500

Elongated

bubble

Slug

Wave

Annular

mist

Stratified

Dispersed bubble

Figure 5.27 Generalized ﬂow regime map for horizontal pipes. (Adapted from [34].)

application of porous media theory from civil and petroleum engineering studies of ﬂow of

water or oil through packed soil beds. The minute length scales and complex materials in

fuel cells present many unique and challenging physicochemical issues.

There are a few key differences between the understanding from soil science and

petroleum engineering and fuel cell media which make the direct use of semiempirical

relationships derived using unconsolidated soil for consolidated porous fuel cell media

somewhat dubious:

1. The transport length scale in fuel cell media is much smaller.

2. The thin-ﬁlm media in fuel cells have a very large surface area–volume ratio, so

that interfacial effects not dealt with in bulk ﬂow theory become very important.

3. Very little treatment of vaporization/condensation is available from soil science,

which has a major impact on low-temperature fuel cells.

4. Most soil science studies have been conducted with hydrophilic media, whereas the

PEFC media typically have a highly heterogeneous surface energy distribution with

a net hydrophobic surface condition.

5. Most soil science modeling/work is done in the saturated domain (that is, the pores

of the soil are completely ﬁlled with ﬂuid). Fuel cell materials are almost always

only partially saturated.

6. The models and physics attempt to account for bulk ﬂow, but not for unconnected

orphan droplets believed to be common in fuel cell media.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.5 Multiphase Mass Transport in Channels and Porous Media 245

Flow of the liquid phase in fuel cell porous media is driven by several forces:

1. Capillary Action This is a result of a pressure difference between the phases and

dominates for small pores. Capillary forces are responsible for the motion of water

into a sponge, wax up a candle wick, and the creep of a table top spill of water under

the cover of a book.

2. Gravitational Forces These forces are typically very small compared to the cap-

illary forces for small pores in the fuel cell media and can be neglected in the

electrolyte, catalyst larger, and diffusion media but play a key role in ﬂow channels.

3. Convection Forces The importance of this effect depends on the ﬂow ﬁeld design.

4. Evaporation/Condensation These processes also result in signiﬁcant liquid re-

moval and motion.

5. Interfacial Effects The interface between different layers of media can have a

substantial effect on the accumulation and storage of liquid water in porous media

and is an important area of research under development.

5.5.3 Basic Governing Parameters and Relationships of Two-Phase

Flow in Fuel Cell Diffusion Media

Porosity Porous media (PM) is composed of a solid backbone material and void pores.

The volumetric porosity is deﬁned as the ratio of void space to the bulk volume of porous

media containing that void space:

φ =

void volume

total PM volume

(5.85)

The true ﬂow porosity available for multiphase ﬂow represents the interconnected pore

volume that can contribute to ﬂuid ﬂow within the porous media and excludes isolated

pores. Typically, the true ﬂow porosity is slightly less than the volumetric porosity of the

media due to the existence of isolated (orphan) pores.

Wettability When two or more ﬂuids occupy a porous medium, one of the ﬂuids is

absorbed on the surface more strongly and displaces the other ﬂuid. The ﬂuid absorbed

on the surface is called wetting ﬂuid. The displaced ﬂuid is the nonwetting phase. A

porous solid will tend to imbibe the wetting phase while displacing the nonwetting phase

[37] because the wetting phase will compress the nonwetting phase as it is absorbed. On

hydrophobic fuel cell diffusion media surfaces, water will be the nonwetting phase, whereas

gas will be the wetting phase.

Wettability can also be considered as a measure of the speed with which ﬂuids spread

over solid surfaces. The speed of spreading is directly controlled by the interfacial forces at

the solid surface. The spreading can be increased by lower surface tension and lower ﬂuid

viscosity. For two-phase ﬂow in porous media, the wetting angle inﬂuences the capillary

pressure and liquid transport considerably hence, an important aspect of PEFC material

design is hydrophobic content.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

246 Transport in Fuel Cell Systems

Saturation In two-phase systems, the volume fraction of total pore volume occupied by a

phase is termed the phase saturation. Saturation, s, is a key parameter for multiphase ﬂow,

because it represents the available volume through which both phases can still ﬂow. The

phase saturation s

is expressed as

volume taken by phase j

total pore volume

(5.86)

The saturations of all phases (including water, gas, ice, and other ﬂuids) add to unity, that



i=1

= 1 where j represents liquid, gas, and ice phases. For unsaturated ﬂow (most

common in fuel cells), the pore volume is not fully occupied by liquid water and 0 < s

< 1.

The greater the liquid saturation, the greater the restriction in gas-phase transport. The

restriction of the diffusion due to pore saturation can be represented by the effective

saturated porosity:

eff

= φ(1 − s

) (5.87)

This equation can be used to modify the effective diffusion coefﬁcient an catalyst active

surface area under ﬂooded conditions. Another important parameter is irreducible liquid

saturation, also called the immobile saturation (s

irr

), which represents the amount of isolated

trapped water in the pores of the PM. That is, even when a high ﬂow rate of gas is introduced

into the porous media, some fraction of liquid will remain (unless evaporated) primarily

due to discontinuity or isolation with the rest of the pores. The irreducible fraction does

not represent the fraction of liquid in the porous media which cannot be removed from

the fuel cell media. In fact, removal from drag forces is not possible, but removal from

evaporation is.

Contact Angle and Surface Tension Contact angle is a critical parameter in two-phase

ﬂow deﬁned as the angle between the gas–liquid interface and the solid surface. It is

measured at the triple point where all three points intersect. This can be interpreted as

a measure of the wetting of the solid surface by a liquid on different surfaces. Contact

angles depend on the base material of surface temperature, surface impurities, and surface

morphology (roughness).

For a static system, solid surface interfacial tensions can be calculated from the mea-

sured contact angles by using a mechanical equilibrium relation derived by Young in 1800

[38]. The liquid droplet contact angle on any solid surface can be deﬁned by the mechanical

equilibrium of the droplet under the action of three interfacial tensions. The interfacial

tension σ

is deﬁned as the amount of work that must be performed in order to separate a

unit area of ﬂuid j from k.Thetermσ

is the surface tension between substance j and its

own vapor phase (Figure 5.28). The work to separate two phases is expressed as

= γ

+ γ

− γ

(5.88)

Figure 5.28 represents a droplet of liquid l on top of solid s equilibrated with gas g.A

simple force balance on the droplet contact surfaces in the x direction gives the surface

tension components of the solid material:

cos θ =

− γ

(5.89)

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.5 Multiphase Mass Transport in Channels and Porous Media 247

Figure 5.28 Contact angle on a hydrophilic surface.

where γ

, γ

and γ

represent the liquid–vapor, solid–liquid and solid–vapor surface

tensions, respectively. Depending upon the molecular force balance at the contact line, the

surface tends to either contract or stretch the liquid droplet like an elastic membrane.

The angle θ is known as the contact angle. The adhesion tension is γ

cos θ.Ifθ<90

◦

the ﬂuid is termed wetting, and the surface is hydrophilic to the ﬂuid. If θ>90

◦

, the ﬂuid is

called nonwetting and the surface is hydrophobic to the ﬂuid. Consider a droplet of rain on

the hood a polished automobile. The water will bead and is nonwetting on the hydrophobic

surface. On a dirty automobile, the surface is hydrophilic to water, and the water will

spread out and form a sheet. A schematic of a water droplet emerging on a hydrophobic

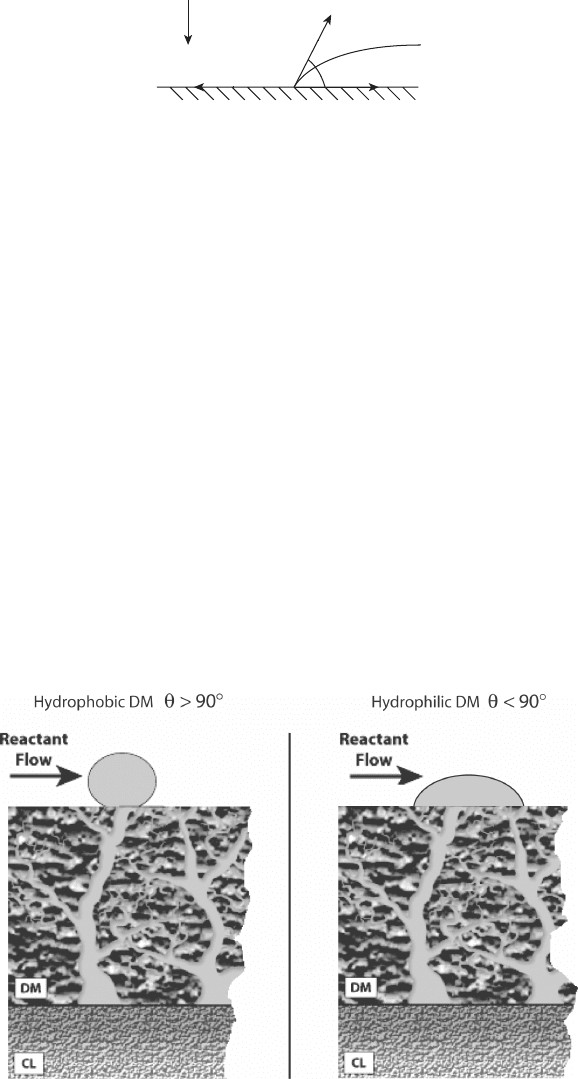
and hydrophilic diffusion media surface is given in Figure 5.29.

In PEFC porous media, the pore size distribution and surface properties are tailored

to achieve the desired two-phase ﬂow characteristics. Typically, highly hydrophobic PTFE

is added to the naturally hydrophilic diffusion media structure. The result is a mixed

hydrophobic–hydrophilic surface and internal structure. Figure 5.30 shows a microscopic

view of a wet diffusion media material.

There is clearly a complex structure of mixed surface tension behavior in these media.

The interrelation of the measured surface-phase tensions as a function of PTFE content for

Figure 5.29 Liquid droplet shape on hydrophobic and hydrophilic DM.

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

248 Transport in Fuel Cell Systems

Figure 5.30 Microscopic view of wet diffusion media paper surface. Some of the surfaces coated

in PTFE in the DM are hydrophobic, while the base carbon ﬁber is hydrophilic. As a result, the

fundamental description of the ﬂow through this medium is extremely difﬁcult [39]. Image courtesy

of Prof. Massoud Kaviani.

SIGRACET carbon-ﬁber-based nonwovens has been correlated [35]:

cos θ

= γ

− γ

= 0.0006 × %PTFE − 0.0274 N/m (5.90)

This linear equation relating γ

− γ

and PTFE content can be used to estimate surface

tension values over the range of 5–20% PTFE loadings. This equation is determined based

on observation of droplets on the surface of the diffusion media; thus the internal structure

and behavior are still the subject of investigation.

Permeability and Darcy’s Law Permeability refers to the tendency of a porous material

to allow ﬂuid to move through its pores. Permeability of a porous medium is one of the

controlling factors that affect the rate at which ﬂuids travels through the pores. For instance,

porous media with higher permeability facilitate the transport of reactants and products.

The intrinsic permeability is a property of the porous media only, not the ﬂowing ﬂuid, and

is deﬁned as

k = Cd

(5.91)

c05 JWPR067-Mench January 23, 2008 18:58 Char Count=

5.5 Multiphase Mass Transport in Channels and Porous Media 249

where k and d are intrinsic permeability and average pore diameter, respectively, and C

represents a dimensionless constant describing the conﬁguration of the ﬂow path. Perme-

ability is either directly measured or empirically estimated using Darcy’s law. Darcy’s law

states that the ﬂow rate through a porous body is equal to the product of the permeability

of the medium and the pressure gradient across the porous body divided by the viscosity

of the ﬂowing ﬂuid:

Q =

−kA

P

(5.92)

This relationship is based on experiments of water ﬂow through a range of sand beds. Here,

Q, A, and µ represent the ﬂow rate, cross-sectional area of ﬂow, and viscosity of the ﬂuid.

The actual permeability of a given phase is given by k, and P/L is the pressure gradient

across the porous medium having a thickness of L. A common unit for permeability is the

darcy (1 darcy ∼10

−12

) in petroleum science, whereas it is represented by centimeters

squared or meters squared in SI units. When a measured value of absolute permeability is

unavailable, the Carman–Kozeny equation can be used to make an estimate of the absolute

gas-phase permeability of the medium:

abs

18τ (1 −φ)

(5.93)

Here, r, φ, and τ are the mean radius of the pores and the porosity and tortuosity of the

medium, respectively.

Relative Permeability In liquid–gas two-phase ﬂow in porous media, the available pore

space is shared by the liquid and gas, and thus the effective cross-sectional area available

for each ﬂuid is less than the total available pore space. This effect is taken into account by

the relative permeability, k

, which is deﬁned as the ratio of the actual permeability for a

phase at a given saturation to the total intrinsic permeability of the porous media:

abs

(5.94)

Thus, the k in Eq. (5.92) must be modiﬁed with k

if there is any saturation. If the porous

media are dry, then k = k

abs

. Direct experimental measurement of relative permeability for

different types of soils has been performed in soil science. However, to date, mathemati-

cal approaches based on previous experiments are commonly preferred for estimating the

relative permeability because of the difﬁculty in conducting direct experiments. Various

researchers have proposed correlations based on experimental data or mathematical deriva-

tions to predict the phase relative permeability. Most of the existing relative permeability

correlations are based on different physical models, including capillary model, statistical

model, empirical model, and network model [40]. Typically, the general shape of the relative

permeability curves can be estimated by the following equations [40]:

r,nw

= A(s

)

and k

r,w

= B(1 − s

)

(5.95)

where nw and w represent the wetting and nonwetting ﬂuids, respectively and A, B, n, and

m are constants depending upon the structure of the porous media. Figure 5.31 depicts a