Медведев Г.А., Морозов В.А. Практикум на ЭВМ по анализу временных рядов
Подождите немного. Документ загружается.

Σ
1
= F
0
Σ
0
F
∗
0
+ Q
1
, Σ
0
= M{(m
0
− M{m
0
})(m
0
− M{m
0
})
∗
}. (4.89)
Оптимальная в среднеквадратичном смысле линейная оценка фильтрации
˜
m
N
определяется следующими соотношениями:
˜
m
N
=
ˆ
m
N
+
˜
K
N
(x
N
− H
N
ˆ
m
N
), N = 1, 2, . . . , (4.90)
где (n × m)-матрица
˜
K
N
находится по формуле
˜
K
N
= Σ
N
H
∗
N
(H
N
Σ
N
H
∗
N
+ R
N
)
−1
, (4.91)
а корреляционная матрица ошибок фильтрации
˜
Σ
N
= M{(m
N
−
˜
m
N
)(m
N
−
˜
m
N
)
∗
}
определяется по формуле
˜
Σ
N
= (I −
˜
K
N
H
N
)Σ
N
, (4.92)
где I — единичная матрица.
Сравнение формул (
4.87)—(4.92) позволяет заключить, что о цен ки предска-
зания и фильтрации и корреляционные матрицы ошибок предсказания и филь-
трации связаны простыми соотношениями:
ˆ
m
N+1
= F
N
˜
m
N
, N = 1, 2, . . . ; (4.93)
Σ
N+1
= Q
N+1
+ F
N
˜
Σ
N
F
∗
N
. (4.94)
Это позволяет наиболее рационально построить пр оце сс последовательного
вычисления оценок предсказания и фильтрации.
Э т а п 1. Определяется
ˆ
m
t
по (
4.93) (для t = 1 по (4.87)).
Э т а п 2. Определяется
˜
Σ
t
по (4.94) (для t = 1 по (4.89)).
Э т а п 3. Определяется
˜
K
t
по (4.91).
Э т а п 4. Определяется
˜
m
t
по (4.90).
Э т а п 5. Определяется
˜
Σ
t
по (4.92).
После каждой итерации значение индекса t увеличивается на единицу и про-
цедура повторяется. Заметим, что для определения корреляционных свойств (и,
в частности, дисперсий) оценок нет необходимости использовать этапы 1 и 4,
на которых подсчитываются сами оценки. Добавим, что оценки фильтрации и
предсказания с ростом N модернизируются в зависимости от са мих выб оро чных
значений x
N
. Причем при определении очередной оценки требуется использо-
вать только одну последнюю инновацию.
Временной ряд, заданный уравнениями (4.92), (4.93), является более общим
описанием процессов типа АРСС. Покажем это. Пусть y
t
— процесс АРСС (p, q),
описываемый уравнениями (4.28). Представим его в более удобной форме
y
t
=
n
X
j=1
(a
j
y
t−j
+ b
j−1
W
t+1−j
), (4.95)
120
где n = max{p, 1 + q}; a
i
= 0, i > p; b
i
= 0, i > q.
Определим вектор m
t
= (m
t1
, . . . , m
tn
) с компонентами m
tj
= y
t−i+1
; F —
(n × n)-матрица с элементами T
ij
= b
j
δ
1j
; v
t
— вектор с компонентами v
tj
=
= W
t+1−j
, 1 ≤ j ≤ n. Составим векторное равенство
m
t+1
= F m
t
+ T v
t+1
. (4.96)
В этом равенстве первая компонента полностью совпадает с уравнением (
4.95),
а остальные компоненты являются тождествами y
t−i+1
≡ y
t−i+1
, 2 ≤ i ≤ n.
Сравнивая (4.96 ) с (4.82), убеждаемся в том, что уравнение (4.92) в частном
случае, когда F
t
= F , V
t
= T v
t
, приобретает вид (4.96). Причем матрица Q =
= M{V
t
V
∗
t
} = σ
2
TT
∗
. Она не меняется с возрастанием t и имеет единственный
ненулевой элемент Q
11
= σ
2
q
P
j=0
b
2
j
.
Далее, если мы определи м (1 × n)-матрицу H
t
= (1 0 0 . . . 0) и W
t
= 0, то
уравнение (4.84) вырождается в уравнение наблюдения временного ряда x
t
= m
t
с нулевыми ошибками наблюдения.
Таким образом, уравнение процесса АРСС (p, q) является частным случа-
ем уравнений (
4.82)—(4.84). Поэтому полученные в § 4.1—4.4 уравне ния оценки
предсказания процесса авторегрессии могут быть выражены в форме (4.90)—
(4.94).
Калмановские оценки фильтрации и прогнозирования довольно просты и
удобны для организации вычислений. Однако их практическое использование
показало, что может возникнуть неустойчивость при определении оценок и
процесс оценивания может расходиться. Это возникает тогда, когда парамет-
ры уравнений (4.82)—(4.85) известны неточно. Такая ситуация возникает, когда
предсказанию процесса предшествует этап оцен ива ния неизвестных параметров
модели временного ряда и в д аль ней шем используются не точные значения па-
раметров уравнений (4.82)—(4.85), а их выборочные оценки. В результате такой
неточности оценка вычисляется неверно, эти ошибки накапливаются, и оцен-
ки могут отличаться очень си ль но. Проблема становится особенно острой,
когда член, соответствующий шуму, в уравнениях системы мал. Тогда малы
ковариации ошибок и коэффициент усиления Калмана, а последующие наблю-
дения незначительно влияют на оценивание. При практических применениях
расходимость проявляет себя через об нов лен ие. В результате оценка больше не
оптимальная, матрица Σ
t
не является меро й дисперсии ошибок оценивания, и
ошибка ( ˆm
t
− m
t
) систематически увеличивается с ростом t.
Один из способов борьбы с расходимостью оценки состоит в модификации
уравнений оценки таким обра зом, чтобы более свежие наблюдения имели боль-
шее влияние на оценки, а воздействие старых наблюдений постепенно уменьша-
лось. Этого можно достичь использовани ем весов α
i
к наблюдениям y
t−i
, таких,
что α
i
монотонно уменьшается с ростом i. Наиболее удобными являются веса
степенного вида α
i
, 0 < α < 1. В случае применения весов уравнения (4.91)
и (4.92), определяющ ие коэффициент усиления и матрицу ковариации оценок
121
фильтрации, заменяются на следующие:
˜
K
N
= Σ
N
H
∗
N
(H
N
Σ
N
H
∗
N
+ αR
N
)
−1
, (4.97)
˜
Σ
N
= α(I −
˜
K
N
H
N
)Σ
N
, (4.98)
Остальные уравнения остаются без изменения. Если в (
4.97), (4.98) положить
α = 1, то эти формулы превращаются в (4.89), (4.91). Каких-либо конкретных
указаний выбора α сформулировать не удается, так как расходимость оценок
зависит от соотношения параметров уравнений ( 4 .82 ), (4.84), а также от тех
неточностей, которые допущены при оценивании этих параметров.
Лабораторная работа 19. Калмановская фильтрация
и прогнозирование
Цель работы. Освоить технику вычисления оценок фильтрации и оценок
предсказания при помощи рекуррентных процедур Калмана. Изучить проблему
устранения расходимости рекуррентных оценок Калмана.
Порядок выполнения работы
Задание 1. Выбрать какую-либо модель ПАРСС (p, d, q), желательно уже
исследованную ранее при выполнении лабо рат орн ой работы 17. Построить для
нее разностные векторно-матричные уравнения (4.82)—(4.84). Задать ненулевой
шум наблюдения в уравнении (4.84). При помощи моделирования в соответствии
с этими уравнениями получить реализацию п роц есса x
t
. Сравнить эту реализа -
цию с реализацией процесса из лабораторной работы 17. Изобразить обе реа-
лизации на графике. Установить, насколько сильно искажает шум наблюдения
исследуемый процесс. По формул ам (4.87)—(4.94) построить оценки фильтрации
и прогнозирования исследуемого процесса, имея в виду первую компоненту век-
тора m
t
. Вычислить точность предсказания процесса и сравнить эту точность с
точностью предсказания, получен ной при выполнени и лабораторной работы 17.
Объяснить различие в этих результатах.
Задание 2. Выбрать произвол ьные матрицы F
t
и H
t
в уравнениях (4.82),
(4.84). Задать положительно определенные матрицы R
t
, Q
t
. (Для простоты ис-
следования матрицы можно выбирать не зависящими от t.) Получить реализа-
цию процессов. Построить оценки предсказания и фильтрации. Затем исказить
одну из матриц F, H, R, Q и с использованием этой матрицы построить снова
оценки предсказания и фильтрации процесса. ( При искажении матриц R и Q
необходимо это делать так, чтобы искаженные матрицы оставались положитель-
но определенными.) Установить расходимость оценок. Исследовать, к какой рас-
ходимости приводит искажение той или иной матрицы. Использовать формул ы
(4.97), (4.98) с целью устранения расходимости. Исследовать влияние величины
параметра α в формулах (4.97), (4.98) на качество устранения расходимости и
на качество оценивания и предсказания. Исследования иллюстрировать графи-
ками.
122
Глава 5
СПЕКТРАЛЬНЫЙ АНАЛИЗ ВРЕМЕННЫХ РЯДОВ
5.1. Спектральные представления СП и оценивание
спектральных плотностей
Для любого стационарного СП (ССП) {x
t
, t = 0, ±1, ±2, . . .} можно постро-
ить процесс {y
t
, t = 0, ±1, ±2, . . .}, определяемый представлением
y
t
= m +
n
X
j=1
(A
j
cos λ
j
t + B
j
sin λ
j
t), t = 0, ±1, . . . , (5.1)
где m = M{x
t
}; {A
j
}, {B
j
} — СВ со свойствами M{A
j
} = M{B
j
} = 0;
M{A
2
j
} = M{B
2
j
} = σ
2
j
; M{A
j
B
j
} = 0 для любых j, 1 ≤ j ≤ n; λ
j
принима-
ют значения на отрезке [0, π]. АКФ процесса {y
t
} при помощи со отве тст вую-
щего выбора {σ
2
j
, 1 ≤ j ≤ N } может хорошо а пп роксимировать АКФ процесса
{x
t
}. Выбрав n д остаточно большим, можно получить сколь угодно хорошую
аппроксимацию исходного процесса и его АКФ. Такая декомпозиция ССП в
сумму гармонических составляющих с некоррелированными случайными коэф-
фициентами соответствует спектральному представлению ССП, рассматривав-
шемуся в гл.1. Декомпозиция ССП влечет за собой и декомпозицию АКФ этого
ССП. Анализ ССП при помощи их спектр аль ных представлений часто назы-
вается анализом в “частотной области”, поскольку веществен ный параметр λ в
(
5.1) принято называть частотой (радианной, угловой и т.д.). Этот анализ яв-
ляется эквивалентом анализу во “временной области”, осно ванному на АКФ,
но иногда обеспечивает способ рассмотрения процесса, который для некоторых
применений более понятен. Такие примеры имеются в физике, электротехнике,
акустике, геофизике и других разделах техники, а также в медицине, экономике,
биологии, психологии и численном анализе.
Учитывая свойства {y
t
}, определенного в (5.1) по отношению к ССП {x
t
} с
нулевым средним, представим {x
t
} в виде
x
t
=
n
X
j=1
a
j
e
itλ
j
, (5.2)
где −π < λ
1
< λ
2
< . . . < λ
n
≤ π; {a
j
} — некоррелированные, вообще говоря,
комплексные СВ, такие, что M{a
j
} = 0, M{a
j
¯a
j
} = σ
2
j
, 1 ≤ j ≤ n. Здесь ¯a —
комплексно-сопряженная СВ по отношению к a. В ча стн ом случае , когда {x
t
} —
вещественный СП, λ
j
= −λ
n+1−j
и a
j
= ¯a
n+1−j
, 1 ≤ j ≤ n (интересно отметить,
что, несмотря на последнее равенство, a
j
и a
n+1−j
— некоррелированные СВ):
M{x
t
x
t+τ
} = r(τ) =
n
X
j=1
σ
2
j
e
iτλ
j
. (5.3)
123

Определим F (λ) =
P
j:λ
j
≤λ
σ
2
j
— непрерывную справа неубывающую функцию,
такую, что F (−π) = 0, F (π) = r(0). Записывая (
5.3) в виде интеграла Римана—
Стилтьеса, получаем
r(τ) =
π
Z
−π
e
iτλ
dF (λ). (5.4)
Функция F (λ) называется спектральной функцией (спектральной мерой, функ-
цией спектрального распределения).
Более общим, чем пред ставление (
5.2), является с пек тра льн ое представление
ССП с нулевым средним
x
t
=
π
Z
−π
e
itλ
dz, (5.5)
в котором z(λ) — случа йный процесс с ортогональными приращениями, обычно
называемый спектральным процессом. Соответственно АКФ r(τ) процесса x
t
выражается в виде (
5.4). Если в (5.4) F (λ) абсолютно непрерывна, т.е.
F (λ) =
λ
Z
−π
f(ν) dν, −π ≤ λ ≤ π, (5.6)
то f(ν) называется спектральной плотностью процесса x
t
. Если r(τ ) — абсо-
лютно суммируемая функция, т.е.
+∞
P
τ=−∞
|r(τ)| < ∞, то имеет место представле-
ние
f(λ) =
1
2π
+∞
X
τ=−∞
e
−iτλ
r(λ), −π ≤ λ ≤ π. (5.7)
Отсюда, в частности, следует, что для вещественных x
t
f(λ) является четной.
Пусть {x
t
} — процесс АРСС (p, q) (не обязательно каузальный и обратимый),
определяемый разностным уравнением
x
t
=
p
X
i=1
a
i
x
t−i
+
q
X
j=0
b
j
W
t−j
, (5.8)
где W
t
— белый шум с дисперсией σ
2
. Если полиномы a(z) = 1 −a
1
z −. . . −a
p
z
p
,
b(z) = 1 + b
1
z + . . . + b
q
z
q
не имеют общих корней и a(z) не имеет корней на
окружности |z| = 1, то спектральная плотность процесса АРСС (p, q) выража-
ется равенством
f(λ) =
σ
2
|b(e
−iλ
)|
2
2π|a(e
−iλ
)|
2
, −π ≤ λ ≤ π, (5.9)
т.е. является рациональной спектральной плотностью.
124

Если f(λ) — непрерывная спектральная плотность некоторого вещественного
ССП и ε > 0, то, во-первых, существ ует обратимый СС (q)-процесс x
t
= W
t
+
b
1
W
t−1
+ . . . + b
q
W
t−q
, такой, что |f
x
(λ) − f (λ)| < ε для всех −π ≤ λ ≤ π, где
W
t
— белый шум с дисперсией σ
2
, причем σ
2
= (1+ b
2
1
+. . . +b
2
q
)
−1
π
R
−π
f(λ) dλ, во-
вторых, существует каузальный АР (p)-процесс x
t
= a
1
x
t−1
+ . . . + a
p
x
t−p
+ W
t
,
такой, что |f
x
(λ) − f(λ)| < ε для всех −π ≤ λ ≤ π, где W
t
— белый шум с
дисперсией σ
2
.
Рассмотрим произвольное множество н абл юде ний {x
1
, x
2
, . . . , x
N
}, сделан-
ных в моменты t = 1, 2, . . . , N. Предположив выборку {x
t
, 1 ≤ t ≤ N } пе-
риодической с периодом N, представим ее элементы в виде декомпозиции по
гармоникам ω
j
:
x
t
=
1
√
N
X
−π<ω
j
≤π
a
j
e
itω
j
, t = 1, . . . , N, (5.10)
где частоты ω
j
= 2πj/N = j(2π/N ), ω
j
∈ (−π, π], называются частотами Фу-
рье ряда {x
1
, x
2
, . . . , x
N
}. Вводя вектор-столбец e
j
=
1
√
N
(e
iω
j
, e
i2ω
j
, . . . , e
iNω
j
)
∗
,
совокупность соотношений (5.10 ) можно записать в векторной форме x =
= (x
1
, . . . , x
N
)
∗
:
x =
X
j∈J
N
a
j
e
j
, (5.11)
где J
N
= {j : −π < ω
j
=
2πj
N
≤ π} = {−
£
N−1
2
¤
, . . . ,
£
N
2
¤
}; [a] — целая часть
числа a; J
N
содержит N целых чисел. Разложение (
5.11) обладает следующи-
ми свойствами: векторы {e
j
} образуют ортогональный базис, коэффициенты a
j
имеют вид
a
j
=
1
√
N
N
X
t=1
x
t
e
−itω
j
. (5.12)
Таким образом, {a
j
, j ∈ J
N
} — это дискретное преобразование Фурье (ДПФ)
выборки {x
t
, 1 ≤ t ≤ N }.
Функция I(ω), определенная на множестве частот {ω
j
}, значения которой
определяются по формуле
I(ω
j
) = |a
j
|
2
=
1
N
¯
¯
¯
¯
¯
N
X
t=1
x
t
e
−itω
j
¯
¯
¯
¯
¯
2
, −π < ω
j
=
2πj
N
≤ π, (5.13)
называется периодограммой. Периодограмма представляет разложение ||x||
2
на
сумму компонент, связанных с частотами Фурье:
||x||
2
=
X
j∈J
N
I(ω
j
). (5.14)
125
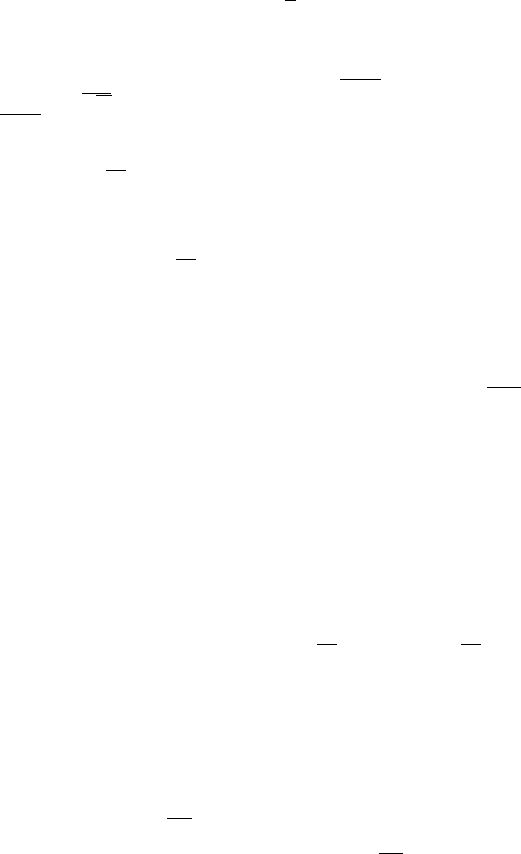
Если x — вещественный ССП, то для всякого j ∈ J
N
всегда ω
j
∈ [−π, π] и
−ω
j
∈ [−π, π], п оэт ому a
j
= ¯a
j
и I(ω
j
) = I(−ω
j
). Тогда (
5.10) приобретает вид
x = a
0
e
0
+
[(N−1)/2]
X
j=1
(a
j
e
j
+ ¯a
j
e
−j
) + a
N/2
e
N/2
, (5.15)
где последнее слагаемое равно нулю, если N — нечетное. Представим комплекс-
ные коэффициенты a
j
в виде α
j
e
iβ
j
, тогда (
5.15) перепишем следующим образом:
x = a
0
e
0
+
[(N−1)/2]
X
j=1
√
2α
j
(c
j
cos β
j
− s
j
sin β
j
) + a
N/2
e
N/2
, (5.16)
где e
0
=
1
√
N
(1 1 . . . 1)
∗
; c
j
=
p
2/N(cos ω
j
, cos 2ω
j
, . . . , cos Nω
j
)
∗
; s
j
=
=
p
2/N(sin ω
j
, sin 2ω
j
, . . . , sin Nω
j
)
∗
.
Пусть ˆm =
1
N
N
P
t=1
x
t
и ˆr(τ ) — выборочная АКФ:
ˆr(τ ) =
1
N
N−|τ|
X
t=1
(x
t+|τ|
− ˆm)(x
t
− ˆm), 0 ≤ |τ| < N, (5.17)
тогда I(ω
j
), определенная формулой (
5.13), может быть представлена в виде
I(ω
j
) =
X
|τ|<N
ˆr(τ )e
−iτω
j
, ω
j
=
2πj
N
. (5.18)
Сравнивая (
5.18) с (5.7), приходим к выводу, что периодограмма I(ω
j
) может
быть использована для оценивания спектральной плотности f (λ). В связи с этим
отметим некоторые свойства периодограммы. Пусть {x
t
} — ССП со средним
значением m и абсолютн о суммируемой АКФ r(τ ). Его спектральная плотность
f(λ) является непрерывной функцией и задается формулой (5.7). Назовем рас-
ширенной периодограммой I
N
(λ) функцию
I
N
(λ) =
½
I(ω
j
), ω
j
−
π
N
< λ ≤ ω
j
+
π
N
, λ ∈ [0, π],
I
N
(−λ), λ ∈ [−π, 0].
(5.19)
При N → ∞ будем иметь
M{I
N
(0) − Nm
2
} → 2πf(0); M{I
N
(λ)} → 2πf(λ), λ 6= 0. (5.20)
Отсюда следует, что
1
2π
I
N
(λ) для λ 6= 0 является асимптотически несмещен ной
оценкой спект рал ьно й плотности f(λ), а
1
2π
(I
N
(0) − N m
2
) — асимптотически
несмещенной оценкой f(0).
126

Как уже отмечалось, многие с луча йные процессы, порождающие наб людае-
мые временные ряды, могут быть представлены в виде
x
t
=
+∞
X
j=−∞
ψ
j
W
t−j
, t = 0, ±1, ±2, . . . ,
где W
t
— белый шум с дисперсией σ
2
, а
+∞
P
−∞
|ψ
j
| < ∞. Тогда если f(λ) > 0 для всех
λ ∈ [−π, π] и если 0 < λ
1
< λ
2
< . . . < λ
n
< π, то случайный вектор, составлен-
ный из значений периодограммы (
5.19) (I
N
(λ
1
), . . . , I
N
(λ
n
))
∗
, сходится по рас-
пределению при N → ∞ к вектору с независимыми и экспоненциально распреде-
ленными компонентами со средним значением (2πf (λ
1
), 2πf(λ
2
), . . . , 2πf(λ
n
))
∗
.
При этом если
+∞
P
j=−∞
p
|j||ψ
j
| < ∞, M{W
4
t
} < ∞, то
cov(I
N
(ω
j
), I
N
(ω
k
)) =
2(2π)
2
f
2
(ω
j
) + 0(
1
√
N
), ω
j
= ω
k
= 0 или π,
(2π)
2
f
2
(ω
j
) + 0(
1
√
N
), 0 < ω
j
= ω
k
< π,
0(
1
√
N
), ω
j
6= ω
k
,
(5.21)
где ω
j
= 2πj/N — частоты Фурье для выборки {x
1
, x
2
, . . . , x
N
}.
Отсюда следует, что хотя пери одограмма является асимптотически несме-
щенной оценкой 2πf(λ), однако она не является состоятельной оценкой этой в е-
личины. Вместе с тем значения I
N
(λ) для различных λ, принимающих значения
из множества частот Фурье, являются асимптотически некоррелированными.
Поэтому, рассматривая компоненты вектора (I
N
(ω
1
), . . . , I
N
(ω
[N/2]
))
∗
как функ-
ции ω
j
, можно убедиться, что они образуют сильно флуктуирующий процесс со
средним значением, аппроксимирующим 2πf(λ). Представляется возможность
использовать сглаживающий фильтр для этого процесса, причем его характе-
ристики выбираются таким обр азом, чтобы образуемая им функция была не
только асимптотически несмещенной, но и состоятельной оценкой с пек тра ль-
ной плотности. Иначе говоря, введем оценку спектральной плотности (ОСП):
ˆ
f
g
(ω
j
) =
1
2π
X
|k|≤n
g
N
(k)I
N
(ω
j+k
), (5.22)
где n — некоторое цело е число; g
N
(k) — последовательность некоторых весовых
коэффициентов. В условиях справедливости (5.21) относительно свойс тв (5.22)
можно записать:
lim
N → ∞
cov(
ˆ
f
g
(λ),
ˆ
f
g
(ν))
P
|k|≤n
g
2
N
(k)
=
2f
2
(λ), λ = ν = 0 или π,
f
2
(λ), 0 < λ = ν < π,
0, λ 6= ν.
(5.23)
127
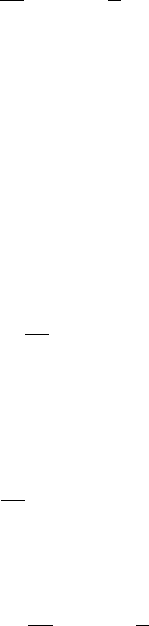
Из (5.22) и (5.23) видно, что для асимптотической несмещенности и состоятель-
ности необходимо и достаточно выполнение следующих условий, влияющих на
характер изменения весовых коэффициентов. Для асимптотической несмещен-
ности
X
|k|≤n
g
N
(k) = 1. (5.24)
Для состоятельности
lim
N → ∞
X
|k|≤n
g
2
N
(k) = 0. (5.25)
Будем полагать также g
N
(k) = g
N
(−k). В специальной литературе весовые ко-
эффициенты g
N
(k) обычно называются сглаживающим фильтром.
Часто используется иная оценка сп ектр ал ьно й плотности, которая построена
на модификации представления периодограммы в виде (
5.18):
ˆ
f(λ) =
1
2π
X
|τ|≤n
h
³
τ
n
´
ˆr(τ )e
−iτλ
, (5.26)
где h(t) — четная кусочно-непрерывная функция, удовлетворяющая условиям
h(0) = 1, |h(t)| ≤ 1 для всех t, h(t) = 0 для |t| > 1; ˆr(τ ) — выборочная АКФ.
Задав расширенную периодограмму соотношением
I
N
(λ) =
X
|τ|≤N
ˆr(τ )e
−iτλ
, (5.27)
совпадающим с (5.19) на множестве частот Фурье (см. также (5.18)), получим
представление для выборочной АКФ
ˆr(τ ) =
1
2π
π
Z
−π
e
iτλ
I
N
(λ) dλ, (5.28)
при подстановке которого в (
5.26) найдем еще одно представление оценки спек-
тральной плотности
ˆ
f(λ) =
1
2π
π
Z
−π
H(ν)I
N
(ν + λ) dν, (5.29)
где функция H(λ) определяется соотношением
H(λ) =
1
2π
X
|τ|≤n
h
³
τ
n
´
e
−iτλ
(5.30)
и называется спектральным окном (частотным окном). Соответственно этому
h(t), удовлетворяющая (5.26), называется корреляционным окном (временным
окном).
128
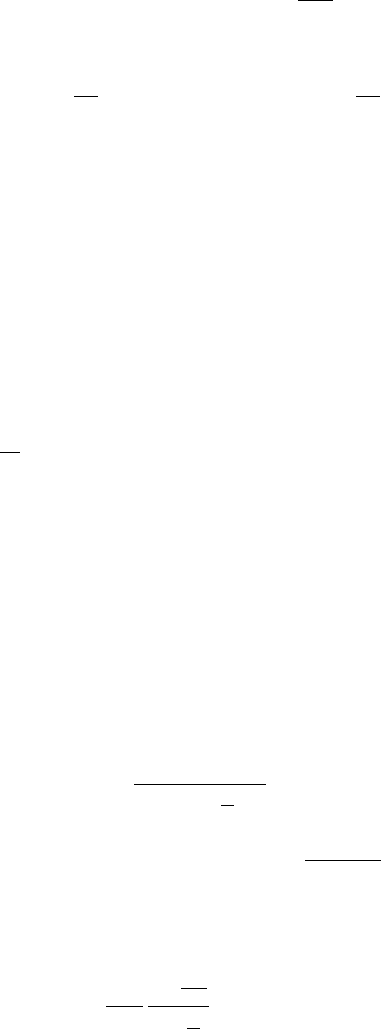
Разбив интервал [−π, π] частотами Фурье ω
j
=
2πj
N
и заменив интеграл (
5.29)
интегральной суммой, получим еще одну ОСП
ˆ
f(λ) =
1
2π
[N/2]
X
j=1−[N/2]
H(ω
j
)I
N
(λ + ω
j
)
2π
N
. (5.31)
Формулу (
5.31) можно рассматривать как приближение оценки (5.26) при помо-
щи взвешенного усреднения периодограммы I
N
(ω) с весами H
j
= 2πH(ω
j
)/N,
|j| ≤ [N / 2]. Следует заметить, что весовые коэффициенты H
j
не о бязатель-
но должны удовлетворять условиям типа (5.24), (5.25), которые требуются при
построении ОСП (5.2 2 ) при помощи взвешенного усреднения периодограммы
I
N
(ω) с весами g
N
(k).
В условиях справедливости (5.21) lim
N → ∞
M{
ˆ
f(λ)} = f(λ), 0 ≤ λ ≤ π, и вы-
полняется предельное соотношение
lim
N → ∞
N
n
D{
ˆ
f(λ)} =
2f
2
(λ)
+1
R
−1
h
2
(t)dt, λ = 0 или π,
f
2
(λ)
+1
R
−1
h
2
(t)dt, 0 < λ < π.
Отсюда следует состоятельность и асимптотическая несмещенность оценки
(
5.26).
В (5.26) корреляционное окно h(t) за дае тся неоднозначно. Поэтому суще-
ствует достаточно много вариантов определения этих окон. Приведем наиболее
известные варианты вместе с сопутствующими им спектральными окнами H(λ).
Окно Дирихле (прямоугольное, усеченное окно):
h(t) = 1, 0 ≤ |t| ≤ 1;
H(λ) = D
n
(λ) =
sin (n + 1/2)λ
2πsin
λ
2
, −π ≤ λ ≤ π, (5.32)
D
n
(λ) — ядро Дирихле. В этом случае D{
ˆ
f(λ)}
∼
=
2nf
2
(λ)
N
.
Окно Бартлетта (треугольное окно):
h(t) = 1 − |t|, 0 ≤ |t| ≤ 1,
H(λ) =
1
2πn
sin
nλ
2
sin
λ
2
, −π ≤ λ ≤ π. (5.33)
B этом случае спектральное окно имеет название ядро Фейера и отличается от
ядра Дирихле т ем, что принимает только неотрицательные значения. Дисперсия
оценки спектральной плотности (ОСП) в этом случае приблизительно равн а
2nf
2
(λ)/3N.
129
