Медведев Г.А., Морозов В.А. Практикум на ЭВМ по анализу временных рядов

Подождите немного. Документ загружается.

времени, оценить для каждого ряда момент разладки t

и вычислить среднюю

величину

t =

i=1

Глава 4

ПРОГНОЗИРОВАНИЕ ВРЕМЕННЫХ РЯДОВ

4.1. Прогнозирование тренда

Прогнозирование (предсказание) временного ряда является важной практи-

ческой задачей. Вообще говоря, определение математического описания времен-

ного ряда, его параметров — это вспомогательная задача, которую необходи мо

решить, чтобы воспользоваться ею для предсказания. Наиболее типичное пред-

сказание — прогноз погоды. Однако погода о пи сывает ся сложно, зависит от

многих детерминированно и случайно изменяющихся факторов и не может слу-

жить примером временного ряда. Обратимся к более простым ситуациям.

Временной ряд, как в большинстве рассмотренных случаев, представим в

виде

= m

+ y

, t ∈ T = {t

, t

, . . . , t

}, (4.1)

где m

— детерминированная или стохастическая составляющая, которая по-

рождается определенным закономерным образом, быть может, неизвестным и с-

следователю; y

— случайная составляющая, независимая от m

, являющаяся

реализацией некоторого ССП. Для определенности в дальнейшем считаем, что

< t

i+1

для всех i, и пишем вместо x

более кратко x

, полагая t

= i.

В рамках такой модели могут быть сформул иро ван ы следующие задачи, свя-

занные с предсказанием:

1) по наблюдениям {x

, x

, . . . , x

} предсказать значение m

N+k

, k > 0;

2) по наблюдениям {x

, x

, . . . , x

} предсказать значение x

N+k

, k > 0.

При решении первой задачи возможны два варианта: m

является детерми-

нированным трендом, m

— случайный процесс.

Поскольку в (

4.1) m

и y

независимы между собой, при решении второй за-

дачи требуется вначале решить первую, затем, имея в виду, что y

— ненаблюда-

емый процесс, определить его как остатки x

− m

и осуществить предсказание

значения y

N+k

по множеству остатков {x

−m

, 1 ≤ i ≤ N}. Из вышеуказанных

свойств след ует, что процесс x

− m

является стационарным СП, поэтому воз-

никает задача предсказания данного процесса. Таким образом, будут найдены

предсказанное значение ˆm

N+k

и предсказанное значение ˆy

N+k

, сумма которых

и даст предсказанное значение ˆx

N+k

Прежде чем переходить к конкретным оценкам предсказания, рассмотрим

некоторые общие вопросы. Будем считать, что временной ряд {x

, t ∈ T }, T = {1,

2, . . . , N}, порождается СП с ограниченным вторым моментом, т.е. M{x

} < +∞

∀ t. Предсказание величины x

N+τ

временного ряда, τ > 0, по наблюдениям {x

, . . . , x

} сводится к нахождению детерминированной функции N аргументов,

значения которой можно было бы принимать в качестве x

N+τ

, т.е.

ˆx

N+τ

= f(x

, x

, . . . , x

), τ > 0. (4.2)

Среди всевозможных функций (4.2) представляет ин тер ес та, которая дает наи-

лучшее предсказание. В анализе временных рядов принято считать наилуч-

шим такое предсказание (прогнозирование), которое обеспечивает минималь-

ную среднеквадратичную ошибку предсказания, иными словами функция (4.2)

должна быть решением следующего экстремального уравнения:

M{(x

N+τ

− ˆx

N+τ

)

} = M{(x

N+τ

− f(x

, x

, . . . , x

))

} → min

f(·)

. (4.3)

Эта задача имеет единственное решение

ˆx

N+τ

= f(x

, x

, . . . , x

) = M{(x

N+τ

, x

, . . . , x

}. (4.4)

Таким образом, оптимальное предсказание — это вычисление условного мате-

матического ожидания п ред сказываемого значения при фиксированных наблю-

даемых значениях временного ряда.

Рассмотрим случай нормального распределения. Предположим, что имеют-

ся наблюдения N значений временного ряда {x

, x

, . . . , x

}. Составим из них

вектор-столбец x(1, N ) = (x

, x

, . . . , x

)

∗

. Полагаем, что структура временно-

го ряда определена формулой (4.1), где m

— детерминированная компонента,

которая в данном случае определяет математическое ожидание x

так, что

M{x(1, N)} = m(1, N) = (m

, m

, . . . , m

)

∗

. (4.5)

Необходимо по наблюдениям x(1, N ) построить прогноз значений временно-

го ряда для значений параметра, определяемых неравенствами N + k ≤ t ≤

≤ N + k + n − 1, т.е. с учетом вектора x(1, N) п ред сказать значения {x

N+k

N+k+1

, . . . , x

N+k+n−1

}. Для удобства обозначим

x(1, n) = (ˆx

, ˆx

, . . . , ˆx

)

∗

, где

ˆx

— оценка x

N+k+j−1

. Итак, зная вектор x(1, N) прошлых значений временного

ряда, необходимо оценить n будущих значений этого временного ряда, представ-

ленных вектором

x(1, n). Предполагается, что распределение значений времен-

ного ряда нормальное, так что совместная пло тно сть x(1, N) и

x(1, n) имеет

вид

p(x,

x) =

√

detK

(2π)

n+N

−

x − m

ˆx − ˆm

∗

x − m

ˆx − ˆm

, (4.6)

где K — матрица, обратная матрице ковариаций составного вектора (x

∗

), т.е.

−1

xˆx

ˆxx

ˆxˆx

, (4.7)

m — векто р математических ожиданий x(1, N);

m — векто р математических

ожиданий вектора

x(1, n).

Пусть векторы m,

m и матрица K известны. Тогда наилучшее предсказание,

соответствующее (

4.4), приводит к соотношению

x(1, n) =

m(1, n) + Σ

ˆxx

−1

(x(1, N) − m(1, N)). (4.8)

При этом корреляционная матрица ошибок предсказания ε(1, n) = (ε

, . . . , ε

)

∗

, ε

= ˆx

− x

N+k+j−1

, имеет структуру

εε

= Σ

ˆxˆx

− Σ

ˆxx

−1

xˆx

. (4.9)

Характерной особенностью оптимальной оценки предсказания нормально

распределенного временного ряда является тот факт, что предсказание значе-

ния временного ряда — линейные функциии наблюдений, т.е. выражения (

4.8)

можно представить в виде

x(1, N) = a + Bx(1, N), (4.10)

где a — ср едн ее значение прогноза a =

m(1, n) − Σ

ˆxx

−1

m(1, N). B = =

ˆxx

−1

— (n × N)-матрица коэффициентов регрессии предсказываемых зна-

чений имеющихся наблюдений. Из полученнного результата следует, что для

построения прогноза на n значений временного ряда по N наблюдениям необхо-

димо знать вект ор ы математических ожиданий m(1, N),

m(1, n) и корреляцион-

ные матрицы Σ

, Σ

xˆx

, Σ

ˆxx

, Σ

ˆxˆx

. Иными слов ами, при построении оптимального

прогноза (

4.4) требуется большое количество сведений о предсказываемом СП.

Если временной ряд порождается СП, отличающимся от нормального, необ-

ходимо еще знать много мерно е совместное распределение данного процесса. Это

требование являе тся наиболее труд нов ыполн имым. Проблемы, связанные с про-

гнозированием случайн ых процессов в общем случае, будут обсуждены в после-

дующих параграфах. Обратимся к задаче прогнозирования значений детерми-

нированного тренда m

в модели (4.1).

Пусть наблюдается временной ряд (4.1) с неизвестным детерминирован-

ным трендом m

и случайной компонентой y

. Требуется по N наблюдениям

, x

, . . . , x

} найти прогноз значений {m

N+k

, m

N+k+1

, . . . , m

N+k+n−1

} тренда

. Для этой задачи надо воспользоваться техникой оценивания функции ре-

грессии (§ 2.2), которая сводится к следующему. Пусть наблюдения временного

ряда известны для некоторого множества T значений параметра t. Необходимо

определить прогноз детерминированного тренда для значений t из множества

T ,

T ∩ T = ®. Объедин им эти множества: = = T ∪

T . Выберем отрезок число-

вой оси [a, b], в который бы п огр ужалось множество =, т.е. = ⊆ [a, b]. Введем

линейное преобразование параметра t так, чтобы отрезок [a, b] отображался в

[+1, −1]. Исходя из практическ их соображений, связанных с конкретным харак-

тером временного ряда, выберем систему ортогональных или линейно независи-

мых функций {ϕ

(u)}. Методом наимен ьши х квадратов найдем коэффициенты

разложения m

по базису {ϕ

(u)}, а именно:

m(u) =

j=1

(u) = c

∗

ϕ(u), (4.11)

где переменная u связана с пераметром t соотношением u = (2t −b −a)/(b −a);

c =

i=1

ϕ(u

)ϕ

∗

)

−1

i=1

ϕ(u

). (4.12)

Таким образом, прогнозируемые значения временного ряда m

N+k+l−1

= m(u

1 ≤ l ≤ n, определяются по формуле

m(u

) = c

∗

ϕ(u

), u

∈

U, (4.13)

где c задано в (

4.12);

U — образ множества

T , соотв етст вующ ий описанному

линейному пр еоб раз ова нию параметра t в u. Возвращаясь теперь к исходной

переменной t

= ((b −a)u

+ a + b)/2, получим оцениваемые значения ˆm

N+k+l−1

Лабораторная работа 12. Прогнозирование нормально

распределенных временных рядов

Цель работы. Исследовать характер изменения качества прогнозирования

значений временного ряда при изменении корреляционных сво йст в временного

ряда, а также при изменении срока прогнозирования.

Порядок выполнения работы

Задание 1. Пусть x

— процесс СС (q), определяемый разностным уравне-

нием

j=0

t−j

+ m

, (4.14)

где W

— стандартный белый шум с нормальным распределением. Задать функ-

цию m

. Задать зависимость b

от j (например, последовательност ь чисел одно-

го знака, не увеличивающихся по абсолютной величине с рост ом j). Произв ест и

имитацию процесса (

4.14).

Задание 2. По заданной выборке {x

, 1 ≤ t ≤ N} построить оценку пред-

сказания {ˆx

N+τ

, τ = 1, 2, 3}. Построить доверительные интервалы для каждой

из оценок ˆx

N+τ

, зад авш ись уровнем значимости α. Графическ и представить на

одном рисунке для некоторого диапазона N доверительные интервалы, реали-

зацию x

, оценку предсказания ˆx

N+τ

Задание 3. Вычислить матрицу корреляции Σ

εε

ошибок предсказания

{ˆx

N+τ

, τ = 1, 2, 3}. Исследовать зависимость дисперсий ошибок (ˆx

N+τ

− x

N+τ

)

и detΣ

εε

от величины q, которую в данном случае можно назвать временем кор-

реляции временного ряда (4.14). Уч есть , что корреляционная функция процесса

(4.14) вычисляется по формуле

(k) =

j=0

j+|k|

, |k| ≤ q; r

(k) = 0, |k| > q.

Задание 4. По заданной выборке {x

, 1 ≤ t ≤ N } найти оценку предсказания

ˆx

N+τ

для некоторых значений q (например, q = 1, 3, 5). Построить доверитель-

ные интервалы для каждого из вариантов при некотором уровне значимости

α. Графически представить на одном рисунке для некоторого диапазона N до-

верительные интервалы, реализацию x

и оценку предсказания ˆx

N+τ

во всех

вариантах изменения q.

Задание 5. Вычислить матрицу корреляции Σ

εε

ошибок предсказания

(ˆx

Nτ

− x

N+τ

). Исследов ать зависимость дисперсий ошибок от величины τ при

различных q.

Лабораторная работа 13. Прогнозирование значений тренда

Цель работы. Освоить технику оценивания функции регрессии с целью про-

гнозирования ее значений.

Порядок выполнения работы

Использовать временной ряд, который исследовался в лабораторной рабо-

те 12.

Задание. Определить множества значений параметра временного ряда,

в которых берутся наблюдения (T ) и в которых надо построить прогноз

(

T ). Рассматривая

T ∪ T , определить отрезок [a, b], на котором следует вос-

становить функци ю регрессии. Осуществить прогнозирование по формулам

(

4.11)—(4.13). Определить качество прогнозирования, пользуясь критерием

∆ =

t∈

|ˆm

− m

|/|

T |. Исследовать зависимость качества прогнозирован ия ∆

от объема выборки временного ряда N и от величины набора базисных функ-

ций s.

4.2. Предсказание ССП

Значения СП y

в модели (

4.1) являются ненаблюдаемыми, однако они влия-

ют на предсказываемые значения временного ряда x

. Если m

— известная

функция своего параметра или ее оценка уже получена спос обом, описанным

в гл.2, можно ввести разности x

− m

, которые и характеризуют значения СП

. Предсказывая значения y

для необходимого значения параметра t и исполь-

зуя известное или предсказанное значение m

на основе (4.1), можно получить

предсказанное значение временного ряда.

Рассмотрим проблему предсказания y

, полагая, что M{y

} = 0, а корреля-

ционная функция r(τ ) = M{y

t+τ

} этого процесса является известной. Пусть

значения СП {y

, y

, . . . , y

} известны и необходимо оценить y

N+k

, k > 0. В фор-

муле (4.4) определена оптимальная оценка прогнозируемого значения, в (4.8) она

построена для нормального р аспр ед елен ия. В частности, для случая оценива-

ния СП y

с нулевым средним и корреляционной функцией r(τ) оптимальный

прогноз (4.8) трансформируется в выражение

ˆy

N+k

= (r(N + k − 1), r(N + k − 2), . . . , r(k))R

−1

, y

, . . . , y

)

∗

= r(N + k − 1, k)R

−1

y(1, N ), (4.15)

где корреляционная (N × N )-матрица R = (R

) составлена и з элементов

= r(i − j), а структура строки r(N + k − 1, k) и столбца y(1, N) понятна

из (4.15). В представлении (4.10) эта оценка имеет нулевое среднее a и матрицу

коэффициентов регрессии, которая вырождается в строку

B = (b

, b

, . . . , b

) = r(N + k − 1, k)R

−1

. (4.16)

С учетом этого оценку предсказания для нормального ССП можно представить

в виде

ˆy

N+k

i=1

= By(1, N ), (4.17)

где коэффициенты b

определены равенством (

4.16).

Если процесс y

не является нормальным, выч исл ени е условного математи-

ческого ожидания (4.4) о бычно за труднительно. Поэтому в среднеквадратич ной

теории анализа временных рядов принято строить оценки предсказания в классе

линейных оценок. Предположим также, что выполняется обычно реализующее-

ся на практике условие

r(0) > 0, lim

τ→∞

r(τ) = 0. (4.18)

Тогда оценку предсказания будем искать в форме

ˆy

N+k

= f(y

, y

, . . . , y

) =

l=1

N,l

N−l+1

. (4.19)

Подставляя (

4.19) в (4.17) и разрешая это ура внен ие , при выполнении условия

(4.18) получаем, что коэффициенты регрессии b

N,k

оптимальной оценки пред-

сказания определяются из равенства

N,1

, b

N,2

, . . . , b

N,N

) = (r(k), r(k + 1), . . . , r(N + k − 1))R

−1

. (4.20)

Дисперсия D

(N) ошибки предсказания по формула м (4.19), (4.20) выража-

ется равенством

(N) = M{(ˆy

N+k

− y

N+k

)

} =

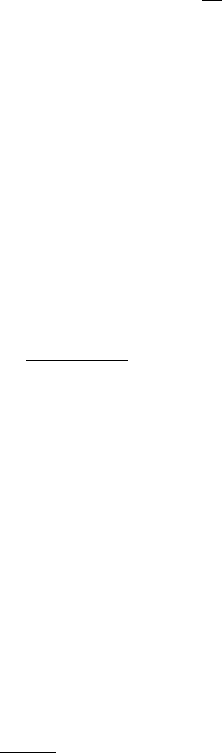
= r(0) − r(k, N + k − 1)R

−1

∗

(k, N + k − 1). (4.21)

Как видно из сравнения (4.15), (4.19) и (4.20), для нормальног о процесса y

оптимальная линейная оценка пр едс казания полностью совпадает с общей оп-

тимальной оценкой.

Часто по значениям {y

, y

, . . . , y

} необходимо предсказать следующее зна-

чение y

N+1

. Для этого случая имеет место предельный р езультат. Обозн ачим

= D

(+∞), тогда

log D

= lim

N → ∞

log detR (N ) , (4.22)

где D

— минимальная дисперсия оценки предсказания, определяющая пре-

дельную точн ост ь предсказания на один шаг; R(N) = (R

), 1 ≤ i, j ≤ N,

= r(i − j).

Между оптимальными коэффициентами регрессии (

4.20) и точностью пред-

сказания (4.21 ) для k = 1 может быть установлено взаимно однозначное соответ-

ствие, которое позволяет производить их вычисление по рекуррентным форму-

лам (метод Дурбина — Левинсона). Если выполнен о условие (4.18) и обозначено

(0) = r(0), b

1,1

= r(1)/r(0), то справедливы рекуррентные формулы

(N) = D

(N − 1)(1 − b

N,N

(N − 1)





r(N) −

N−1

j=1

N−1,j

r(N − j)





, (4.23)

N,k

= b

N−1,k

− b

N,N

N−1,N−k

, 1 ≤ k ≤ N − 1.

Иногда может оказаться более подходящим представление линейной оценки

предсказания, которое отличается от (

4.17) и для k = 1 записывается в виде

ˆy

= 0, ˆy

N+1

j=1

N,j

N+1−j

− ˆy

N+1−j

), N > 0, (4.24)

где коэффициенты θ

N,j

вычисляются рекуррентно по формулам:

N,N

= v(N + 1, 1)/v(1, 1);

N,N−k

(k)





v(N + 1, k + 1) −

k−1

j=0

k,k−j

N,N−j

(j)





;

1 ≤ k ≤ N − 1, (4.25)

(k) = v(k + 1, k + 1) −

k−1

j=0

k,k−j

(j), 1 ≤ k ≤ N,

(0) = v(1, 1).

Здесь в отличие от предыдущего обозначено M{y

} = v(i, j). Если y

—

ССП, то v(i, j) = r(i − j). По рекурр ент ным формулам (4.25) величины D

(k)

и θ

k,j

вычисляются в следующей последовательности: θ

, D

(1); θ

, θ

, D

(2);

, θ

, D

(3) и т.д.

Рекуррентные формулы Дурбина — Левинсона определяют коэффициенты

в (4.19) при прошлых значениях y

, в то время как формулы (4.25) определяют

коэффициенты при обновлениях (инновациях) (y

− ˆy

) в ортогональном раз-

ложении (4.24). Это разложение яв ляе тся очень простым при использовании.

Заметим, что если положим θ

N,0

= 1, то

N+1

j=0

N,j

N+1−j

− ˆy

N+1−j

), N = 0, 1, 2, . . . ,

т.е. текущее значение процесса y

представится в виде разложения по обновле -

ниям (y

− ˆy

). Оценка п ред сказания тип а (

4.24), (4.25) может быть получена и

для прогноза на k шагов. Она приобретает форму

ˆy

(k)

N+k

N+k−1

j=k

N+k−1,j

N+k−j

− ˆy

(1)

N+k−j

), (4.26)

где коэффициенты θ

N+k−1,j

по-прежнему вычисляются при помощи (

4.25); ˆy

(i)

—

оценка предсказания на i шагов по (N −i) наблюдениям. Средний квадрат ошиб-

ки предсказания может быть подсчитан п о формуле

(N) = M{(y

N+k−j

− ˆy

N+k−j

)

} =

= v(N + k, N + k) −

j=1

N+k−1,N +k−j

(j). (4.27)

Рассмотрим некоторые важные случаи.

Процесс АРСС (p, q) . Пусть y

— каузальный процесс АРСС (p, q). Поль-

зуясь формулами (

4.24), (4.25), можно было бы по стр оит ь пр оцес с п ред ска-

занных значений для ˆy

. Причем в этом случае каждое ˆy

t+1

определялось бы

t инновациями (y

− ˆy

). В данном случае удается построить более простой про-

цесс предсказанных значений, в котором для определения оценки ˆy

t+1

требуется

только m = max(p, q) инноваций (y

−ˆy

) независимо от t. Этот процесс строится

следующим образом. Мы предполагаем, что y

описывается уравнением

i=1

t−i

j=0

t−j

, (4.28)

где a

, b

— известные константы; W

— процесс белого шума. Тогда

ˆy

N+1

j=1

N,j

N+1−j

− ˆy

N+1−j

), 1 ≤ N < m,

ˆy

N+1

i=1

N+1−i

j=1

N,j

N+1−j

− ˆy

N+1−j

), N ≥ m. (4.29)

Причем D

(N) = M{(y

N+1−j

− ˆy

N+1−j

)

} = σ

(N). Величины D

(N) и

N,j

определяются формулами (4.25), в которых D

(k) необходимо заменить на

(k), а v(i, j) вычислить следующим образом:

v(i, j) =











r(i − j)/σ

, 1 ≤ i, j ≤ m;

r(i − j) −

k=1

r(k − |i − j|)

, min(i, j) ≤ m,

m ≤ max(i, j) ≤ 2m;

k=0

k+|i−j|

, min(i, j) > m;

0, в остальных случаях.

(4.30)

Заметим, что если v(i, j) определяется соотношением (

4.30), а в (4.25) вместо

(k) используется D

(k) = D

(k)/σ

, то D

(k) и θ

i,j

, определяемые формулами

(4.25), не зависят от σ

. В (4.30) r(τ) — функция ковариации процесса (4.28);

— дисперсия белого шума W

. Напомним, что функция ковариации процесса

(4.28) имеет вид

r(τ) = σ

∞

j=0

j+|τ |

, τ = 0, ±1, ±2, . . . , (4.31)

где значения ψ

могут быть вычисле ны рекуррентно (предполагается, что

= 1, a

= 0 для i > p; b

= 0 для j > q) по формулам

= 1;

= b

k−1

i=0

k−i

, 1 ≤ k < max(p, q + 1), (4.32)

k−1

i=k−p

k−i

i=1

k−i

, k ≥ max(p, q + 1).

Таким образом, для построения процесса, предс казывающего временной ряд

типа АРСС (p, q) на один шаг вперед, можно воспользоваться либо формулами

(

4.24), (4.25) и (4.31), (4.32) (с учетом того, что в этом случае v(i, j) =

= r(i − j)/σ

), либо формулами (4.29)—(4.32).

Заметим, что в рассматриваемом случае, если процесс АРСС (p, q) является

не только каузальным, но и обрат имым, при N → ∞ в (4.29) D

(N) → σ

N,j

→ b

, 1 ≤ j ≤ q.

Процесс АР (p). Пусть y

— процесс АР (p), который получается из (4.28),

если положить b

= 0, 1 ≤ j ≤ q. Тогда

ˆy

N+1

i=1

N+1−i

, N ≥ p, (4.33)

т.е. в оценке (

4.29) θ

N,j

= 0, 1 ≤ j ≤ q. Пусть теперь y

— процесс СС (q),

который получается из (4.28), если положить a

= 0, 1 ≤ i ≤ p. В этом случае

ˆy

N+1

min(N,q)

j=1

N,j

N+1−j

− ˆy

N+1−j

), N ≥ 1. (4.34)

Коэффициенты θ

N,j

находятся из (

4.25), где ковариации v(i, j) вычисляются по

формулам

v(i, j) =

q−|i−j|

k=0

k+|i−j|

, v(i, j) = 0, |i − j| > q. (4.3 5)

Процесс АРСС (1,1). Пусть y

— процесс АРСС (1,1). В этом случае y

t−1

+ W

+ bW

t−1

, |a| < 1. Уравнение оценки предсказания имеет вид

ˆy

N+1

= ay

+ θ

− ˆy

), N ≥ 1. (4.36)

Используя (

4.31), (4.32) и (4.30), получаем

v(i, j) =











(1 + 2ab + b

)/(1 − a

), i = j = 1,

(1 + b

), i = j ≥ 2,

b, |i − j| = 1, i ≥ 1,

0, в остальных случаях,

а из (

4.25) с учетом этого равенства

N,1

= b/D

(N − 1), D

(N) = (1 + b

− (b/D

(N − 1))).

Описанные результаты можно обобщить на случай предсказания на k шагов

вперед процесса АРСС (p, q). Тогда оценка пр едс казания для процесса (4.28)

ˆy

(k)

N+k

i=1

ˆy

(k−i)

N+k−i

j=k

N+k−1,j

N+k−j

− ˆy

(1)

N+k−j

), (4.37)

где второе слагаемое обращается в нуль при k > q.

Среднее значение квадрата ошибки предсказания по (

4.37) выражается фор-

мулой