Медведев Г.А., Морозов В.А. Практикум на ЭВМ по анализу временных рядов
Подождите немного. Документ загружается.

асимптотическое ра спр еде лен ие позволяет получить приближенные доверитель-
ные интервалы для оцененных коэффициентов:
{θ
j
∈ R : |θ
j
−
ˆ
θ
j
| ≤ N
−1/2
Φ
−1
1−α/2
v
1/2
jj
(
ˆ
θ)}, (3.60)
где v
jj
(
ˆ
θ) — j-й диагональный элемент матрицы V (
ˆ
θ),
ˆ
θ = (
ˆ
a,
ˆ
b).
Рекуррентный МНК. Если бы в каждый момент времени t величины
W
1
, . . . , W
t
процесса АРСС (p, q) были известны, то для оц енк и параметров
ˆ
a,
ˆ
b
можно было бы применить МНК-оценки
N
X
t=1
(x
t
− Φ
∗
t−1
θ)
2
→ min
θ
,
θ = (a
1
, . . . , a
p
, b
1
, . . . , b
q
)
∗
, Φ
∗
t−1
= (x
t−1
. . . x
t−p
W
t−1
. . . W
t−q
).
Рекуррентная форма данного алгоритма аналогична (
3.14)—(3.16):
ˆ
θ(t + 1) =
ˆ
θ(t) − P (t)Φ
t
L
t
(x
t+1
− Φ
∗
t
ˆ
θ(t)); (3.61)
P (t + 1) = P (t) − P (t)Φ
t+1
L
t+1
Φ
∗
t+1
P (t); (3.62)
L
t+1
= (1 + Φ
∗
t+1
P (t)Φ
t+1
)
−1
. (3.63)
Использование в этом алгоритме вместо неизвестных СВ W
1
, . . . , W
t
подходящих
оценок
˜
W
1
, . . . ,
˜
W
t
делает процедуру оценивания реализуемой. Оценку
˜
W
t
можно
интерпретировать как прогноз СВ W
t
по данным наблюдениям
ˆ
θ(1), . . . ,
ˆ
θ(t),
˜
W
1
, . . . ,
˜
W
t−1
, x
1
, . . . , x
t
. Будем вычислять
˜
W
t
следующим образом:
˜
W
t
= x
t
− Φ
∗
t−1
ˆ
θ(t). (3.64)
Соотношения (
3.61)—(3.64) после задания начальных оценок θ(0), P (0),
˜
W
0
,
˜
W
−1
, . . . полностью определяет рекуррентную процедуру оценивания. Рекур-
рентная процедура МНК становится малопригодной, ес ли приходится оценивать
вектор параметров высокой размерности: основной объем выч и слен ий связан с
процедурой вычисления матриц P (t). Предложим упрощенный вариант МНК,
когда в алгоритме оценивания исп ол ьзуется не сама матрица P (t), а ее след.
Алгоритм имеет вид
ˆ
θ(t + 1) =
ˆ
θ(t) − L
t
P
t−1
Φ
t
(x
t+1
− Φ
∗
t
ˆ
θ(t)); (3.65)
p
−1
t+1
= p
−1
t
+ Φ
∗
t+1
Φ
t+1
; (3.66)
L
t
= (1 + p
t−1
Φ
∗
t
Φ
t
)
−1
. (3.67)
Данный алгоритм является одним из вариан тов метода стохастической ап-
проксимации.
Метод оценивания параметров АРСС с пропущенными наблюде-
ниями. Пусть каузальный и обрат имый процесс АРСС описывается уравнени-
ем (
3.1). Предположим, что можно наблюдать не все величины x
1
, x
2
, . . . , x
N
.
80

Пусть, например, известны r наблюдений x
j
1
, . . . , x
j
r
. Для того, чтобы вычис-
лить логарифмическую функцию правдоподобия, надо искусственно добавить
ряд наблюдений до числа N следующим образом. Перепишем уравнение АРСС
в виде Y
t+1
= F Y
t
+ T W
t+1
; x
t
= GY
t
, t = 1, 2, . . ., где i-я компонента вектора
Y
t
, i = 1, . . . , k = max(p, q + 1), определяется уравнением
(Y
t
)
i
=
k
X
j=i
(a
j
x
t+i−1−j
+ b
j−1
W
t+i−j
), i = 1, . . . , k;
a
j
= 0 для j > k и b
j
= 0 для j > q; F = ||f
ij
||, f
ij
= a
1
δ
ij
+ δ
i+1,j
, δ
ij
— символ
Кронекера, i, j = 1, . . . , k; T = (1 b
1
. . . b
k−1
)
∗
, G = (1 0 . . . 0).
Определим величину z
t
= G
t
Y
t
+ α
t
V
t
, t = 1, 2, . . . , где {V
t
} — последователь-
ность независ имых гауссовских СВ с нулевым средним и единичной дисперсией,
не зависит от Y
1
, W
2
, W
3
, . . . и
G
t
=
½
0, если x
t
пропущено
G, иначе
α
t
=
½
1, если x
t
пропущено
0, иначе.
Таким образом, вектор Z
N
= (z
1
. . . z
N
)
∗
совпадает с x
N
1
, за исключением
ненаблюдаемых компонент x
N
1
, которые в Z
N
заменяются независимыми стан-
дартными гауссовскими величинами. Тогда одношаговый прогноз величины ˆz
j
,
j = 1, . . . , N , получается с помощь ю алгорит ма калмановской фил ьтрации:
ˆ
Y
t+1
= F
˜
Y
t
; (3.68)
Σ
t+1
= F
˜
Σ
t
F
∗
+ T T
∗
; (3.69)
ˆz
t
= G
t+1
ˆ
Y
t+1
; (3.70)
s
t+1
= G
t+1
Σ
t+1
G
∗
t+1
+ α
2
t+1
; (3.71)
K
t+1
= Σ
t+1
G
∗
t+1
/s
t+1
; (3.72)
˜
Y
t+1
=
ˆ
Y
t+1
+ K
t+1
(z
t+1
− ˆz
t+1
); (3.73)
˜
Σ
t+1
= Σ
t+1
− K
t+1
G
t+1
Σ
t+1
, (3.74)
с начальными условиями
ˆ
Y
1
= 0, Σ
1
= M{Y
1
Y
∗
1
}, ˆz
1
= 0,
s
1
= α
2
1
+ σ
2
x
, K
1
= s
−1
1
Σ
1
G
∗
,
˜
Y
1
= K
1
z
1
,
˜
Σ
1
= Σ
1
− K
1
GΣ
1
, σ
2
x
= M{x
2
t
}.
Логарифмическая функция правдоподобия имеет вид
L
N
(a, b, σ
2
, x
N
1
) = −
1
2
·
rln (2πσ
2
) +
X
0
ln s
i−1
+
1
σ
2
X
0
(x
i
− ˆz
i
)
2
/s
i−1
¸
,
где
0
у суммы означает суммирование только по тем индексам i, для которых x
i
наблюдается; s
i
, ˆz
i
определяются по формулам (
3.68)—(3.74). Поиск неизвестных
параметров осуществляется с помощью алгоритмов нелинейной оптимизации.
81
Лабораторная работа 10. Оценивание параметров процесса АРСС
(p, q)
Цель работы. Познакомиться с методами оценивания коэффициентов про-
цесса АРСС и дисперсии шума, освоить их и провести сравнительный анализ
алгоритмов.
Порядок выполнения работы
Используя генераторы псевдослучайных чисел, пр оиз вес ти моделирование
временных рядов, порождаемых каузальн ым и обратимым процессом АРСС
(p, q).
Задание 1. Оцени ть коэффициенты процесса АРСС (p, q) с помощью метода
Юла — Уолкера (алгоритмы 1–3). Провести сравнительный анализ по эффек-
тивности и точности оценок коэффициентов, входящих в уравнение скользящего
среднего.
Задание 2. Оцени ть коэффициенты процесса АРСС (p, q) с помощью метода
Дурбина — Левинсона. Провести сравнительный анализ по эффективности и
точности оценок коэффициентов с оценками из задания 1.
Задание 3. Оценить коэффициенты процесса АРСС (p, q) с помощью мето-
да максимального правдоподобия (алгоритм Бокса — Дженкинса и алгоритм,
основанный на прогнозе). Провести сравнительный анализ по эффективности и
точности предложенных алгоритмов. Для алгоритма Бокса — Дженкинса подо-
брать оп тимал ьн ые значения T и M . Для поиска экстремума функции F
N
и S
N
использовать градиентные прямые методы, а также методы случайного поиска.
Задание 4. Оценить ковариационную матрицу оцен ки ММП (формулы
(
3.57)—(3.59)). Построить доверительные интервалы для коэффициентов по
формуле (3.60) . Исследовать зависимость качества оценок (величины довери-
тельных интервалов) от значений коэффициентов процесса АРСС. Изобразить
графически поведение оценок ММП и доверительные границы.
Задание 5. Оценить коэффициенты процесса АРСС (p, q) с помощью ре-
куррентного алгоритма МНК (формулы (3.61)—(3.63)) и упрощенного варианта
(формулы (3.65)—(3.67)). Исследовать эффективность алгоритмов для оценива-
ния коэффициентов процесса АРСС. Используя рекуррентные алгоритмы МНК,
оценить коэффициенты процесса АРСС с трендом (3.41).
Задание 6. Оценить коэффициенты процесса АРСС (p, q) для модели с про-
пущенными наблюдениями. В качестве модели пропуска наблюдений использо-
вать модель пропуска через фиксированное или случайное число тактов вре-
мени. Исследовать в ли яни я числа m = N − r пропущенных наблюдений на
точность оценивания.
3.4. Обнаружение разладки процессов АРСС
Пусть {x
k
, 1 ≤ k ≤ t} = x
t
1
— реализация СП x
t
, которая в момент t
0
скачко-
образно меняет свои свойства. В общем случае это означает, что до момента t
0
82

процесс x
t
имел распределение F
0
(x
1
, . . . , x
t
0
), а после этого момента — распре-
деление F
1
(x
t
0
+1
, . . . , x
N
). С практической точки зрения существует два типа
задач, решаемых с помощью алгоритмов обнаружения разладки . В первом слу-
чае необходимо обнаруживать разладку как можно быстрее после ее появления
при заданном уров не ложных тревог и определить момент времени, когда про-
изошла разладка. Алгоритмы подо бно го типа называются последовательными
алгоритмами обнаружения разладки. Второй осно вно й тип за дач сводится к
оцениванию момента появления разладки после получения всей выборки.
В некоторых случаях сам факт наличия разладки в пр еде лах анализируемой
выборки заранее неизвестен, и проверка ее наличия также является предметом
решения. Алгоритмы подобного типа называются алгоритмами апостериорного
обнаружения разладки.
Будем рассматривать параметрические свойства распределений F
0
, F
1
, в
частности, процессы АРСС.
Апостериорные алгоритмы. Пусть две части временного ряда x
t
0
−1
1
и x
N
t
0
порождаются стационарными моделями АР (p) и x
t
0
−1
1
не зависит от x
N
t
0
, т.е.
x
t
=
p
X
i=1
a
(j)
i
x
t−i
+ W
t
, (3.75)
где a
(j)
1
, . . . , a
(j)
p
— коэффициенты АР до (j = 1) и пос ле (j = 2) разладки;
σ
2
j
— дисперсия независимой по сле дов ател ьн ости W
t
, M{W
t
} = 0, M{W
2
t
} =
= σ
2
j
. Если векторные параметры θ
∗
j
= (a
(j)
1
. . . a
(j)
p
σ
2
j
), j = 1, 2, известны, то для
определения момента t
0
можно использовать ММП:
t
0
= arg max
p + 1 ≤ k ≤ N − p
[lnp(x
k−1
1
|θ
1
) + lnp(x
N
k
|θ
2
)] =
= arg max
p + 1 ≤ k ≤ N − p
h
lnp(x
p
1
|θ
1
) +
k−1
X
t=p+1
lnp(x
t
|x
t−1
t−p
, θ
1
)+ (3.76)
+lnp(x
k+p−1
k
|θ
2
) +
N
X
t=k+p
lnp(x
t
|x
t−1
t−p
, θ
2
)
i
,
где p(·|·) — условная плотность. Рассмотрим случай гауссовской модели, т.е.
W
t
∼ N(0, σ
2
j
), и предположим, что N À p. Тогда (
3.76) можно аппроксимиро-
вать следующим образом:
t
0
= arg max
p + 1 ≤ k ≤ N − p
h
−
k
2
ln(2πσ
2
1
) −
1
2σ
2
1
k
X
t=p+1
e
2
t1
−
−
n − k
2
ln(2πσ
2
2
) −
1
2σ
2
2
N
X
t=k+1
e
2
t2
i
, (3.77)
83

e
2
tj
=
Ã
x
t
−
p
X
i=1
a
(j)
i
x
t−i
!
2
, j = 1, 2.
Если θ
1
и θ
2
неизвестны, то в (
3.77) испо льз уются оценки
ˆ
θ
1
,
ˆ
θ
2
. Оценки
ˆ
θ
1
рассчитываются по значениям выборки x
k
1
, а
ˆ
θ
2
— по значениям x
N
k
, в то время
как k изменяется от p + 3 до N − p − 1.
В рамках данного подхода можно исследова ть модель разладки авторегрес-
сии для случая, когда п осле дов ате льн ости x
t
0
−1
1
и x
N
t
0
зависимы. Первую модель
разладки можно рассматривать как момент переключения с наблюдения гене-
ратора авторегрессионной последовательности (
3.75) с параметрами θ
1
на на-
блюдение генератора с параметрами θ
2
. Вторая модель разла дки соответствует
не переключению наблюдения, а скачкообразному изменению коэффициентов
генератора (3.75) с сохранением ”хвоста” памяти x
t
0
−1
t
0
. Для новой модели раз-
ладки соотношение (3.76) заменяется на следующее:
t
0
= arg max
p + 1 ≤ k ≤ N − p
ln
p(x
k−1
1
|θ
1
)
p(x
N
k
|θ
2
)
,
где θ
1
, θ
2
известны.
В случае гауссовской АР данный алгоритм имеет вид
t
0
= arg max
p + 1 ≤ k ≤ N − p
−k ln
σ
1
σ
2
+
1
2σ
2
2
k
X
t=p+1
e
2
t2
−
1
2σ
2
1
k
X
t=p+1
e
2
t1
. (3.78)
Для от ыскания неизвестных параметров можно использовать метод Юла — Уо-
лкера или рекуррентный МНК.
Последовательные алгоритмы. Существуют два подхода для обнаруже-
ния разладки. Первый состоит в пропускании наблюдаемого сигнала x
t
через
выбеливающий фильтр и в проверке отклонения характеристик последов ател ь-
ности остатков e
t
данного фильтра от параметров белого шума. Будем называть
его одномодельным. Второй подход основан на использовании двух моделей, ко-
торые оцениваются на различных участках временного ряда и сравниваются
между собой с помощью подходящей меры расстояния между р аспределени-
ями. Будем называть его двухмодельным. Существуют также два алгоритма
оценивания момента изменения свойств t
0
.
Алгоритм 1. Данный алгоритм основан на использовании порогового реша-
ющего правила для статистик, представленных в виде кумулятивных сумм:
S
t
=
t
X
k=1
s
k
, (3.79)
где s
k
— некоторая статистика. Статистика s
k
подбирается таким образом, чтобы
до разладки S
t
в среднем дрейфовала вниз, а после разладки — вверх . При этом
правило подачи сигнала о разладке имеет вид
t
0
= inf{t ≥ 1 : g
t
≥ h}, (3.80)
84
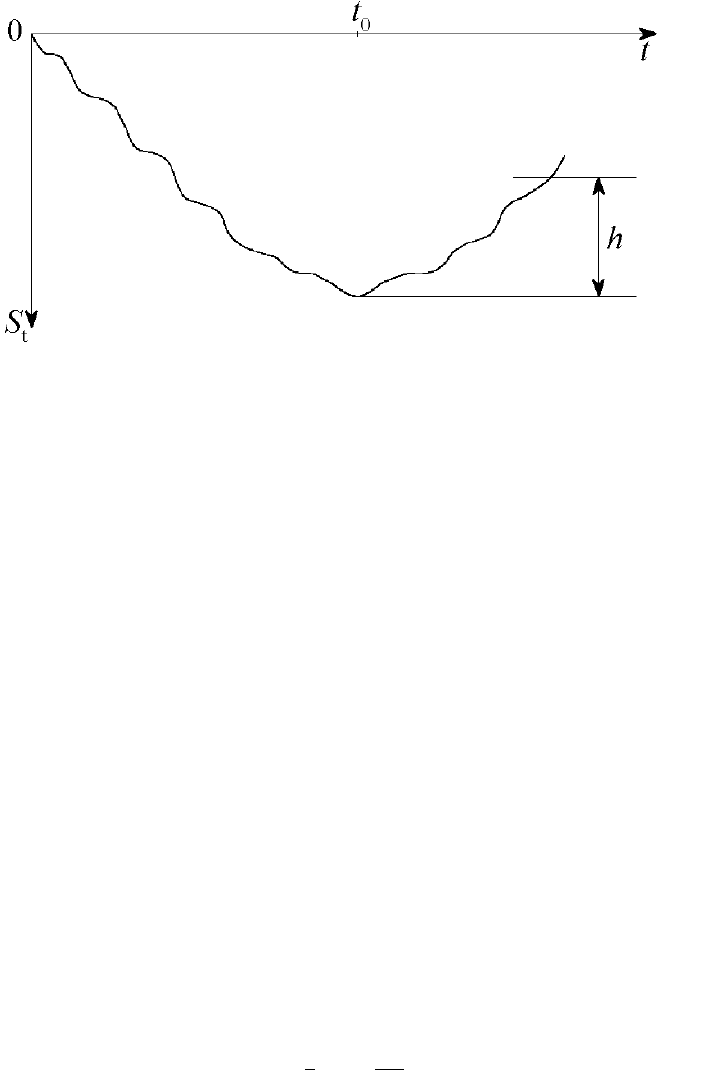
где g
t
= S
t
− min
1 ≤ k ≤ t
S
k
; h > 0 — порог. Поведение суммы S
t
до и после
разладки изображено на рис. 3.1.
Рис. 3.1
Опишем алгоритмы обнаружения разладки временного ряда, порождаемого
процессом АР (p). Все алгоритмы осно ван ы на статистиках вида (3.79). Рас-
смотрим идеальный случай, когда парамет ры АР (p) известны до и после изме-
нения свойств. Пусть СП x
t
описывается известными условными плотностями
p
1
(x
t
|x
t−1
1
) = p(x
t
|x
t−1
1
, θ
1
) до изменения и p
2
(x
t
|x
t−1
1
) = p(x
t
|x
t−1
1
, θ
2
) — после
изменения.
Одномодельный подход для обнаружения разладки использует статистику
U
t
=
t
X
k=1
u
k
, (3.81)
где
u
k
=
Z
p
1
(x |x
k−1
1
)lnp
1
(x |x
k−1
1
) dx − lnp
1
(x |x
k−1
1
).
Статистика U
t
до изменения имеет нулевое среднее и принимает положительное
значение после изменения, если выполняется условие
H
x
t
(p
2
) > H
x
t
(p
1
), (3.82)
где H
x
t
(p
j
), j = 1, 2 — условная энтропия: H
x
t
(p
j
) = −
R
p
j
(x |x
k−1
1
)×
×lnp
j
(x |x
k−1
1
) dx.
В гауссовском случае для модели АР (p) статистика U
t
принимает вид
U
t
=
1
2
t
X
k=1
µ
e
2
k1
σ
2
1
− 1
¶
. (3.83)
85

Условие (3.82) изменяется следующим образом: σ
2
> σ
1
. Если же σ
2
< σ
1
, то по-
сле изменения среднее статистики U
t
может быть положительным, отрицатель-
ным или даже нулевым. В этом случае не рекомендуется использовать тест U
t
.
При применении двухмодельного подхода можно использовать три статисти-
ки.
1. Статистика, основанная на отношении правдоподобия:
V
t
=
t
X
k=1
v
k
,
где v
k
= ln[p
2
(x
k
|x
k−1
1
)/p
1
(x
k
|x
k−1
1
)].
2. Статистика, основанная на расстоянии между условными распределения-
ми, определяемом дивергенцией Кульбака:
D
t
=
t
X
k=1
d
k
,
где
d
k
= −
Z
p
1
(x |x
k−1
1
)ln
p
2
(x |x
k−1
1
)
p
1
(x |x
k−1
1
)
dx + ln
p
2
(x
k
|x
k−1
1
)
p
1
(x
k
|x
k−1
1
)
=
= −I
x
k
(p
2
|p
1
) + ln
p
2
(x
k
|x
k−1
1
)
p
1
(x
k
|x
k−1
1
)
,
где I
x
k
(p
2
|p
1
) — информационное число Кульбака. Условные математические
ожидания этих двух статистик V
t
и D
t
до изменения и после него имеют вид
M
1
{v
t
|x
t−1
1
} = −I
x
k
(p
1
|p
2
) < 0,
M
1
{d
t
|x
t−1
1
} = 0,
M
2
{v
t
|x
t−1
1
} = I
x
k
(p
2
|p
1
) > 0,
M
2
{d
t
|x
t−1
1
} = J(p
1
, p
2
) > 0,
где M
j
{·|·} — математическое ожидание по распредел ени ю p
j
(·|·); J(p
1
, p
2
) —
дивергенция Кульбака между условными плотностями.
3. Статистика, основанная на расстоянии Чернова между условными распре-
делениями:
Z
t
=
t
X
k=1
z
k
,
где приращения z
k
таковы, что
M
1
{z
k
|x
k−1
1
} = const,
M
2
{z
k
|x
t−1
1
} = f
k
(τ) = ln
Z
[p
2
(x |x
k−1
1
)]
τ
[p
1
(x
k
|x
k−1
1
)]
1−τ
dx,
86
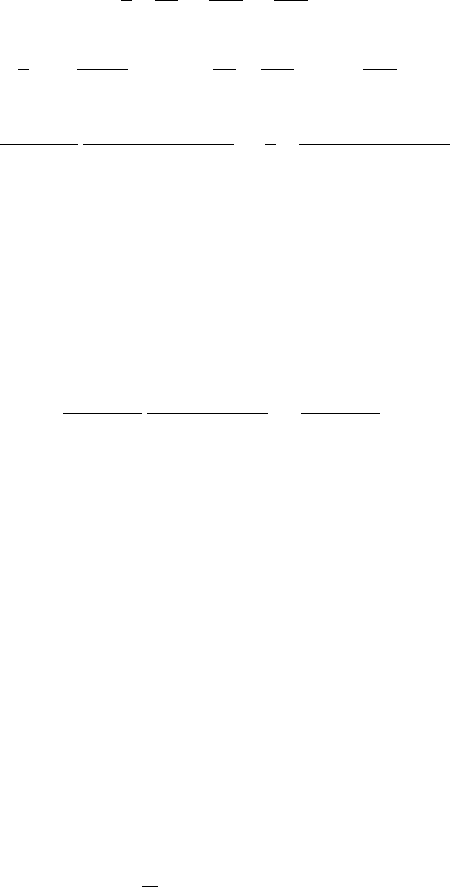
где f
k
(τ) — расстояние Чернова между условными плотностями p
1
, p
2
,
0 < τ < 1.
Теперь рассмотрим случай гауссовской АР. Запишем статистики v
t
, d
t
, z
t
сле-
дующим образом:
v
t
=
1
2
ln
σ
2
1
σ
2
2
+
e
2
t1
2σ
2
1
−
e
2
t2
2σ
2
2
; (3.84)
d
t
=
1
2
·
−2
e
2
t1
e
2
t2
2σ
2
2
+
µ
1 +
σ
2
1
σ
2
2
¶
e
2
t1
2σ
2
1
− 1 +
σ
2
1
2σ
2
2
¸
; (3.85)
z
t
= z
t
(τ) =
τ(τ − 1)
2
e
t1
(e
t1
− e
t2
)
τσ
2
2
+ (1 − τ)σ
2
1
−
1
2
ln
σ
2τ
2
σ
2(1−τ)
1
τσ
2
2
+ (1 − τ)σ
2
1
, (3.86)
где e
tj
, j = 1, 2, определяются формулой (
3.77).
В частном случае, когда коэффициенты АР не изменяются (т.е. e
t1
= e
t2
), а
изменяется только дисперсия, формула (3.86) задается соотношением
2z
t
(τ) = ln(τσ
2
2
+ (1 − τ)σ
2
1
) − τlnσ
2
2
− (1 − τ)lnσ
2
1
. (3.87)
В случае, когда дисперсия остается постоянной (т.е. σ
1
= σ
2
), статистика при-
нимает вид
z
t
(τ) =
τ(τ − 1)
2
e
t1
(e
t1
− e
t2
)
σ
2
=
τ(τ − 1)
2
d
t
.
На практике модели АР до и после изменения неизвестны и должны быть
идентифицированы. При использовании единственной модели, т.е. когда разлад-
ку определяют с помощью U
t
, АР-модель идентифицируют (оценивают парамет-
ры a
1
, . . . , a
p
, σ
2
, p с помощью рекуррентных алгоритмов (например, МНК).
При испол ьзо ван ии двухмодельного подхода необходимо выбрать располо-
жение двух участков временного ряда для идентификации моделей. Первую
АР-модель M
1
идентифицируют в фиксированном окне (например, T значений
в начале временного ряда) и используют ее в качестве проверяемой модели. Дру-
гими словами, взяв значения x
t
1
, . . . , x
t
1
+T
, оценивают параметры АР-модели
a
(1)
1
, . . . , a
(1)
p
, σ
2
1
. Затем вторую модель M
2
идентифицируют в скользящем окне
такого же размера и применяют в качестве проверяемой модели (т.е. оценивают
коэффициенты a
(2)
1
, . . . , a
(2)
p
, σ
2
2
). Когда модели суще ств енн о отличаются друг
от друга, находят момент разладки, вто рая модель становится первой и т.д. В
качестве меры различия двух моделей можно использовать статистику
f
T
=
1
T
T
X
t=1
(e
t1
− e
t2
)
2
,
где обновляющие последовательности e
t1
и e
t2
определяются на окнах M
1
и M
2
соответственно. Этот способ имеет недостаток, заключающийся в возр астании
вероятности ложной тревоги. Об эт ом свидетельствует простой факт: вслед-
ствие иденти фикации опорной модели M
1
внутри временн ого окна заведомо
87
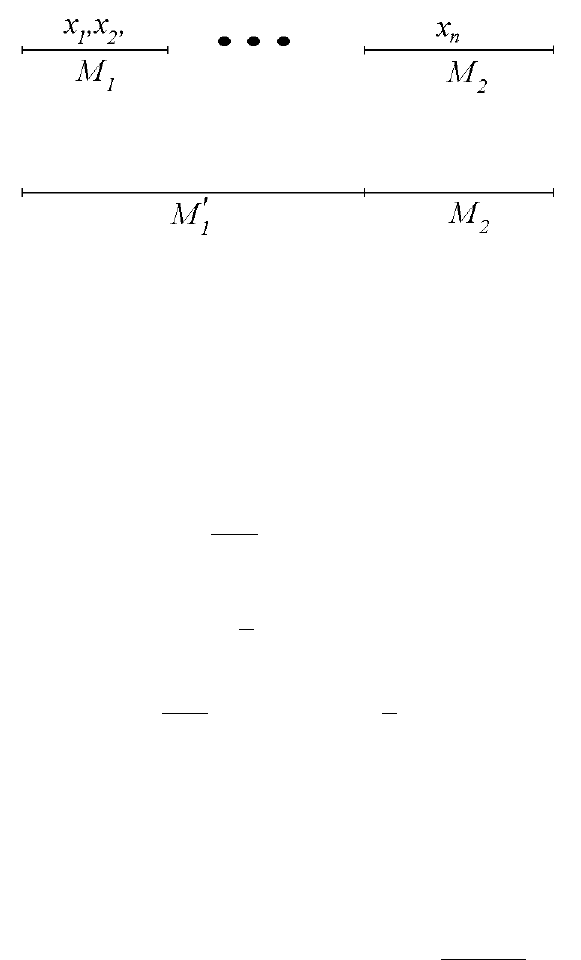
ограниченных размеров часть информации о сигнале до изменения теряется.
Положение можно изменить к лучшему, если в качестве опорной исп оль зов ать
глобальную (т.е. оцененную в длинном в ремен ном окне) модель M
0
1
вместо ло-
кальной (т.е. оцененной в коротком временном окне) модели (рис. 3.2).
Рис. 3.2
В общем случае, значения x
t
1
, . . . , x
t
1
+t−k
определяют окно M
0
1
, а значения
x
t
, . . . , x
t+T
— окно M
2
(t — текущее время). Если t
1
= 1, k = 0, окна M
0
1
, M
2
соответствуют окнам, изображенном на рис. 3.2.
Алгоритм 2. Пусть T — длина временного окна M
2
и пусть ˆσ
2
1
и ˆσ
2
2
— оце-
ненные дисперсии остатков моделей M
0
1
и M
2
соответственно:
ˆσ
2
1
=
1
t − k
t
1
+t−k
X
i=t
1
(ˆe
i1
− ¯e
1
)
2
,
ˆσ
2
2
=
1
T
t+T
X
i=t
(ˆe
i2
− ¯e
2
)
2
,
¯e
1
=
1
t − k
t
1
+t−k
X
i=t
1
ˆe
i1
, ¯e
2
=
1
T
t+T
X
i=t
ˆe
i2
,
ˆe
i1
= x
i
−
p
X
j=1
ˆa
(1)
j
x
i−j
, ˆe
i2
= x
i
−
p
X
j=1
ˆa
(2)
j
x
i−j
,
где t — текущее время; ˆa
(1)
j
, ˆa
(2)
j
— коэффициенты АР-модели, оцененные в ок нах
M
0
1
и M
2
соответственно. Тогда статистика обнаружения задается формулой
(
3.86), в которой τ = T/t, и ее можно записать в виде z
t
(T ) = = H(1, t) −
H(1, t − T ) − H(t − T + 1, t), где H(a, b) = (b − a + 1)ln
ˆσ
2
[a, b]
b − a + 1
.
Пусть также обнаружение произошло в момент времени t
∗
и истинный мо-
мент изменения находится в интервале [t
∗
−T +1, t
∗
]. Тогда вычисляются разно-
сти для момен тов t от t
∗
+ 1 до t
∗
+ T −1 по формуле ∆
t
= Z
t
(T ) −Z
t
(t −
˜
t
0
+ 1),
88
где
˜
t
0
= t
∗
− T + 1, и оценивается момент изменения
ˆ
t
0
= t
M
− T + 1, t
M
= inf{t
∗
+ 1 ≤ t ≤ t
∗
+ T − 1 : ∆
t
> 0}. (3.88)
Лабораторная работа 11. Обнаружение разладки процессов АР (p)
Цель работы. Познакомиться и освоить методы обнаружения разладки и
оценивания моментов изменения свойств процессов АР (p). Провести сравни-
тельный анализ алгоритмов.
Порядок выполнения работы
Используя генераторы псевдослучайных чисел, пр оиз вес ти моделирование
временных рядов, порождаемых процессом АР (p). В некоторые моменты вре-
мени (детерминированные или случайные) процесс АР (p) меняет свои свойства
(коэффициенты, математическое ожидание или дисперсию шума). Следует учи-
тывать, что участки стационарности или однородности (про цесс не меняет свои
свойства) должны быть достаточно большими.
Задание 1. Произвести моделирование временного ряда, порождаемого про-
цессом АР (p), с одним моментом разладки и первой моделью разладки . С по-
мощью ММП (
3.77) оценить момент разладки. Используя ММП (3.78), оценить
единственный момент разладки для второй модели. Исследовать качество алго-
ритмов в зависимости от величины разладки ∆ = ||a
(1)
− a
(2)
||.
Задание 2. Произвести моделирование временного ряда, порождаемого про-
цессом АР (p), с несколькими моментами р азл адк и. В качестве разладки ис-
пользовать изменение только коэффициенов a
1
, . . . , a
p
, только дисперсии σ
2
и
коэффициентов и дисперсии одновременно. Предположить, что параметры до
и после разладки известны точно. Оценить моменты разладки, используя ста-
тистики U
t
, V
t
, D
t
, Z
t
(τ), правила остановки (3.80) и правила остановки (3.88).
Исследовать качество предложенных методов в зависимости от величины ”скач-
ка параметров” ∆ = ||
ˆ
θ − θ||
2
, θ = (a, σ
2
).
Задание 3. Оценить моменты разладки временных рядов аналогично зада-
нию 2. При этом пред по ложить, что параметры до и после разлад к и неизвестны.
Параметры оценить с помощью метода Дурбина — Левинсона (включая порядок
p). Для оценивания использовать окн а фиксированной длины в первом случае.
Во втором случае оп ор ную модель оценивать в увеличивающемся окне. Иссле-
довать качество алго рит мов в зависимости от выбора длины фиксированного
окна T (в первом случае), величины смещения k, длины T (во втором случае) и
величины ”скачка параметров” ∆.
Задание 4. Для каждого из последовательных алгоритмов исследовать пра-
вило остановки (3.80) в зависимости от выбора п оро га h. Оценить среднюю ве-
личину запаздывания при обнаружении разладки. Для этого провести модели-
рование n временных рядов с единственной разладкой, в один и тот же момент
89
