Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.


862 VIe. Applications: Nuclear Heat Generation
Table VIe.3.1. Flux and geometrical buckling for various critical core geometries
where H is the total height of the core, as shown in Figure VIe.3.1. Reactor cores
consist of thousands of fuel rods. To be able to apply Equation VIe.3.2 to reac-
tors, we relate
Σ
f
for the entire core to that of the fuel rods by:
[(
π
a
2
H)N
rod
]Σ
fr
=
π
R
2
HΣ
f
where N
rod
is the number of fuel rods in the core. Solving for Σ
f
, we find:
Σ
f
= [a
2
N
rod
]Σ
fr
/ R
2
.
where a is the fuel rod radius. Substituting
aF
Σ in Equation VIe.3.1.2, we get:
φ
(r, z) =
¸
¸
¹
·
¨
¨
©
§
Σ
2
2
V
63.3
aNE
RQ
rodfrR
J
o
¸
¹
·
¨
©
§
R
r405.2
cos
¸
¹
·
¨
©
§
H
π
=
¸
¸
¹
·
¨
¨
©
§
Σ H
16.1
2
aNE
Q
rodfrR
J
o
¸
¹
·
¨
©
§
R
r405.2
cos
¸
¹
·
¨
©
§
H
z
π
Multiplying
φ
(r, z) by energy deposited per fission (E
d
) and substitute from Equa-
tion VIe.1.5, we obtain:
q
′′′
(r, z) =
¸
¸
¹
·
¨
¨
©
§
H
16.1
2
aNE
QE
rodR
d
J
o
¸
¹
·
¨
©
§
R
r405.2
cos
¸
¹
·
¨
©
§
H
z
π
VIe.3.3
Equation VIe.3.3 gives the distribution of the volumetric heat generation rate in
reactor cores of finite cylinder. Since [J
0
(x)]
max
= 1 and [cos(x)]
max
= 1, the maxi-
mum volumetric heat generation rate occurs at the center of the cylinder where r =
z = 0. Hence, Equation VIe.3.3 can be expressed as:

3. Determination of Neutron Flux in an Infinite Cylindrical Core 863
q
′′′
(r, z) =
max
q
′′′
J
o
¸
¹
·
¨
©
§
R
r405.2
cos
¸
¹
·
¨
©
§
H
z
π
VIe.3.4
Example VIe.3.1. A reactor core contains 41,000 fuel rods. The nuclear plant is
operating at 1000 MWe and 29% thermal efficiency. Fuel pellet diameter is 0.44
in. Core dimensions are, D = H = 4 m. Find the volumetric heat generation rate at
z = H/3 and r = R/2.
Solution: We find the maximum volumetric heat generation rate occurring at z =
r = 0 from:
max
q
′′′
= =
×××
××
=
¸
¸
¹
·
¨
¨
©
§
4]12/)2/44.0[(41000200
%)29/1000(18016.1
H
16.1
22
aNE
QE
rodR
d
65.31 MW/ft
3
= 2.23E8 Btu/h·ft
3
Therefore,
q
′′′
(r, z) = 2.23E8 [J
0
(2.405 × R/2R) cos(
π
× H/3H)] = 2.23E8 × 0.67
× 0.5 = 0.75E8 Btu/h·ft
3
.
Actual versus bare reactor cores. In actual reactor cores the maximum volu-
metric heat generation rate, is less than that calculated in the above example. To
find
max
q
′′′
in actual cores, we write:
()
actual
q
max
′′′
= Σ
fr
E
d
φ
max
= Σ
fr
E
d
(
φ
av
ȗ) = Σ
fr
E
d
)
V
(
Rf
E
Q
Σ
ζ
= Σ
fr
E
d
)
V)/(
(
2
2
Rrodfr
ERaN
Q
Σ
ζ
or alternatively;
()
actual
q
max
′′′
=
2
H
d
rod R
QE
aN E
ζ
π
Heat flux distribution. We obtained the volumetric heat generation rate in a
cylindrical core in Equation VIe.3.4. To obtain similar distribution, but for core
heat flux, we write the relation between power, linear heat generation rate, heat
flux and volumetric heat generation rate for a fuel rod as:
HHPH
FF
AqqqQ
′′′
=
′′
=
′
=
VIe.3.5
where H is the rod length, P
F
is the fuel pellet perimeter, and A
F
is the fuel pellet
cross sectional area. Thus, Equation VIe.3.4 can also be written as:
864 VIe. Applications: Nuclear Heat Generation
q
′′
(r, z) =
max
q
′′
J
o
¸
¹
·
¨
©
§
R
r405.2
cos
¸
¹
·
¨
©
§
H
z
π
VIe.3.6
where
q
′′
is the local and
max
q
′′
is the maximum fuel rod heat flux.
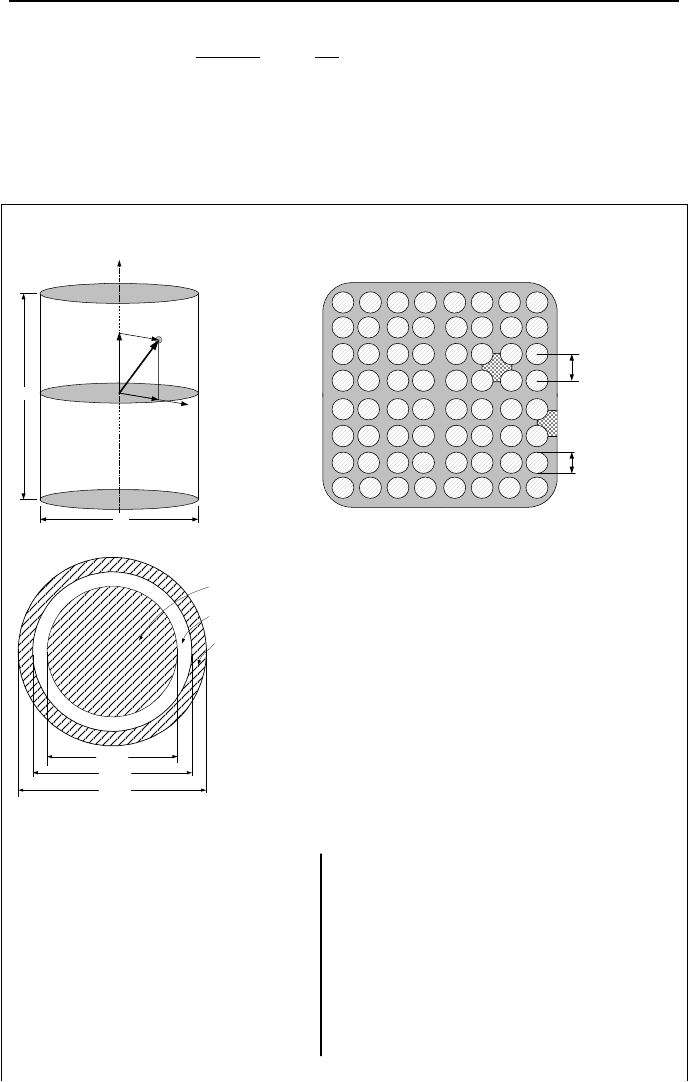
Example VIe.3.2. Data for a BWR core, bundle, and rod are given as follows:
Z
P
P
z
r
H
D
s
d
c2
d
F
d
F
d
C2
d
C1
Fuel
Clad
Gap
D: Core diameter (ft): 16 H: Core height (ft): 12
n: Rods per bundle: 64 s: Pitch (in): 0.74
d
C1
: Clad in-dia. (in): 0.50 d
C2
: Clad out-dia. (in): 0.56
Q
: Core power (MWth): 3,300
ρ
: UO
2
density (lbm/ft
3
): 644
N: Number of fuel bundles: 585
d
F
: Pellet diameter (in): 0.48
δ: Clad thickness (in): 0.03
Ω:
av
qq
′′′′′′
/
max
: 2.5

3. Determination of Neutron Flux in an Infinite Cylindrical Core 865
Find,
a) total weight of UO
2
in kg,
b) core average power density in kW/lit,
c) specific power in kW/kg,
d) average linear heat generation rate in kW/ft,
e) average heat flux in kW/ft
2
,
f) the maximum volumetric heat generation rate in kW/ft
3
, and g) the volumetric
heat generation rate at r = R/2 and z = H/3.
Solution:
a) We first find total volume and mass of UO
2
:
58.564)58588()4/12()12/48.0(4/HV
22
UO
2
=×××××==
ππ
F
d ft
3
58.56485.643V
2
UO
×==
ρ
M = 363,505 lbm = 164,667.7 kg ≅ 165 tons
b) We now calculate core volume:
Core
V =
π
D
2
H/4 =
π
× (16/3.2808)
2
× (12/3.2808)/4] = 68.32E3 lit
By definition:
CoreCore
QDP V/..
= = 3,300 × 1000/68.32E3 = 48.3 kW/lit
c) By definition: ==
2
UO
/.. MQPS
Core
3,300 × 1000/164,667.7 = 20 kW/kg
d) By definition: ]12)88585/[(1000300,3)H/( ××××=×=
′
RodCore
NQq
=
7.3 kW/ft
e)
2
/( H) 3,300 1000 /[(585 8 8) (0.56 /12) 12]
Core Rod C
qQ N d
ππ
=×=××××××
′′
= 50 kW/ft
2
f)
()
200)58564((0.48/12)12
1801000300,316.1
H
16.1
22
max
××××
×××
==
′′′
RRod
d
Bare
ENa
PE
q
= 4792.67 kW/ft
3
ππ
ζ
16.1
5.2
67.4792
16.1
H
16.1
2
max
×=
¸
¹
·
¨
©
§
=
′′′
RRod
d
ENa
PE
q
= 3287.83 kW/ft
3
g) Since )
H
cos()
405.2
(),(
max
z
R
r
Jqzrq
o
π
′′′
=
′′′
then ),( zrq
′′′
= 3287.83 × J
o
[(2.405 × R/2)/R] × cos[(
π
× H/3)/H] = 3287.83 ×
0.669 × 0.5 = 1099.78 kW/ft
3

866 VIe. Applications: Nuclear Heat Generation
Average heat generation rate. We find the core average heat generation rate
from:
³
=
′′′
=
′′′
V
V),(
V
dzrq
q
¸
¹
·
¨
©
§
HR
2
1
π
¸
¸
¹
·
¨
¨
©
§
H
16.1
2
aNE
QE
rodR
d
»
»
¼
º
«
«
¬
ª
µ
¶
´
¸
¹
·
¨
©
§
»
»
¼
º
«
«
¬
ª
µ
¶
´
¸
¹
·
¨
©
§
−
2/H
2/H0
cos)2(
405.2
dz
H
z
rdr
R
r
J
R
o
π
π
If we carryout the integrals in the radial and the axial directions, we find
=
′′′
q
max
q
′′′
/(2.316 × 1.57). Writing in terms of heat flux by using Equa-
tion VIe.3.5 and representing F
N
= 2.316 × 1.57 we obtain:
max
q
′′
= q
′′
× F
N
VIe.3.7
where in Equation VIe.3.7, F
N
is known as the nuclear peaking factor. The first
multiplier,
axial
N
F = 2.316, is the axial peaking sub-factor and the second multi-
plier,
radial
N
F = 1.57, is the radial peaking sub-factor.
3.1. Axial Temperature Distribution
We use the volumetric heat generation rate, as given by Equation VIe.3.3 to de-
termine the axial temperature distribution in the reactor core. To limit the analysis
to only one variable, we choose the central channel for which r = 0 hence J
o
= 1.
We also limit the analysis to PWRs
*
where coolant entering and leaving the core
remains subcooled. This assumption allows us to write dh = c
p
dT. Using sub-
script f for the bulk coolant, F for the fuel, and applying Equation IIa.6.6 to an
elemental control volume taken at axial location z (Figure VIe.3.2(c)), yields:
)( dhhmQdhm +=+
Simplifying, we find QddTcm
fp
= . For the fuel rod of Figure VIe.3.2,
HHPH
2 FC
AqqqQ
′′′
=
′′
=
′
=
where P
C2
,=
π
d
C2
,and A
F
=
π
2
F
d /4. Substituting
for total rate of heat generation we get:
dzAzqqddTcm
Ffp
)(
′′′
==
We now substitute from Equation VIe.3.3 and integrate from the core inlet to any
elevation:
*
Note we are assuming that boiling does not occur even in the hot channel.
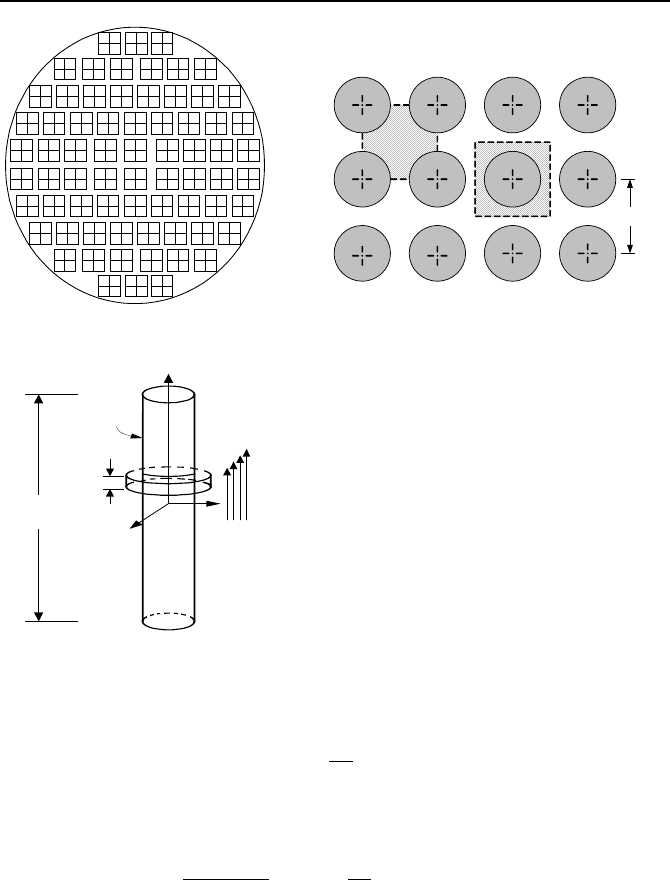
3. Determination of Neutron Flux in an Infinite Cylindrical Core 867
s
(a) (b)
dz
T
f
h
T
c 2
H
(c)
Figure VIe.3.2. (a) Core, (b) Fuel rods, and (c) Central rod and channel
³
µ
¶
´
¸
¹
·
¨
©
§
′′′
=
−
−
z
F
z
fp
dz
z
qAdTcm
2/H
max
2/H
H
cos
π
Carrying out the integral and simplifying, we obtain the coolant temperature as:
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
+
′′′
+=
H
sin1
H
)(
max
,
z
cm
Aq
TzT
p
F
inff
π
π
VIe.3.8
Having the coolant temperature, we can find the clad outside temperature from a
steady state heat balance:
()
()
fCC
TTdzhQd −=
22
P
Substituting for the rate of heat transfer and for fluid temperature and solving for
clad temperature, we get:

868 VIe. Applications: Nuclear Heat Generation
¸
¹
·
¨
©
§
′′′
+
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
+
′′′
+=
H
cos
PH
sin1
V
)(
2
maxmax
,2
z
h
Aq
z
cm
q
TzT
C
F
p
F
infC
ππ
π
VIe.3.9
In this equation, we assumed that the heat transfer coefficient, h, remains constant
from inlet to any elevation. Having the clad outside temperature, we can find clad
inside temperature, T
C1
, fuel surface temperature, T
F2
, and fuel centerline tempera-
ture by using the corresponding thermal resistances. Following the procedure that
led to derivation of Equation IVa.6.15, we can find each temperature in terms of
T
f, in
, m
, and
max
q
′′′
as:
¸
¹
·
¨
©
§
′′′
++
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
+
′′′
+=
H
cos)(V
H
sin1
V
)(
max
max
,1
z
qRR
z
cm
q
TzT
CfF
p
F
infc
ππ
π
VIe.3.10
¸
¹
·
¨
©
§
′′′
+++
»
¼
º
«
¬
ª
¸
¹
·
¨
©
§
+
′′′
+=
H
cos)(V
H
sin1
V
)(
max
max
,2
z
qRRR
z
cm
q
TzT
GCfF
p
F
infF
ππ
π
VIe.3.11
max
,
max
1
V
() 1 sin
H
V( ) cos
H
F
fin
p
FF
CG
f
F
q
z
TzT
mc
z
RRRRq
π
π
π
ªº
§·
«»
¨¸
©¹
¬¼
§·
¨¸
©¹
′′′
=+ + +
+++
′′′
VIe.3.12
where the thermal resistance of fuel (R
F
), gap (R
G
), clad (R
C
), and flow (R
f
) are the
terms in the denominator of Equation IVa.6.15. Temperature distributions of the
coolant, clad, and fuel are shown in Figure VIe.3.3.
As we expect, the coolant temperature peaks at the channel exit due to the ac-
cumulation of heat. However, the fuel rod temperature is a function of both cool-
ant temperature and the volumetric heat generation rate. While the coolant tem-
perature keeps increasing along the channel, the volumetric heat generation rate is
at its maximum at the center and then keeps decreasing, due to the cos(
π
z/H) mul-
tiplier. Therefore, the axial fuel rod temperature increases until a maximum tem-
perature is reached, the location of which is expectedly above the core center-
plane and below the channel exit.
Now that we evaluated the axial temperature distribution of the fuel rod at a
given radius, let’s evaluate the radial temperature distribution of the fuel rod at a
given axial location. By expressing fuel rod temperature at various radial loca-
tions (Equations VIe.3.9 through VIe.3.12) with temperature at each location be-
ing a function of z, we have used a two-dimensional approach for the fuel rod
temperature, albeit for selected nodes. Note that by using a single control volume
for the coolant, its temperature in the radial direction is lumped. Since at any axial
location, fuel rod temperature is a function of both T
f
and
max
q
′′′
, it is then expected
that temperature further inside the fuel rod is influenced more by
max
q
′′′
and less by
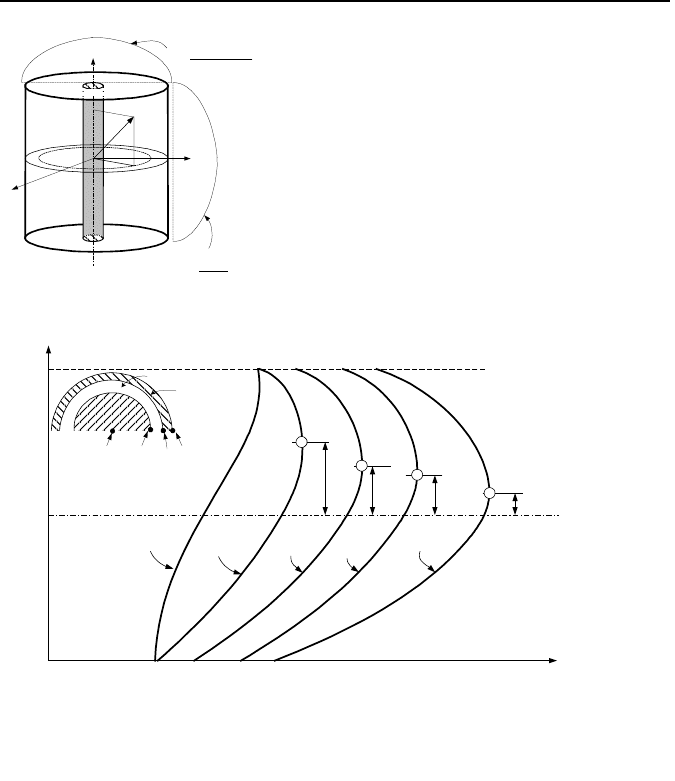
3. Determination of Neutron Flux in an Infinite Cylindrical Core 869
x
y
z
J
o
2.405r
R
()
)
H
cos(
z
π
Fuel
Gap
Clad
H/2
-H/2
z
C2
z
F2
z
F1
z
C1
Coolant
Clad
Inside
Clad
Outside
Fuel
Surface
Fuel
Center
Temperature
T
F1
T
C2
T
F2
T
C1
z
Figure VIe.3.3. Two dimensional tem
p
erature distribution of a fuel rod in the hot channel
of a PWR
T
f
. This is shown by the elevations from the point of maximum temperature to
the core center-plane for various radial location as clad outside (z
C2
), clad inside
(z
C1
), fuel surface (z
F2
), and fuel centerline (z
F1
).
To find the location of the maximum temperatures, we take the derivative of
the related equation for temperature and set it equal to zero. By substituting the
location at which temperature is maximum, we can obtain the value of T
max
in
terms of all the known variables for any radial location of the fuel rod. For exam-
ple, for clad outside temperature, we take the derivative of Equation VIe.3.9 and
set it equal to zero:
()
()
fpc
Rcmz
ππ
1
max,2
tan//H
−
=

870 VIe. Applications: Nuclear Heat Generation
Example VIe.3.3. A PWR core contains 217 fuel assemblies, each on the average
containing 176 fuel rods, operating at 2700 MWth.. Use the data given below and
find the location and the value of the peak clad outside temperature. Data: H = 12
ft, m
= 138.5E6 lbm/h, d
F2
= 0.377 in, d
C2
= 0.44 in, h = 4000 Btu/h·ft
2
F, c
p
=
1.392 Btu/lbm·F, T
f, in
= 550 F, and Ω = 2.56.
Solution: We first find the number and volume of the rods:
N
rod
= 217 × 176 = 38,192
V
F
=
π
(d
F2
)
2
/4 × H =
π
(0.377/12)
2
× 12/4 = 9.3E–3 ft
3
We now find thermal resistance of the coolant film:
R
f
= (
π
d
C2
H)h = 1/[
π
× (0.44/12) × 12 × 4000] =
1.81E–4 h·ft
2
·F/Btu (3.186E–5 m
2
·K/W)
Z
C2, max
= (12/
π
)/tan
–1
[
π
× (138.5E6/38,192) × 1.392 × 1.81E–4] = (12/
π
)/1.235 =
3.1 ft (1 m)
The maximum volumetric heat generation rate is found from:
max
2
H
d
Rrod
EQ
q
EN a
ζ
π
§·
=′′′
¨¸
©¹
=
2
180 2700 2.56
200 38,192 [(0.377 / 2) /12] 12
π
××
=
×× × ×
17.51 W/ft
3
= 5.97E7 Btu/h·ft
3
The peak clad outside temperature is found from Equation VIe.3.9 by substituting
for z = z
c2,max
= 3.1:
T
C2
,
max
= 550 +
5.97E7 9.3E 3 3.1
1sin
(138.5 6 / 38,192) 1.392 12E
π
π
×− ×
§·
++
¨¸
©¹
××
5.97E7 9.3E 3 3.1
cos
1/181 4 12
E
π
×− ×
−
= 680 F
Example VIe.3.4. Shown in the figure is the surface heat flux of a rod in an ex-
perimental reactor. Use the given data and find a) coolant temperature, b) clad
surface temperature, and c) fuel centerline temperature at z = H/2. Data: H = 6 ft,
d
F2
= d
C1
= 0.4 in, d
C2
= 0.5 in, T
f,in
= 155 F, m
= 375 lb/hr per rod, h = 2000
Btu/h·ft
2
·F, k
F
= 1 and k
C
= 3 Btu/h·ft·F,
1
q
′′
= 120,000 Btu/hr ft
2
,
1
q
′′
= 250,000
Btu/hr·ft
2
.
z
q
′′
1
q
′′
2
q
′′
)2/H(
)2/H(
)(
121
+
′′
−
′′
+
′′
=
′′
z
qqqq
)2/H(
)2/H(
)(
212
−
′′
−
′′
−
′′
=
′′
z
qqqq
H
z = 0
Fuel Clad
T
C2
T
F1
T
C1

3. Determination of Neutron Flux in an Infinite Cylindrical Core 871
Solution:
a) We write an energy balance for an elemental control volume and integrate:
[]
³³
dzdzqdzdzqTzTcm
z
inffp
)()()()()(
0
0
2/H
,
ππ
′′
+
′′
=−
−
We then substitute for heat flux and carrying out the integral:
,
0
22
121 121
H/2 0
()
(/2)(H/2) (/2)(H/2)
() ()
H/2 H/2
p
ffin
z
mc T z T
z
zzz
dqz q q q q q
π
−
ªº
«»
¬¼
ª º
§·§·
« »
¨¸¨¸
« »
¨¸¨¸
©¹©¹
« »
¬ ¼
−=
+−
+− +−−
′′ ′′ ′′ ′′ ′′ ′′
Solving for T
f
(z) and substituting values, we find:
()
=
′′
+
′′
+=
21,
2
H
)( qq
cm
d
TzT
p
inff
π
()
5E5.25E2.1
13752
6)12/5.0(
155 +
××
××
+
π
= 542.5 F
b) From a transverse heat balance we also find:
[]
hzqzTzT
fC
/)()()(
2
′′
+=
Substituting values to get:
5.602
2000
5E2.1
5.542/
H/2
)2/H(
)()(
1212
=+=
»
¼
º
«
¬
ª
−
′′
−
′′
−
′′
+= h
z
qqqzTT
fC
F
c) We find, T
F1
from another energy balance:
[]
RzTzTzdzqzQ
CFC
Σ−=
′′
= /)()())(()(
212
π
()
1
12
221
2
)/ln(
4
1
q
k
dd
k
dTT
C
CC
F
CCF
′′
»
¼
º
«
¬
ª
++=
= =×
»
¼
º
«
¬
ª
×
+
×
+= 5E2.1
32
)4.0/5.0ln(
14
1
12
5.0
474
1F
T 1910 F
3.2. Determination of Incipient Boiling
In BWRs we often need to find the surface temperature and its location corre-
sponding to the inception of subcooled boiling. As was discussed in Chapter Vb,
such local temperature is not a single fixed temperature. Still, we can estimate a
value for it from the following relation:
