Massoud M. Engineering Thermofluids: Thermodynamics, Fluid Mechanics, and Heat Transfer
Подождите немного. Документ загружается.

692 VIa Applications: Heat Exchangers
T
T
h,in
T
h,out
T
c,out
T
c,in
dT
h
dT
c
∆T
∆T
0
∆T
L
x
dx
Cold Stream CV
Hot Stream CV
Tube CV
0
L
T
T
h,in
T
h,out
T
c,in
T
c,out
dT
h
dT
c
∆T
∆T
0
∆T
L
x
dx
Cold Stream CV
Hot Stream CV
Tube CV
0
L
(a) (b)
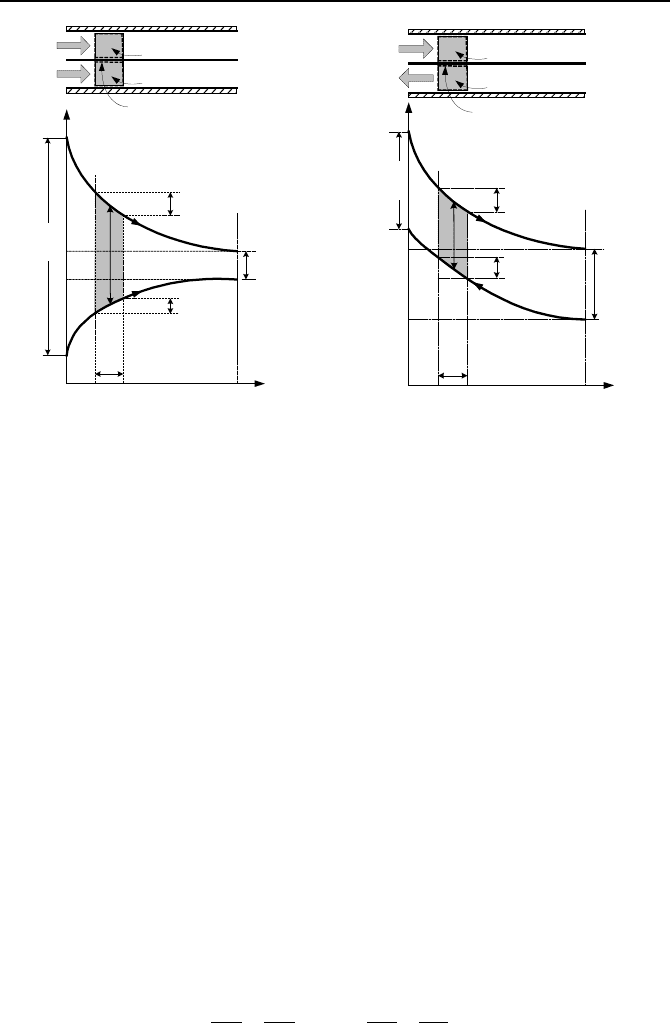
Figure VIa.2.2. Hot and cold temperature profiles for (a) parallel and (b) counterflow heat
exchangers
Consider three elemental control volumes, one for the hot side, one for the tube
surface, and one for the cold side of a heat exchanger, Figure VIa.2.2(a) and
VIa.2.2(b). These figures show the temperature profiles as a function of the heat
exchanger length. Similar to Equations VIa.2.4a and VIa.2.4b, we can write axial
energy equations for the hot side and cold side of the elemental control volumes:
hh
dTCQd −=
VIa.2.6a
cc
dTCQd =
VIa.2.6b
We now write the transverse energy equation assuming negligible axial heat con-
duction in the tube. Such thermal resistances as flow, tube wall, and fouling are
taken into account by the use of an overall heat transfer coefficient:
TxdAxUQd ∆= )]()([
VIa.2.7
Note that the term ∆T in Equation VIa.2.7 represents the difference in the average
temperatures of the hot and cold side elemental control volumes (i.e. ∆T = T
h
–
T
c
). To relate Equations VIa.2.6a and VIa.2.6b to Equation VIa.2.7, we differenti-
ate ∆T and substitute for terms:
d(∆T) = dT
h
– dT
c
=
ch
C
Qd
C
Qd
−−
=
)
11
(
ch
CC
Qd +−
VIa.2.8

2. Analytical Solution 693
If we integrate Equation VIa.2.8 from x = 0 to x = L, we get:
)
11
(
0
ch
L
CC
QTT +=∆−∆
VIa.2.9
We may also substitute in Equation VIa.2.8 for
Qd
from Equation VIa.2.7 and
divide by ∆T to obtain:
)
11
)](()([
)(
ch
CC
xdAxU
T
Td
+−=
∆
∆
Integrating the above equation from x = 0 to x = L, yields:
³
)()(]
11
[
)(
0
0
xdAxU
CCT
Td
L
ch
L
+−=
µ
¶
´
∆
∆
VIa.2.10
We now define an overall heat transfer coefficient, which is averaged over the
heat exchanger length:
³
A
xdAxU
U
L
0
)()(
=
where A is the heat exchanger surface area. By defining the average U, Equation
VIa.2.10 becomes:
)
11
(ln
0
chL
CC
UA
T
T
+=
∆
∆
VIa.2.11
Substituting for 1/C
h
+ 1/C
c
from Equation VIa.2.9 we find:
0
0
ln( / )
L
LMTD
L
TT
QUA UAT
TT
∆−∆
==∆
∆∆
VIa.2.12
Note that in applying Equation VIa.2.12 to parallel and counterflow heat exchang-
ers, we must recall that (see Figure VIa.2.2):
Parallel Flow: ∆T
0
= T
h,in
– T
c,in
and ∆T
L
= T
h,out
– T
c,out
Counterflow: ∆T
0
= T
h,in
– T
c,out
and ∆T
L
= T
h,out
– T
c,in
For the same inlet and outlet temperatures, (∆T
LMTD
)
Counterflow
> (∆T
LMTD
)
Parallel
.
This implies that for the same U and A, a counterflow heat exchanger has a higher
rate of heat removal than a parallel flow heat exchanger. Comparing Equation
VIa.2.5 with Equation VIa.2.12, we note that the temperature difference unfortu-
nately contains a logarithmic term. This complicates analysis when unknown
temperatures must be found from Equation VIa.2.12.
694 VIa Applications: Heat Exchangers
Example VIa.2.1. Use the given data to find a) ∆T
LMTD
if the heat exchanger uses
a parallel flow arrangement and b) ∆T
LMTD
if the heat exchanger uses a counter-
flow arrangement. Data: T
h,i
= 195 F, T
h,o
= 160 F, T
c,i
= 65 F, and T
c,o
= 105 F.
T
T
h,in
= 195 F
T
h,out
=160 F
T
c,out
=105 F
T
c,in
= 65 F
∆T
0
= 130 F
∆T
L
= 55 F
x
T
T
h,in
= 195 F
T
h,out
=160 F
T
c,in
= 65 F
T
c,out
= 105 F
∆T
0
= 90 F
∆T
L
= 95 F
x
Solution: a) For parallel flow, ∆T
0
= T
h,i
– T
c,i
= 195 – 65 = 130 F, and ∆T
L
= T
h,o
– T
c,o
= 160 – 105 = 55 F
[∆T
LMTD
]
Parallel
= [130 – 55]/ln(130/55) = 87.2 F
b) For counterflow, ∆T
0
= T
h,i
– T
c,o
= 195 – 105 = 90 F, and
∆T
L
= T
h,o
– T
c,i
= 160 – 65 = 95 F
[∆T
LMTD
]
Counterflow
= [90 – 95]/ln(90/95) = 92.5 F
Comment: Two observations can be made from this example. First, as discussed
earlier and shown above (∆T
LMTD
)
Counterflow
> (∆T
LMTD
)
Parallel
. In this example, for
the same U and A, the counterflow HX is more efficient than the parallel flow HX
by about 6%. Second, an average temperature difference per Equation VIa.2.5 is
∆T = [(195 + 160) – (105 + 65)]/2 = 92.5 F, which happens to agree with
(∆T
LMTD
)
Counterflow.
Equations and Unknowns. For a concentric heat exchanger, we derived three
equations, namely two axial energy equations (Equations VIa.2.4a and VIa.2.4b)
and a transverse energy equation (Equation VIa.2.12). The number of unknowns,
being nine, exceeds the number of equations by a wide margin. The unknowns are
AUTTTTmmQ
outcouthincinhch
and,,,,,,,,
,,,,
. Note that c
p,h
and c
p,c
are not un-
knowns as they are functions of the related temperatures. We have an additional
equation for U given by Equation VIa.1.1, which introduces h
i
, h
o
, f
i
, f
o
, d
i
, d
o
, and
L. However, the heat transfer coefficients are functions of Re, Pr, fluid tempera-
ture, d
i
, and d
o
. Also the heat exchanger surface area is related to tube diameter
and tube length as A =
π
dL. An additional unknown is the shell diameter, which
can be calculated from an appropriate equation. We increased the number of
equations to eight. These are Equations VIa.2.4a, VIa.2.4b, VIa.2.12, VIa.1.1,
V.3.4 (for h
i
and a similar equation for h
o
), the relation for A = f(d, L), and the re-
lation for D
shell
. However, we increased the number of unknowns to seventeen!
To have a consistent set, we must then specify nine of the unknowns. This argu-

2. Analytical Solution 695
ment indicates that, from the thermal analysis point of view, heat exchangers have
a large degree of freedom. On the other hand, constraints for design optimization
include:
– structural considerations (tube outside diameter to stand internal pressure)
– hydraulic considerations (tube inside diameter for pumping power and pressure
drop in tube)
– performance (fouling characteristics of the working fluids)
– tube material (conductivity, erosion, and corrosion characteristics)
– size and weight limitations
– cost
Returning to the three equations and nine unknowns discussion, let’s consider a
case where two inlet temperatures (T
h,in
and T
c,in
), two flow rates (
h
m
, and
h
m
),
the heat transfer coefficient U, and the surface area A are specified. We solve for
the two exit temperatures (T
h,out
and T
c,out
) and the rate of heat transfer Q
. We
substitute for the two exit temperatures from Equations VIa.2.4a and VIa.2.4b into
Equation VIa.2.12 to solve for
Q
:
)/1()/(
)1)((
,,
ch
incinh
CC
TT
Q
−
−−
=
β
β
VIa.2.13
where
]/1/1[
,, cpchph
cmcmUA
e
−
=
β
. This equation is applicable to counterflow heat
exchangers. See Section 2.2 for generalization of this method.
Example VIa.2.2
. Water flows in both sides of a counterflow heat exchanger.
Find the rate of heat transfer Q
, and exit temperatures (T
h,out
and T
c,out
) for the fol-
lowing data: T
h,i
= 130 F, T
c,i
= 95 F, 6E5.1=
h
m
lbm/h, 6E41.2=
c
m
lbm/h,
U = 259 Btu/ft
2
·h·F, A = 5,790 ft
2
, and c
p
= 1 Btu/lbm·F.
Solution: To use Equation VIa.2.13, we find
β
= exp[259 × 5,790(1/1.5E6 – 1/2.41E6)] = 1.4586
)(
,, outhinhh
TTCQ −=
= (130 –95) × (1.4586 – 1)/[1.4586/1.5E6 – 1/2.41E6] =
28.8E6 Btu/h
T
h,out
= )/(
, hinh
CQT
− = 130 – (28.8E6/1.5E6) = 111 F
T
c,out
= )/(
, cinc
CQT
+ = 95 + (28.8E6/2.41E6) = 107 F.
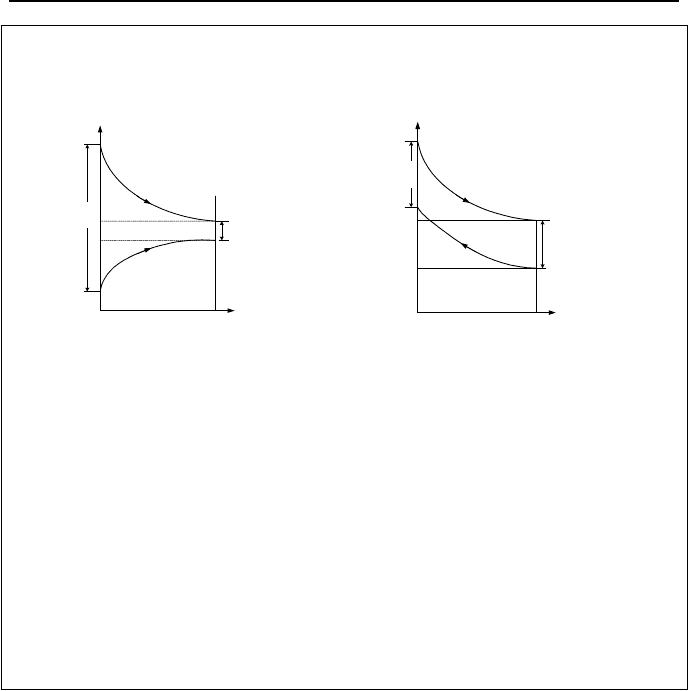
Special Modes of Operation. Shown in Figure VIa.2.3 are three different
modes of operations. Figure VIa.2.3(a) shows one stream is boiling while the
other stream is cooling down. In this case (i.e., in the case of a steam generator)
0→∆T and ∞→
c
C . Figure VIa.2.3(b) shows one stream is condensing

696 VIa Applications: Heat Exchangers
T
T
h,in
T
h,out
T
c
dT
h
∆T
∆T
0
x
dx
Cold-side Boiling
∆T
L
T
c
T
c
T
T
h
T
c,out
T
c,in
dT
c
∆T
∆T
0
x
dx
Hot-side Condensing
∆T
L
T
h
0 L
(a) (b)
T
T
c,out
T
c,in
dT
c
∆T
∆T
0
∆T
L
L
dx
T
h,in
T
h,out
dT
h
cpchph
cmcm
,,
=
x
∆T
0
= ∆T
L
0
(c)
Figure VIa.2.3. (a) Steam generator, (b) Condenser, and (c) Special case of ∆T
h
= ∆T
c
while the other stream is heating up. In this case (i.e. in the case of a condenser),
we have
0→∆T and ∞→
h
C . Note that in these cases we should use Equa-
tions VIa.2.3a and VIa.2.3b. Finally, Figure VIa.2.3(c) shows a special case in
which C
h
= C
c
. This requires that ∆T
h
= ∆T
c
.
Multi-pass Heat Exchangers. The LMTD method outlined above and the re-
sult culminated in Equation VIa.2.12 apply to concentric heat exchangers (Fig-
ure IVa.6.3). The same results can be applied to the shell and tube heat exchang-
ers with multi-pass tubes and shell, by applying a correction factor F
multi-pass
so
that:
LMTDpassMulti
TUAFQ ∆=
−
VIa.2.12a
The F
Multi-pass
factor is given in Figure VIa.2.4 for two cases. The left side figure is
for any multiples of two tube pass (four, six, etc.) and one shell pass. The right

2. Analytical Solution 697
side figure is for any multiple of four tube and two shell passes. In these figures,
the tube-side inlet and outlet temperatures are shown by t
i
and t
o
whereas the shell-
side inlet and outlet temperatures are shown by Ti and T
o
, respectively. The cor-
rection factor obtained from Figure VIa.2.3 should be used in conjunction with the
∆
T
LMTD
calculated for a counterflow configuration. The correction factor for one
shell path, as shown in the left side plot of Figure VIa.2.4 is obtained from:
2
22
1
1
ln[(1 ) /(1 )]
ln{[2 ( 1 1)]/[2 ( 1 1)]}
Multi pass
R
F
R
PPR
PR R PR R
−
+
=×
−
−−
−+−+ −+++
VIa.2.14
Parameters P and R in Figure VIa.2.4 and in Equation VIa.2.11 are known as ca-
pacity ratio and effectiveness, respectively and are given as:
Capacity Ratio:
ii
i
h
c
tT
tt
C
C
P
−
−
==
0
Effectiveness:
io
oi
ioh
oic
tt
TT
ttC
TTC
R
−
−
=
−
−
=
)(
)(
Figure VIa.2.4. Correction factor for multiple tube and shell passes
The LMTD correction factor (F) for multi-pass shell and tube heat exchangers
can be calculated by using the software on the accompanying CD-ROM.
Example VIa.2.3. Seawater is used to cool the lubricating oil of a ship’s diesel
engine. The shell and tube heat exchanger has one shell and two tube passes.
Tube surface area is 100 ft
2
and the overall heat transfer coefficient is given as U =
250 Btu/ft
2
·h·F. Oil enters at 160 F and leaves at 125 F. Water enters the tube at
75 F and leaves at 100 F. Find the total rate of heat transfer.

698 VIa Applications: Heat Exchangers
Solution: We find the capacity ratio and the effectiveness as follows,
P = (100 – 75)/(160 – 75) = 0.294. R = (160 – 125)/(100 –75) = 1.4
Using the left plot of Figure VIa.2.3, we find F
Multi-pass
≈ 0.95
∆T
LMTD
= [(160 – 100) – (125 – 75)]/ln[(160 – 100)/(125 – 75)] = 54.85 F
Q
= F
Multi-pass
UA
∆
T
LMTD
= 0.95 × 250 × 100 × 54.85 = 1.3E6 Btu/h ≈ 0.4 MW.
Cross Flow Heat Exchangers. Equation VIa.2.12 is also applicable to cross
flow heat exchangers:
LMTDCrossFlow
TUAFQ ∆=
VIa.2.12b
where F
Cross Flow
is given in Figure VIa.2.5 for two cases. The left figure is for a
case where both streams are unmixed and the right figure is for one stream mixed
and other stream unmixed.
Figure VIa.2.5. Cross flow heat exchangers
2.2. NTU Method of Analysis
In cases where exit temperatures are unknown, we have to solve an equation in-
volving the logarithmic term for ∆T
LMTD
. An alternative method of analyzing heat
exchangers is the
ε
– NTU method where NTU = UA/C stands for number of trans-
fer units, and effectiveness (now represented by
ε
) is given as:
)(
,,min incinh
actual
ideal
actual
TTC
Q
Q
Q
−
==
ε
2. Analytical Solution 699
where C
min
is the minimum of C
h
and C
c
. The ideal or maximum rate of heat
transfer is associated with maximum ∆T, which is ∆T
max
= T
h,in
– T
c,in
. If we find
ε
, then we can calculate
actual
Q
from:
maxmin
TCQ
actual
∆=
ε
Therefore, in the
ε
-NTU method, rather than calculating ∆T
LMTD
we calculate
ε
,
which depends on the type of heat exchanger and flow configuration. Since
)()(
,,,, incoutccouthinhhactual
TTCTTCQ −=−=
, then
)(
)(
,.min
,,
incinh
outhinhh
TTC
TTC
−
−
=
ε
VIa.2.15a
and
)(
)(
,.min
,,
incinh
incoutcc
TTC
TTC
−
−
=
ε
VIa.2.15b
We use Equations VIa.2.15a, VIa.2.15b, and VIa.2.11 to derive relations for
ε
for
various types of heat exchangers. For example, for a parallel flow heat exchanger,
we can write Equation VIa.2.11 as:
)]/1/1(exp[
,,
,,
0
ch
incinh
outcouth
L
CCUA
TT
TT
T
T
+−=
−
−
=
∆
∆
We now solve Equation VIa.2.15a for T
h,out
and substitute in the above equation to
get:
)]/1/1(exp[)1(1
,,
,,
ch
h
c
incinh
incoutc
CCUA
C
C
TT
TT
+−=+
−
−
−
Substituting for the temperature ratio term in the above equation from Equa-
tion VIa.2.15b yields:
hc
ch
CCCC
CCUA
//
)]/1/1(exp[1
minmin
+
+−−
=
ε
If it happens that C
c
< C
h
, then C
min
= C
c
and the denominator becomes 1 + C
c
/C
h
.
Conversely, for the case of C
h
< C
c
, the denominator becomes 1 + C
h
/C
c
. We can
write the result in compact form of 1 + C
r
where C
r
= C
min
/C
max
. Similarly, in the
numerator, we factor out C
min
and substitute for UA/C
min
= NTU:
700 VIa Applications: Heat Exchangers
maxmin
maxmin
/1
)]/1(exp[1
CC
CCNTU
+
+−−
=
ε
VIa.2.16
Equation VIa.2.16 gives the effectiveness as a function of NTU,
ε
= f(NTU, C
r
).
We may also solve Equation VIa.2.16 for NTU as a function of
ε
, NTU = f(
ε
,
C
r
).
The same method used to derive Equation VIa.2.16 for the parallel flow heat ex-
changers can be applied to other types of heat exchangers and obtain similar rela-
tions for effectiveness (Kays). The results for
ε
as a function of NTU and C
r
=
C
min
/C
max
are summarized in Table VIa.2.1. This is followed by the results ob-
tained from Kays for NTU = f(
ε
), as shown in Table VIa.2.2.
Example VIa.2.4. Water flows in both sides of a counterflow heat exchanger.
Find the rate of heat transfer Q
, and exit temperatures, T
h,out
, and T
c,out
for the fol-
lowing data: T
h,in
= 55 C, T
c,in
= 30 C, =
h
m
200 kg/s, =
c
m
300 kg/s,
U = 1.5 kW/m
2
·C, and A = 540 m
2
, c
p
= 4.18 kJ/kg·K.
Solution: In this example, C
min
= C
h
= 200 × 4.18 = 836 kW/C
min
1.5 540
0.97
836
UA
NTU
C
×
== =
200 4.18
0.667
300 4.18
r
C
×
==
×
1exp[ (1 )]
1exp[ (1)]
r
rr
NTU C
CNTUC
ε
−− −
=
−−−
=
1exp[0.97(10.667)]
0.534
1 0.667 exp[ 0.97 (1 0.667)]
−−×−
=
−×−×−
Q
max
= C
min
(T
h,in
– T
c,in
) = 200 × 4.18 × (55 – 30) = 20,900 kW
Q
actual
=
ε
Q
max
= 0.534 × 20,900 = 11,161 kW
Having Q
actual,
we can find exit temperatures as:
,
11,161
55 42
200 4.18
hout
T =− =
×
C
,
11,161
30 39
300 41.8
c out
T =+ =
×
C.

2. Analytical Solution 701
Table VIa.2.1. Heat exchanger effectiveness for various flow arrangements
Flow Arrangement Effectiveness
Parallel Flow:
1exp[ (1 )]
1
r
r
NTU C
C
ε
−− +
=
+
Counterflow:
1exp[ (1 )]
1exp[ (1)]
r
rr
NTU C
CNTUC
ε
−− −
=
−−−
Shell & tube
(1 shell pass, 2, 4, … n tubes passes):
1
2/12
2/12
2/12
1
])1(exp[1
])1(exp[1
)1(12
−
¿
¾
½
¯
®
+−−
+−+
+++=
r
r
rr
CNTU
CNTU
CC
ε
Shell & tube
(n shell pass, 2n, 4n,… tube passes):
1
1
1
1
1
1
1
1
1
1
−
»
»
¼
º
«
«
¬
ª
−
¸
¸
¹
·
¨
¨
©
§
−
−
»
»
¼
º
«
«
¬
ª
−
¸
¸
¹
·
¨
¨
©
§
−
−
=
r
n
r
n
r
C
CC
ε
ε
ε
ε
ε
Cross flow
(single path, both streams unmixed):
0.22 0.78
1 exp[(1 )( ) {exp[ ( ) ] 1}]
rr
C NTU C NTU
ε
=− − −
Cross flow (C
max
mixed, C
min
unmixed): (1 )(1 exp{ [1 exp( )]})
rr
CCNTU
ε
=−−−−
Cross flow (C
max
unmixed, C
min
mixed):
1
1exp( {1exp[ ( )]})
rr
CCNTU
ε
−
=− − − −
Heat exchangers with C
r
= 0:
1exp( )NTU
ε
=− −
Table VIa.2.2. Heat exchanger NTU for various flow arrangements
Flow Arrangement Number of Transfer Units
Parallel Flow:
ln[1 (1 )]
1
r
r
C
NTU
C
ε
−+
=−
+
Counterflow:
¸
¸
¹
·
¨
¨
©
§
−
−
−
−=
1
1
ln
1
1
rr
CC
NTU
ε
ε
Shell & tube (1 shell pass, 2, 4, … n tubes pass):
¸
¸
¹
·
¨
¨
©
§
+Ε
−Ε
+−=
−
1
1
ln)1(
2/12
r
CNTU
,
1
21/2
2/ (1 )
(1 )
r
r
C
C
ε
−+
Ε=
+
Cross flow (C
max
mixed, C
min
unmixed): )]1ln()1(1ln[
rr
CCNTU
ε
−+−=
Cross flow (C
max
unmixed, C
min
mixed): ]1)1ln(ln[)1( +−−=
ε
rr
CCNTU
Heat exchangers with C
r
= 0: )1ln(
ε
−−=NTU
