Марк Д. Фершильд. Модели цветового восприятия

Подождите немного. Документ загружается.

концепции ретинексной теории могут оказаться весьма полезными, к примеру:

сравнительно недавно ретинексные алгоритмы стали применять для компрес



сии динамического диапазона цифровых изображений и их цветокоррекции

(Джобсон и колл., 1997). Прочие сферы применения, претензии и успехи рети



нексной теории описаны МакКанном (1993).

Необходимость учета высшими моделями цветового восприятия пространст



венных размерностей в связке со спектральными — бесспорна, и концепции ре



тинексной теории дают нам некоторое понимание того, каким образом можно

обеспечить такой учет. В процессе развития находятся и иные подходы к теории

ретинексов (к примеру, Поирсон и Ванделл, 1993; Чанг и Ванделл, 1996), что го



товит почву для дальнейшего развития моделей хроматической адаптации.

Таким образом, фонкризовская модель — это прочный фундамент моделей

цветового восприятия, но для прогнозирования ряда феноменов адаптации он

нуждается в некотором укреплении.

О пространственных моделях хроматической адаптации и моделях воспри



ятия изображений мы будем подробно говорить в 20й главе.

9.3 МОДЕЛЬ НАЯТАНИ

Одним из важных расширений фонкризовской гипотезы является нелиней

ная модель хроматической адаптации, разработанная научной командой На

ятани. Данная модель была создана на основе т.н. фоновой колориметрии (рас

ширение CIEтрехстимульной колориметрии), лежащей в сфере интересов све

тотехники. Исток модели — в исследованиях МакАдама (1961).

Модель Мак;Адама

В 1961 г. МакАдам описал нелинейную модель хроматической адаптации,

в которой колбочковые ответы были выражены как некая постоянная в сово



купности с коэффициентом усиления колбочкового возбуждения, растущим по

некоей степенной зависимости. Данная модель представляет собой результат

эмпирической подгонки данных о хроматической адаптации, ранее получен



ных МакАдамом (1956). Интересно, что МакАдаму потребовалась условная

зрительная система с колбочками пяти типов, дабы истолковать эксперимен



тальные данные в линейном виде (вероятно, так получилось потому, что

МакАдам использовал технику ассиметричных соответствий, при которой две

разных области сетчатки [левая и правая половины] экспонировались различ



ными адаптирующими стимулами). Нелинейная модель МакАдама дает хоро



шее приближение к экспериментальным данным и является предшественни



ком сегодняшних нелинейных моделей.

Модель Наятани

Нелинейная модель научной группы Наятани (1980, 1981) начинается

с управления усилением, идущим по степенной функции с вариабельным зна



чением степени. В этой модели фонкризовские коэффициенты пропорциональ



209

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

ны максимумам длинно, средне и коротковолновых колбочковых ответов

и степень функции зависит от фотометрической яркости адаптирующего поля.

Напомним, что нелинейная функция была заявлена в классической работе

Стивенсов (1963), посвященной субъективной яркости.

Другой интересной и важной особенностью нелинейной модели является до



бавка к колбочковым ответам понятия «шум», что позволяет моделировать по



роговое поведение зрительной системы.

В общем виде модель выражается уравнениями 9.12–9.14:

(9.12)

(9.13)

(9.14)

где L

, M

и S

— колбочковые сигналы после адаптации; L, M и S—колбочко

вые возбуждения; L

, M

и S

— шум; L

, M

и S

— колбочковые возбуждения

по адаптирующему полю; b

, b

и b

— степени монотонно растущих функций

соответствующих колбочковых возбуждений по адаптирующему полю (кон

кретные величины степеней можно найти у Наятани [1982]); a

иa

— коэф

фициенты, заданные тем принципом, что точное цветовое постоянство немар

кированного манселловского образца сохраняется, если его коэффициент яр

кости равен коэффициенту яркости адаптирующего фона.

Такахама (1984) расширил модель Наятани до уровня прогнозирования со

гласованных цветовых стимулов при фонах с различными коэффициентами

яркости. Версия модели от 1987 г. (Наятани, 1987) была принята CIE в качест



ве пробной: предполагалось, что CIE, действуя через свои технические комите



ты, соберет дополнительные данные для тестирования и возможного улучше



ния модели Наятани и решит вопрос о том, рекомендовать ли данную модель

для общего пользования. Результаты тестирования оказались неубедительны



ми, поэтому CIE не приняла модель в качестве кандидата на международный

стандарт. Тонкости модели и ее полная формулировка были отработаны в ис



пытательный период и подытожены в техническом отчете CIE (CIE 1994).

Нелинейная модель Наятани использовалась для прогнозирования брене



мановских согласованных стимулов; результаты, аналогичные результатам

фонкризовской модели (рис. 9.2), представлены на рис. 9.3: предикторы весь



ма хороши, но все же несколько менее точны, чем у простой фонкризовской мо



дели (по тем же данным).

Одна из причин такой ситуации состоит в том, что бренемановские данные

были собраны в таких условиях просмотра, при которых отсутствовал эффект

когнитивного обесцвечивания осветителя, поэтому хроматическая адаптация

была неполной и бренемановское адаптирующее поле, построенное на свете

210

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

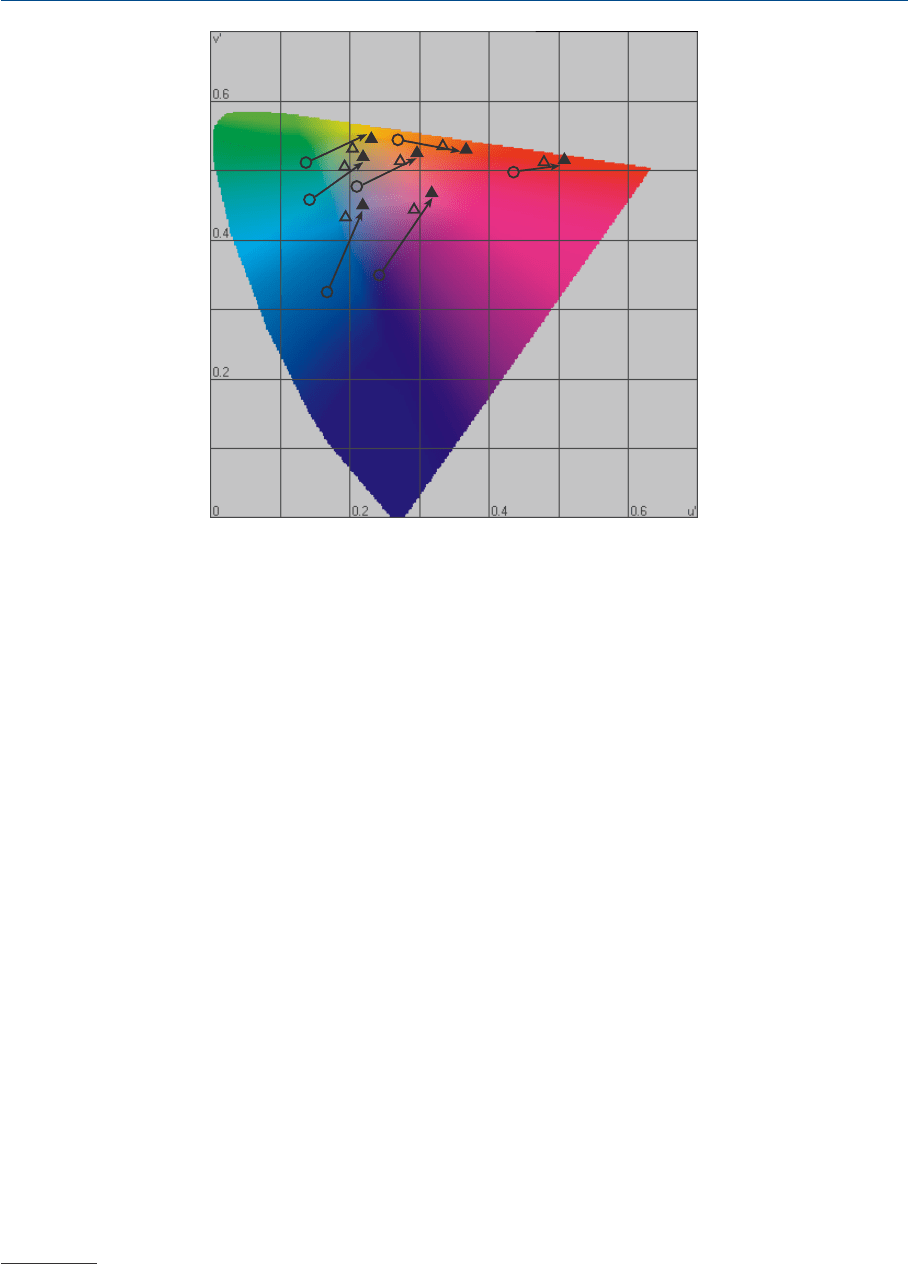
ламп накаливания, по ощущению оставалось желтоватым. В результате кон

трольные визуальные данные оказались сдвинутыми в желтую сторону относи

тельно всех предикторов модели Наятани. Сравнительно недавно (Наятани,

1997) появились усовершенствованные методы определения и учета степени

хроматической адаптации в научных экспериментах.

Нелинейная модель Наятани способна прогнозировать эффекты Ханта (рост

полноты цвета по мере роста адаптирующей яркости), Стивенса (рост светлот



ного контраста по мере роста яркости) и Хельсона — Джадда (появление цвето



вого тона у немаркированных манселловских образцов при резкохроматичном

освещении). Стоит отметить, что фонкризовский расчет смены хроматической

адаптации не зависит от яркости и, таким образом, не может быть использован

для прогноза тех феноменов восприятия, которые являются функцией от нее.

Плюс к тому, линейный характер простого фонкризовского расчета препятст



вует прогнозу эффекта Хельсона — Джадда.

Модель Наятани интересна по ряду причин. Она весьма простым путем со



вершенствует фонкризовскую гипотезу, поднимая ее на уровень, при котором

модель становится способной к прогнозу некоторых дополнительных эффек



тов. Также модель Наятани оказала серьезное влияние на работу CIE в области

моделирования хроматической адаптации и цветового восприятия в целом, что

заложило базис одной из двух существующих сегодня полноценных моделей

цветового восприятия

211

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

Рис. 9.3 Предикторы некоторых согласованных цветовых стимулов, полученные при помощи

нелинейной модели Наятани. Полые треугольнички представляют визуальные данные;

сплошные треугольнички — предикторы модели.

Здесь автор намекает на модели CIECAM97s и CIECAM02, утвержденные CIE. — Прим. пер.

Полная модель цветового восприятия, разработанная Наятани, описана

в 11й главе.

9.4 МОДЕЛЬ ГУТА

В науке о зрении (но не в колориметрии) популярна одна из вариаций моде



ли Наятани — модель, описанная Гутом (1991, 1995).

Гутовская модель не имеет прямого отношения к трехстимульной колори



метрии CIE, поскольку колбочковые чувствительности не представлены в виде

линейной трансформации CIEфункций цветового соответствия. Последнее

создает определенные трудности в реализации модели. В прикладном плане

было бы разумно (и, конечно, очень полезно в плане прогнозов) поступить ина



че: использовать набор колбочковых чувствительностей, получаемых непо



средственно из трехстимульных значений CIE, но при этом с добавкой гутов



ской формулировки.

Гутовская модель — это фрагмент зрительной модели ATD (см. гл. 14), соз



данной в результате многолетних усилий по согласованию прогнозов с данны



ми визуальных экспериментов. Большинство этих экспериментов вместо шка

лирования по размерностям цветового восприятия (см. гл. 4) основаны на клас

сической пороговой психофизике.

В общем виде гутовская модель хроматической адаптации дана в уравнени

ях 9.15–9.20:

LL L L

rr ra

=- +[( /( ))]1

(9.15)

=+0 66 0 002

(9.16)

MM M M

rr ra

=- +[ ( / ( ))]1

(9.17)

=+10 0 003

(9.18)

SS S S

rr ra

=- +[( /( ))]1

(9.19)

=+0 45 0 00135

(9.20)

где L

, M

и S

— колбочковые сигналы после адаптации; L, M и S—колбочко



вые возбуждения; L

, M

и S

— колбочковые возбуждения по адаптирующему

полю после нелинейной компрессии; s — некая постоянная (номинально равная

300), о которой обычно говорят как о шумовом факторе. Важно отметить также,

что колбочковые ответы в данной модели должны быть выражены в абсолютных

единицах, поскольку уровень фотометрической яркости никак не учитывается.

Взаимоотношения гутовской модели с фонкризовской можно выразить с по



мощью некоей математической манипуляции: если проигнорировать изна



212

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

чальную нелинейность, фонкризовский коэффициент усиления для гутовской

модели может быть выведен из уравнения 9.15 по формуле 9.21:

kL L

Lr r

=- +1

(/( ))s

(9.21)

Взаимоотношения гутовской модели с традиционными фонкризовскими

коэффициентами становятся понятными, если выполнить алгебраическую за



мену согласно уравнениям 9.22–9.24:

kL LL L

Lr rr r

=+ + - +()/()/()ss s

0000

(9.22)

kLL L

Lrr r

=+ - +()/()ss

00 0

(9.23)

=+ss/( )

(9.24)

Собственно говоря, разница между моделями заключена в «s», о которой,

напомним, говорят как о шумовом факторе, играющем важную роль при ма



лых интенсивностях стимулов и не столь значимом при больших. Таким обра



зом, если уровень яркости растет, модель Гута все более и более походит на но



минальную фонкризовскую модель.

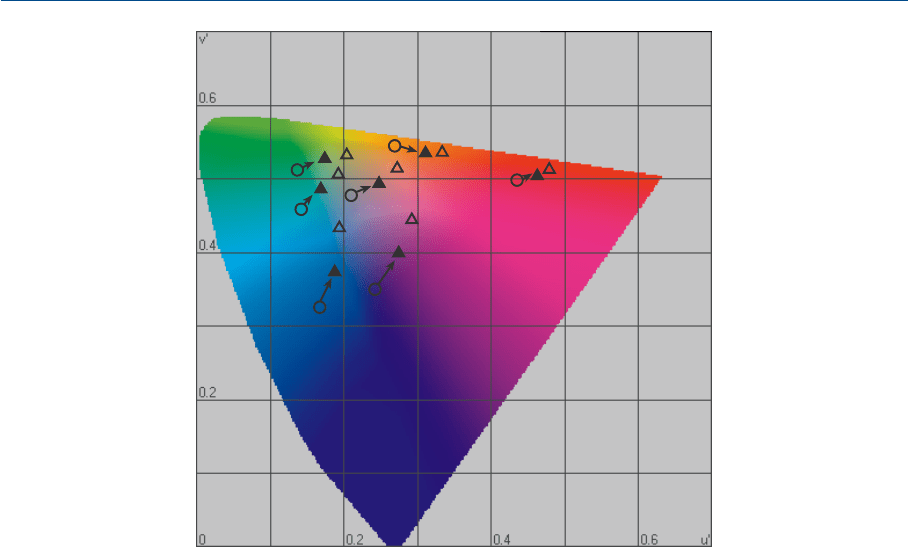
На рис. 9.4 показаны бренемановские согласованные цветовые стимулы (вы



213

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

Рис. 9.4 Предикторы некоторых согласованных цветовых стимулов, полученные с помощью

модели Гута. Полые треугольнички представляют визуальные данные; сплошные треуголь

нички — предикторы модели.

числения предикторов были выполнены по номинальной, открыто опублико



ванной гутовской модели): мы видим, что имеет место систематический разброс

между визуальными данными и их предикторами. Данный разброс можно от



следить по sпараметру: с одной стороны, мы знаем, что бренемановские данные

великолепно прогнозируются простой фонкризовской моделью; с другой сторо



ны, при уменьшении sпараметра предикторы гутовской модели улучшаются,

следовательно, мы можем говорить об определенной ущербности модели Гута.

В то же время, в качестве структуры общей зрительной модели, гутовская

модель вполне способна к удовлетворительному прогнозированию визуальных

данных, однако для разных условий просмотра и разных визуальных экспери



ментов она зачастую требует малых значений в управлении своими параметра



ми, что вполне пригодно при попытках прогнозирования различных феноме



нов зрительного восприятия, но совершенно непрактично в большинстве при



кладных сфер, таких, как репродуцирование на разных носителях (где конеч



ные условия просмотра зачастую неизвестны и поэтому нет никакой возможно



сти выполнить серию итераций). Таким образом, для использования гутовской

модели адаптации (а также полной ATDмодели, описанной в 14й главе) в при

кладных сферах потребуются определенные разъяснения.

9.5 МОДЕЛЬ ФЕРШИЛЬДА

Бренемановские результаты, демонстрирующие неполноту хроматической

адаптации, подтолкнули исследователей к проведению серии экспериментов

(Фершильд, 1990), целью которых было выявление степени хроматической

адаптации к стимулам различных видов. Данная работа привела к очередной

модификации фонкризовской гипотезы, которая обрела способность прогнози

ровать степень адаптации, основываясь непосредственно на адаптирующем

стимуле (Фершильд, 1991).

Данная модель, подобно модели Наятани, полностью совместима с CIE

колориметрией, но ориентирована скорее на науку об изображениях, нежели

на светотехнику. Модель сконструирована так, чтобы, с одной стороны, быть

простой в обращении, а с другой — включать в себя и когнитивное обесцвечива



ние осветителя, и эффект Ханта, и неполноту хроматической адаптации.

Яснее всего модель формулируется в виде серии матричных преобразований.

Первый шаг — это преобразование CIEтрехстимульных значений XYZ

в фундаментальные трехстимульные значения LMS для первых условий про



смотра, что показано в уравнениях 9.25–9.26 (преобразование Ханта — Поин



тера — Эстевец с нормировкой на D65осветитель):

= M

(9.25)

214

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

M =

0 4002 0 7076 0 0808

02263 11653 00457

00 00 091

.. .

...

(9.26)

Следующий шаг — применение модифицированного фонкризовского расчета

смены хроматической адаптации, учитывающего неполноту последней (урав



нения 9.27–9.31):

(9.27)

A =

00 00

(9.28)

(9.29)

()

(/)

(9.30)

LL MM SS

EEE

3( / )

///

nnn

(9.31)

где Y

— это фотометрическая яркость адаптирующего стимула в cd/m

(под



строчные индексы n относятся к адаптирующему стимулу, а подстрочные ин



дексы E — к равноэнергетическому осветителю); степень u равна 1/3.

Переменные p и a для коротко (S) и длинно (L) волновых колбочковых чув



ствительностей рассчитываются аналогичным образом.

Уравнения неполной хроматической адаптации основаны на аналогичных

уравнениях хантовской модели цветового восприятия (Хант, 1991), которая

подробно описана в гл. 12. (Хант никогда не публиковал схему расчета смены

хроматической адаптации вне контекста своей модели цветового восприятия,

поэтому хантовская модель всегда рассматривается целиком [см. гл. 12]).

Переменные a — это модифицированные фонкризовские коэффициенты;

переменные p представляют долю от полной фонкризовской адаптации и, когда

адаптация неполна, не равны единице; pзначения зависят от яркости адапти



рующего стимула и его цвета: если яркость растет — степень полноты адапта



ции выше, если цветность адаптирующего стимула удаляется от нормальной

точки (равноэнергетический осветитель) — степень адаптации снижается. Ко



215

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

гда происходит когнитивное обесцвечивание осветителя, переменные p

, p

и p

равны единице.

Уравнения 9.30 и 9.31 реализуют данный механизм внутри модели, и выда



ваемые им предикторы вполне адекватны визуальным экспериментальным

данным (Хант и Виннер, 1975; Бренеман, 1987; Фершильд, 1992).

Завершающим шагом в вычислении постадаптационных сигналов является

преобразование, которое по уравнениям 9.32–9.34 позволяет рассчитать

яркостнозависимое взаимодействие между колбочками трех типов:

(9.32)

C =

(9.33)

cY=-0219 0 0784

..log()

(9.34)

Переменная с, известная как «цепная модель», взята из работы Такахамы

(1977). В этой модели, от которой в дальнейшем Такахама отказался, отдав

предпочтение нелинейной модели (Наятани, 1981), переменные взаимодейст

вия были введены для прогнозирования яркостнозависимых эффектов. С той

же целью Сматрица была включена и в модель Фершильда.

Для определения цветностей согласованных стимулов по вторым адапти



рующим условиям, для них должны быть получены матрицы «А» и «С», затем

инвертированы и применены согласно уравнениям 9.35–9.37:

–1

(9.35)

–1

(9.36)

= M

–1

(9.37)

216

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

Результирующую модель можно выразить в виде отдельного матричного

уравнения (9.38):

= MACCAM

–1

(9.38)

Дальнейшие эксперименты (к примеру, Пиротта и Фершильд, 1995) показа



ли, что Сматрица создавала дополнительную нежелательную зависимость от

яркости, что приводило к общему сдвигу светлоты. Данный сдвиг не оказывал

влияния на качество репродуцирования изображений, поскольку сдвигалось

все изображение целиком. Однако матрица вводила серьезную систематиче



скую ошибку в предикторы цветов простых объектов

. В итоге модель была пе



ресмотрена (Фершильд, 1994) и Сматрица исключена из нее. Прогнозы по про



стым цветам улучшились, а на изображения удаление матрицы не оказало

влияния. Правда, при этом модель перестала прогнозировать эффект Ханта, но

в работе с изображениями такая потеря некритична, поскольку в этом случае

любым прогнозам хантовского эффекта всегда противостоит гамут мэппинг.

Данные изменения, наряду с некоторыми упрощениями в уравнениях (раз

личные нормировки), были объединены и заложены в основу последней версии

RLABмодели цветового восприятия, описанной в 13й главе (Фершильд, 1996).

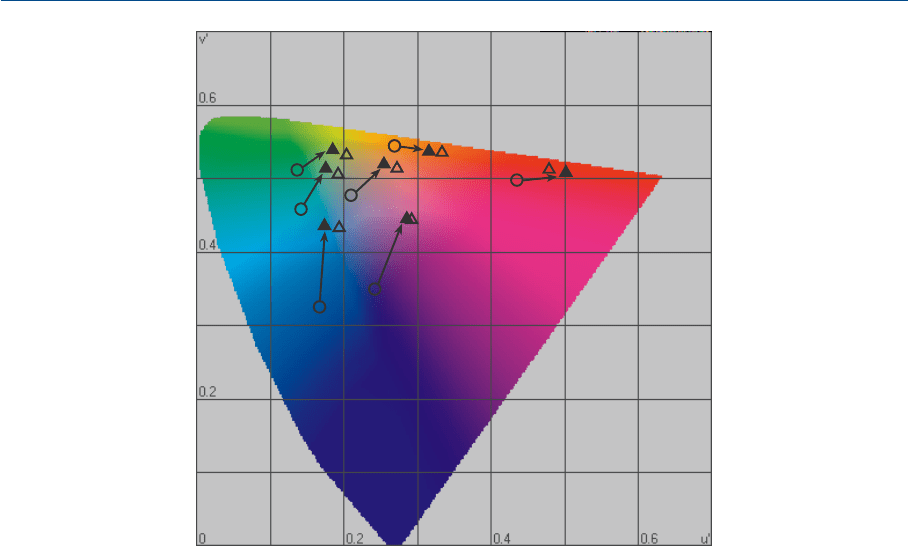
На рис. 9.5 показаны предикторы бренемановских согласованных цветовых

стимулов, выполненные по фершильдовской модели смены хроматической

адаптации. Предикторы, выдаваемые обеими вышеописанными версиями мо

дели (оригинальной и упрощенной), идентичны и не менее (если не более) хоро

ши, чем предикторы всех описанных выше моделей. Количественный анализ

всех бренемановских данных подтверждает этот результат (Фершильд, 1991).

9.6 СЕМЕЙСТВО CAT;МОДЕЛЕЙ

В 1998 г. CIE приняла модель цветового восприятия CIECAM97s (описана

в гл. 15), которая задействует модифицированный вариант расчета смены хро



матической адаптации, известный как «Брэдфорское преобразование». По

сути Брэдфордская трансформация — это фонкризовский расчет плюс допол



нительная степенная нелинейность по синему каналу плюс оптимизированные

колбочковые чувствительности. Нелинейность по синему каналу создает ряд

практических проблем в плане инверсии CIECAM97sмодели, поэтому акцент

был сделан на простых, линейных, расчетах смены хроматической адаптации

(CAT), построенных путем оптимизации матричного преобразования XYZ

в RGBзначения, выполняемого до фонкризовской нормировки.

Фершильд (2001) опубликовал обзор линейных CAT, предназначенных для

пересмотра CIECAM97s и перехода к CIECAM02 (см. гл. 16): для получения оп



тимальной матрицы в расчетах были задействованы различные методики, но

217

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

Имеются в виду единичные (изолированные) цветовые стимулы. — Прим. пер.

все они давали несколько разные предикторы и у каждой были свои преимуще

ства и недостатки. Однако оптимальная схема линейного матричного преобра

зования все же была найдена, и результаты (по всем доступным данным) оказа

лись так же хороши, что и у нелинейной CAT, включенной в CIECAM97s. Столь

удачный исход привел к созданию и утверждению техническим комитетом CIE

(CIE TC801) модели цветового восприятия CIECAM02, использующей линей



ную CAT.

Решение TC801 принять к использованию линейную CAT было принято

легко — куда более трудным оказался выбор оптимального матричного преоб



разования. Матрицыкандидаты были весьма схожи друг с другом, и их расчет



ные чувствительности (по сравнению с истинными колбочковыми чувстви



тельностями) получились с более острыми пиками, а сами пики оказались

сильнее разнесены по спектру — но при этом в них появились отрицательные

значения. Физиологическая достоверность простого фонкризовского расчета

при такой оптимизации оказалась под большим вопросом, но зато модели смог



ли с большей точностью прогнозировать соответствия, приняв весь объединен



ный механизм адаптации зрительной системы человека за «черный ящик».

Предикторы, рассчитанные по фонкризовской модели с использованием

«заостренных» чувствительностей, имели тенденцию к большей цветовой кон



стантности, нежели предикторы, полученные с использованием истинных кол



бочковых чувствительностей. Прогноз, выполненный на основе повышенной

цветовой константности, призван имитировать результат работы высокоуров



невых механизмов адаптации.

218

ГЛАВА 9 МОДЕЛИ ХРОМАТИЧЕСКОЙ АДАПТАЦИИ

Рис. 9.5 Предикторы некоторых согласованных цветовых стимулов, полученные с помощью

модели Фершильда (1991). Полые треугольнички представляют визуальные данные; сплош

ные треугольнички — предикторы модели.