Marathe K. Topics in Physical Mathematics

Подождите немного. Документ загружается.

348 10 3-Manifold Invariants

amplitude in terms of parameters λ and τ , which are deﬁned in terms of the

Chern–Simons parameters by

λ =

2π

k + n

,τ= nλ =

2πn

k + n

. (10.70)

The parameter λ is the string coupling constant and τ is the ’t Hooft cou-

pling nλ of the Chern–Simons theory. The parameter τ entering in the string

amplitude expansion has the geometric interpretation as the K¨ahler modulus

of a blown up S

in the resolved M

.IfF

(τ) denotes the amplitude for a

closed string at genus g then we have

(τ)=

∞



h=1

(g,h)

. (10.71)

So summing over the holes amounts to ﬁlling them up to give the closed

string amplitude.

The large n expansion of T in terms of parameters λ and τ is given by

T =exp



−

∞



g=0

2g−2

(τ)



, (10.72)

where F

deﬁned in (10.71) can be interpreted on the string side as the

contribution of closed genus g Riemann surfaces. For g>1theF

can be

expressed in terms of the Euler characteristic χ

and the Chern class c

g−1

the Hodge bundle over the moduli space M

of Riemann surfaces of genus g

as follows:



g−1

−

(2g − 3)!

∞



n=1

2g−3

−n(τ )

. (10.73)

The integral appearing in the formula for F

can be evaluated explicitly to

give



g−1

(−1)

(g−1)

(2π)

(2g−2)

2ζ(2g − 2)χ

. (10.74)

The Euler characteristic is given by the Harer–Zagier [185]formula

(−1)

(g−1)

(2g)(2g − 2)

, (10.75)

where B

is the (2g)th Bernoulli number. We omit the special formulas

for the genus 0 and genus 1 cases. The formulas for F

for g ≥ 0coincide

with those of the g-loop topological string amplitude on a suitable Calabi–

Yau manifold. The change in geometry that leads to this calculation can be

thought of as the result of coupling to gravity. Such a situation occurs in the

quantization of Chern–Simons theory. Here the classical Lagrangian does not

10.8 Chern–Simons and String Theory 349

depend on the metric; however, coupling to the gravitational Chern–Simons

term is necessary to make it a TQFT.

We have mentioned the following four approaches that lead to the WRT

invariants:

1. Witten’s TQFT calculation of the Chern–Simons partition function;

2. Quantum group (or Hopf algebraic) computations initiated by Reshetikhin

and Turaev;

3. Kohno’s special functions corresponding to representations of mapping

class groups in the space of conformal blocks and a similar approach by

Crane;

4. open or closed string amplitudes in suitable Calabi–Yau manifolds.

These methods can also be applied to obtain invariants of links, such as the

Jones polynomial. Indeed, this was the objective of Witten’s original work.

WRT invariants were a byproduct of this work. Their relation to topological

strings came later.

The WRT to string theory correspondence was extended by Gopakumar

and Vafa (see hep-th/9809187, 9812127) by using string theoretic arguments

to show that the expectation value of the quantum observables deﬁned by

the Wilson loops in the Chern–Simons theory has a similar interpretation

in terms of a topological string amplitude. This led them to conjecture a

correspondence exists between certain knot invariants (such as the Jones

polynomial) and Gromov–Witten type invariants of generalized Calabi–Yau

manifolds. Gromov–Witten invariants of a Calabi–Yau 3-fold X,areingen-

eral, rational numbers, since one has to get the weighted count by dividing

by the order of automorphism groups. Using M-theory Gopakumar and Vafa

argued that the generating series F

of Gromov–Witten invariants in all de-

grees and all genera is determined by a set of integers n(g, β). They give the

following remarkable formula for F

(λ, q)=



g≥0



k≥1

n(g, β)(2 sin(kλ/2))

2g−2

kβ

where λ is the string coupling constant and the ﬁrst sum is taken over all

nonzero elements β in H

(X). We note that for a ﬁxed genus there are only

ﬁnitely many nonzero integers n(g,β). A mathematical formulation of the

Gopakumar–Vafa conjecture (GV conjecture) is given in [312]. Special cases

of the conjecture have been veriﬁed (see, for example, [313] and references

therein). In [251] a new geometric approach relating the Gromov–Witten

invariants to equivariant index theory and 4-dimensional gauge theory was

used to compute the string partition functions of some local Calabi–Yau

spaces and to verify the GV conjecture for them.

A knot should correspond to a Lagrangian D-brane on the string side and

the knot invariant would then give a suitably deﬁned count of compact holo-

morphic curves with boundary on the D-brane. To understand a proposed

350 10 3-Manifold Invariants

proof, recall ﬁrst that a categoriﬁcation of an invariant I is the construction of

a suitable homology such that its Euler characteristic equals I.Awellknown

example of this is Floer’s categoriﬁcation of the Casson invariant. We will dis-

cuss in Chapter 11 Khovanov’s categoriﬁcation of the Jones polynomial V

(q)

by constructing a bi-graded sl(2)-homology H

i,j

determined by the knot κ.

Its quantum or graded Euler characteristic equals the Jones polynomial, i.e.,

(q)=



i,j

(−1)

dim H

i,j

Now let L

be the Lagrangian submanifold corresponding to the knot κ of a

ﬁxed Calabi–Yau space X.Letr be a ﬁxed relative integral homology class of

the pair (X, L

). Let M

g,r

denote the moduli space of pairs (Σ

,A), where

is a compact Riemann surface in the class r with boundary S

and A is a

ﬂat U (1) connection on Σ

. These data together with the cohomology groups

g,r

) determine a tri-graded homology. It generalizes the Khovanov ho-

mology. Its Euler characteristic has a physical interpretation as a generating

function for a class of invariants in string theory and these invariants can be

used to obtain the Gromov–Witten invariants. Taubes has given a construc-

tion of the Lagrangians in the Gopakumar–Vafa conjecture. We note that

counting holomorphic curves with boundary on a Lagrangian manifold was

introduced by Floer in his work on the Arnold conjecture. The tri-graded

homology is expected to unify knot homologies of the Khovanov type as well

as knot Floer homology constructed by Ozsw´ath and Szab´o[309], which pro-

vides a categoriﬁcation of the Alexander polynomial. Knot Floer homology

is deﬁned by counting pseudo-holomorphic curves and has no known com-

binatorial description. An explicit construction of a tri-graded homology for

certain torus knots was recently given by Dunﬁeld, Gukov, and Rasmussen

[math.GT/0505662].

Chapter 11

Knot and Link Invariants

11.1 Introduction

In this chapter we make some historical observations and comment on some

early work in knot theory. Invariants of knots and links are introduced in

Section 11.2. Witten’s interpretation of the Jones polynomial via the Chern–

Simons theory is discussed in Section 11.3. A new invariant of 3-manifolds is

obtained as a byproduct of this work by an evaluation of a certain partition

function of the theory. We already met this invariant, called the Witten–

Reshetikhin–Turaev (or WRT) invariant in Chapter 10. In Section 11.4 we

discuss the Vassiliev invariants of singular knots. Gauss’s formula for the

linking number is the starting point of some more recent work on self-linking

invariants of knots by Bott, Taubes, and Cattaneo. We will discuss their

work in Section 11.5. The self-linking invariants were obtained earlier by

physicists using Chern–Simons perturbation theory. This work now forms a

small part of the program initiated by Kontsevich [235] to relate topology

of low-dimensional manifolds, homotopical algebras, and non-commutative

geometry with topological ﬁeld theories and Feynman diagrams in physics.

See also the book [176] by Guadagnini. Khovanov’s categoriﬁcation of the

Jones polynomial by Khovanov homology is the subject of Section 11.6. We

would like to remark that in recent years many applications of knot theory

have been made in chemistry and biology (for a brief of discussion of these

and further references see, for example, [260]). Some of the material in this

chapter is from my article [263]).

In the second half of the nineteenth century a systematic study of knots

in R

was made by Tait. He was motivated by Kelvin’s theory of atoms

modeled on knotted vortex tubes of ether. It was expected that physical and

chemical properties of various atoms could be expressed in terms of properties

of knots such as the knot invariants. Even though Kelvin’s theory did not

hold up, the theory of knots grew as a subﬁeld of combinatorial topology. Tait

classiﬁed the knots in terms of the crossing number of a regular projection.

K. Marathe, Topics in Physical Mathematics, DOI 10.1007/978-1-84882-939-8 11, 351

 Springer-Verlag London Limited 2010

352 11 Knot and Link Invariant s

A regular projection of a knot on a plane is an orthogonal projection

of the knot such that at any crossing in the projection exactly two strands

intersect transversely. Tait made a number of observations about some general

properties of knots which have come to be known as the “Tait conjectures.” In

its simplest form the classiﬁcation problem for knots can be stated as follows.

Given a projection of a knot, is it possible to decide in ﬁnitely many steps

if it is equivalent to an unknot? This question was answered aﬃrmatively by

Haken [182] in 1961. He proposed an algorithm that could decide if a given

projection corresponds to an unknot. However, because of its complexity the

algorithm has not been implemented on a computer even after a half century.

We add that in 1974 Haken and Appel solved the famous four-color problem

for planar maps by making essential use of a computer program to study the

thousands of cases that needed to be checked. A very readable, non-technical

account of their work can be found in [12].

11.2 Inv ariants of Knots and Links

Let M be a closed orientable 3-manifold. A smooth embedding of S

in M is

called a knot in M.Alink in M is a ﬁnite collection of disjoint knots. The

number of disjoint knots in a link is called the number of components of the

link. Thus, a knot can be considered a link with one component. Two links

L, L



in M are said to be equivalent if there exists a smooth orientation-

preserving automorphism f : M → M such that f (L)=L



. For links with

two or more components we require f to preserve a ﬁxed given ordering of

the components. Such a function f is called an ambient isotopy and L and



are called ambient isotopic. Ambient isotopy is an equivalence relation on

the set of knots in M, and the equivalence class [κ]ofaknotκ under this

relation is called the isotopy class of κ.Ifh : S

→ M is a knot, then its

image κ = h(S

) is also called a knot. A knot type [κ]ofaknotκ is deﬁned

to be the isotopy class of κ. As in all classiﬁcation problems we try to ﬁnd a

set of invariants of knots that will distinguish diﬀerent knot types. However,

at this time no such set of invariants of knots is known. Another approach is

to deﬁne a suitable “energy” functional on the space of knots and study the

critical points of its gradient ﬂow to identify the knot type of a given knot.

Even though there are several candidates for energy functional there is no

known example which produces an energy minimizer for every knot type.

Knots and links in R

can also be obtained by using braids. A braid on

n strands (or with n strings, or simply an n-braid) can be thought of as a

set of n pairwise disjoint strings joining n distinct points in one plane with n

distinct points in a parallel plane in R

. Making a suitable choice of planes

and points we make the following deﬁnition.

Deﬁnition 11.1 Fix a number n ∈ N and let i be an integer such that

1 ≤ i ≤ n.LetA

(resp., B

) denote the point in R

with x-coordinate i lying

11.2 Invariants of Knots and Links 353

on the x-axis (resp., line y =0, z =1). Let σ ∈ S

, the symmetric group

on the ﬁrst n natural numbers. A strand from A

to B

σ(i)

is a smooth curve

from A

to B

σ(i)

such that the z coordinate of a point on the curve decreases

monotonically from 1 to 0 as it traces out the curve from A

to B

σ(i)

set of n non-intersecting strands from A

to B

σ(i)

, 1 ≤ i ≤ n,iscalledan

n-braid in standard form. Two n-braids are said to be equivalent if they are

ambient isotopic. The set of equivalence classes of n-braids is denoted by B

It is customary to call an element of B

also an n-braid. It is clear from

the context whether one is referring to an equivalence class or its particular

representative.

The multiplication operation on B

is induced by concatenation of braids.

If A

(resp., A



) are the endpoints of braid b

(resp., b

) then the braid

is obtained by gluing the ends B

of b

to the starting points A



of b

This can be put in the standard braid form going from z =1toz =0by

reparametrization so that b

runs from z =1toz =1/2andb

runs from

z =1/2toz = 0. A representative of the unit element is the braid consisting

of n parallel strands from A

to B

,1≤ i ≤ n. Taking the mirror image of

in the plane z = 0 gives a braid equivalent to b

−1

(its parallel translation

along the z-axis by 1 puts it in the standard form. A nontrivial braid has

at least two strands joining A

and B

for i = j.Foreachi with 1 ≤ i<n

let σ

be an n-braid with a strand from A

to B

i+1

crossing over the strand

from A

i+1

to B

and with vertical strands from A

to B

for j = i, i +1.

Then it can be shown that σ

and σ

are not equivalent whenever i = j and

that every n-braid can be represented as a product of braids σ

and σ

−1

for

1 ≤ i<n; i.e., the n − 1braidsσ

generate the braid group B

.Analysis

of the equivalence relation on braids leads to the relations

i+1

= σ

i+1

, 1 ≤ i ≤ n − 2. (11.1)

Equation (11.1) is called the braid relation,and.

= σ

, 1 ≤ i, j ≤ n − 1and|i − j| > 1 (11.2)

is called the far commutativity relation, for it expresses the fact that the

generators σ

,σ

commute when the indices i, j are not immediate neighbors.

This discussion leads to the following well-known theorem of M. Artin.

Theorem 11.1 The set B

with multiplication operation induced by concate-

nation of braids is a group generated by the elements σ

, 1 ≤ i ≤ n−1 subject

to the braid relations (11.1) and the far commutativity relations (11.2).

The braid group B

is the inﬁnite cyclic group generated by σ

and hence

is isomorphic to Z.Forn>2 the group B

contains a subgroup isomorphic

to the free group on two generators and is therefore, non-Abelian. The group

is related to the modular group PSL(2, Z) in the following way. It is easy

to check that the elements a = σ

, b = σ

generate B

and that the

element c = a

= b

generates its center Z(B

). Let f : B

→ SL(2, Z)be

354 11 Knot and Link Invariant s

the mapping deﬁned by

f(a):=



−10



,f(b):=



−11



One can show that f is a surjective homomorphism that maps c to −I

where I

is the identity element. Let

f = π ◦ f,whereπ is the canonical

projection of SL(2, Z)toPSL(2, Z). Then

f : B

→ PSL(2, Z)isalsoa

surjective homomorphism with kernel the center Z(B

). Thus, B

/Z (B

)is

isomorphic to the modular group PSL(2, Z).

The map that sends the braid σ

to the transposition (i, i +1) in the

symmetric group S

on n letters induces a canonical map π : B

→ S

.The

kernel, P

ofthesurjectivemapπ is called the pure braid group on n

strands. Thus, we have an exact sequence of groups

1 → P

→ B

→ S

→ 1,

where 1 denotes the group containing only the identity element. Braid groups

can also be deﬁned in terms of conﬁguration spaces. Recall that the conﬁgura-

tion space of n points in R

is the space of unordered sequences of n pairwise

distinct points. It is denoted by C

). General discussion of conﬁguration

spaces is given later in this chapter in deﬁning self-linking invariants. Each

braid b ∈B

deﬁnes a homotopy class of loops in this space. In fact, we

have an isomorphism of B

with the fundamental group π

)) of the

conﬁguration space C

). The group B

is also isomorphic to the mapping

class group of the unit disk in R

= C with n punctures or marked points.

Magnus pointed out that this interpretation of the braid group was known

to Hurwitz. Braids are implicit in his work on monodromy done in 1891.

However, they were deﬁned explicitly by E. Artin in 1925. Hurwitz’s inter-

pretation was rediscovered by Fox and Neuwirth in 1962. Birman’s book [40]

is a classic reference for this and related material. For an updated account,

see Kassel and Turaev [217].

Given an n-braid b with endpoints A

we can obtain a link by joining

each A

and B

by a smooth curve so that these n curves are non-intersecting

and do not intersect the strands of b. The resulting link is denoted by c(b)

and is said to be obtained by the operation of the closure of braid b.The

question whether every link in R

is the closure of some braid is answered

by the following classical theorem of Alexander.

Theorem 11.2 The closure map from the set of braids to the set of links

is surjective, i.e., any link (and, in particular, knot) is the closure of some

braid. Moreover, if braids b and b



are equivalent, then the links c(b) and c(b



)

are equivalent.

The minimum n such that a given link L is the closure of an n-braid is

called the braiding number or braid index of L and is denoted by b(L).

To answer the question of when the closure of a braid is a knot, we consider

11.2 Invariants of Knots and Links 355

the canonical homomorphism π : B

→ S

deﬁned above. The following

proposition characterizes when the closure of a braid is a knot.

Proposition 11.3 The closure c(b) of an n-braid b is a knot if and only if

the permutation π(b) has order n in the symmetric group S

In view of the above discussion it is not surprising that invariants of knots

and links should be closely related to representations of the braid group. The

earliest such representation was obtained in the 1930s by Burau. The Burau

representation is a matrix representation over the ring Z[t, t

−1

]ofLaurent

polynomials in t with integer coeﬃcients. We now indicate the construction

of the Burau representation of B

by matrices of order n. The representation

is trivial for n =1.Forn = 2 the generator σ

is mapped to the matrix

ˆσ

= U deﬁned by

U :=



1 −tt



For n>2 the generators σ

are mapped to the matrix ˆσ

with block diagonal

entries I

i−1

, U ,andI

n−i−1

,whereI

is the identity matrix of order k for

k =0andI

is regarded as the empty block and is omitted. For example,

the Burau representation of B

is deﬁned by

ˆσ

⎛

⎝

1 −tt0

010

001

⎞

⎠

, ˆσ

⎛

⎝

100

01− tt

010

⎞

⎠

It is a classical result that the Burau representation is faithful for n =

3. After extensive work by several mathematicians, it is now known that

the representation is not faithful for n>4. The case n = 4 is open as of

this writing. The Burau representation of B

can be used to construct the

Alexander polynomial invariant of the link obtained by the closure c(b)of

the braid b ∈B

. After nearly 60 years Jones obtained his link invariant

taking values in Laurent polynomials Z[t, t

−1

]int with integer coeﬃcients.

The new representations underlying his invariant are obtained by studying

certain ﬁnite-dimensional von Neumann algebras. A special case of these

representations was discovered earlier by Temperley and Lieb in their study of

certain models in statistical mechanics. Many surprising interpretations of the

Jones polynomial have been obtained using ideas coming from conformal ﬁeld

theory and quantum ﬁeld theory. Thus we have another example of a result

in physical mathematics. The Lawrence–Krammer–Bigelow representation of

the braid group is a matrix representation of B

over the ring of Laurent

polynomials Z[t, t

−1

,q,q

−1

]intwovariablest, q with integer coeﬃcients. This

representation is faithful for all n ≥ 1 and shows that the group B

is linear,

i.e., it admits an injective homomorphism into the general linear group over

Every link L in M has a tubular neighborhood N(L), which is the union

of smoothly embedded disjoint solid tori D

× S

, one for each component,

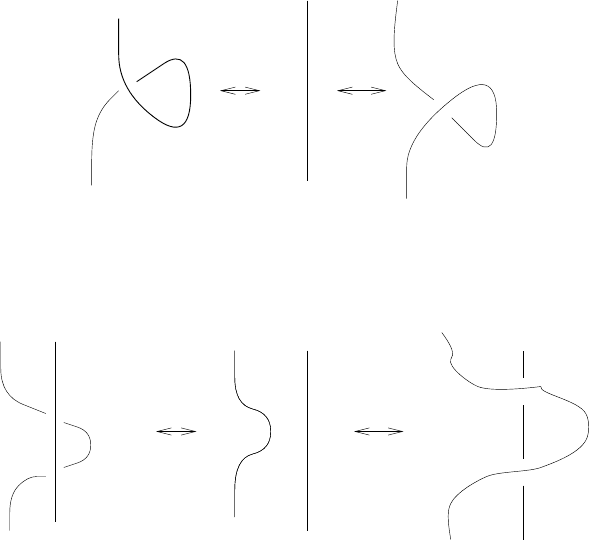
356 11 Knot and Link Invariant s

so that the cores {0}×S

of the tori form the given link L.ThesetN(L)

is called a thickening of L. Unless otherwise stated we shall take M to be

∼

∪{∞}and write simply a link instead of a link in S

. The diagrams

of links are drawn as links in R

. Every link L in S

or R

can be thickened.

A link diagram of L is a plane projection with crossings marked as over

or under. Two links are equivalent if a link diagram of one can be changed

into the given diagram of the other link by a ﬁnite sequence of moves called

the Reidemeister moves. There are three types of Reidemeister moves as

indicated in Figures 11.1, 11.2, and 11.3.

Fig. 11.1 Reidemeister mo ves of type I

Fig. 11.2 Reidemeister mo ves of type II

The simplest combinatorial invariant of a knot κ is the crossing number

c(κ). It is deﬁned as the minimum number of crossings in any projection of the

knot κ. The classiﬁcation of knots up to crossing number 17 is now known

[195]. The crossing numbers for some special families of knots are known;

however, the question of ﬁnding the crossing number of an arbitrary knot is

still unanswered. Another combinatorial invariant of a knot κ that is easy to

deﬁne is the unknotting number u(κ), the minimum number of crossing

changes in any projection of the knot κ thatmakesitintoaprojectionof

11.2 Invariants of Knots and Links 357

Fig. 11.3 Reidemeister mo ves of type III

the unknot. Upper and lower bounds for u(κ) are known for any knot κ.An

explicit formula for u(κ) for a family of knots called torus knots, conjectured

by Milnor nearly 40 years ago, has been proved recently by a number of

diﬀerent methods. The 3-manifold S

\κ is called the knot complement of

κ. The fundamental group π

\κ) of the knot complement is an invariant

of the knot κ. It is called the fundamental group of the knot (or simply the

knot group) and is denoted by π

(κ). Equivalent knots have homeomorphic

complements and conversely. However, this result does not extend to links.

A Seifert surface Σ

(or simply Σ) for a link L is a connected compact

orientable surface smoothly embedded in S

such that its boundary ∂Σ = L.

Theorem 11.4 Every link in S

bounds a Seifert surface.

The least genus of all Seifert surfaces of a given link L is called the genus

of the link L. For example, the genus of the unknot is 0.

We deﬁne an integer invariant of a knot κ, called the signature,byusing

its Seifert surface Σ

.Letα

,α

be two oriented simple loops on Σ

.Letα

be the loop obtained by moving α

away from Σ

along its positive normal in

. We can now associate an integer with the pair (α

,α

) to be the linking

number Lk(α

,α

). This induces a bilinear form on H

(Σ; Z). Let Q be the

matrix of this bilinear form with respect to some basis of H

(Σ; Z). Then the

signature sgn(κ)oftheknotκ is deﬁned to be the signature of the symmetric

matrix Q+ Q

. It can be shown that the signature of a knot is always an even

integer. In fact, sgn(κ)=2h(κ), where h(κ) is an integer-valued invariant of

the knot κ deﬁned by studying a special class of representations of the knot

group π

\ κ) into the group SU(2) along the lines of the construction of

the Casson invariant [253].

In the 1920s Alexander gave an algorithm for computing a polynomial

invariant Δ

(t) (a Laurent polynomial in t)ofaknotκ, called the Alexander

polynomial, by using its projection on a plane. He also gave its topological

interpretation as an annihilator of a certain cohomology module associated

to the knot κ. In the 1960s Conway deﬁned his polynomial invariant and

gave its relation to the Alexander polynomial. This polynomial is called the