Мангазеев П.В., Панков М.В., Кулагина Т.Е., Камартдинов М.Р. Гидродинамические исследования эксплуатационных и нагнетательных скважин. 2003 год
Подождите немного. Документ загружается.

Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
91
5.3 Вычисление производной
()
ii1
i
ii1
PP
Pt
ln t ln
t
−
−
−
′
≈
−
()
i1 i1
i
i1 i1
PP
Pt
ln t ln
t
+−
+
−
−
′
≈
−
()
i1 i
i
i1 i
PP
Pt
ln t ln
t
+
+
−
′
≈
−
ln t
P
• Чтобы посчитать значение логарифмической производной, необходимо
составить таблицу со значениями ln t
i
и P
i
и по формуле конечной разности
подсчитать значение производной в каждой точке t
i
:
5.3 Вычисление производной
-9.25278.490.74
1.38-9.2512.00278.860.70
7.5012.003.00278.380.66
-0.633.00-4.25278.260.62
0.87-4.256.00278.430.58
4.256.002.50278.190.54
5.002.507.50278.090.50
6.257.505.00277.790.46
3.885.002.75277.590.42
5.002.757.25277.480.38
13.887.2520.50277.190.34
8.3820.50-3.75276.370.30
12.25-3.7528.25276.520.26
23.1228.2518.00275.390.22
33.0018.0048.00274.670.18
48.00272.750.14
централь
ная
разность
правая
разность
левая
разность
P
i
ln t
i
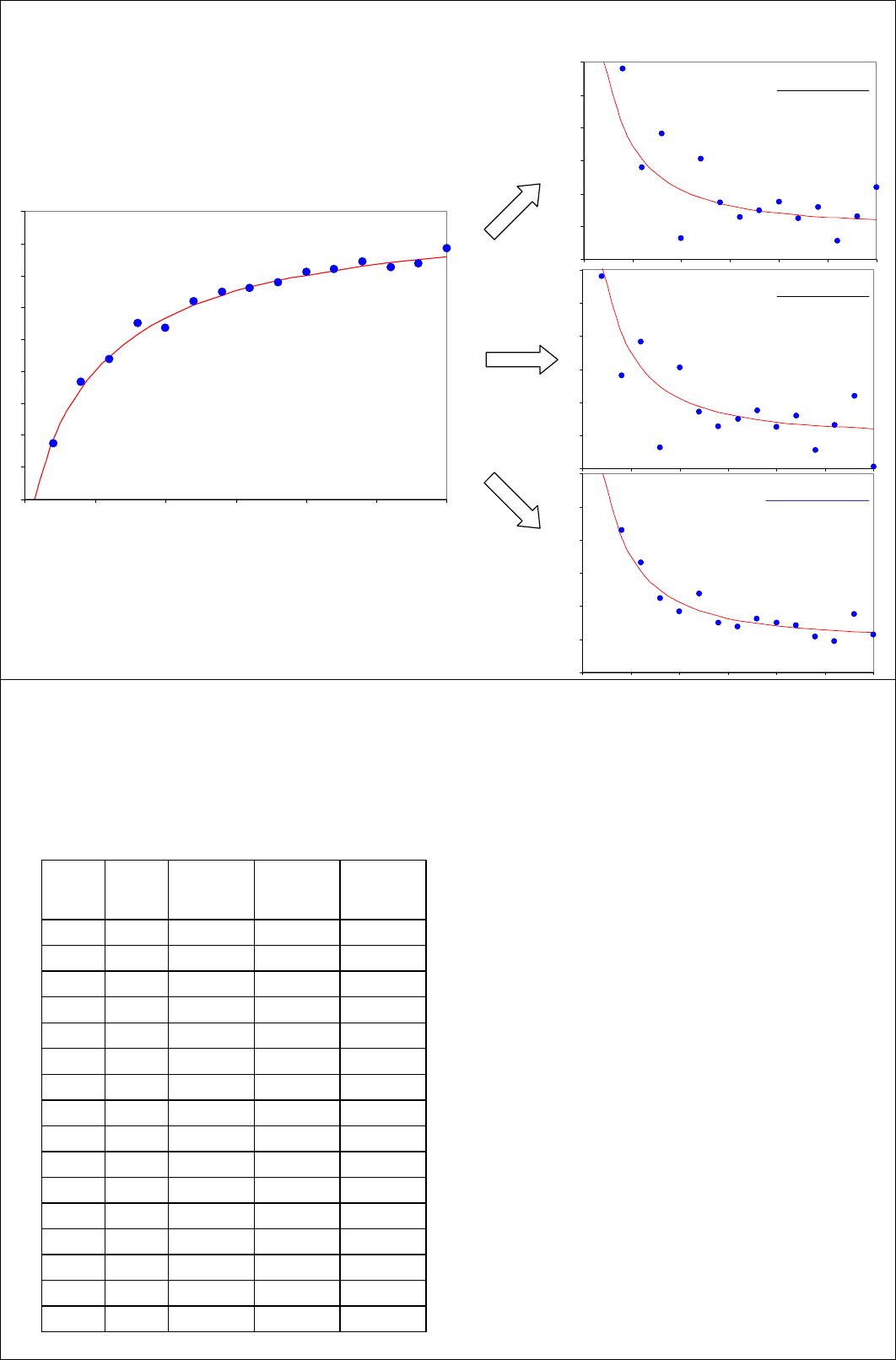
Процесс дифференцирования данных
усиливает шум, присущий данным
Непосредственное дифференцирование
может дать очень зашумленную
производную, поэтому необходимо
сглаживать данные

Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
92
5.3 Вычисление производной
Многоточечная регрессия Скользящее окошко
δδ
δδ
l
1
l
2
m
1
m
2
12 21
i
12
ml ml
m
ll
+
=
+
• Существует множество алгоритмов сглаживания данных
• В основе этих алгоритмов лежит понятие интервала дифференцирования δ
• Для того, чтобы найти значение производной в точке t
i
, рассматривают
интервал [ln t
i
- δ; ln t
i
+ δ ]
• К наиболее распространенным алгоритмам сглаживания данных относятся:
– Многоточечная регрессия
Через точки, попавшие в интервал [ln t
i
- δ; ln t
i
+ δ ], проводится
регрессионная прямая. Наклон это прямой линии есть значение
производной в точке
t
i
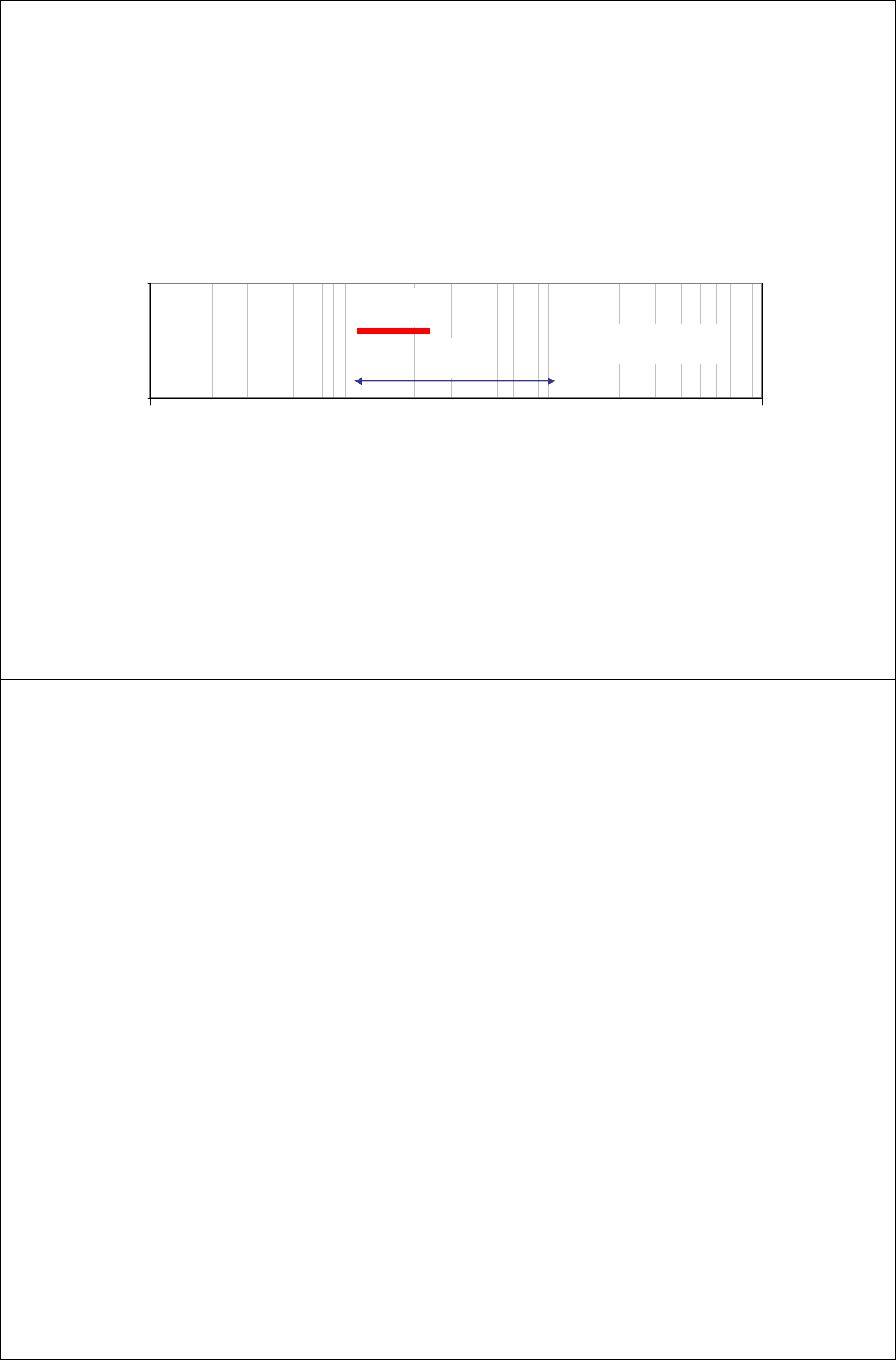
– Скользящее окошко
Через точки (ln t
i
– δ) и (ln t
i
) проводят прямую линию, определяют ее
наклон m
1
. Через точки (ln t
i
)и (ln t
i
+ δ) проводят прямую линию,
определяют ее наклон m
2
. Производная в точке t
i
есть среднее
арифметическое наклонов m
1
и m
2
. В общем случае, если точки
расположены неравномерно по времени, прямые строятся через точку t
i
и
самые дальние от нее точки, попадающие в интервал [ln t
i
- δ; ln t
i
+ δ ]. В
данном случае производная равна средневзвешенному наклонов m
1
и m
2
(обозначения см. на рисунке):
5.3 Вычисление производной
12 21
i
12
ml ml
m
ll
+
=
+
Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
93
5.3 Вычисление производной
2δ< 0.35 длины логарифмического цикла
0.01 0.1 1 10
b
2δ
2δ<0.35b
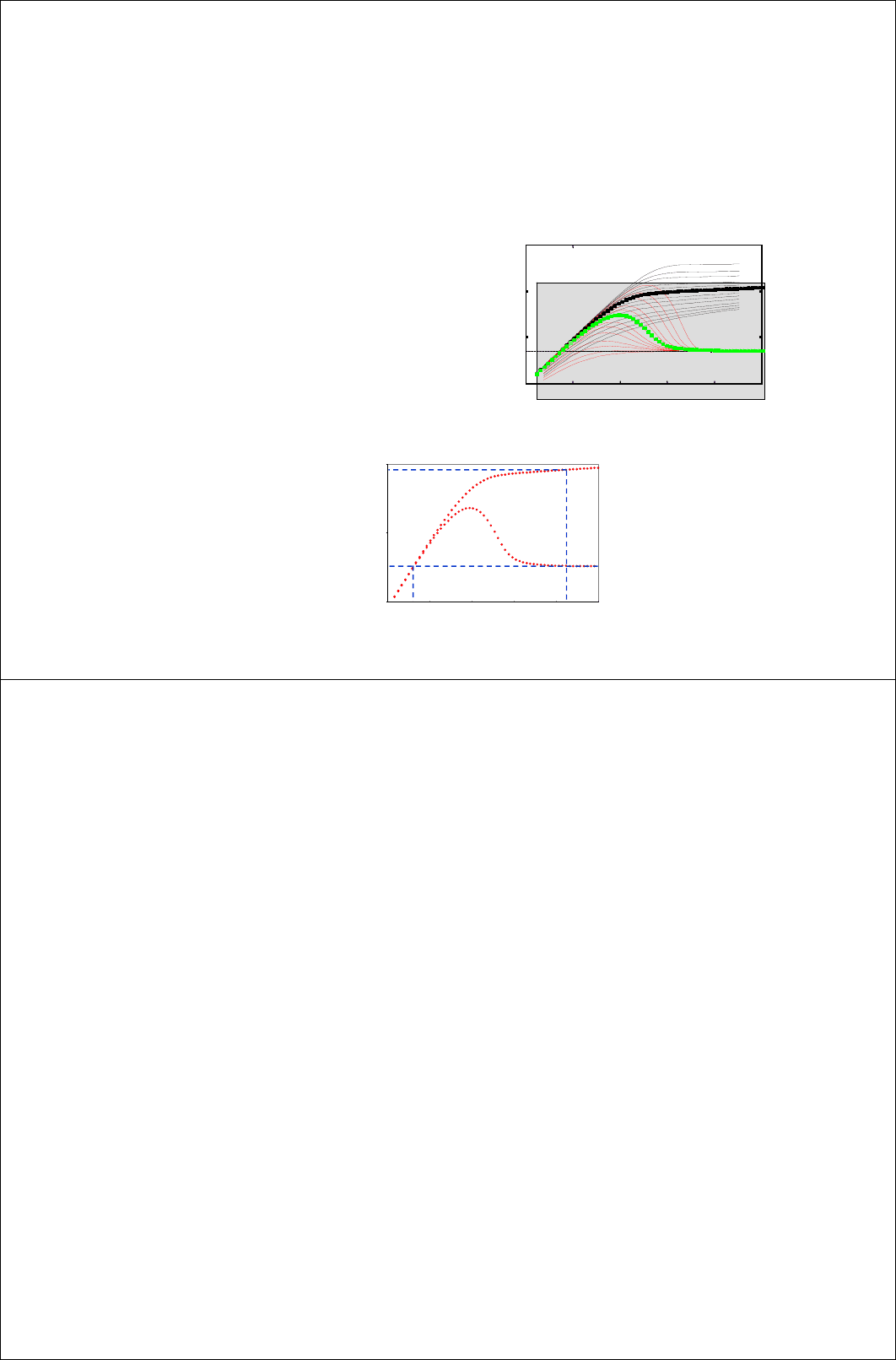
• При сглаживании данных необходимо всегда помнить, что «чрезмерное»
сглаживание может привести к потере информации
• Существует эмпирическое правило выбора длины интервала
дифференцирования δ: 2δдолжно быть не больше 0.35 длины
логарифмического цикла
• Это правило основано на наблюдении того факта, что все переходные
режимы течения длятся не меньше, чем 2/3 длины логарифмического цикла
• Использование максимального значения интервала сглаживания допустимо
лишь в случае чрезвычайно зашумленных данных
5.3 Вычисление производной
Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
94
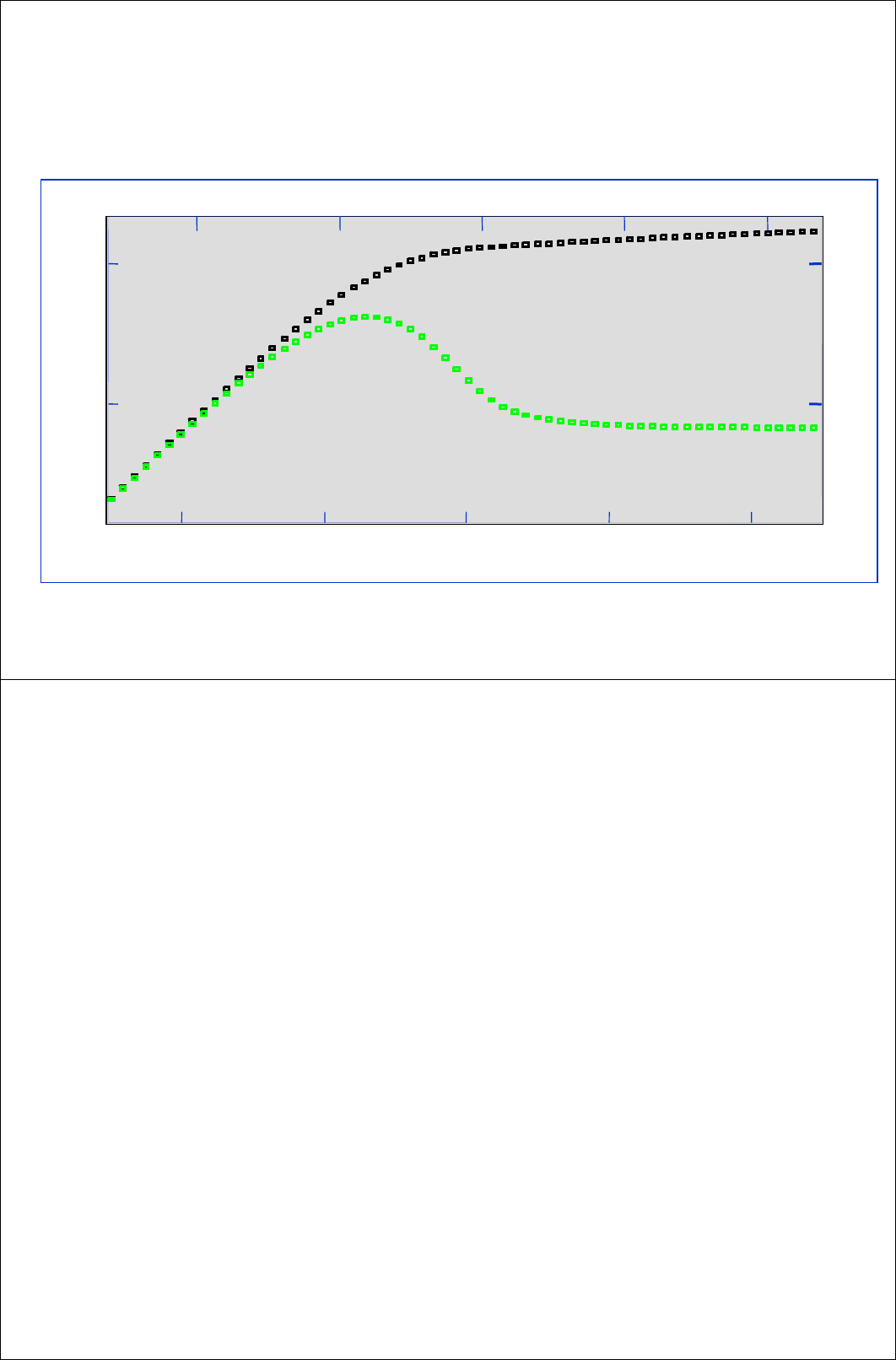
Метод с использованием
типовых кривых
Прямой метод
5.4 Анализ данных с использованием
производной
• Производная давления по логарифму времени позволяет анализировать
данные двумя методами:
– С использованием типовых кривых
– Прямым методом, используя свойства производной
5.4 Анализ данных с использованием
производной
Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
95
10
0.01 0.1 1 10 100
∆P
P’
t
100
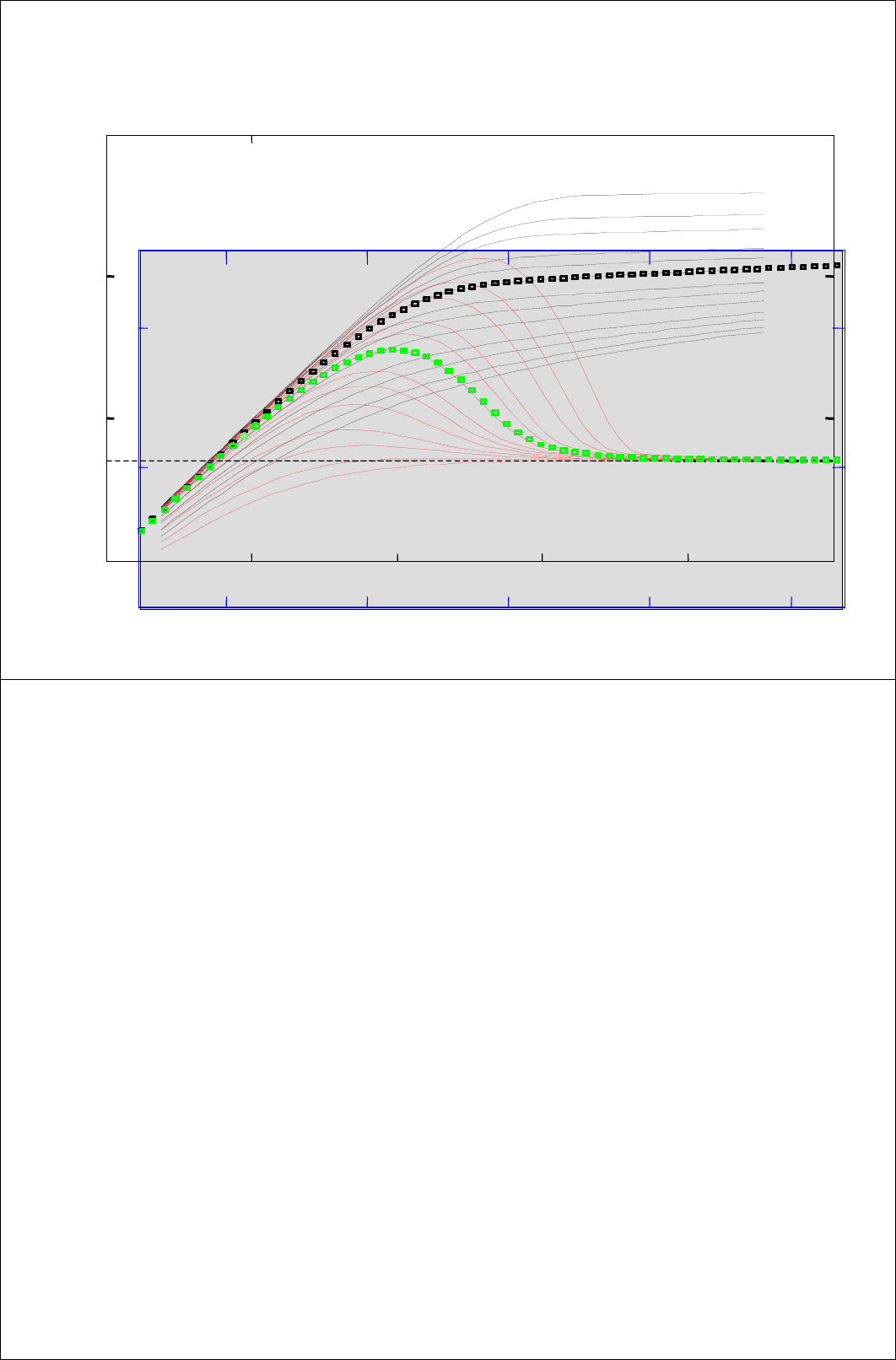
5.5 Анализ c помощью типовых кривых
• Метод анализа с помощью типовых кривых с использованием
логарифмической производной давления подобен процедуре, описанной в
главе 4:
– Нанести данные по давлению и производную на график в
билогарифмическом масштабе. Обязательно масштаб осей должен
совпадать с масштабом осей типовых кривых!
5.5 Анализ c помощью типовых кривых
Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
96
0.1
0.1
1
10
100
1 10 100 10
3
10
4
P
D
P
D
’
t
D
/C
D
0.5
∆P
P’
t
100
10
0.01 0.1 1 10 100
1
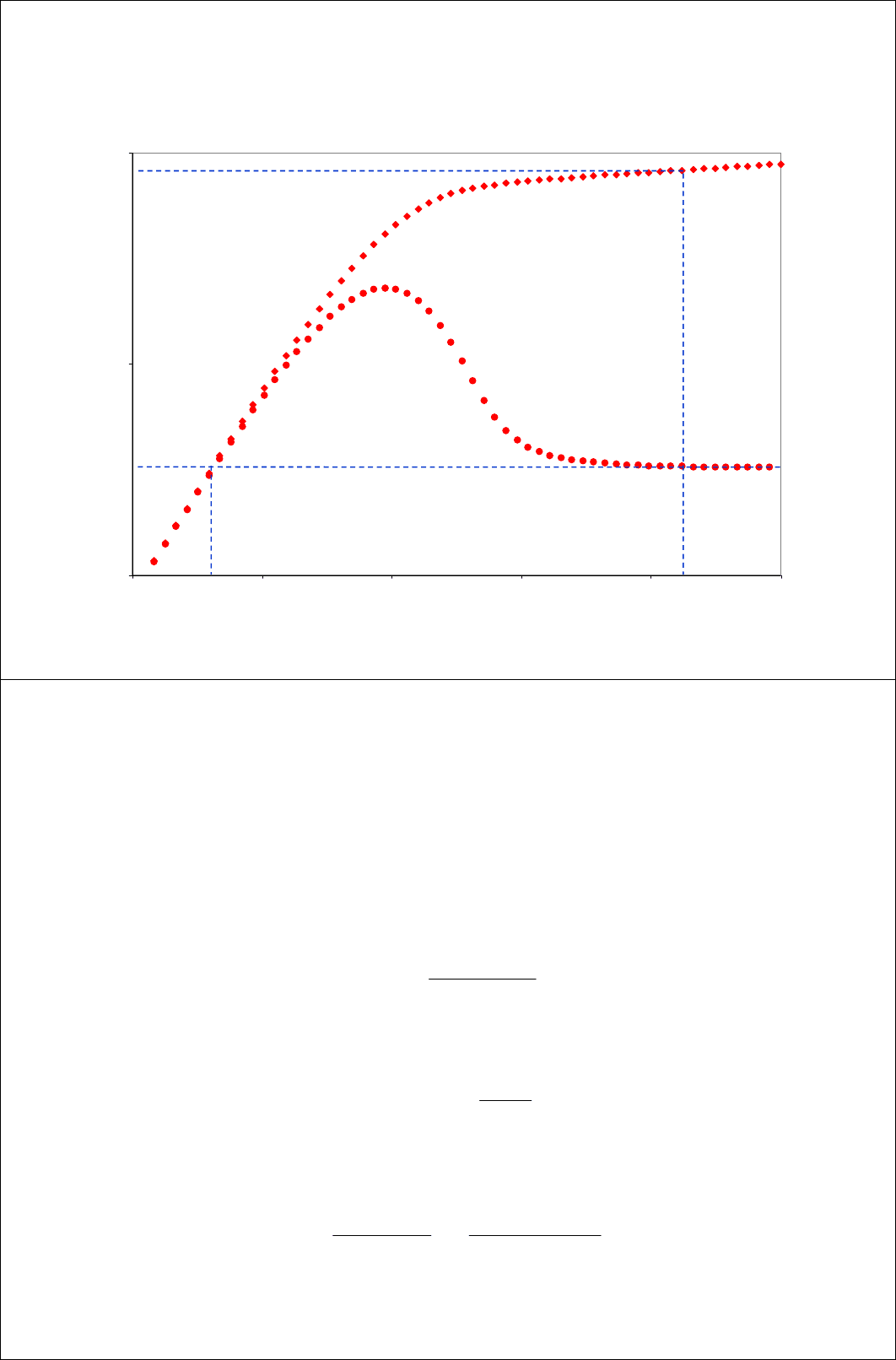
5.5 Анализ c помощью типовых кривых
• Совместить данные с наиболее подходящей типовой кривой
– Основное преимущество использования типовых кривых с
производной – существенная помощь в выборе типовой кривой.
Процесс совмещения реальных данных с определенной типовой кривой
осуществляется в два этапа:
~ Совмещение по оси давления: точки производной, лежащие на
горизонтальной линии совмещаются с горизонтальным участком
типовых кривых
~ Совмещение по оси времени: точки производной, лежащие на
линии наклона 1, соответствующей ВСС, совмещаются с линией
наклона 1 типовой кривой
• Выбор определенной пары кривых соответствует фиксированному
значению параметра C
D
exp(2S)
• Выбрать любую точку М на графике (необязательно на кривой) иснятьее
координаты с обоих графиков: ([t]
M
, [∆P]
M
) и ([t
D
/C
D
]
M
, [P
D
]
M
)
• Формулы для анализа аналогичны формулам, описанным в главе 4
5.5 Анализ c помощью типовых кривых
Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
97
5.6 Прямой анализ с использованием
производной
t
скин
∆P
скин
t
стаб
∆P
стаб
• Анализировать данные можно без типовых кривых, используя свойства
производной:
– С момента достижения радиального притока производная давления
стабилизируется, а безразмерное значение давления равно 0,5. Отсюда
– Во время периода ВСС давление линейно зависит от времени:
– Значение скин-фактора можно найти из соотношения:
при условии, что в момент t
скин
скважина вышла на радиальный приток
стаб
kh
0.5 P
18.41qB
=∆
µ
стаб стаб
s
qB
P
t
24C
∆=
скин
скин
2
tw
0.00036kt
9.205qB
Pln0.812S
kh c r
µ
∆= ++
ϕµ
5.6 Прямой анализ с использованием
производной

Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
98
стаб
s
стаб
t
qB
C
24 P
=⋅
∆
стаб
0.5
kh 18.41qB
P
=µ⋅
∆
скин скин
2
стаб tw
P 0.00036kt
1
Sln 0.81
2P cr
∆
=− −
∆ϕµ
5.6 Прямой анализ с использованием
производной
• Используя эти соотношения, получаем оценки параметров по формулам:
стаб
0.5
kh 18.41qB
P
=µ⋅
∆
стаб
s
стаб
t
qB
C
24 P
=⋅
∆
скин скин
2
стаб tw
P 0.00036kt
1
Sln 0.81
2P cr
∆
=− −
∆ϕµ
5.6 Прямой анализ с использованием
производной

Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
99
Упражнение 1
Было проведено исследование (все то же) по КВД. Данные
давления представлены на рисунке
Задание: Проанализируйте данные методами типовых кривых
и прямым методом с использованием производной давления.
Определите коэффициент ВСС, проницаемость и скин-фактор
240
245
250
255
260
265
270
-15 0 15 30 45 60 75
время, часы
Давление, атм
-20
0
20
40
60
80
100
120
Дебит, м
3
/сут
давление
дебит
Упражнение 1
Исходные данные
атм245.4p(∆t = 0)
м
3
/сут110qДебит
час48t
p
Время работы скважины
1/атм2.20E-04c
t
Общая сжимаемость
спз1µВязкость нефти
м
3
/м
3
1BОбъемный коэффициент нефти
м0.08r
w
Радиус скважины
м80hПродуктивная толщина
0.2φПористость

Центр Профессиональной Переподготовки Специалистов Нефтегазового Дела
100
1. Какая производная используется в ГДИС для диагностики модели
– первая,
– вторая,
– логарифмическая?
2. Как выглядит производная давления для радиального режима течения
на графике в билогарифмических координатах?
3. Как выглядит производная в период доминирования ВСС на графике в
билогарифмических координатах?
4. Почему процесс совмещения реальных данных с типовой кривой
упрощается при наличии производной давления?
Контрольные вопросы к главе 5
