Макаров Е.Г. Сопротивление материалов
Подождите немного. Документ загружается.

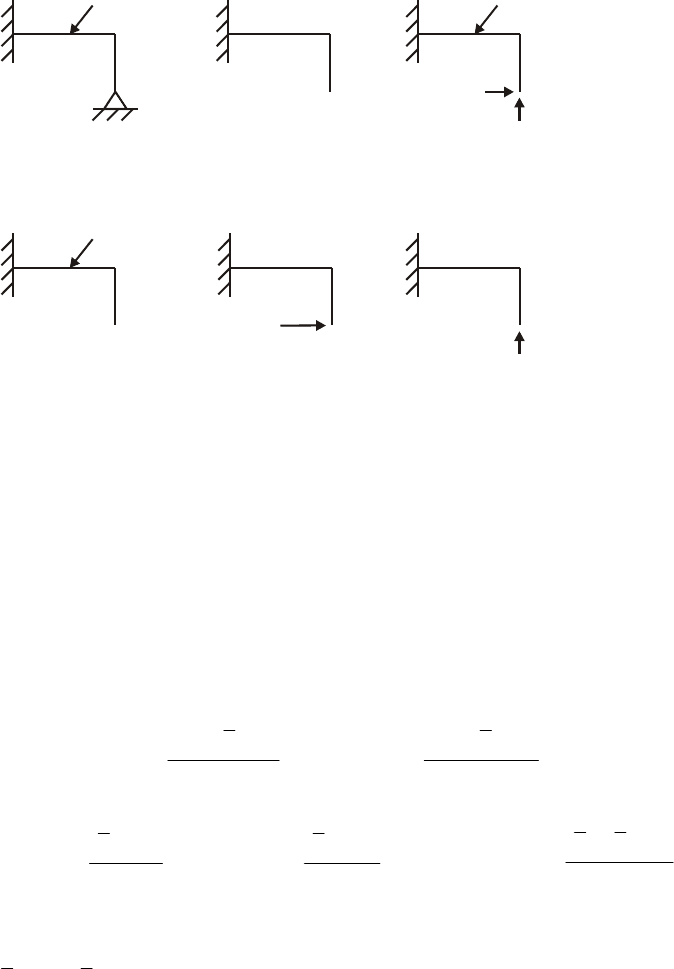
11.2.3. Канонические уравнения метода сил
СУЩНОСТЬ МЕТОДА СИЛ
Заданную статически неопределимую систему заменить статически определимой,
ей эквивалентной, путем отбрасывания лишних связей и замены их неизвестными
силами. Величину этих сил определяем из условий эквивалентности.
Две системы считаются эквивалентными, если напряжения, деформации и
перемешения в них одинаковы.
Если системы упругие, для их эквивалентности достаточно, чтобы перемещения в
них были одинаковы.
Реализацию описанной идеи рассмотрим на примере два раза статически
неопределимой системы (рис. 11.6, а). Отбросим две связи (любые), система станет
статически определимой. Назовем ее основной системой.
Из одной заданной системы можно получить несколько основных (статически
определимых систем) путем отбрасывания разных связей. Выбранная основная
система (рис. 11.6, б) обеспечивает более простое решение.
F
A
a)
заданная
система
F
x
2
в)
эквивалентная
система
x
1
F
г)
грузовая
с
и
с
т
е
м
а
д)
единичные системы
x=1
1
x=
1
2
е)
б
)
основная
система
Рис. 11.6. Расчетные схемы, используемые в методе сил
Нагрузим основную систему всеми внешними силами, действие отброшенных связей
заменим неизвестными силами
1
X
и
2
X
, получим эквивалентную систему
(рис. 11.6, в).
На опоре
А линейные перемещения равны нулю. Используем равенство нулю этих
перемещений в качестве условий эквивалентности
.верт
.гор
0
0
A
A
Δ=
Δ=
Согласно принципу независимости действия сил и закона Гука (11.2)
А.гор 12
А.верт 12 22 2
0
0
F
F
XX
XX
δ
δ
δδ
11 12 1
12
Δ= + +Δ=
Δ= + +Δ=
(11.3),
где
3
,1,
1
k
Fk k
F
k
L
M
Mdx
EJ
1
=
Δ=
∑
∫
и
3
,2,
2
1
k
Fk k
F
k
L
M
Mdx
EJ
=
Δ=
∑
∫
— перемещения по
направлениям 1 и 2 от внешних сил,
2
3
1,
11
1
k
k
k
L
M
dx
E
J
δ
=
=
∑
∫
2
3
2,
22
1
k
k
k
L
M
dx
E
J
δ
=
=
∑
∫
3
1, 2,
12
1
k
kk
k
L
M
Mdx
EJ
δδ
21
=
==
∑
∫
—
коэффициенты податливости, учитывающие только изгиб элементов рамы.
k — номер участка,
,
F
k
M
— изгибающий момент от внешних сил на участке k ,
1,k
M и
2,k
M — изгибающие моменты от единичных сил
1
1X
=
и на
участке
k .
2
1X =
Для определения указанных изгибающих моментов на рис. 11.6 нарисованы еще три
системы: грузовая (рис. 11.6, г) и две единичные от силы
1
1X
=
(рис. 11.6, д) и от
силы (рис. 11.6, е).
2
1X =
Решая систему уравнений (11.3) определяем неизвестные силы
1
X
и
2
X
.
Статическая неопределимость раскрыта.
Далее для статически определимой эквивалентной системы можно определить
напряжения и перемещения, как было описано ранее.
121

Для раз статически неопределимой системы надо записать условий
эквивалентности
n n
12
12 22 2
12
... 0
... 0
......................................................
... 0
nn
nn
nn nnn
XX X
XX X
XX X
δδ δ
δδ δ
δδ δ
11 12 1
12
12
+++=
⎧
⎪
+++=
⎪
⎨
⎪
⎪
+++=
⎩
(11.4).
Это
система канонических уравнений метода сил
.
Она не изменяется для любой
задачи.
В общем виде систему уравнений (11.4) можно записать как перемещение по
направлению
i
,,
1
0
=
Δ= +Δ =
∑
n
ijijiF
j
X
δ
(11.5),
где
n — степень статической неопределимости (число неизвестных сил
i
X
).
В выражениях (11.4) и (11.5) все коэффициенты представляют собой перемещения,
которые определяются с помощью интеграла Мора.
В общем случае в интеграл Мора можно включать слагаемые, учитывающие
продольные усилия, изгибающие моменты и крутящие моменты. Тогда перемещение
от внешних сил по направлению
i
,, , , к,, к,,
,
11 1
к
== =
Δ= + +
∑∑ ∑
∫∫ ∫
kk k
mm m
Fk ik Fk ik Fk ik
iF
kk k
kk
LL L
N N dS M M dS M M dS
EA EJ GJ
(11.6),
коэффициенты податливости
,, , , к,, к,,
,
11 1
к
== =
=+ +
∑∑ ∑
∫∫ ∫
kk k
mm m
ik jk ik jk ik jk
ij
kk k
kk
LL L
N
NdS MMdS M M dS
EA EJ GJ
δ
(11.7).
В этих выражениях — число участков, — номер участка.
m k
На практике, как правило, пренебрегают влиянием продольных усилий, если есть
изгибающие или крутящие моменты. Численные расчеты в приведенных в
электронной книге примерах показали, что слагаемые перемещений от продольных
усилий примерно в тысячу раз меньше слагаемых от моментов (изгибающих или
крутящих).
Определив все необходимые коэффициенты, решают систему уравнений (11.4) и
находят все неизвестные силы
i
X
.
После нахождения неизвестных сил становится возможным работать с эквивалентной
системой, для которой теперь можно найти все внутренние усилия (моменты
изгибающие и крутящие).
На основании принципа независимости действия сил момент (изгибающий или
крутящий) для эквивалентной системы равен сумме моментов от каждой силы в
отдельности или
экв
1
n
F
ii
i
M
MX
=
=+
∑
M
(11.8).
Для эквивалентной статически определимой системы можно найти напряжения и
перемещения, которые являются такими же, как в заданной системе.
Зная моменты в эквивалентной системе относительно осей
,,
x
yz, надо выбрать
опасное сечение, где действуют максимальные эквивалентные напряжения по
третьей или четвертой гипотезам прочности, как показано в предыдущей главе при
сложном сопротивлении. Следует заметить, что иногда бывает необходимо
рассмотреть два и более опасных сечения.
Если требуется найти перемещение какой-либо точки заданной системы, то это
перемещение определяется для эквивалентной системы с помощью интеграла Мора.
При этом в качестве моментов от внешних сил используются выражения для
моментов в эквивалентной системе, найденные ранее.
11.2.4. Учет монтажных и температурных напряжений
При необходимости учета температурных или монтажных напряжений
соответствующие слагаемые добавляются в канонические уравнения метода сил (11.4
и 11.5).
,, ,i,монт
1
0
=
Δ = +Δ +Δ +Δ =
∑
n
ijijiFit
j
X
δ
.
здесь и — перемещения точки приложения силы
,it
Δ
,монтi
Δ
i
X
в направлении этой
силы соответственно от действия температуры и от монтажной погрешности при
сборке конструкции, — степень статической неопределимости.
n
122
,
1
m
it k
k
Lt
α
=
Δ= Δ
∑
, где
α
— коэффициент температурного расширения материала
стержней, — приращение температуры,
tΔ
k
L
— расстояние от неподвижной точки
до точки приложения силы
i
X
в направлении этой силы,
,монтi
Δ
— монтажная
погрешность при сборке (задается). Определение температурного смещения точки
приложения силы Х
I
должно быть тщательно продумано. Примеры учета
воздействия изменения температуры и монтажных погрешностей приведены в
электронной книге в разделе
Для главы 11.
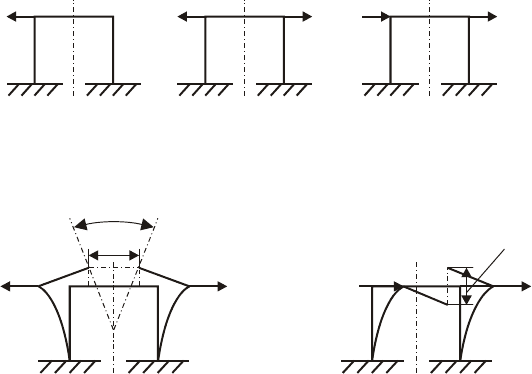
11.2.5. Учет симметрии в методе сил
Степень статической неопределимости системы уменьшается в случае симметрии
системы. Если система геометрически симметрична, но нет симметрии нагрузок
(рис. 11.7, а), то в этом случае степень статической неопределимости не меняется.
Система на рисунке 3 раза статически неопределима.
При наличии геометрической симметрии и симметрии нагружения различают
системы
прямосимметричные и кососимметричные.
Если при сложении половинок системы по геометрической оси симметрии,
направления внешних сил совпадают, то такая система называется
прямосимметричной (рис. 11.7, б)
,
если направления внешних сил противоположны,
то система называется
кососимметричной (рис.11.7, в).
F
a)
несиммет
р
ичная
F
б
)
п
р
ямосиммет
р
ичная
F F
в)
кососиммет
р
ичная
F
Рис. 11.7. Несимметричная, прямосимметричная и кососимметричная системы
a)
F
прямосимметричная
система
F
A
1
A
2
A
кососимметричная
система
б)
F
F
A
1
A
2
A
12
A
A
θ
12
.гор
A
A
Δ
12
.верт
A
A
Δ
Рис. 11.8. Учет симметрии в методе сил
Прямосимметричную систему разрежем по оси симметрии и посмотрим на
перемещения половинок системы (рис. 11.8, а). Точка
А, лежащая на оси симметрии
при этом превращается в две точки
А1
и А2 соответственно на левой и правой
половинках системы.
По вертикали точки
А1 и А2 остаются на одном уровне
2
верт
0
A
1
Α
Δ
=
, следовательно
сила, стягивающая вместе две половинки в этом случае равна нулю
0Q
=
.
По горизонтали точки А
1
и А
2
разошлись, следовательно надо приложить
горизонтальную силу, чтобы свести две половинки вместе
0N
≠
.
Поперечные сечения в точках А
1
и А
2
развернулись друг относительно друга на
некоторый угол
12
0
AA
θ
≠
. Чтобы этот угол был равен нулю, надо приложить пару
сил .
0M ≠
Рассматриваемая прямосимметричная система стала два раза статически
неопределимой. В качестве эквивалентной системы можно взять одну половину
системы и в месте разреза приложить неизвестные силы
1
X
N
=
и
2
X
M= .
Кососимметричную систему разрежем по оси симметрии и посмотрим на
перемещения половинок системы (рис. 11.8, б).
По вертикали точки
А1 и А2 расходятся
2
верт
0
A
1
Α
Δ
≠
, следовательно необходима
сила, стягивающая вместе две половинки
0Q
≠
.
По горизонтали точки
А1 и А2 находятся на одном уровне, следовательно
горизонтальная сила, сводящая две половинки вместе равна нулю
0N
=
.
Поперечные сечения в точках А1 и А2 развернулись на один и тот же угол.
Следовательно взаимный угол поворота сечений
12
0
AA
θ
=
и пара сил, сводящая две
половинки вместе равна нулю
0M
=
. Рассматриваемая кососимметричная система
123
стала один раз статически неопределимой. В качестве эквивалентной системы можно
взять одну половину системы и в месте разреза приложить неизвестную силу
1
X
Q= .
ПРАВИЛО
При разрезании системы по оси симметрии:
в прямосимметричной системе обращаются в нуль кососимметричные усилия
(поперечная сила
Q и крутящий момент
к
M
);
в кососимметричной системе обращаются в нуль прямосимметричные усилия
(продольное усилие
N
и изгибающий момент
M
).
11.2.6. Проверка правильности решения системы
Если подставить найденные значения сил в канонические уравнения, то ответ должен
быть равен нулю, то есть перемещения в местах раскрепления системы должны быть
равны нулю.
Проверку желательно делать при другом раскреплении системы (для другой
эквивалентной системы). Если определять перемещения в местах раскрепления
первоначальной эквивалентной системы, то при этом проверяется лишь правильность
решения системы канонических уравнений.
При выборе для проверки другой эквивалентной системы внутренние усилия в ней
остаются такими же, как в первоначально взятой эквивалентной системе, а вот
усилия от единичной силы становятся другими. Хотя единичная сила теперь
прикладывается в другой точке раскрепления, текущие координаты
i
x
берутся
также, как при раскрытии статической неопределимости. Это необходимо, чтобы
использовать уже готовые выражения для эквивалентных моментов.
11.2.7. Порядок решения статически неопределимой задачи
методом сил
Изобразить основную статически определимую систему, полученную из
заданной путем отбрасывания лишних связей.
Изобразить систему, эквивалентную заданной, нагруженную всеми внешними
силами и реакциями отброшенных связей.
Изобразить грузовое и единичное состояние основной системы. Количество
единичных состояний равно степени статической неопределимости заданной
системы.
Для каждого участка грузового и всех единичных состояний основной системы
указать текущую координату для произвольного сечения (
x
— для
прямолинейных и
ϕ — для криволинейных участков).
Найти опорные реакции отдельно для грузового состояния и всех единичных
состояний. Если основная система защемлена одним концом, реакции в заделке
можно не определять.
Для произвольного сечения на каждом участке основной системы записать
выражения для внутренних усилий (как правило, только для изгибающих и
крутящих моментов) для грузового и всех единичных состояний.
Записать систему канонических уравнений метода сил (11.4) для эквивалентной
системы. Определить коэффициенты податливости (11.7) и перемещения от
внешних сил (11.6), входящие в канонические уравнения. Решив систему
канонических уравнений, определить все неизвестные силы.
Последующие действия производятся с эквивалентной системой.
Найти внутренние усилия (11.8).
Определить необходимые перемещения. При этом в качестве усилий от
внешних сил берутся усилия в эквивалентной системе. Единичное состояние
основной системы соответствует искомому перемещению.
Произвести расчет на прочность с использованием условия прочности.
11.3. Определение перемещений систем из
нескольких элементов
Энергетический метод позволяет определить перемещения любых упругих систем.
Для систем, собранных из большого количества элементов сохраняется тот же
порядок расчета, но общий объем расчетов многократно увеличивается.
124
Порядок расчета перемещений обычный для энергетического метода.
Нарисовать грузовую и единичную системы. Единичную систему нагрузить
единичной силой в точке, где ищем перемещение в направлении
перемещения.
Определить внутренние усилия в элементах системы для грузового и
единичного состояния.
Определить перемещение с помощью интеграла Мора.
Для определения внутренних усилий в элементах системы ее надо разобрать и
рассмотреть силы, действующие на каждый элемент в отдельности.
В качестве примера рассмотрим перемещение плоской системы. Рассмотрим систему,
состоящую из балок, связанных между собой стержнями и пружинами.
Вклад в общее перемещение изогнутых балок определяется по формуле
F
L
MM
dx
EJ
Δ=
∑
∫
.
Вклад в перемещение сжатых или растянутых стержней
F
L
NN
dx
EA
Δ=
∑
∫
.
В стержнях, соединяющих балки, продольное усилие постоянное
N
Const= и
может быть вынесено из под знака интеграла
ст
FF
N
NN
L
EA K
Ν
Δ= =
∑∑
,
где
ст
E
A
K
L
=
— жесткость стержня.
По аналогии для пружин, нагруженных осевой нагрузкой
пр
F
N
K
Ν
Δ=
. Жесткость пружины выбирается по справочникам при подборе
пружины или рассчитывается.
пр
K
ПРИМЕЧАНИЕ
В роли пружины может выступать "черный ящик", сложная конструкция, жесткость
которой трудно рассчитать, но легко определить опытным путем. Достаточно
приложить известную нагрузку, чаще всего вес груза, и измерить перемещение по
направлению действия нагрузки.
Формула для определения перемещения сложной системы принимает вид
ст пр
FF F
L
NN N MM
dx
KK EJ
Ν
Δ= + +
∑∑
∫
(11.9).
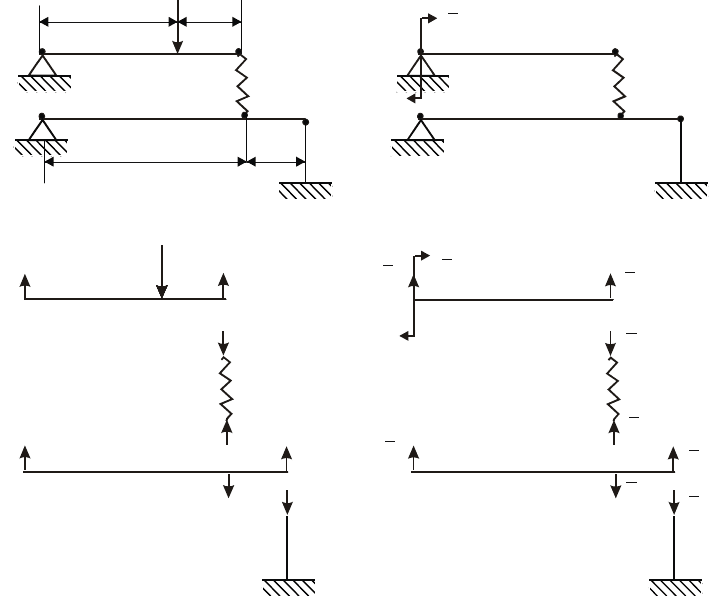
Определим перемещение системы, состоящей из двух балок, связанных пружиной и
стержнем (рис. 11.9, а). Задана геометрия системы (длины участков, форма и размеры
поперечных сечений, для пружины задана ее жесткость ), материал, нагрузка F.
Требуется определить угол поворота сечения балки на опоре D.
пр
K
125
а)
б)
в) г)
L
4
L
3
L
2
L
1
F
D
B
1
M
=
D
В
D
В
F
D
R
B
R
1
N
1
N
1
N
1
N
2
N
2
N
D
В
1
M
=
D
R
1
N
1
N
1
N
1
N
2
N
2
N
B
R
Рис. 11.9. Расчетные схемы для определения перемещения системы из нескольких элементов
Заданная система является грузовой (рис. 11.9, а). Для определения угла поворота на
опоре D нарисована единичная система (рис. 11.9, б).
Для определения внутренних усилий разберем на отдельные элементы каждую из
нарисованных систем (грузовую и единичную) и из уравнений равновесия каждого
элемента определим внутренние усилия. Деталировка грузовой и единичной системы
показана на рис. 11.9, в и г.
Из условия равновесия балок (верхней и нижней) найдем усилия N
1
и N
2
,
действующие на пружину и стержень, а также опорные реакции. Далее запишем
изгибающие моменты на всех четырех участках грузовой и единичной систем.
Подставив выражения для найденных внутренних усилий в формулу (11.9), найдем
угол поворота на опоре D. Подробное решение этой задачи приведено в электронной
книге.
Таким же образом, разбивая систему на элементы, можно решить и статически
неопределимую систему, но объем расчетов при этом значительно возрастет.
126
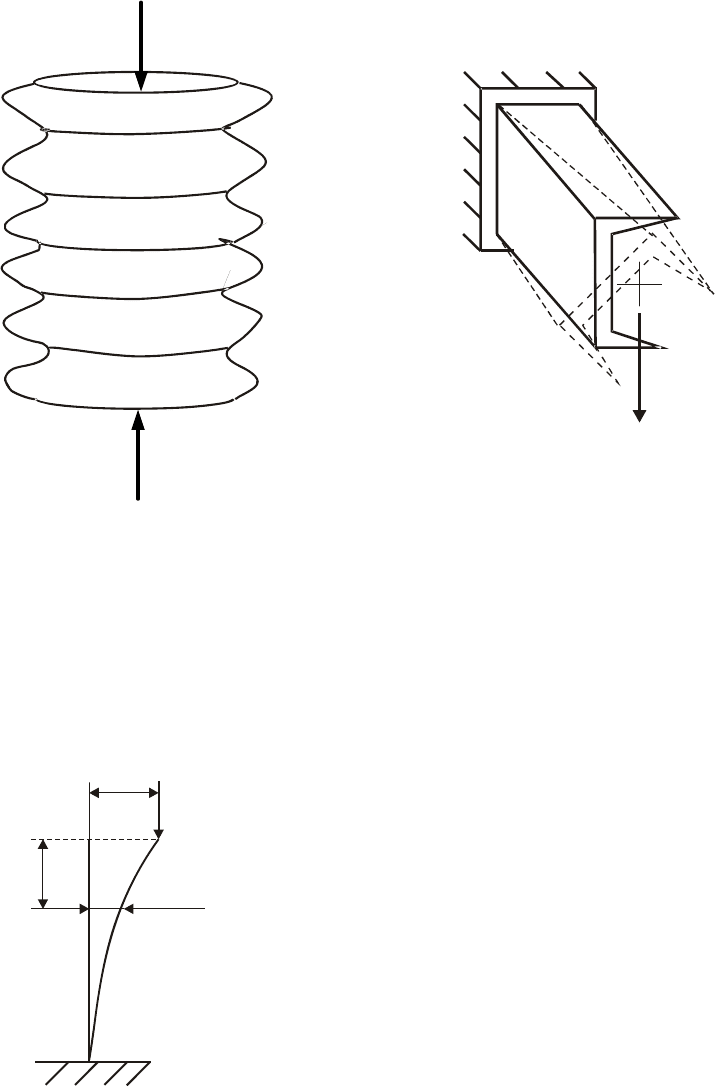
Глава 12. Устойчивость сжатых стержней
Под механической устойчивостью будем понимать способность тела
сохранять заданную форму равновесия.
Потеря механической устойчивости — резкое изменение вида
деформации. Приведем несколько примеров потери устойчивости.
На рисунке 12.1,а показана потеря устойчивости цилиндрической
оболочки при сжатии. В момент потери устойчивости сжатие оболочки
сменяется ее изгибом. Правда на практике чаще имеет место чашечная
потеря устойчивости оболочек. Вспомните, как выглядит банка из-под
пива, на которую наступили ногой.
На рисунке 12.1,б показан изгиб швеллера. При достижении
критического значения изгибающей силы балка скручивается.
На рисунке 12.2 показано сжатие стержня. При некотором
критическом значении сжимающей силы происходит изгиб стержня.
F
)
a
)
б
F
F
Рис 12.1. Примеры потери устойчивости конструкций
Критической называется минимальная нагрузка, при которой система
теряет устойчивость.
Далее в этой главе рассмотрим только устойчивость сжатых стержней.
Нагрузим стержень сжимающей силой (рис. 12.2) меньше критической
кр
F
F< . Выведем стержень из состояния равновесия (подтолкнем в бок
рукой). Уберем руку, стержень возвратится в состояние равновесия
(изгиб исчезнет).
Рис 12.2. Потеря устойчивости сжатого стержня
При изгибе стержня возникает изгибающий
момент
внеш 0
()
M
Fu u
=
− . Ему
противодействует момент внутренних сил
упр
A
M
ydA
σ
=
⋅⋅
∫
.
Если
изг упр
MM
=
, то стержень находится в
равновесии.
Если , произойдет потеря
устойчивости.
изг упр
MM>
x
u
0
u
F
Если , выведенный из равновесия стержень возвращается в
исходное прямолинейное состояние.
изг упр
MM<
127

Поставим задачу определить критическую силу, при которой стержень
теряет устойчивость.
12.1. Определение критической силы. Формула
Эйлера
Рассмотрим стержень на двух шарнирных опорах, нагруженный
сжимающей силой (рис. 12.3). При увеличении нагрузки в какой-то
момент стержень теряет устойчивость и изгибается в направлении
наименьшей жесткости
min
J
.
u
x
L
F
кр
Рис. 12.3. Схема Эйлера потери устойчивости сжатого стержня
В разделе 7.1 получено выражение, связывающее изгибающий момент
с кривизной балки,
min
1
=
M
EJ
ρ
. Там же приведено выражения для кривизны стержня,
взятое из аналитическое геометрии
()
(
)
3
2
2
1
1
′
′
=
′
+
u
u
ρ
.
Приравнивая два выражения для кривизны и пренебрегая первой
производной от прогиба (углом поворота) по сравнению с единицей,
получаем уравнение упругой линии балки (7.13)
min
E
Ju M
′′
= .
При
кр
F
F= изгибающий момент в произвольном сечении стержня
крz
M
Fu=− .
Знак минус в выражении изгибающего момента поставлен для
согласования знаков прогиба и его второй производной. На рис. 12.3
прогиб балки положительный, а вторая производная отрицательная,
так как функция имеет максимум. Если прогиб будет отрицательным,
то функция будет иметь минимум, то есть вторая производная
положительна.
u
Уравнение изогнутой оси стержня принимает вид
min кр
E
Ju M Fu
′′
==−
.
Приведем это уравнение к стандартному виду, разделив его на
min
E
J
кр
min
0
F
uu
EJ
′′
+=.
Введем
кр
min
F
k
EJ
=
(12.1).
тогда уравнение примет стандартный вид
2
0uku
′′
+= (12.2).
Решение уравнения (12.2) ищем в виде
12
() ()uCCoskx CSinkx=+.
Произвольные постоянные интегрирования находим из граничных
условий
При , следовательно 0x =
0
0=u
1
0C
=
.
При
x
L= . Тогда либо 0
L
u =
2
0C
=
, либо ()0Sin kL
=
.
128

2
C не может быть равно нулю, так как в этом случае не может быть
потери устойчивости
. Следовательно ()0Sin kL
=
. Тогда kL n
π
= и
n
k
L
π
= ,
где n — любое целое число. Но не может быть равно нулю по
вышеуказанной причине
. При
n
1n
=
критическая сила минимальна и
реально имеет место
. На практике могут быть реализованы и другие
значения
, об этом будет сказано далее. 1n >
Приравняем ранее принятое значение k (12.1) и только что найденное
кр
min
F
n
k
EJ L
π
==.
Откуда
2
min
кр
2
EJ
F
L
π
2
= n (12.3).
Минимальному значению критической силы
соответствует .
Тогда формула Эйлера для определения критической силы принимает
вид
1n =
min
кр
2
EJ
F
L
π
2
= (12.4).
Рассмотренную схему нагружения стержня будем называть схема
Эйлера
.
Изогнутая ось стержня в схеме Эйлера представляет собой полволны
синусоиды
2
()uCSinkx= . В этом выражении коэффициент не может быть
определен из граничных условий
. Поэтому максимальный прогиб
стержня неопределенный.
2
C
Считается, что при достижении критической силы прогиб стержня
возрастает до бесконечности
, то есть стержень ломается.
В действительности этого не происходит
. Причина в использовании
приближенного выражения связи кривизны и прогиба
. При
использовании точного выражения
()
(
)
3
2
2
1
1
′
′
=
′
+
u
u
ρ
получается
большое
, но конечное значение прогиба.
12.2. Определение критической силы при других
видах закрепления
Формула Эйлера может быть использована для определения
критической силы и при других видах закрепления
.
а)
F
кр
μ=1
L
б)
F
кр
μ=2
LL
пр
=2
в)
F
кр
μ=0,5
LL
пр
=0,5
г)
F
кр
μ=0,7
LL
пр
=0,7
д
)
F
кр
LL
пр
=0,5
μ=0,5
Рис. 12.4. Приведенная длина стержня при различных способах его закрепления
На рис. 12.4 показано несколько различных способов закрепления
сжатого стержня
. Для стержня, защемленного одним концом (рис.
12
.4, б) изогнутая ось стержня в момент потери устойчивости
представляет собой ¼ волны синусоиды
.
Критическую силу для этого (и всех последующих случаев) найдем
путем сравнения изогнутой оси стержня со схемой Эйлера (рис.12.4, а)
.
Формула Эйлера выведена для случая, когда изогнутая ось стержня
представляет собой полволны синусоиды
. В нашем случае ¼ волны.
129
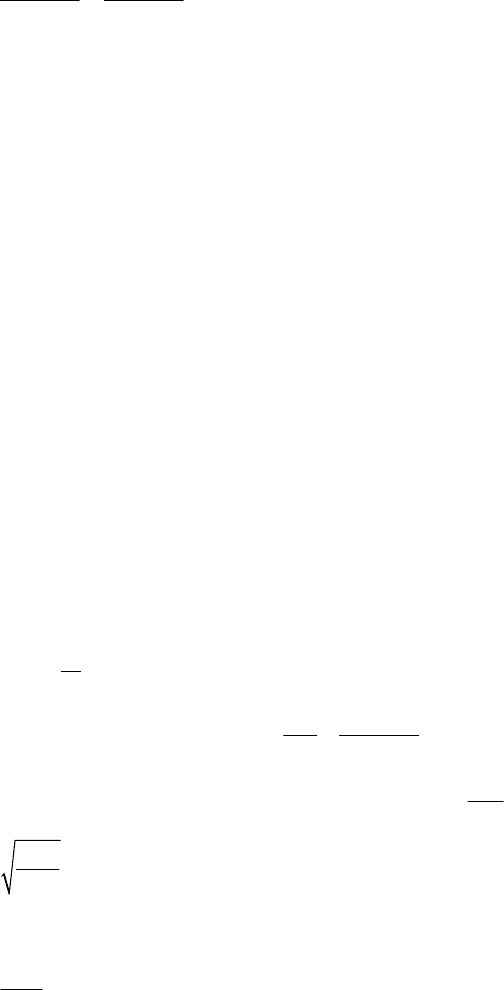
Введем понятие приведенной (к схеме Эйлера) длины стержня.
Достроим изогнутую ось стержня так
, чтобы на ней уложилось
полволны синусоиды
. Длина достроенного стержня и есть приведенная
длина
пр
LL
μ
= .
Определим критическую силу по формуле Эйлера
, используя в
качестве длины стержня его приведенную длину
2
min min
кр
2
пр
()
EJ EJ
F
LL
ππ
μ
2
== (12.5),
где
μ
— коэффициент закрепления стержня, показывающий во
сколько раз надо увеличить длину стержня
, чтобы на нем уложилось
полволны синусоиды
.
На рис
. 12.4, в и 12. 4, г отмечено полволны синусоиды на изогнутой
оси стержня и записан коэффициент закрепления
5
μ
=
0, и 7
μ
=0, .
Кстати коэффициент в выражении (12.3) соответствует числу
полуволн на изогнутой оси стержня
.
n
Если посередине стержня добавить связь
, удерживающую стержень в
исходном положении
, то при потере устойчивости изогнутая ось
стержня будет содержать две полуволны синусоиды
, соответственно
критическая сила возрастет в 4 раза
, в то время как реакция
добавленной связи практически равна нулю
. Схема Эйлера с
добавленной связью посередине показана на рис
. 12. 4, д. Эта схема
соответствует n = 2 в выражении (12.4).
Чтобы изогнутая ось стержня содержала три полуволны синусоиды
надо добавить две связи. Такая схема будет соответствовать n = 3. При
этом критическая сила возрастет в 9 раз.
12.3. Критические напряжения
Поскольку мы рассматриваем устойчивость стержней при сжатии, то
напряжения в момент потери устойчивости определяем по формуле
сжатия
F
A
σ
= .
В критическом состоянии
кр
min
кр
2
A
()
F
EJ
LA
π
σ
μ
2
== .
Введем понятие гибкости стержня. Обозначим
min
L
i
μ
λ
= , где
min
min
J
i
A
=
— минимальный радиус инерции поперечного сечения
стержня, и назовем коэффициент
λ
гибкостью стержня. Тогда
формула критического напряжения примет вид
кр
E
π
σ
λ
2
2
= . (12.6).
Итак, мы имеем две формулы Эйлера: формулу критической силы
(12.5) и формулу критического напряжения (12.6).
Формулой Эйлера можно пользоваться только при упругой
деформации, то есть в том случае, если критическое напряжение
меньше предела пропорциональности материала
кр пц
σ
σ
<
.
В основе вывода формулы Эйлера лежит уравнение упругой линии
стержня. Ограничивает применение формулы также присутствие в ней
модуля Юнга, коэффициента пропорциональности в законе Гука.
Анализируя формулу (12.6), отметим, что с уменьшением гибкости
критическое напряжение возрастает, а гибкость уменьшается с
уменьшением длины стержня. Чем короче стержень, тем больше
критическое напряжение, при котором он теряет устойчивость.
Потерю устойчивости стержней в условиях пластических деформаций
изучали многое ученые. Было предложено много различных формул
130
