Лысак О.Н. (сост.) Кинематика точки и простейшие движения твёрдого тела
Подождите немного. Документ загружается.

Федеральное агентство по образованию
Томский государственный
архитектурно - строительный университет
КИНЕМАТИКА ТОЧКИ
И ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЁРДОГО ТЕЛА
Методические указания по теоретической механике
Составитель О.Н. Лысак
Издание второе, исправленное
Томск 2007

Кинематика точки и простейшие движения твёрдого тела: Ме-
тодические указания /Сост. О.Н. Лысак. Томск: Изд-во Том. гос. ар-
хит.-строит. ун-та, 2007. – 52 с.
Рецензент профессор О.В. Матвиенко
Редактор Г.Г. Семухина
Методические указания составлены для студентов всех форм
обучения. В них содержатся материалы, включающие разделы ки-
нематики точки и простейшие движения твёрдого тела. В указаниях
приведены примеры решения задач, которые могут оказать помощь
при выполнении курсовых работ студентами дневных форм обуче-
ния; дан список рекомендуемой учебной литературы.
Печатается по решению методического семинара кафедры
теоретической механики № 3 от 3 октября 2006 г.
Утверждены и введены в действие проректором по учебной
работе В.С. Плевковым
с 24.01.2007
до 24.01.2012
Подписано в печать
Формат 60×84/16. Бумага офсет. Гарнитура Таймс. Печать офсет.
Уч.- изд. л. 2,73. Тираж экз. Заказ №
Изд-во ТГАСУ, 634003, г. Томск, пл. Соляная,2.
Отпечатано с оригинал-макета в ООП ТГАСУ.
634003, г. Томск, ул. Партизанская,15
3
ОГЛАВЛЕНИЕ
Введение ....................................................................................... 4
1. Кинематика точки. ................................................................... 5
1.1. Содержание задания
1.2. Векторный и координатный способы задания
движения точки .................................................................... 5
1.2.1. Уравнения движения точки ......................................... 5
1.2.2. Уравнение траектории и методы её построе-
ния.................................................................................. 6
1.2.3. Определение скорости точки по заданным
уравнениям движения в декартовой системе
координат...................................................................... 7
1.2.4. Определение ускорения точки в декартовой
системе координат......................................................... 9
1.2.5. Естественный способ задания движения точки.......... 9
1.2.6. Определение скорости и ускорения точки при
естественном способе задания её движения............... 11
1.2.7. Определение радиуса кривизны
траектории
точки.............................................................................. 13
1.3. План решения, объём задания к задаче
на тему: «Кинематика точки».............................................. 14
1.4. Примеры решения задач на тему: «Кинематика точки»
1.4.1. Задача 1 ......................................................................... 15
1.4.2. Задача 2 ......................................................................... 24
1.4.3. Задача 3 ......................................................................... 34
2. Простейшие движения твёрдого тела ..................................... 36
2.1. Поступательное движение твёрдого тела ......................... 36
2.2. Вращение твёрдого тела вокруг неподвижной оси.......... 37
2.2.1. Общие формулы угловых и линейных харак-
теристик вращательного движения............................. 37
2.2.2. Примеры решения задач.
Задача 1. ............................................................................... 42
Задача 2 ................................................................................ 47
Вопросы для самоконтроля ......................................................... 50
Библиографический список......................................................... 52
4
Кто не знаком с законами движения, тот
не может познать природы.
Г. Галилей
ВВЕДЕНИЕ
Кинематика как раздел теоретической механики рассматрива-
ет лишь геометрическую сторону механической формы движения,
не затрагивая причин, вызывающих это движение. Кинематика
предшествует динамике и этим облегчает её изложение и изучение.
Поэтому иногда кинематику рассматривают как введение в динами-
ку. Вместе с тем кинематика имеет также большое самостоятельное
значение. Особенно при проектировании и создании механизмов,
которые должны обладать определёнными, наперёд заданными ки-
нематическими характеристиками движения их звеньев или отдель-
ных точек. Это хорошо видно на примерах расчёта механизмов ро-
бототехники, выполняющих определённые (заданные) функции ро-
бота. Здесь движение отдельных звеньев должны быть строго увяза-
ны между собой во времени и пространстве.
Детальное рассмотрение геометрических характеристик дви-
жения механизмов привело к необходимости выделения одного из
разделов кинематики в отдельную дисциплину – «Теорию механиз-
мов и машин».
Цель методического указания – дать примеры решения задач с
достаточно полными пояснениями, а также необходимый теорети-
ческий материал без доказательств, но со ссылкой на рекомендуе-
мую учебную литературу.
Рассматривать геометрические характеристики движения
(уравнения движения, траекторию, скорость, ускорение) можно на
примере свободной материальной точки или точки, принадлежащей
какому-либо телу или звену механизма.
Перед тем как приступить к выполнению курсовой работы,
студент должен изучить теоретический материал и решить более
простые задачи на практических занятиях или самостоятельно. Для
этого он может воспользоваться учебной литературой, список кото-
рой приведён в конце методического указания.

5
1. КИНЕМАТИКА ТОЧКИ (К–1)
В расчётно-графической работе на эту тему рассматриваются
вопросы по составлению уравнений движения точки, нахождению
её траектории, скорости и ускорения в заданный момент времени.
Как известно, имеется три способа задания движения точки:
естественный, координатный и векторный. При выполнении расчёт-
но-графической работы воспользуемся первыми двумя.
1.1. Содержание задания
Задание К–1 включает в себя решение задач по двум разде-
лам: кинематика точки и вращение твёрдого тела вокруг неподвиж-
ной оси. Каждому студенту дается свой вариант задания, которое
студент выполняет самостоятельно. Расчет должен сопровождаться
графикой: в масштабе должна быть построена траектория движения
точки; после чего для заданного момента времени точка наносится
на траекторию. Вычислив для данного момента времени значения
векторов скоростей и ускорений, наносим их в масштабе на чертёж
в точке М траектории.
При графическом построении используются три масштаба:
линейный масштаб, масштаб скоростей и масштаб ускорений.
1.2. Векторный и координатный способы
задания движения точки
1.2.1. Уравнение движения точки
Поскольку векторный и координатный способы задания дви-
жения между собой увязаны, то мы воспользуемся общим чертежом
(рис. 1).
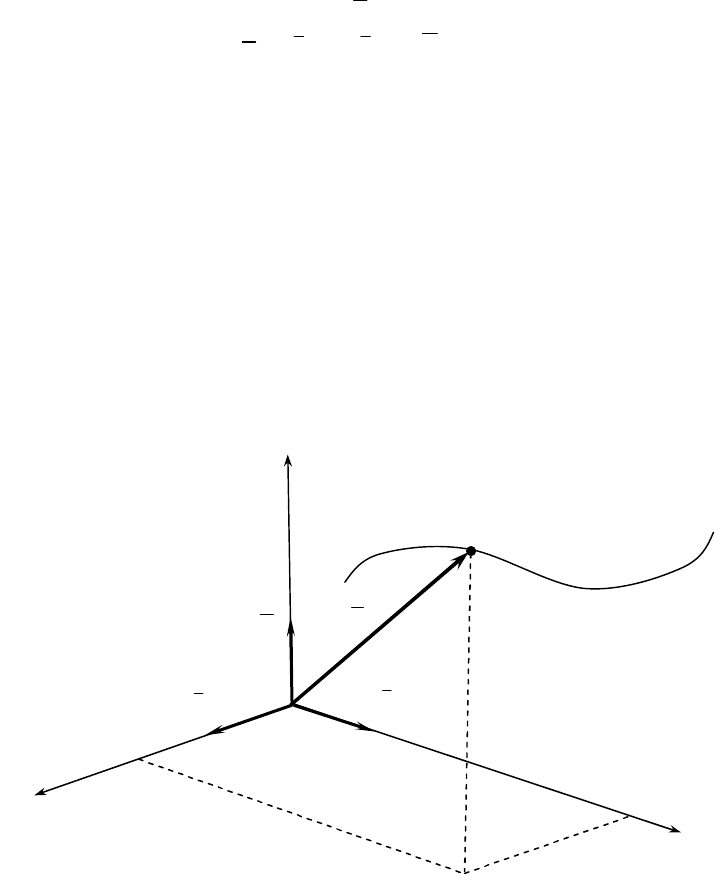
При векторном способе задания движения положение дви-
жущейся точки М определяется [1] радиусом-вектором
t
r
r
(1.1)
6
Разложим радиус-вектор
r
по осям координат:
,kzjyixr
(1.2)
где
z
y
x
,
,
– координаты движущейся точки М
в прямоугольной
системе координат.
Эти координаты являются функциями времени
t
t
f
z
t
f
y
t
f
x
321
,
,
(1.3)
и полностью определяют положение движущейся точки М в любой
момент времени.
Следовательно, они являются уравнениями движения точки М
в координатной форме.
1.2.2. Уравнение траектории и методы её построения
Отличие уравнений движения от уравнения траектории со-
стоит в том, что в последнем отсутствует аргумент t , поэтому для
нахождения аналитического уравнения траектории необходимо
совместно решить систему уравнений движения (1.3) с целью
исключения аргумента t.
Графическое построение траектории точки М может быть
произведено либо по уравнениям движения, либо по уравнению тра-
ектории. В первом случае, задавая различные значения времени t,
z
x
y
Рис. 1
k
i
j
r
M
x
y
z
траектория

7
будем находить соответствующие ему значения координат x и y
движущейся точки. Нанеся эти точки на чертёж, выполненный в
масштабе, и соединив их между собой плавной линией, получим
траекторию точки на чертеже.
Во втором случае, имея уравнение траектории точки и задавая
различные значения координат x точки, будем находить соответст-
вующие им значения координат y (или наоборот). По полученным
значениям координат x и y построим траекторию.
1.2.3. Определение скорости точки по заданным
уравнениям движения в декартовой системе
координат
Даны уравнения движения точки:
t
f
z
t
f
y
t
f
x
321
;
;
.
Скорость точки определяется по её проекциям на оси коорди-
нат [1]:
dt
dz
V
dt
dy
V
dt
dx
V
zyx
;; , (1.4)
то есть проекции скоростей точки на оси координат равны первым
производным от соответствующих координат движущейся точки по
времени.
Для нахождения модуля вектора скорости точки воспользуем-
ся формулой:
222
222
dt
dz
dt
dy
dt
dx
VVVV
zyx
(1.5)
Направление вектора скорости
V
определяется по направ-
ляющим косинусам углов, образованных вектором скорости
V
с
осями координат:
;);cos(
V
V
iV
x
;);cos(
V
V
jV
y
(1.6)
.);cos(
V
V
kV
z

8
Следует указать на то, что при правильном нахождении моду-
ля и направления вектора скорости
V
в заданной точке, мы получим
совпадение направления вектора
V
с касательной к траектории в
заданный момент времени
t
(рис. 2).
x
x
y
y
z
z
O
a
j
a
y
i
a
x
M
ka
z
Рис. 3
x
y
z
O
M
x
y
z
V
kV
z
j
V
y
i
V
x
Рис. 2
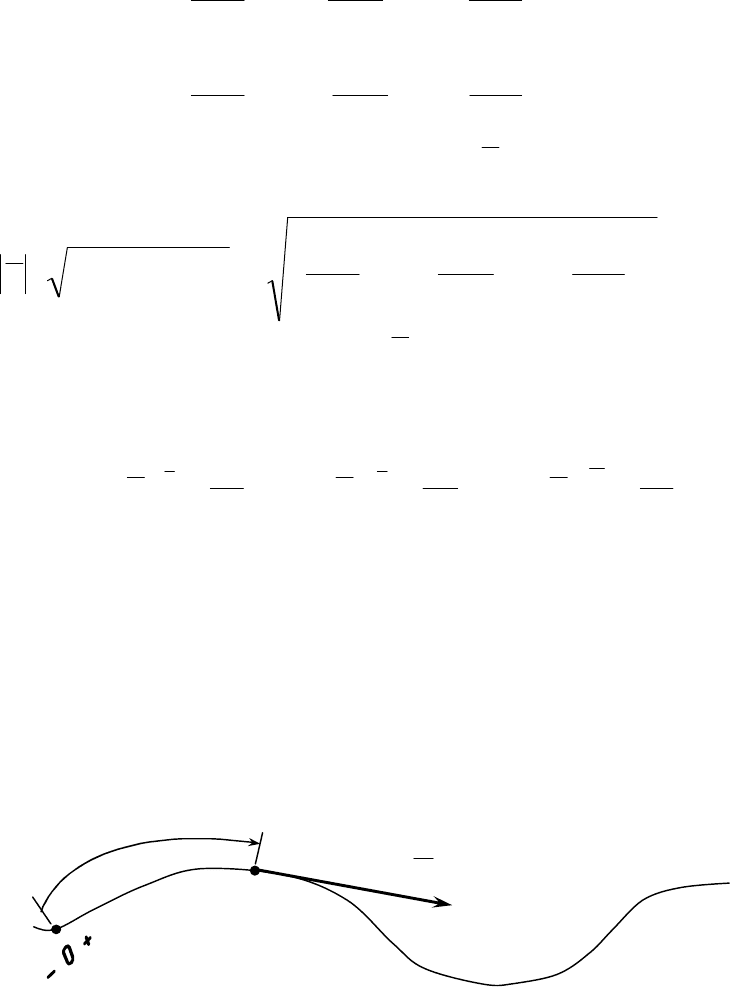
9
1.2.4. Определение ускорения точки в декартовой системе
координат
Из учебной литературы [1, 2] известно, что проекции ускоре-
ния точки в декартовой системе координат определяются как пер-
вые производные по времени от проекций вектора скорости на со-
ответствующие оси координат:
.;;
или,;;
2
2
2
2
2
2
dt
zd
a
dt
yd
a
dt
xd
a
dt
dV
a
dt
dV
a
dt
dV
a
zyx
z
z
y
y
x
x
(1.7)
Модуль вектора ускорения точки
a
определим через его про-
екции на оси координат по формуле:
2
2
2
2
2
2
2
2
2
222
dt
zd
dt
yd
dt
xd
aaaa
zyx
(1.8)
Направление вектора ускорения
a
определяется при помощи на-
правляющих косинусов углов, образованных вектором ускорения с
осями координат (рис. 3):
a
a
ka
a
a
ja
a
a
ia
z
y
x
;cos;;cos;;cos . (1.9)
1.2.5. Естественный способ задания движения точки
При естественном способе задания движения точки задаётся
траектория, начало отсчёта, направление отсчёта. Тогда положение
движущейся точки может быть определено при помощи дуговой ко-
ординаты
tfS
(рис. 4).
S
V
траектория
Рис. 4

10
Рис. 5
