Лысак О.Н. (сост.) Кинематика точки и простейшие движения твёрдого тела
Подождите немного. Документ загружается.


11
Три взаимно перпендикулярные плоскости соприкасающаяся,
нормальная и спрямляющая (рис. 5) образуют сопутствующий трёх-
гранник. Рёбра сопутствующего трёхгранника часто принимают за
естественные оси координат: касательную, главную нормаль и би-
нормаль.
За положительные направления на рёбрах сопутствующего
трёхгранника принимают направления следующих единичных век-
торов:
1) основной вектор касательной
. Он направлен по каса-
тельной в сторону возрастания параметра. Если за параметр принять
время t , то направление
совпадает с направлением движения точ-
ки по траектории. Если параметром служит дуга, то направление
совпадает с направлением отсчёта положительных дуг;
2) основной вектор главной нормали
n
. Он направлен по
главной нормали в сторону вогнутости траектории. Направление
n
не зависит от выбора параметра, т.е. имеет объективный геометри-
ческий смысл;
3) основной вектор бинормали
b
. Он направлен так, чтобы
тройка векторов bn
,,
была правой.
На рис. 5 показано положение этих осей и плоскостей для
двух различных моментов времени.
1.2.6. Определение скорости и ускорения точки
в криволинейном движении при естественном
способе задания её движения
Алгебраическая величина вектора скорости
V
определяется
как первая производная от дуговой координаты
S
по времени:
dt
dS
V . (1.10)
Направление вектора скорости совпадает с касательной к тра-
ектории (рис. 4).
Вектор ускорения точки лежит в соприкасающейся плоскости
(поэтому проекция ускорения на бинормаль равна нулю a
b
=0) и ра-
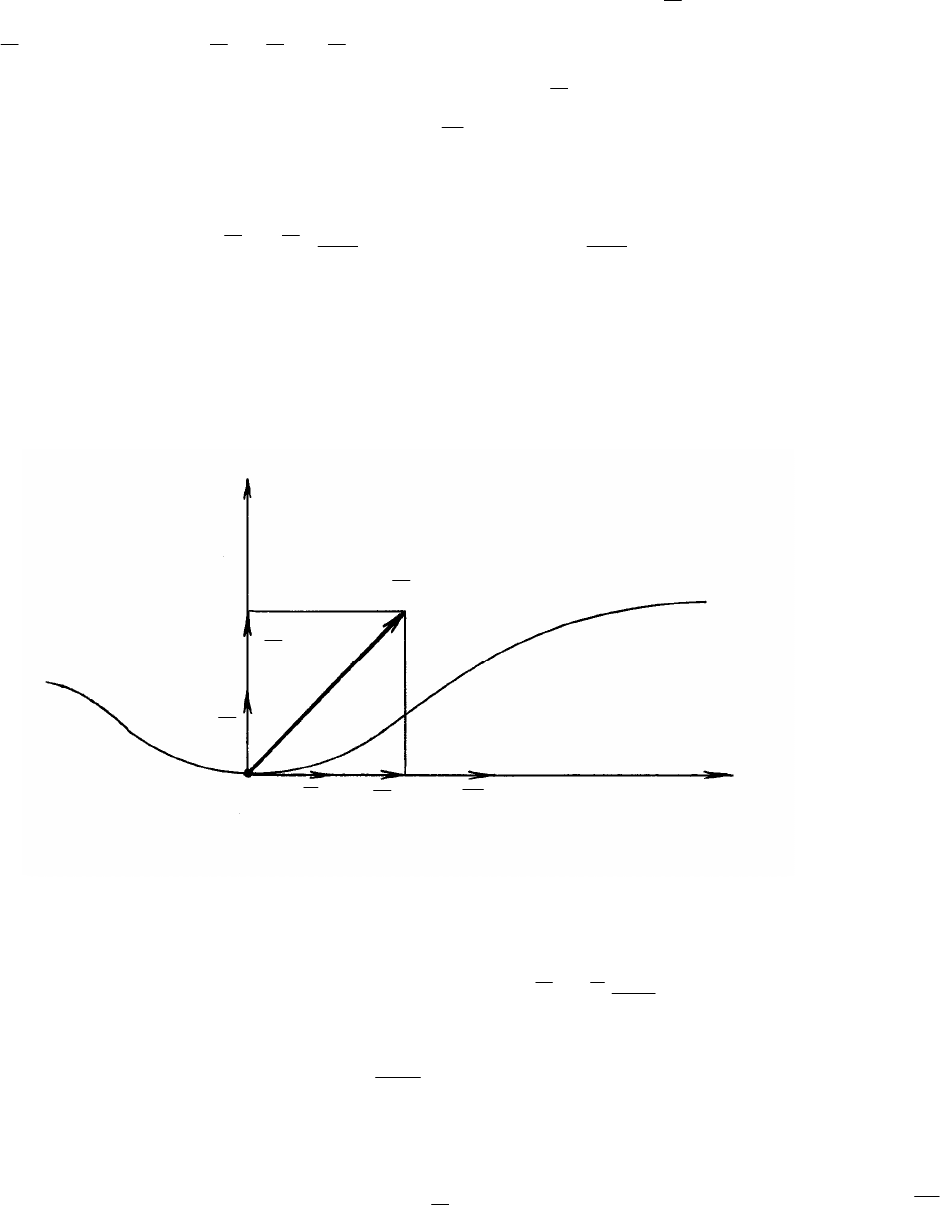
12
вен векторной сумме ускорений нормального –
n
a
и касательного –
a
(рис. 6)
a
a
a
n
. (1.11)
Вектор нормального ускорения
n
a
характеризует изменение
направления вектора скорости
V
за единицу времени и направлен
по главной нормали в сторону вогнутости траектории
ρ
2
V
na
n
; модуль
ρ
2
V
a
n
, (1.12)
где
ρ
– радиус кривизны траектории в точке М (рис. 6).
Вектор касательного ускорения
dt
dV
a
; алгебраическая
величина вектора
dt
dV
a
. (1.13)
Касательное ускорение характеризует изменение модуля век-
тора скорости за единицу времени и направлено по касательной к
траектории в точке М. Вектор
a
совпадает с вектором скорости
V
в том случае, когда движение точки ускоренное, и направлен в про-
тивоположную сторону в случае замедленного движения.
Касательное ускорение может быть определено по другой
формуле:
касательная
главная нормаль
М
n
n
a
a
V
a
Рис. 6
13
V
aVaV
a
yyxx
. (1.14)
При подсчёте ускорения по этой формуле надо быть внима-
тельным и учитывать все знаки проекций скоростей и ускорений на
оси координат. Если в случае подсчёта получим значение
a
со
знаком плюс, то движение ускоренное, и вектор
a
будет направлен
по направлению вектора скорости
V
; если
a
принимает отрица-
тельное значение, то движение точки замедленное, и вектор
a
на-
правлен противоположно вектору скорости
V
.
Модуль вектора ускорения
a
:
22
aaa
n
. (1.15)
1.2.7. Определение радиуса кривизны
ρ
траектории точки
Из формулы (1.12) следует,
n
a
V
2
ρ . (1.16)
Модуль вектора скорости
V
вычисляем по формуле (1.5),
нормальное ускорение из формулы (1.15). Получаем
22
aaa
n
; тогда окончательно получим:
2
222
222
ρ
dt
dV
aaa
dt
dz
dt
dy
dt
dx
zyx
. (1.17)
Подставляя заданное значение времени
t
, находим модули
векторов
V
и
n
a
, после чего находим значение радиуса кривизны
ρ
траектории точки для заданного момента времени
t
.
14
1.3. План решения, объём задания к задаче
на тему: «Кинематика точки»
1.3.1. Записать условия заданного варианта задачи.
1.3.2. Изобразить механизм (или движущееся тело) и заданную
точку в произвольный момент времени
t
(но не в начальный).
1.3.3. Выбрать неподвижную прямоугольную систему коорди-
нат.
1.3.4. Найти (составить) уравнения движения заданной точки М.
Для этого текущие координаты точки необходимо выразить как
функции времени, увязав их (координаты) с геометрическими раз-
мерами и положением механизма в изображённом на чертеже поло-
жении.
1.3.5. Найти уравнение траектории заданной точки М механизма.
1.3.6. Построить траекторию точки М графически, используя масштаб.
1.3.7. Вычислить проекции вектора скорости
V
на оси коорди-
нат для произвольного момента времени
t
. Затем найти модуль и
направление вектора
V
для заданного момента времени
t
1
.
1.3.8. Вычислить проекции вектора ускорения
a
на оси коор-
динат для произвольного момента времени
t
. Найти модуль и на-
правление вектора
a
для заданного момента времени
t
1
.
1.3.9. Вычислить нормальное, касательное и полное ускорение
a
движущейся точки в естественной системе координат для задан-
ного момента времени
t
1
.
1.3.10. Вычислить значение радиуса кривизны
ρ
траектории
движущейся точки для заданного момента времени
t
1
.
1.3.11. Для заданного момента времени
t
1
нанести на траектории
в точке М в масштабе векторы скорости
V
, ускорения
a
, а также
их проекции на оси координат
x
V
(
,
y
V
,
x
a
,
y
a
,
n
a
,
a
).
Примечание. При графическом построении необходимо исполь-
зовать три масштаба: линейный масштаб, масштаб скоростей, мас-
штаб ускорений.
1.3.12. Для заданного момента времени
t
1
нанести на чертеже (в
масштабе) радиус кривизны
ρ
. Показать положение центра кривиз-
ны.
15
1.4. Примеры решения задач на тему:
«Кинематика точки»
1.4.1. Задача 1
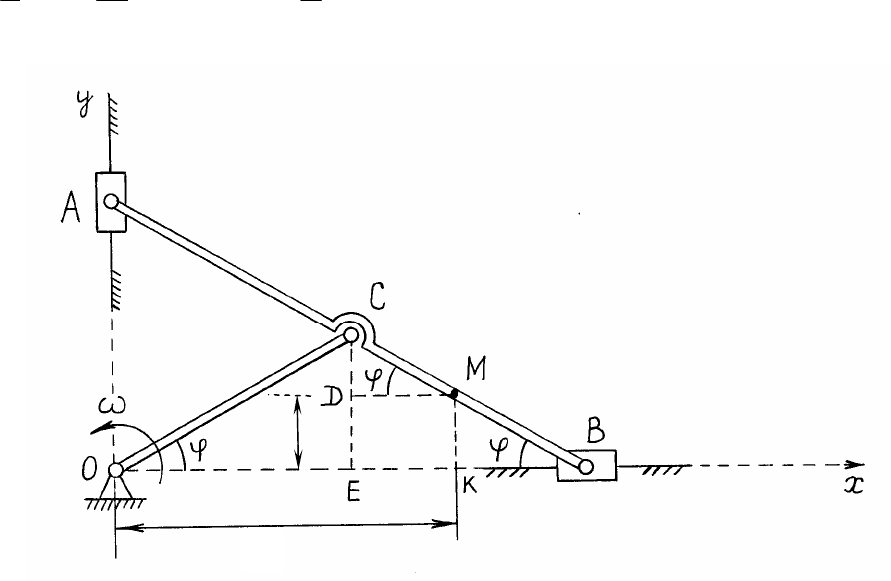
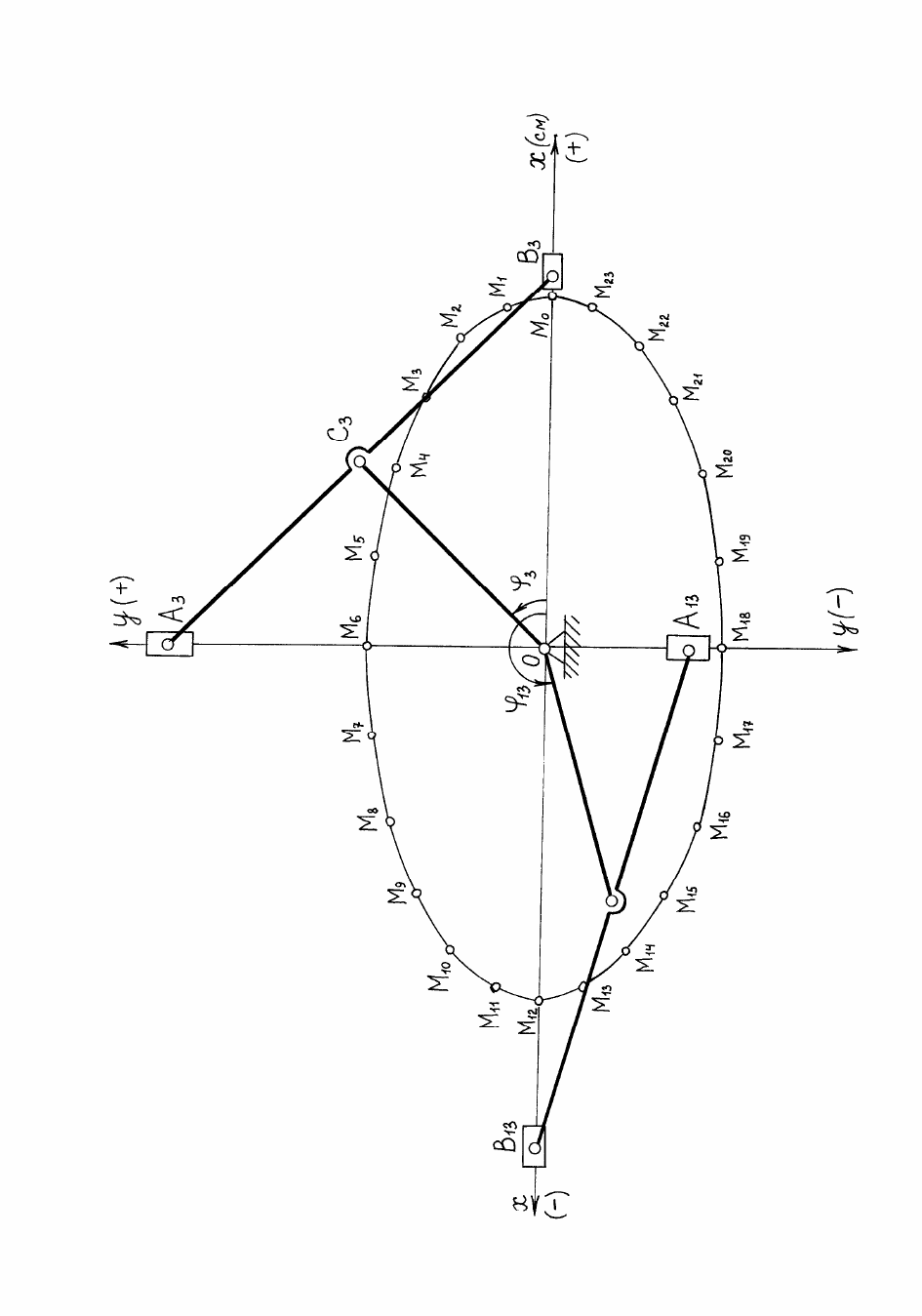
Механизм эллипсографа состоит из кривошипа ОС , линейки
АВ, ползунов А и В (рис. 7).
Кривошип вращается равномерно вокруг неподвижного цен-
тра О и приводит в движение линейку АВ. Решить задачу согласно
заданию, приведённому выше в (1.3.), для двух моментов времени
с
2
1
и с
6
13
, если: ;
2
t
см
10
;
см
30
СМ
l
СВ
АС
ОС
.
Рис. 7
Изобразим механизм в произвольный момент времени
t
(только не в начальный). Выберем начало координат в неподвижной
точке О. Для определения координат движущейся точки М в зави-
симости от заданных значений размеров и переменного угла
про-
изведём дополнительные построения на чертеже. Проведём прямые
СДЕ и МК параллельные оси Оy и прямую ДМ параллельную оси
Оx. При этом, с учётом заданных размеров звеньев механизма, по-
лучим на чертеже углы СДМ =
и МКВ =
. После чего коор-
динаты точки М можно выразить так:
M
x
M
y

16
coscos СМОСДМОЕЕКОЕОКx
M
;
sinsin СМОССДСЕДЕМКy
M
.
Подставляя заданные в условиях задачи значения, получим
.
2
sin20
,
2
cos40
ty
tx
M
M
(1.18)
Это уравнения движения точки М в прямоугольной системе
координат.
Для определения уравнения траектории точки, решим совме-
стно уравнения движения и исключим аргумент
t
. Для этого урав-
нения представим в следующем виде, разделив первое из них на 40,
а второе на 20:
.
2
sin
20
,
2
cos
40
t
y
t
x
M
M
Возведя в квадрат левые и правые части этих уравнений, сло-
жим их. В результате получим уравнение траектории точки М:
.1
20
40
2
2
2
2
MM
yx
Это уравнение эллипса с полуосями 40 см по оси
Ox
и 20 см
по оси
Oy
, с центром в начале координат.
Для графического построения траектории точки М можно
воспользоваться одним из методов, приведённых выше в 1.2.2. В
этой задаче воспользуемся одним из них.
Из уравнений (1.18), задавая различные значения моментов
времени
t
, будем находить координаты
M
x
и
M
y
для соответст-
вующих значений
t
. В нашей задаче промежутки времени, отде-
ляющие один момент времени от другого, возьмём равным 1/6 с.
Примечание. Для более точного графического построения
траектории точки необходимо промежутки времени брать неболь-
шими.
Подсчёт значений координат точки М.
17
,
2
cos40 tx
M
.
2
sin20 ty
M
Будем в эти уравнения подставлять значения
t
:
.c4
6
24
;c
6
6
;c
6
5
;c
6
4
;c
6
3
;c
6
2
;c
6
1
;0
246543210
tttttttt
При:
0
0
t
,см400cos40
2
cos40
00
tx
;см00sin20
2
sin20
00
ty
c
6
1
1
t
,см6,3815cos40
12
cos40
6
1
2
cos40
0
1
x
.см2,5
12
sin20
6
1
2
sin20
1
y
Точно так же будем подсчитывать координаты движу-
щейся точки вплоть до получения полного замкнутого эллипса (до
момента
c
4
24
t
).
Полученные значения координат сведём в таблицу:
Значения
t
,с
0
6
1
6
2
6
3
6
4
6
5
6
6
Точка М
0
М
1
М
2
М
3
М
4
М
5
М
6
x
М
, см +40 +38,6 +34,64
+28,28
+20 +10,36
0
y
М
, см 0 +5,2 +10 +14,14
+17,32
+19,32
+20
6
7
6
8
6
9
…
6
13
…
6
24
М
7
М
8
М
9
М
13
М
24
-10,36 -20 -28,28 -38,64 +40
+19,32
+17,32
+14,14
-5,18 0
Выбирая линейный масштаб, наносим на чертеже последова-
тельно положения точки, используя полученные значения координат
(рис. 8). Соединив точки на чертеже плавной линией, получим тра-
екторию (эллипс).
18
Рис. 8. Построение тр
аектории точки М
механизма элли
псографа
19
Примечание. Учитывая, что эллипс – кривая, симметричная
относительно своих главных осей, достаточно рассчитать ¼
часть эллипса. Область изменения угла φ (аргумент синуса и коси-
нуса) : .
2
0
Будем задавать значения угла φ через каждые 10
градусов, т.е.
18
/
рад (при этом в данной задаче
9
/
1
t
с).
Остальные ¾ части эллипса достраиваются симметрично.
Определение скорости точки М.
Используя формулы (1.4), определим проекции вектора ско-
ростей точки М на оси координат.
.
2
cos10
)
2
sin20(
,
2
sin20
)
2
cos40(
t
dt
td
dt
dy
V
t
dt
td
dt
dx
V
M
y
M
x
Для момента времени
45рад
42
1
2
;c
2
1
33
tt ,
;см/с43,44,)см/с(14,14
2
2
20
xx
VV
;см/с21,22,см/с07,7
2
2
10
yy
VV
,см/с67,4921,2243,44
22
22
yx
VVV
.
см/с
67
,
49
3
t
V
Для момента времени )рад(
12
13
6
13
2
;c
6
13
1313
tt ,
,259,015sin195sin,195
000
13
.966,015cos195cos
00
Тогда в момент времени
t
t
13
:
см/с
26
,
16
18
,
5
259
,
0
20
x
V
,
см/с
34
,
30
966
,
0
10
y
V
.

20
Модуль вектора скорости :
;см/с43,3434,3026,16
22
22
yx
VVV
см/с
43
,
34
13
t
V
.
Изобразив (рис. 9) в масштабе траекторию точки М, нанесём
на этой траектории её положения в моменты
c
2
1
3
t
и
c
16
13
13
t
:
(М
3
и М
13
). Далее, от полученных точек М
3
и М
13
отложим проек-
ции скоростей на оси координат с учётом знаков в масштабе скоро-
стей m
V
1см 10 см/с. Затем строим параллелограммы и получаем
векторы скоростей в этих точках.
При правильном вычислении векторы скоростей должны
быть направлены по касательной к траектории в сторону дви-
жения точки М.
Определение ускорения точки М
Находим проекции вектора ускорения точки М по формуле
(1.7):
.
2
sin5
2
cos10
,
2
cos10
2
sin20
2
2
t
dt
td
dt
dV
a
t
dt
td
dt
dV
a
y
y
x
x
Точка М
3
, при )45(
4
2
1
2
2
;c
2
1
0
333
ttt :
;см/с79,69
4
cos14,310
22
x
а
;)см/с(89,34
4
sin14,35
22
y
a
22222
см/с03,78)89,34()79,69(
yx
aaa .
Точка М
13
, при
:195
12
13
6
13
2
;c
6
13
0
1313
радtt
22
см/с33,95966,010
x
a ;
