Лысак О.Н. (сост.) Кинематика точки и простейшие движения твёрдого тела
Подождите немного. Документ загружается.

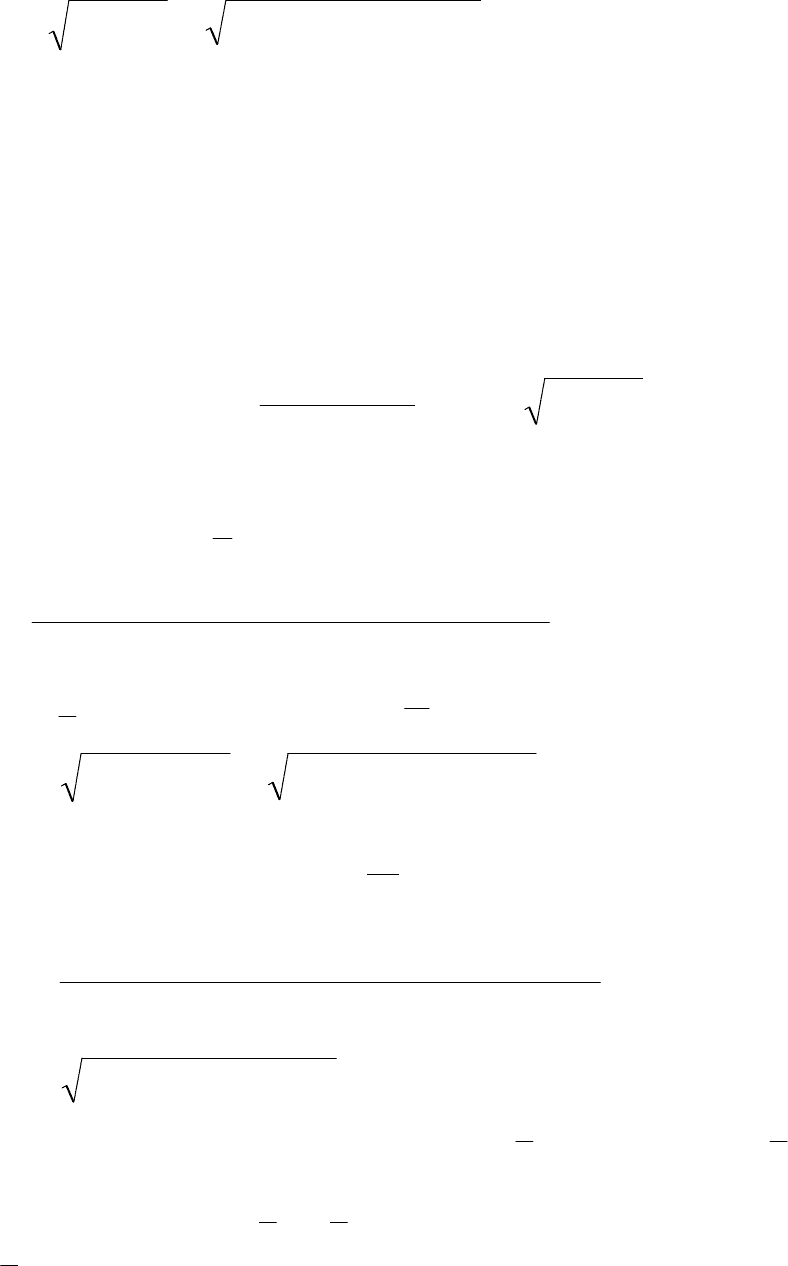
21
)см/с(77,12)26,0(5
22
y
a ,
22222
см/с18,96)77,12()33,95(
yx
aaa .
Полученные значения модулей векторов ускорений и их про-
екций на оси координат для моментов
t
3
и
t
13
отложим соответствен-
но в точках М
3
и М
13
траектории (рис. 9).
Определение ускорения точки М в естественной системе
координат
Для этого воспользуемся формулами (1.11); (1.14); (1.15).
Так как точка М движется в плоскости (
xOy
), то проекции
z
V
и
z
a
равны нулю. Тогда
V
aVaV
a
yyxx
,
22
aaa
n
.
Подставляя найденные выше значения для
yxyx
a
a
V
V
;
;
;
для
момента времени ,c
2
1
3
t найдём
2
см/с83,46
67,49
89,3421,2279,69)43,44(
a .
Знак плюс показывает, что точка движется ускоренно, следователь-
но, вектор
a
направлен по вектору
V
.
2
2222
см/с42,6283,4603,78
aaa
n
.
Для момента времени c
6
13
13
t (для точки М
13
)
2
см/с77,33
43,34
77,1234,3033,9526,16
a ,
06,90)77,33()18,96(
22
n
a (см/с
2
).
Отложив на траектории нормальное
n
a
и касательное
a
ус-
корения в точках М
3
и М
13
, произведя их векторное сложение, по-
строив прямоугольники (
a
a
n
), получим значения векторов уско-
рений
a
. Как видно из рис. 9, эти векторы по модулю и по напра-

22
Линейный масштаб m 1: 4
Масштаб скоростей m
V
1 см ÷ 10 см/с
Масштаб ускорений m
a
1 см ÷ 10 см/с
2
Рис. 9
Траектория движения точки М.
Векторы скоростей и ускорений точки М
в моменты t
3
и t
13
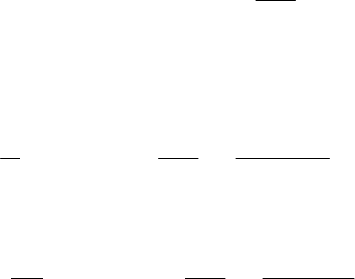
23
влению совпадают с векторами ускорений, полученными при коор-
динатном способе задания движений точки.
Нахождение радиусов кривизны траектории в точках М
3
и
М
13
.
Из формулы (1.16)
n
a
V
2
. Подставив значения
V
и
n
a
,
найдём радиус кривизны для моментов
t
3
и
t
13
.
Для
;см52,39
42,62
67,49
;c
2
1
22
33
n
a
V
t
для
.см16,13
06,90
43,34
;c
6
13
22
1313
n
a
V
t
На чертеже (рис. 9) отложим от точек М
3
и М
13
по главным
нормалям в сторону вогнутости траектории значения
3
и
13
и от-
метим точки О
3
и О
13
– центры кривизны траектории в этих точках.
Для наглядности из этих точек проведём окружности с радиу-
сами
3
и
13
. Эти окружности будут иметь одинаковую кривизну с
кривизной траектории, соответственно, в точках М
3
и М
13
.
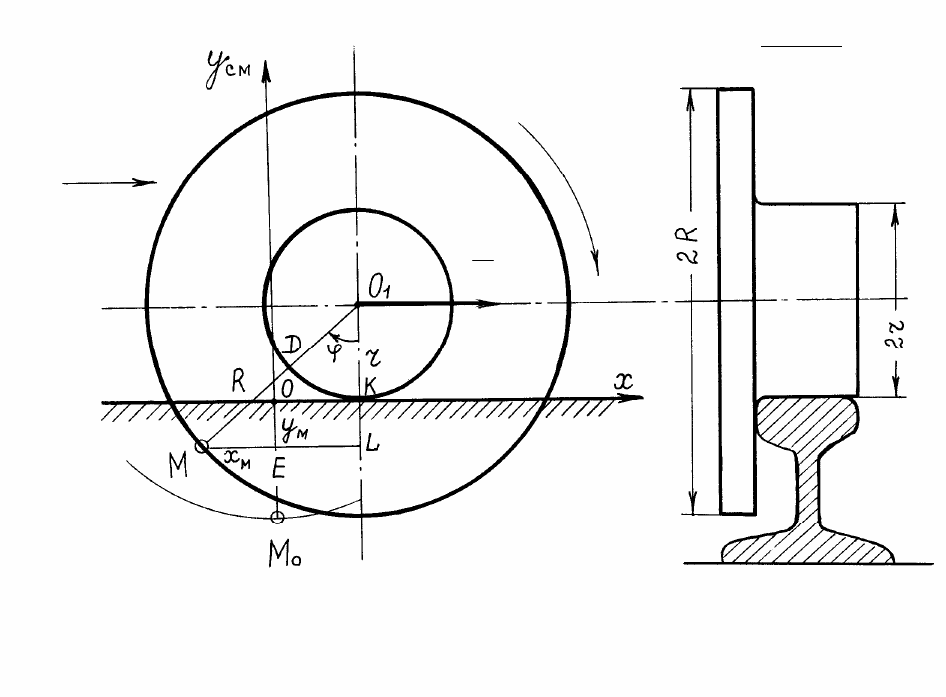
24
1.4.2. Задача 2
Колесо радиуса
м
1
,
0
r
, имеющее реборду радиуса
м
4
,
0
R
, катится без скольжения по прямолинейному рельсу
(рис.10) с постоянной скоростью
м/с
20
V
. В начальный момент
времени
0
0
t
с точка М находилась в наинизшем положении М
о
,
тогда центр колеса О
1
находился на оси Oy и угол
0
.
Требуется определить уравнения движения точки М, лежащей
на ободе реборды, её скорость, ускорение полное, нормальное и ка-
сательное в различные заданные моменты времени
1484
;
;
t
t
t
.
Необходимо также построить графически в масштабе траек-
торию точки М; найти и нанести на чертёж радиусы кривизны тра-
ектории точки М для моментов времени
1484
;
;
t
t
t
.
А
Вид А
V
Рис. 10
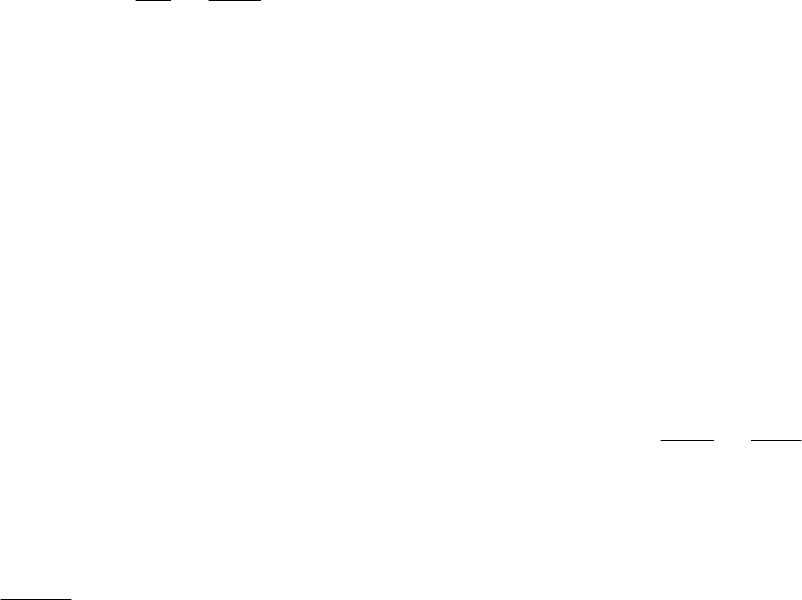
25
Составление уравнений движения точки М
Для нахождений уравнений движения (
tfx
М
1
и
tfy
M
2
) необходимо механизм (в данном случае колесо) сдви-
нуть из начального положения, изобразить на чертеже. За начало
координат примем точку соприкосновения колеса малого радиуса
r
.
Точка М при этом будет занимать наинизшее положение – М
0
(рис.10). Установим зависимость координат
x
и
y
точки М от по-
ложения центра колеса О
1
и угла поворота
(рис. 10).
На чертеже видно, что в этот момент
.cos
,sin
11
rRKOLOKLOEy
RtVLMOKMEx
M
M
Так как колесо катится без проскальзывания, то перемещение
колеса (отрезок ОК) будет равен длине дуги ДК радиуса
r
.
OК
ДК
.
Но
t
V
ОК
– путь, пройденный центром колеса
при равномерном движении, а длина дуги
r
ДК
; т.е.
r
t
V
,
отсюда
.радиан002
1,0
20
t
t
r
tV
(1.19)
Подставляя значение
t
200
в выражение для
M
x
и
M
y
, получим
уравнения движения точки М:
.м200cos4,01,0
;м200sin4,020
ty
ttx
M
M
(1.20)
Построение траектории точки М графическим способом
Способ 1. Как видно из (1.19), за время c
100
200
2
T ко-
лесо повернётся на угол
2
, следовательно, точка опишет полный
виток траектории. Разобьём этот промежуток на 24 части с шагом
c
2400
t . Будем подставлять последовательные моменты време-

26
ни в уравнения движения (1.20). Полученные координаты последо-
вательно откладываем на осях Ox и Oy; соединяя полученные точки
плавной кривой, получим траекторию точки М, описанную за один
оборот колеса. Заметим, что общий вид траектории не зависит от
скорости движения колеса.
Способ 2. Он состоит в последовательном графическом по-
строении (в масштабе) на чертеже механизма (колеса) через равные
промежутки времени. В каждом из положений колеса на чертеже
наносится точка М.
Сделаем разбивку времени на равные промежутки времени
t
. Примем этот промежуток времени c
2400
t . После чего оп-
ределим моменты времени
,
;
;
;
;
3210
t
t
t
t
для которых будем нахо-
дить последовательные положения точки М (М
0
, М
1
, М
2
, . . . ), кото-
рые нанесём на чертеже.
c
1200
2400
2400
;c
2400
;0
12010
ttttttt
и далее .c
1200
7
;;c
300
;;c
600
;c
800
14843
tttt
Для сокращения изложения, в качестве примера, определим
положения точки М лишь в двух положениях: при
4
t
t
(точка М
4
)
и при
t
t
14
(точка М
14
).
При c
600
4
tt
м1047,0
600
2020
4
tS ,
.60рад
3
600
200200
4
t
Построение: переместим колесо по оси
x
на расстояние
м
1047
,
0
4
S
(рис. 11), начертим колесо на чертеже, далее отло-
жим угол
0
4
60 от начального положения, найдём точку M
4
и
нанесём её на чертеже.
Точно так же для точки М
14
в момент :c
1200
7
14
tt
м366,0
1200
7
2020
14
tS ,

27
m 1:5
Рис. 11.
Построение траектории точки М
28
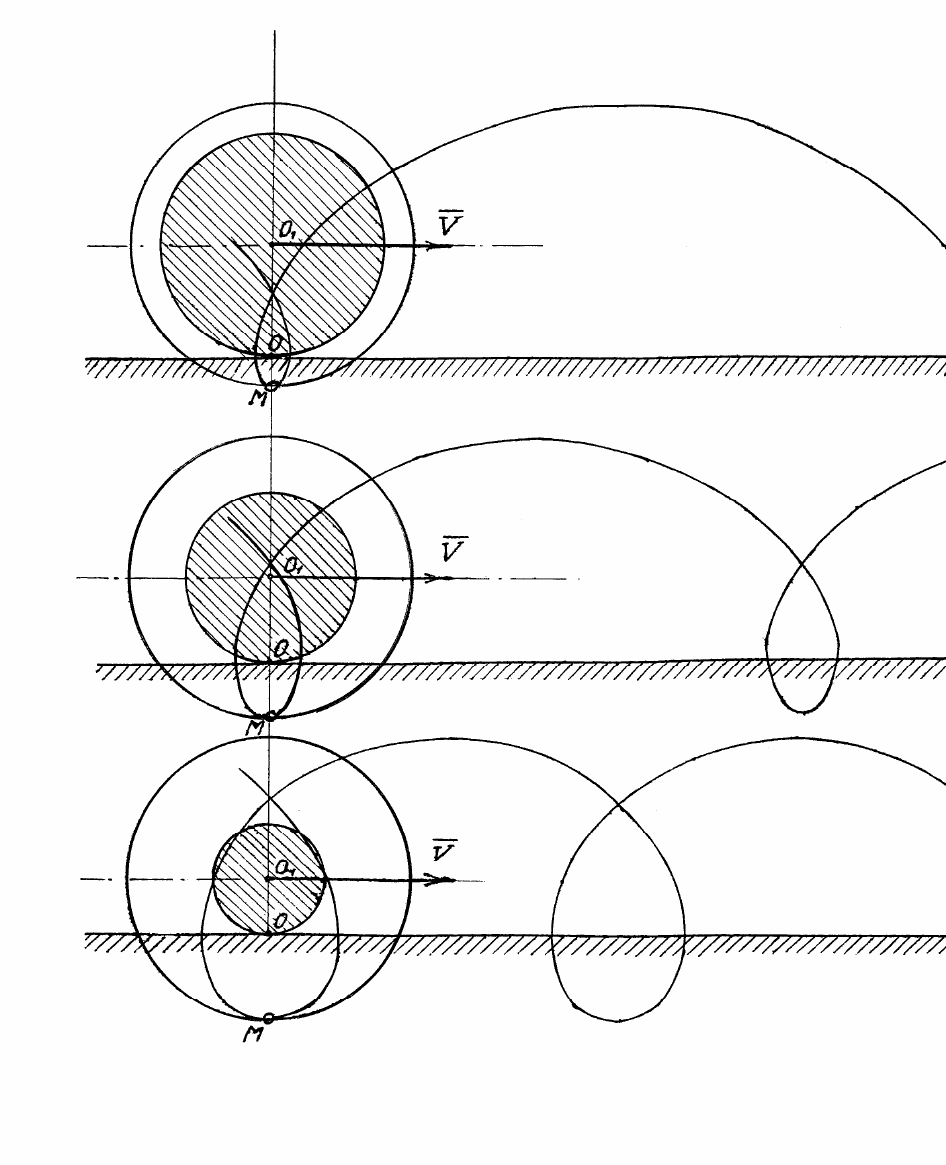
Рис. 12.
Влияние соотношения радиусов колёс на траекторию
движения точки М обода большого колеса
29
.210рад
12
14
1200
7
200200
0
14
t
Отложим по оси
x
путь
S
14
, пройденный колесом за с
1200
7
14
tt –
м
366
,
0
14
S
,
отложив угол
0
14
210
, найдём положение точки М
14
.
Точки М
0
, М
1
, М
2
, М
3
, . . . ,М
14
, . . . , в порядке последователь-
ности нанесённые на чертёж и соединённые плавной линией, обра-
зуют траекторию движения точки М катящегося колеса. Напомина-
ем – качение происходит без проскальзывания.
Для наглядности на рис. 12 приведены траектории движения
точек для колёс с различным соотношением радиусов колёс. Траек-
тории рассчитаны и нанесены на чертёж с учётом масштаба.
Определение скорости точки М для моментов времени
1484
,
,
t
t
t
Проекции скорости точки М на оси координат находим по
первым производным от уравнений движения:
.м/с200sin80
200cos4,01,0
;м/с200cos8020
200sin4,020
t
dt
td
dt
dy
V
t
dt
ttd
dt
dx
V
M
y
M
x
Точка М
4
.
0
444
60рад
3
600
200200;c
600
tt ,
Тогда,
;м/с20
3
cos8020
x
V
;)м/с(28,69
3
sin80
y
V
.м/с11,7228,69)20(
2222
4
yx
VVV
Точка М
8
.
0
888
120рад
3
2
200;c
300
tt ,
Тогда,
;м/с60
3
2
cos8020
x
V
;)м/с(28,69
3
2
sin80
y
V

30
м/с65,9128,6960
2222
8
yx
VVV .
Точка М
14
.
0
141414
210рад
6
7
200;c
1200
7
tt ,
;м/с28,8928,6920
6
7
cos8020
x
V
;)м/с(40
6
7
sin80
y
V
м/с83,97)40(28,89
2222
14
yx
VVV .
Полученные значения проекций скоростей с учётом их знаков
откладываем в масштабе в точках М
4
, М
8
, М
14
; затем в этих точках
(рис. 13) строим параллелограммы и получаем векторы скоростей в
этих точках:
V
V
V
4 8 14
,
,
.
На рисунке видно, что векторы скоростей
направлены по касательным к траекториям в точках М
4
, М
8
и М
14
,
что подтверждает правильность расчётов.
Примечание. Траектория на рис. 13 взята с рис. 11. Для того
чтобы не затемнять чертёж, окружности радиуса R не показаны, но
показано колесо радиуса
r
в четырёх положениях.
Определение ускорения точки М для моментов времени
1484
,
,
t
t
t
Проекции ускорения точки М на оси координат находим по
первым производным от проекций скорости на соответствующие
оси координат:
.м/с200cos160
200sin80
,м/с200sin160
200cos8020
2
2
t
dt
td
dt
dV
а
t
dt
td
dt
dV
а
y
y
x
x
Точка М
4
. .60,002
0
444
t
,м/с805,016060cos160
,м/с56,138866,016060sin160
20
20
y
x
а
а
22222
4
м/с1608056,138
yx
ааа .
Точка М
8
. .120,002
0
888
t
