Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.

Dynamics
155
z
A
4t
x
=
R,
COS
e
'\
r
=
R,i
+
Z,k
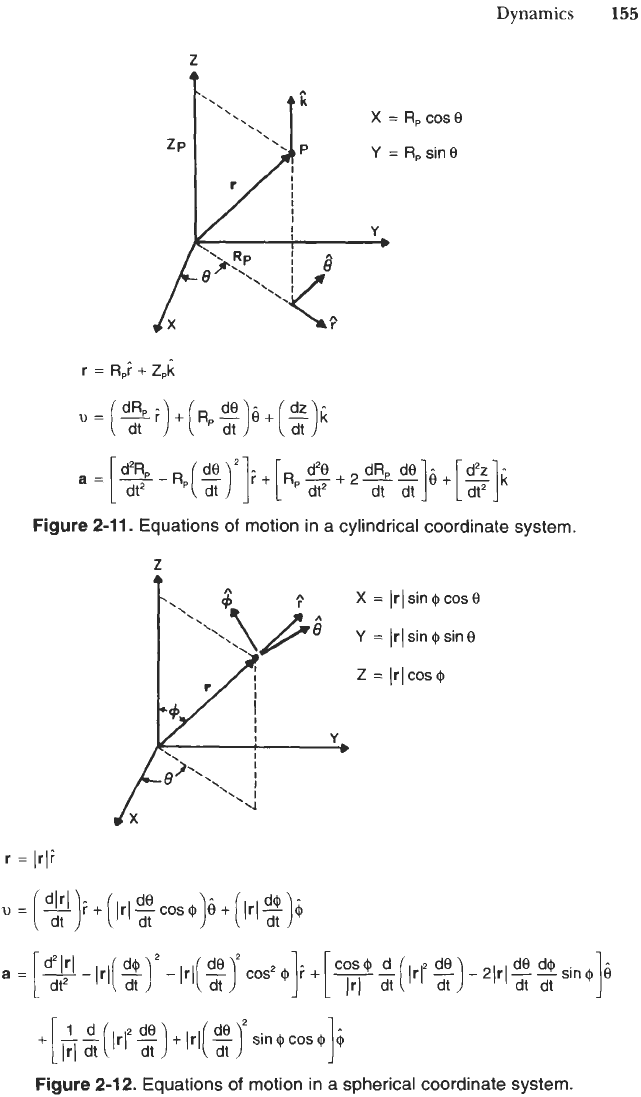
Figure 2-11.
Equations
of
motion in a cylindrical coordinate
z
A
system.
X=
Y=
Z=
)r
1
sin
Q
cos
e
lr(
sin
Q
sin
e
Irl
cos
Q
Figure 2-12.
Equations
of
motion in a spherical coordinate system.
156
General Engineering and Science
(C
1
(d)
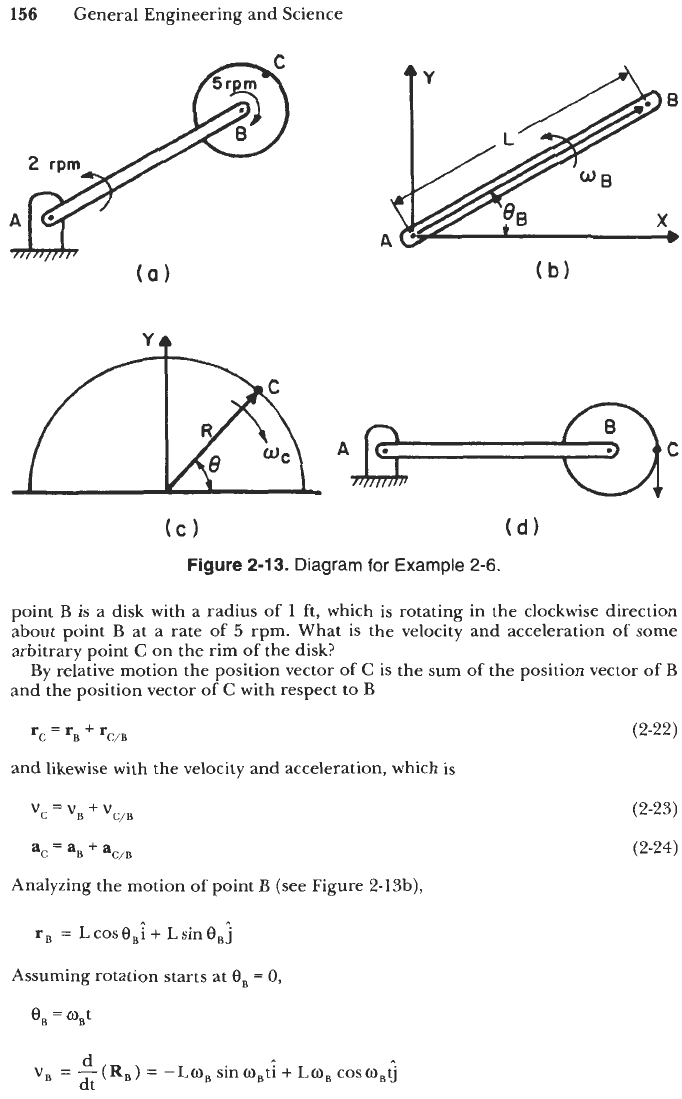
Figure
2-13.
Diagram for Example
2-6.
point
B
is a disk with a radius of 1 ft, which is rotating in the clockwise direction
about point B at a rate
of
5
rpm. What is the velocity and acceleration
of
some
arbitrary point
C
on the rim of the disk?
By relative motion the position vector
of
C
is the sum of the position vector of B
and the position vector of
C
with respect to B
rC
'B
-k
'C/B
(2-22)
and likewise with the velocity and acceleration, which is
v,
=
v,
+
VC/,
=
+
'C/B
Analyzing the motion
of
point
B
(see Figure 2-13b),
rB
=
LcosB,i+ LsinB,j
Assuming rotation starts at
8,
=
0,
8,
=
O,t
(2-23)
(2-24)
d
dt
v,
=
-(R,)
=
-LO,
sinO,ti
+
LO,
COSO,~~

Dynamics
157
d
dt
aH
=
--(vH)
=
-LO;
cosw,ti
-
LW;
sinw,ij
Assuming point
B
is fixed and analyzing the motion
of
point
C
with respect to
B
(see
Figure 2-13c),
r(
=
RcosO,i+RsinO,j
V,
,,
=
-
Rw,
sin w, ti
+
Rw, cos
w,
tj
a,
,,
=
-R~E
cosw,,tl+
RW:
sin
w,,tj
Thus
the velocity
of
point
C
is
v,
=
v,,
+
v,:,,,
=
-(La, sinw,t
+
Rw,: sinw,:t)i
+
(Lw,
cosw,t
+
Rw,: cosw,t)j
2rev 1minI 2nr
min
1
60s
I
revolution
w,
= =
0.209rps
w<
=
-0.524 rps
Rw,
=
-0.524
ft/S
V,
=
-[0.418sin(0.209t)
-
0.524sin(-0.524t)]i
+
[
0.418c0s( 0.209 t
)
-
0.524 cos(
-0.524
t
)]
3
At
t
=
0,
for
instance, the velocity is (see Figure 2-13d)
V,
=
-O.lOSjft/s
Likewise, the general expression for the acceleration of point
C
is
a,
=
a,,
+a,
,
=
-(LO;
cosw,t
+
Ro: cosw,t)i
-
(LO:,
sin
w,.t
+
RO:. sinw,
t)'j
At
t
=
0
this reduces
to
a,
=
-(
L
wi
+
Rw:
)I
=
-[
2
x
0.209'
+
1
x
(-0.524)*]3
158
General Engineering and Science
a,
=
-0.3621 ft/s2
When looking for the velocities of points on a rigid body, the method
of
instantaneous centers
can often be used. If the velocity of two points on the body are
known, those points and all other points
on
the body can be considered to be rotating
with the same angular velocity about some motionless central point. This central
point is called the instantaneous center of zero velocity. The instantaneous center
generally moves through space as a function of time and has acceleration. It does
not
represent a point about which acceleration may be determined.
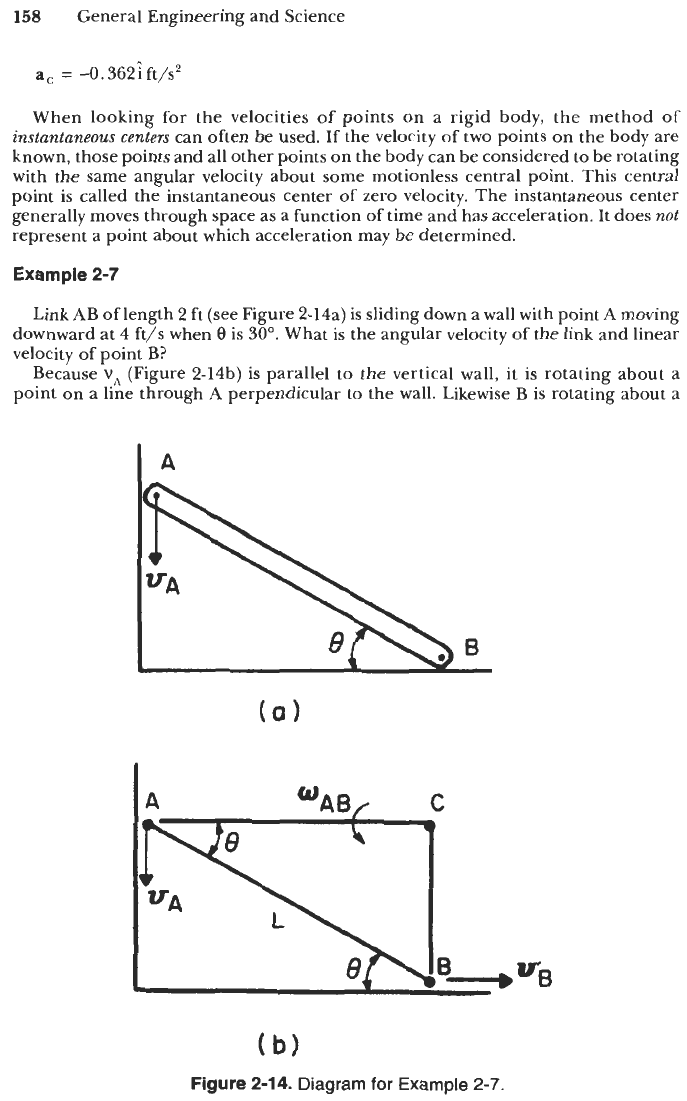
Example
2-7
Link AB of length
2
ft (see Figure 2-14a) is sliding down
a
wall with point
A
moving
downward at 4 ft/s when
0
is 30". What is the angular velocity of the link and linear
velocity of point
B?
Because
v,
(Figure 2-14b) is parallel to the vertical wall,
it
is rotating about a
point on a line through A perpendicular to the wall. Likewise
B
is rotating about a
(b)
Figure
2-1
4.
Diagram for Example
2-7.

Dynamics
159
point on a line through
B
perpendicular to
v,.
These two lines intersect at
C,
the
instantaneous center.
AC
=
L
cos
e
=
z
x
0.866
=
1.73
ft
w,,
=
-
AC
1.73ft
where
wAB
=
2.31 rad/s
=
the angular velocity of the link and of any line on the link
Iv,I
=
2.31ft/s
Kinetics
In
kinetics,
Newton's second law, the principles of kinematics, conservation of
momentum, and the laws of conservation of energy and mass are used to develop
relationships between the forces acting on a body or system of bodies and the result-
ing motion.
Applications
of
Newton's Second Law.
Problems involving no unbalanced couples
can often be solved with the second law and the principles of kinematics.
As
in statics,
it is appropriate to start with a free-body diagram showing all forces, decompose the
forces into their components along a convenient set of orthogonal coordinate axes,
and then solve a set of algebraic equations in each coordinate direction.
If
the
accelerations are known, the solution
will
be for an unknown force or forces, and
if
the forces are known the solution will be for an unknown acceleration or accelerations.
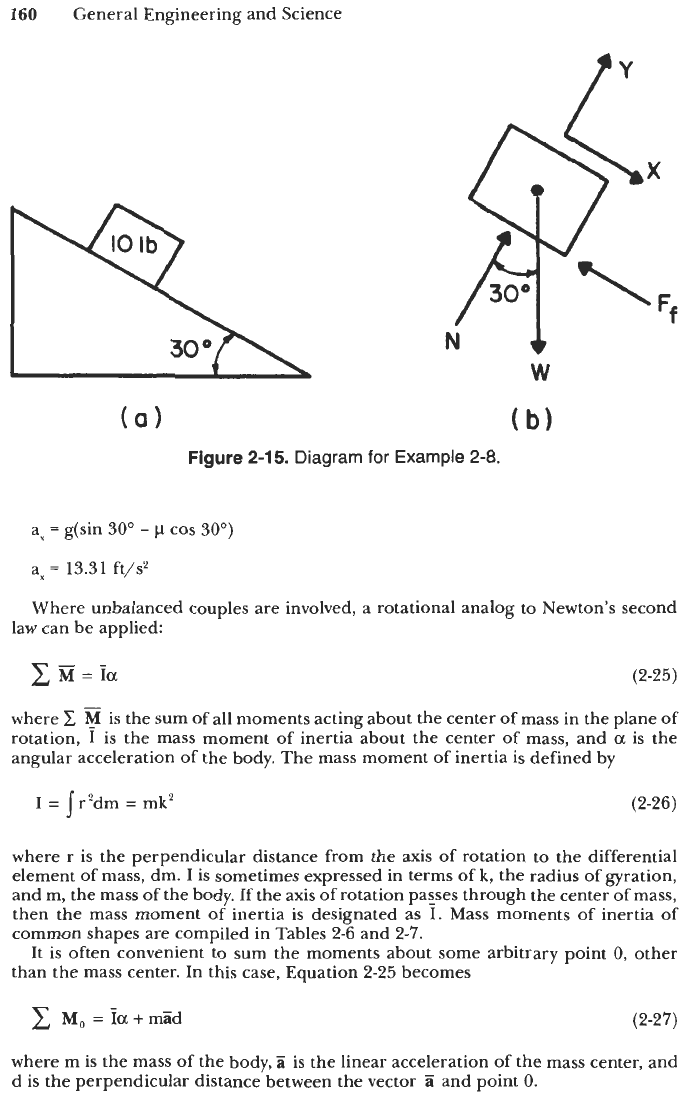
Example
2-8
In Figure 2-15a, a 10-lb block slides down a ramp inclined at an angle of 30".
If
the
coefficient of kinetic friction between the block and the ramp
is
0.1, what
will
be the
acceleration of the block?
As
shown in the free-body diagram
of
Figure 2-15b, all the motion of the block
is
parallel to the surface of the ramp; thus there is a static force balance in they direction.
Fy
=
N
-
W cos 30"
=
0
N
=
W
cos 30"
+
F,=
pN
=
pW cos 30"
Also, by Newton's second law, the force in the
x
direction produces an acceleration ax:
W
g
Fx
=
W~in30O-F~ =ma, =-a,
160
General Engineering and Science
(a)
W
Figure
2-1
5.
Diagram for Example
2-8.
ax
=
g(sin
30"
-
p
cos
30")
ax
=
13.31
ft/s'
Where unbalanced couples are involved, a rotational analog to Newton's second
law can be applied:
(2-25)
where
M
is
the sum of all moments acting about the center of mass in the plane
of
rotation, I is the mass moment
of
inertia about the center of mass, and
a
is the
angular acceleration
of
the body. The mass moment of inertia is defined by
I
=
r2dm
=
mk2
(2-26)
where r is the perpendicular distance from the axis of rotation to the differential
element of mass, dm. I
is
sometimes expressed in terms of
k,
the radius
of
gyration,
and m, the mass of the body. If the axis of rotation pas_ses through the center of mass,
then the mass moment
of
inertia is designated as
I.
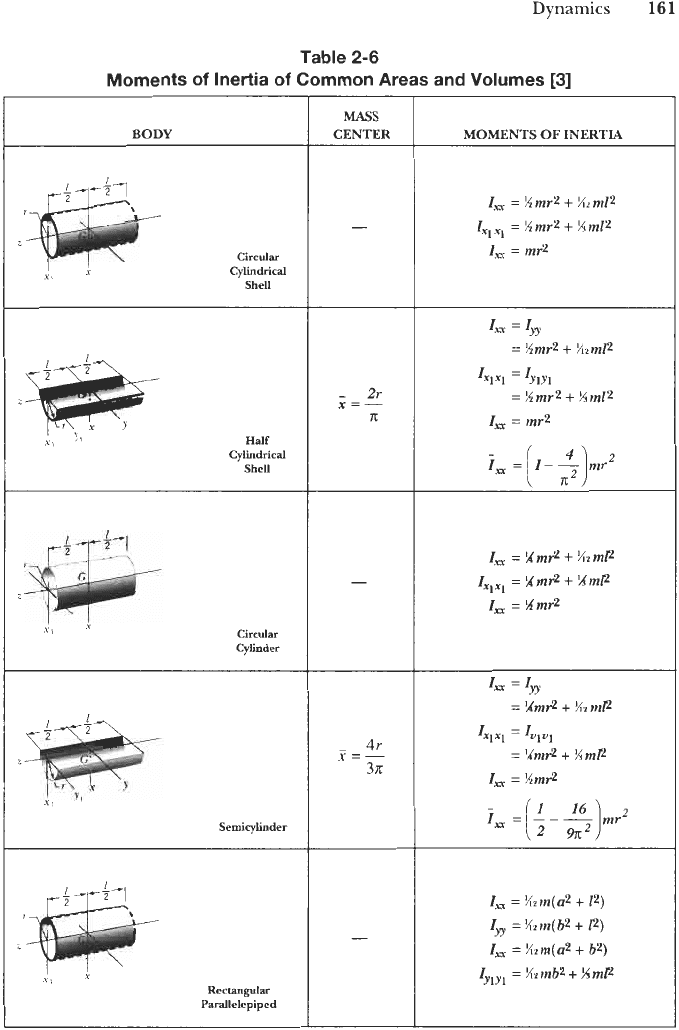
Mass moments of inertia of
common shapes are compiled in Tables
2-6
and
2-7.
It is often convenient to sum the moments about some arbitrary point
0,
other
than the mass center. In this case, Equation
2-25
becomes
C
M,
=h+m?id
(2-27)
where m is the mass of the body,
?i
is the linear acceleration of the mass center, and
d is the perpendicular distance between the vector
ii
and point
0.
Dynamics
161
Table
2-6
Moments of Inertia
of
Common Areas and Volumes
[3]
BODY
Circular
Shell
XI
I'
'
Cylindrical
Half
Cylindrical
Shell
Circular
Cylinder
x>
"
Semicylinder
I'
x,
'
Rectangular
Parallelepiped
MASS
CENTER
-
4r
3n
x=-
MOMENTS
OF
INERTIA
I,
=
Ym9
i
KP
mP
Ixlxl
=
Ym9
i
XmP
la
=
Xm19
I,
=
Iw
IXIXl
=
IUIUl
=
Ym3
+
KzmP
=
Ym9
+
MmP
I,
=
Xm9
I,
=
Knm(a2
+
12)
In
=
Knm(b2
+
12)
I,
=
Knm(a2
+
b2)
IYln
=
Knmb2
+
MmP

162
General Engineering and Science
FIGURE
\
Arc
Segment
\
Quarter
and
Semicirmlar Arcs
T”’
y-a---
Y
I
TriangularArea
I
-
Lb-’
xo
Rectangular
Area
+
__
IY
I
Quarter
Circular
Area
-
4L.c
Table
2-7
SOURCE:
Meriam
pp.
498-499.
CENTROID
-
rsina
r=-
a
-
a+b
xx-
3
-h
Y
=3
AREA
MOMENTS
OF
INERTIA
bh’
I
=-
I
1.2
-
bh3
I
=-
36
bh’
I
=-
‘I
4
bh’
I
=-
x3
-
bh3
I
=-
=
12
-
bh
J=
-
(bz
+
hz)
12
r4
1
.
I,
=-(a
--sin
2a)
42
r‘
1
,
I,
=-((a+-sin2a)
42
1
J=-r4a
2

Dynamics
163
If
0
is
a fixed axis or the instantaneous center of zero velocity, then Equation
2-27
reduces to
(2-28)
where
I,,
is
the mass moment of inertia about point
0.
I,,
may be found from Equation
2-26,
or
it
may be calculated from the parallel axis theorem
I,>
=
I
+
ml-'
(2-29)
where
f
is the distance from
0
to the center of mass. The parallel axis theorem may
be used to find I,, regardless of whether I,, is a fixed axis
of
instantaneous center of
zero velocity.
Example
2-9
In Figure
2-16
a
10
lb cylinder with a 3-in. radius rolls down a
30"
incline. What is
its angular acceleration and the linear acceleration of its center
of
mass? In the free-
body diagram of Figure
2-16,
the point
of
contact between the wheel and the ramp is
the instantaneous center
of
zero velocity. Thus,
Mi,
=
rw sin
30"
=
I,,a
rw sin
50"
a=
I,,
W
(b)
Figure
2-16.
Diagram
for
Example
2-9.

164
General Engineering and Science
From Tables 2-6 and 2-7 and the parallel
axis
theorem,
2g sin 30'
3r
a=
=
3.57rps2
ax
=
ra
=
10.73 ft/s2
Conservation of Momentum.
If the mass of a body or system of bodies remains
constant, then Newton's second law can be interpreted as a balance between force
and the time rate of change of momentum,
momentum
being a vector quantity defined
as the product of the velocity of a body and its mass.
d
d
dt
dt
F
=
ma
=
-mv
=
-G
(2-30)
Integrating Equation 2-30 with respect to time yields the impulse/momentum
equation
JFdt
=
AG
(2-31)
where Fdt is called the impulse, and
AG
is the change in momentum. Equation 2-31
can be applied explicitly and is particularly useful when the force is known as a function
of
time.
In collisions between two bodies the contact force and the duration of contact
are usually unknown. However, the duration of contact is the same for both bodies,
and the force on the first body
is
the negative of the force on the second body.
Thus the net change in momentum is zero. This is called the principle of
conservation
of
momentum.
If a collision is purely plastic, then the two colliding bodies will adhere to each
other and move on as a single body. Knowing the initial velocities and masses thus
allows calculation of the final velocity.
mlvl
+
m2v2
=
(m,
+
m,)v
(2-32)
If the collision is purely elastic or elasto-plastic, then the two bodies will depart the
collision with different velocities.
m,v,,
+
m2v21
=
m,v,2
+
m2v22
(2-33)
In this case, an additional equation is required before the final velocities may be
found. Thus, the coefficient
of
restitution e is defined as the ratio of the velocity
of
separation to the velocity of approach:
(2-34)
