Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Basic Mechanics (Statics and Dynamics)
145
t'
t
L
3
(C
1
Figure
2-4.
Diagram
for
Example
2-3.
Letting the center
of
the bottom
of
the handle be the origin, the centroid
of
Section
1,
the handle, can be found by inspection as
-
x,
=
0
rc
w,
=
-dd'Lly
=
1.33
lb
4
In Section
2,
the integral formula,
2-7,
is
applied
-
x2
=
0
where a
=
L,
-
(r
-
L,)
b
=
L,
+
L,%

146
General Engineering and Science
Transforming the integral to polar coordinates as shown in Figure 2-4:
dW,
=
L,@r cos 8dy
y
=
r sin
0
dy
=
r
COS
ede
=
14.5"= 0.253 rad
8,
=
90"
=
3
rad
2
cos
=
0.968
rad
sin
8
COS
8
de
2L,yr3
W,
7,
=
L,
-(r
-
L,)+-
6.85
y,
=
5.5+-
WZ
W,
=
6.09
lb
Substituting W, into the equation for
7,
y2
=
6.62
in.
For the entire body
x=o
-
y,W, +y2W2
=
3x1.33+6.62x6.09
y=
W,
+
W,
1.33
+
6.09
7
=
5.97 in.
When two bodies are in contact and there is a tendency for them to slide with
respect to each other, a tangential
friction
force is developed that opposes the motion.
For dry surfaces this is called
dry friction
or
coulomb
friction.
For lubricated surfaces
the friction force is called
fluidfriction,
and it is treated in the study of fluid mechanics.
Consider a block of weight
W
resting on a flat surface as shown in Figure
2-5.
The
weight of the block is balanced by a normal force
N
that is equal and opposite to the
body force. Now, if some sufficiently small sidewise force
P
is applied (Figure 2-5b) it
will be opposed by a friction force
F
that is equal and opposite to
P
and the block will
remain fixed.
If
P
is increased,
F
will simultaneously increase at the same rate until

W
Basic Mechanics (Statics and Dynamics)
147
W
N
(a
1
1
Figure
2-5. Dry
friction force.
the maximum value of the static friction force is reached, at which point the block
will
begin
to
slide.
The maximum value of the static friction force is proportional to the normal
force as
F,
=
psN
(2-12)
where
ps
is
called the
coefficient of static friction.
Once the block begins to slide, the
friction force decreases slightly and remains at a constant value defined by
F,
=
kL,N
(2-13)
where
pK
is
the
coefficient
of
kinetic friction.
The magnitude of the friction force as
a
function of the applied force
P
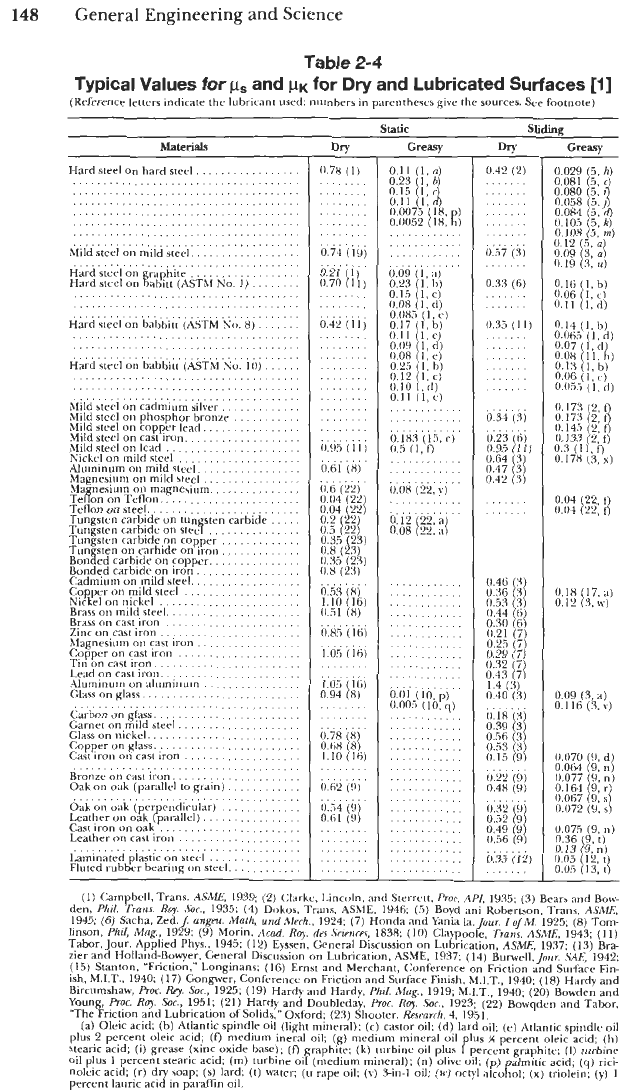
is illustrated in Figure 2-5c, and typical values for
ps
and
F~
are given for both dry and lubricated surfaces in Table 2-4.
It is often necessary to compute the forces in
structures
made up
of
connected rigid
bodies.
A
free-body diagram of the entire structure is used to develop an equation
or
equations of equilibrium based on the body weight of the structure and the external
forces. Then the structure is decomposed into its elements and equilibrium equations
are written for each element, taking advantage
of
the fact that
by
Newton’s third law
the forces between two members at
a
common frictionlessjoint are equal and opposite.
y
:a]
t.0'0
T
zz
P0.0
.........
...
('(
'55)
go'c!
.......
.........
..........
pais
uo
Buiipaq
iaqqni
painlj
pais
uo
qsqd paieu!ure'l
............
.................................
............
UOI!
ISEJ
uo
iaqieal
ye0
uo
UOl!
1se3
[lvmd yeo
un
Jaqieal
(UIPI~
01
[a[lemd)
qeo
uo
ye0
UOJ!
~SYJ
uo azuoig
UOll
ise,
(1"
UOJ!
1sy)
ssel8
un laddo3
layJ!U
uo
sse13
.....
' '
'
(nlnxpuabrad)
7eo
uo
~rg
.............................
.........
............
..........................
................
.....................
.................
................
1331s
PI!"
UO
IaUJEt)
SSP18
"0
UOqJEn
..................
................................
................
' '
'sse[B
uo
ssel3
...........
urnu!uinle uo uinu!mnw
.
'UOJ!
ire,
uo pea7
UOll
lNJ
uo
U!J
uoii
ism
uo laddo3
UOJ!
ism
uo mn!sau8ew
' '
U"l!
1-2
uo ,U!Z
.................
pais
p[!m uo
sseq
'
'
'
'laan
p~!w
uo
wn!mpe3
uoi! uo
apqm
papuog
laddo, uo Jp!qJeJ
pa
uog
.
laddo,
uo
ap!qreJ
uais8unJ
....
apqm
uas uni
uo
ap!qie>
uais8un~
' '
'palp
uo
uoua~
uovq
uo
uo
aL
......
.
.
la'ais
P~UJ
uo umisau%w
..........
pais
p1!m
uo
runuimnnf
pais pi!"
uo
iayJ!.v
................
UOJI
ISEJ
UO
[J31S
pl!E
'
'
'peal
raado,
uo
pais
ppw
'
'
aruorq Joqdsoqd
[IO
[aais
p[!w
'
ra,q!s
urnimpe~
uo
pic
pI!w
...............
......................
.................
...........
...........
..................
UOJ!
ISE3
UO
SsElg
'
[a)IJ!U
UO
[aTJ!N
.............
.............
pais
p~!m
uo
laddo3
...........
............
...........
.......
.
'
11011
uo
ap!qie>
uo
ua&J
..............
p,
uo
ap!qJe= uais8unJ
............
wnirau8eur
uo
umwauh'eE
..........
................
.....................
..................
..................
pP.21
UO
[JalS
p[!N
.........
.......
...........
..................................
.................................
.............................
:
:
;
.
:
:
!?I
'??,
WLSV!
!!!9q'q,
yo.laJts,
PfeH
.......
'8:(,)$,
WLSV)
>l!qqeq
yo
laa?s,
PyH
...............................
..............................
....
................................
..................................
' '
'
' '
(1 .ON
NLSV)
ll!qe
UO
[JalE
pS2H
..............
ai!qdu?i uo
pais
p1eH
laas
p[im uo
pais
p[!w
........................
............................
..............
pais
pieq
uo
pais
PJFH

Dynamics
149
One
of
the simplest structures is the
truss. A
truss consists of straight members
connected at their end points only. All loads, including the weight
of
the members
themselves, are considered to be supported at the joints. Due to its construction and
the assumption of loading atjoints only, the members of a truss support only loads of
axial tension or axial compression.
A rigid truss
or a rigid structure
will
not collapse
and can only deform if its members deform.
A simple truss
is
one that can be
constructed, starting with three members arranged in a triangle, by adding new
members in pairs, first connecting one end of each together to form a new joint, and
then connecting the other ends at separate existing joints of the truss.
Aframe
is a structure with at least one member that supports more than two forces.
Members of a frame may support lateral as well as axial forces. Connections in a
frame need not be located at the ends of the members. Frames, like trusses, are
designed to support loads, and are usually motionless.
A
machine
also has multiforce
members. It is designed to modify and transmit forces and, though
it
may sometimes
be stationary, it always includes parts that move during some phase of operation.
Not all structures can be fully analyzed by the methods of statics.
If
the number of
discrete equilibrium equations is equal to the number of unknown loads, then the
structure is said
to
be
statically determinate
and rigid. If there are more unknowns
than equations, then the structure is
statically indeterminate.
If
there are more equations
than unknowns, then the structure is said to be
statically indeterminate and nonrigid.
For further information on this subject, refer to References
1
and
2.
DYNAMICS
Dynamics is the study of the mechanics
of
rigid bodies in motion. It is usually
subdivided into
kinematics,
the study of the motion
of
bodies without reference to the
forces causing that motion or to the mass
of
bodies, and
kinetics,
the study
of
the
relationship between the forces acting on a body, the mass and geometry of the body,
and the resulting motion of the body.
Kinematics
Kinematics
is
based on one-dimensional differential equations of motion. Suppose
a particle is moving along a straight line, and its distance from some reference point
is
S
(see Figure 2-6a). Then its linear velocity and linear acceleration are defined by
the differential equations given in the top half of Column
1,
Table
2-5.
The solutions
Figure
2-6.
Diagrams
of
motion: (a) one-dimensional linear;
(b)
rotational.

150
General Engineering and Science
Table
2-5
One-dimensional Differential Equations
of
Motion and Their Solutions
Diffacluial
buations
a/a
=
coa~tant
a
=
a([);
a
=
a(t)
a=
~v):
a=
NO)
a=
a(s);
a=
40)
Linear
Rotafional
o=dB
y=q+at
Or
=
0,
+
1;
w
(t)
dt
'=[a
to these equations are in Columns
2-5,
for the cases
of
constant acceleration,
acceleration as a function of time, acceleration as a function of velocity, and
acceleration as a function of displacement
s.
For rotational motion, as illustrated in Figure
2-6b,
a completely analogous set of
equations and solutions are given in the bottom half of Table
2-5.
There
w
is called
the angular velocity and has units of radians/s, and
a
is called angular acceleration
and has units of radians/s2.
The equations of Table
2-5
are all scalar equations representing discrete components
of motions along orthogonal axes. The axis along which the component
w
or
a
acts
is
defined in the same fashion as for a couple. That is, the direction of
w
is outwardly
perpendicular to the plane of counterclockwise rotation (Figure
2-7).
The equations of'rable
2-5
can be used to define orthogonal components of motion
in space, and these components are then combined vectorally to give the complete
motion of the particle or point in question.
The calculation and combination of the components
of
particle motion requires
imposition of a coordinate system. Perhaps the most SomrnoQ is the Cartesian system
illustrated in Figure
2-8.
Defining unit vectors
i,
j,
and
k
along the coordinate
axes x,
y,
and
z,
the position of some point in space,
P,
can be defined by
a
position
vector,
rp:
Figure
2-7.
Wx
is a vector
of
magnitude
Wx
acting along the x axis.

Dynamics
151
P//
'
I
1
Figure
2-8.
Equations
of
motion in a Cartesian coordinate system.
A*
rp
=
xpi
+
y,j
+
z,k
(2-14)
In Equation
2-14,
x,
y, and
z
represent the coordinates
of
point
P.
The velocity
of
P
is
the vector sum
of
the component velocities:
*..
v,
=
v,i
+
v,
j
+
vzk
(2-15)
Likewise, the acceleration
of
P
is
the vector sum
of
the components
of
the accelera-
tions where
-
dv,
-
dv, a,
=
-
dv\
and a,
-
-
a,
-
-
dt
'
dt
dt
'
(2-16)
A*
ap
=
axi
+
a,
j
+
a,k
For any vector, the magnitude is the square root
of
the sum
of
the squares
of
the
components. Thus the magnitude
of
the velocity
of
point
P
would be

152
General Engineering and Science
(2-17)
The angle between the total velocity (or any other vector) and any particular
coordinate axis can be calculated from the scalar product of said vector and the unit
vector along that axis. The scalar product is defined as
a
b
=
a,b,
.t
a,b,
+
a,b,
=
lallblcos0
where
8
is the angle between vectors
a
and
b.
Thus the angle between the velocity
and the x axis is
e,
=
cos-l[
$)
(2-18)
If the magnitude and direction
of
a vector are known, its components are the
products of the magnitude and the respective direction cosines. In the case of the
velocity vector, for example, the components are
vy
=
Ivplcosey
I
PI
vZ
=
v
cosez
(2-19)
Example
2-4
A
projectile is fired at an angle of
30"
to the surface of the earth with an initial
velocity
of
1,000
ft/s
(see Figure 2-9). What
will
be its velocity and the angle of its
trajectory as a function of time?
Figure
2-9.
Diagram
for
Example 2-4.

Dynamics
153
x
Component:
The initial velocity in the
x
direction is
vx
=
866 ft/s
Assuming no air friction, this velocity is constant.
y
Component:
The initial velocity in the
y
direction is
v~<>
=
500
ft/s
In the
y
direction, the projectile has a constant acceleration
of
-g
=
-32.2 ft/sec:'.
Thus by Equation 2-2, Column,
2,
Table 2-5, its velocity as a function
of
time is
vv(t)
=
v,~]
+
at
=
v,,
-gt
32.2 ft
S2
=
500
ft/S
-
-
and the total velocity vector is
v
=
8661+(500-32.2t)j
The angle of the trajectory is found from Equation 2-18 as
866
1
[866* +(500-32.2t)']05~
ex
=
cos-'
It is often convenient to use some other coordinate system besides the Cartesian
system. In the normal/tangential system (Figure 2-10), the point
of
reference is not
fixed in space
but
is located on the particle and moves as the particle moves. There is
no position vector and the velocity and acceleration vectors are written in terms
of
n
PATH
OF
MOTION
Figure
2-10.
Normal and tangential unit vectors at different points on a path.

154
General Engineering and Science
unit vectors
.Z,
tangent to the path of motion, and
fi,
inwardly perpendicular to the
path of motion.
The velocity
is
always tangent to the path of motion, and thus the velocity vector
has only one component (Equation
2-20).
v
=
vz
(2-20)
The acceleration vector has a component tangent to the path at
=
d
IV
l/dt, which is
the rate at which the magnitude
of
the velocity vector is changing, and a component
perpendicular to the path an
=
I
v
I
z/p,
which represents the rate at which the direction
of motion is changing (Equation
2-21).
dlvl
A
\VI'
-
dt
P
a
=
a,Z+a,n
=
-z+-n
(2-21)
In Equation
2-21
p
is the local radius of curvature of the path. The normal
component of acceleration can also be expressed as an
=
p
I
w
I
or an
=
1
v
I I
w
I
where
o
is the angular velocity of the particle.
Example
2-5
of
50
ft at a speed of
30
ft/s. What is the magnitude
of
its total acceleration?
A
car is increasing in speed at a rate of
10
ft/s2 when it enters a curve with a radius
dlvl
a,
=
-
=
10
ft/s2
dt
la1
=
(lo2+
1S2)05
=
20.6
ft/s2
In addition to the Cartesian and normal/tangential coordinate systems, the
cylindrical (Figure
2-1
1)
and spherical (Figure
2-12)
coordinate systems are often used.
When dealing with the motions of rigid bodies or systems of rigid bodies, it is
sometimes quite difficult to directly write out the equations of motion of the point in
question as was done in Examples
2-6
and
2-7.
It is sometimes more practical to
analyze such a problem by
relative
motion.
That is, first find the motion with respect
to a nonaccelerating reference frame of some point on the body, typically the center
of mass or axis of rotation, and vectorally add to this the motion of the point in
question with respect to the reference point.
Example
2-6
Consider an arm
2
ft in length rotating in the counterclockwise direction about a
fixed axis at point A at a rate of
2
rpm (see Figure
2-13a).
Attached to the arm at
