Lyons W.C. (ed.). Standard handbook of petroleum and natural gas engineering.2001- Volume 1
Подождите немного. Документ загружается.


Directional Drilling
1085
The distance between the stations is 60 ft. Determine the dogleg severity.
Solution
Rate of change in inclination angle is
b=-=
40
-
30
0.1667O,/ft
60
Radius of curvature in vertical plane is
Horizontal departure (arc length of projection of wellbore in horizontal plane) is
Hd
=
R,
(COS
-
COS
$*)
=
363
(COS
30'
-
COS
40')
=
34.28
ft
Rate of change in hole direction is
-
0.2042Offt
a=L---
8 -8,
-
18-11
Hd 34.28
Hole curvature at the first station
is
c1
=
100
[(0.2042)2 sin4 30'
+
(0.1667)2]0.5
=
7.43'/100 ft
Hole curvature at the second station is
c2
=
100 [(0.2042)' sin4 40'
+
(0.1667)p]0.5
=
18.68°/100 ft
The average value is
Deflection
Tool
Orientation
Application
of
a deflecting tool (e.g., downhoIe motor with a bent sub)
requires determining the orientation of the tool
so
that the hole takes the desired
course. There are three effects to consider when setting a deflection tool:
1.
the existing borehole inclination angle
2.
the existing borehole direction angle
3. the bent sub angle of the deflection tool itself
These three effects in combination will result in a new dogleg of a wellbore.
The deflection tool orientation parameters can be obtained using the vectorial
method of
D.
Ragland, the Ouija Board", or the three-dimensional mathematical
deflecting model.

1086
Drilling and Well Completions
Vectorial Method of
D.
Ragland
[134]
This method is explained by solving two example problems.
Example
3
facing change from original course line angle if the data are as follows:
Existing hole inclination angle:
10"
Existing hole direction:
N30'W
Desired change of azimuth:
25"
(to the left)
Desired hole inclination:
8O
Determine the deflection tool-face orientation, tool deflection angle
and
tool
Solution
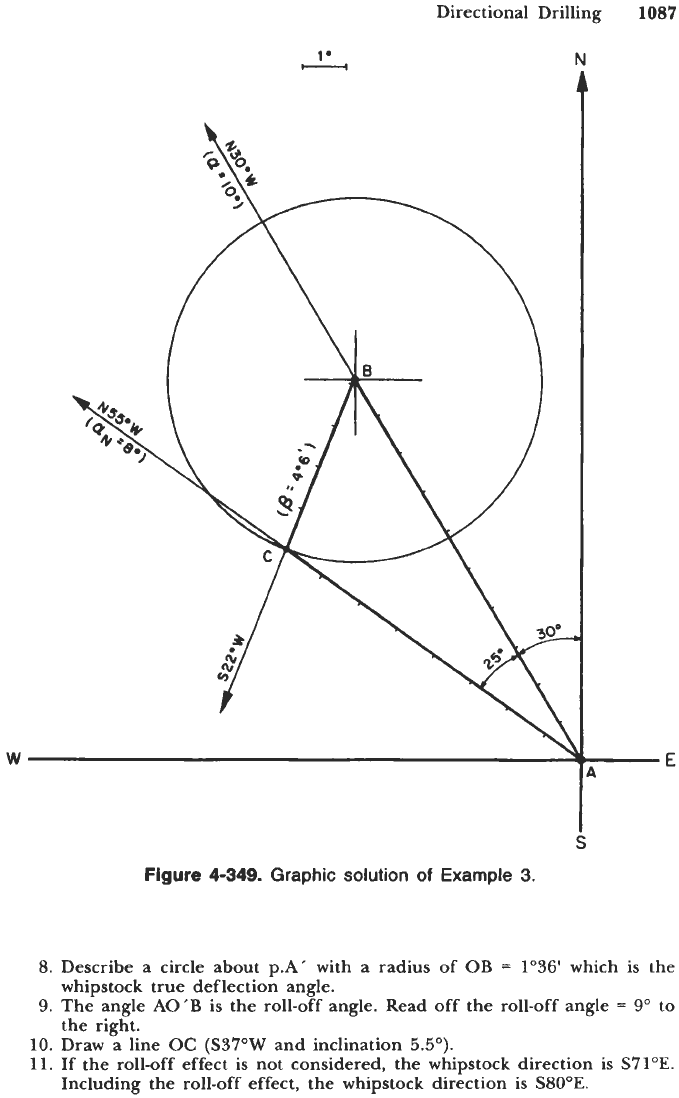
The solution to this problem is shown in Figure
4-349.
The following steps
are involved in preparing
a
Ragland diagram.
1.
Lay a quadrant
NS-W-E.
2. Select a scale
for
the angles.
3.
With a protractor lay off an angle
30'
from
N.
4.
Using the selected angle scale find p.B
(10"
from p.A).
5.
With a protractor lay off an angle
25"
to the left of line
AB.
6.
Find p.C using the angle scale
(So
from p.A).
7.
Describe
a
circle about p.B with a radius of CB
=
4'6'
(read off from the
8.
Read off required tool-face orientation: S22"W
9.
Read off required tool facing change from original course line:
131'.
diagram). This
is
the desired tool deflection angle.
Example
4
The original hole direction and inclination were measured to be
S60"W
and
6",
respectively. To obtain a new hole direction of S75'W with an inclina-
tion angle of
7',
a whipstock with the deflection angle of 2" was used and
oriented correctly.
After drilling
90
ft, a checkup measurement was performed that revealed that
the hole direction is
S72"W
and
the inclination is
6'30'.
Determine the mag-
nitude of roll-off for this system and the real deflection angle of the whipstock.
How should the whipstock be oriented to drill a hole with a direction of
S37"W
and inclination of
5.5"?
Solution
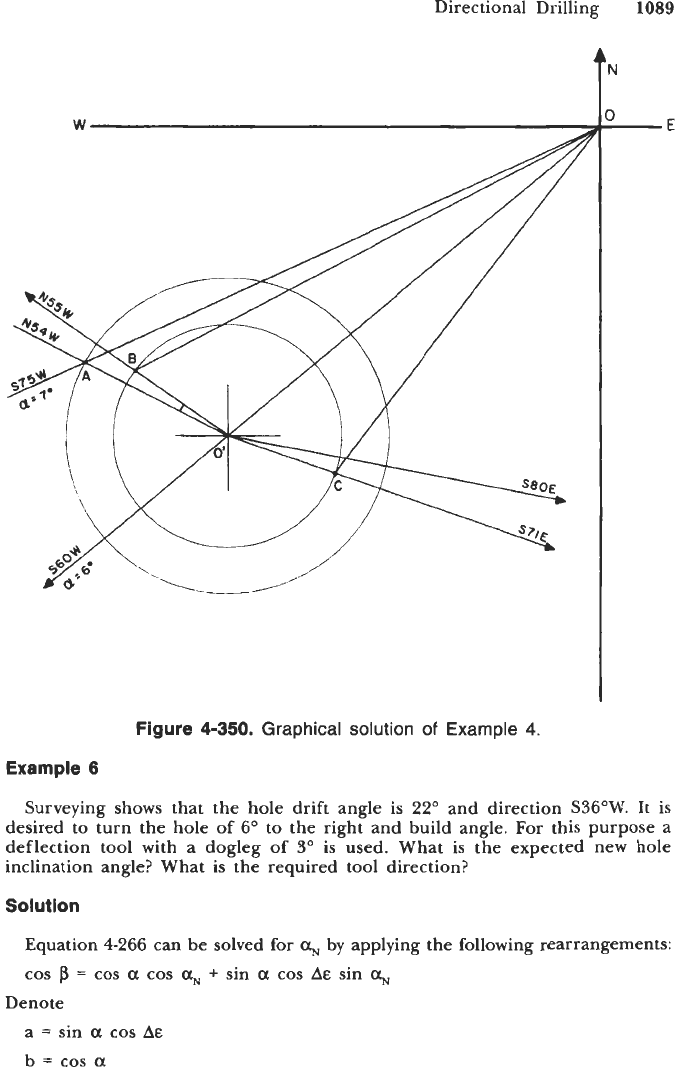
The solution to this problem is shown in Figure
4-350.
Steps
1
and
2
are the
same as in Example
3.
3.
Lay off an angle
60'
from
S.
4.
Draw a line
00'.
5.
Draw a line
OA
that will represent the desired new hole direction
6.
Read off the original whipstock orientation
N64'W.
7.
Draw a line
OB
(direction,
S72'W;
inclination,
6'30').
(S72"W).
Point
A
is found at
a
distance of 7" from point
0.
Directional Drilling
1087
1.
.
I
L
-E
A
Figure
4-349.
Graphic
solution
of Example
3.
8.
Describe a circle about p.A' with a radius of
OB
=
l"36'
which is the
9.
The angle AO'B is the roll-off angle. Read off the roll-off angle
=
9"
to
whipstock true deflection angle.
the right.
10.
Draw a line
OC
(S37"W
and inclination
5.5").
11.
If
the roll-off effect
is
not considered, the whipstock direction is
S71"E.
Including the roll-off effect, the whipstock direction is
S80"E.

1088
Drilling and Well Completions
Note:
With a Dyna-Drill downhole motor there will be a left-hand reaction
torque; therefore, the tool should be turned counterclockwise from the ideal
position.
Three-Dimensional Deflecting Model
Recently a mathematical model has been presented [135] that enables one
to
analyze and plan deflection tool runs. The model is a set of equations that relate
the original hole inclination angle
(a),
new hole inclination angle
(aN),
overall
angle change
(p),
change of direction
(Ae),
and tool-face rotation
from
original
course direction
(y).
These equations are given below:
p
=
arc cos(cos
a
cos
a,
+
sin
a
sin
a,
cos
A&)
%
=
arc cos(cos
a
cos
j3
-
sin
p
sin
a
cos
7)
(4-266)
(4-267)
I
tan
p
sin
y
sin
a
+
tan
p
cos
a
cos
y
AE
=
arc tang
(4-268)
The above equations can be rearranged to the form suitable for a solution of a
particular problem.
A
hand-held calculator may be used to perform required
calculations
[
1361.
Practical usefulness of this model is presented below.
Example
5
Original hole direction and inclination is N20"E
and
IOo,
respectively. It is
desired to deviate the borehole
so
that the new hole inclination is
13"
and
direction N30"E.
What is the tool orientation and deflecting angle (dogleg) necessary to achieve
this turn and build?
Solution
From Equation
4-266,
/3
=
arc cos(cos 10 (cos
p)
+
sin
10
(sin
p)
cos
10)
=
3.59'
The desired tool deflection angle (e.g., bent sub)
is
3.59".
Solving Equation
4-267
for
y
yields
cos1o(cos3.59)-cos13
sin 3.59 sin
10
cos
a
cos
p
-
cos
aN
y
=
arc cos
=
arc
cos
sin
p
sin
a
=
38.53'
Consequently the tool-face orientation is
20
+
38.53
=
N58.53"N
Directional Drilling
1089
L
N
OE
Figure
4-350.
Graphical solution
of
Example
4.
Example
6
Surveying shows that the hole drift angle is
22"
and direction
S36"W.
It is
desired to turn the hole of
6"
to the right and build angle. For this purpose
a
deflection tool with a dogleg
of
3'
is
used. What is the expected new hole
inclination angle? What is the required tool direction?
Solution
Equation
4-266
can be solved for
uN
by
applying the following rearrangements:
cos
p
=
cos
a
cos
a,
+
sin
a
cos
AE
sin
a,
Denote
a
=
sin
a
cos
A&
b
=
cos
a

1090
Drilling and Well Completions
Then
cos
p
=
(a2
+
b*)0.5 cos(a,
-
$)
where
a
+=arctan-
b
so
a,
=
arc
cos[
(
cos
p
)
+
+
a'
+
b2)0.5
=
1.99"
I
cos 3
(cos'
22
+
sin2
22~0s'
6)0.5
arc cos
I$=arctan( sin22cos6
)
=
21.890
cos
22
and
a,
=
23.88"
Using Equation
4-267,
the tool-face rotation is found to be 54.02". Consequently
the required tool direction is
N90"W.
SELECTION
OF
DRILLING PRACTICES
Factors Affecting Drilling
Rates
The factors that influence the rate of penetration during a conventional rotary
drilling process are numerous. In general these factors can be classified into
five groups.
1.
Formation mechanical and physical properties (strength, hardness, abrasive-
2. Rock bit type (tooth shape, journal angle, cone offset, fluid circulation
3. Drilling fluid type and properties (density, viscosity, fluid loss, etc., solids
4.
Drilling parameters (weight on bit, rotary speed, nozzle size, flowrate)
5.
Rig type and performance of drilling personnel (rig size, degree
of
auto-
ness, porosity, permeability, etc.)
system)
content, differential pressure, etc.)
mation, power equipment, etc.)
The detailed
and
rigorous analysis of the relationship between the drilling
rate and the aforementioned factors
is
not available as of today.

Selection
of
Drilling Practices
1091
Selection
of
Weight
on
Bit, Rotary Speed
and Drilling
Time
(Bit
Rotating Time)
To
select properly the weight on bit
W
(lb), rotary speed
N
(rpm) and bit
rotating time T, (hr), a drilling engineer should choose a criterion for selection
and a drilling model.
As
criteria for the drilling process evaluation and the
drilling parameters selection the following functions are generally used.
Drilling cost per foot C, ($/ft) is
Run cycle speed RCS (ft/hr)
is
Footage
F
(ft)
is
F
=
ROP
x
T,
(4-269)
(4-270)
(4-271)
where
Cr
=
hourly
rig cost
in
$/hr
C,
=
bit cost in
$
T,
=
trip time (nonrotating time) in hr
ROP
=
an average rate of penetration in ft/hr
The drilling model presented here is a simplified and modified model developed
by Bourgoyne and Young
[137].
The model includes three equations.
Instantaneous drilling rate equation
dF
1
-=KI,-
dt 1+Ch
where
Rate
of
bit tooth wear equation
(4-272)
dh
1
1
dt
A,
1+H,h
-=-I,-
where

1094
Drilling and Well Completions
(4-273)
Rate of bit bearing wear equation is
dB1
dt
S
-=-I,
(4-274)
where
where
F
=
footage in
ft
t
=
bit rotating time in hr
W
=weight on bit in
lo5
lb
N
=
bit rotary speed in rpm
D,
5
bit diameter in in.
h
=
rock bit tooth dullness (fraction of original height worn
B
=
bearing wear (fraction of a bearing life expected),
0
I
C
=
constant dependent upon bit and formation type
A,
=
formation abrasiveness parameter in hr
K
=
formation drillability parameter in ft/hr
S
*
bit bearing parameter in hr
away),
0
I
h
I1
BI1
a1,a4
=
bit weight and rotary speed exponents
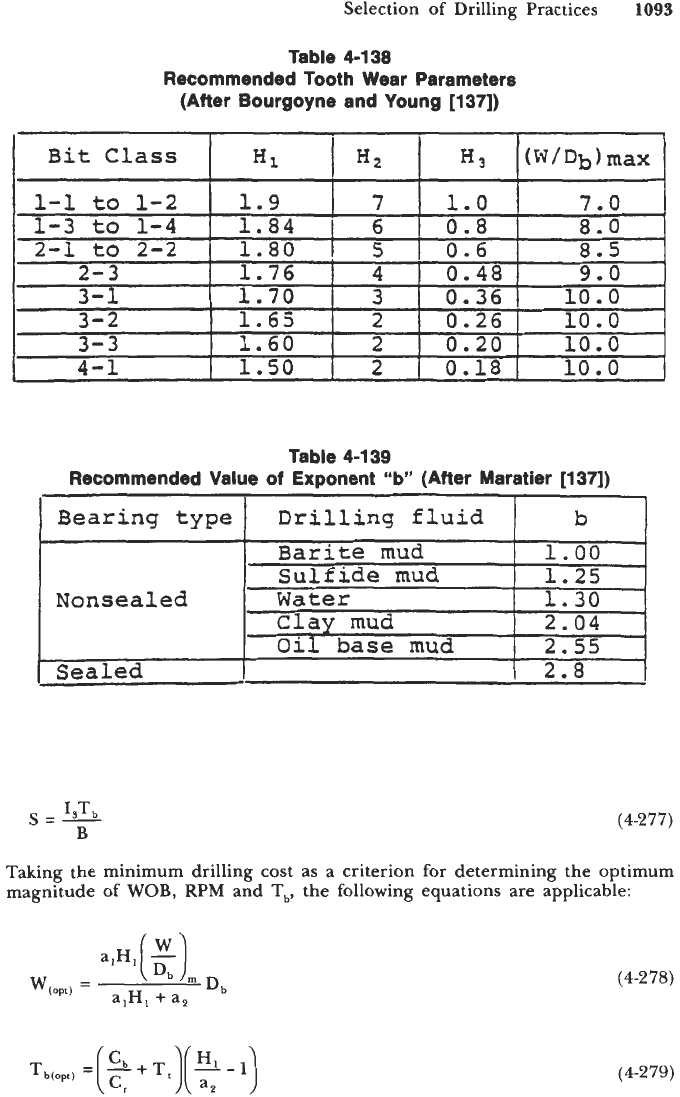
H,,H,,H,
or
(W/Db),
=
constants which depend upon bit type (see Table
4-138)
b
=
constant depending upon bearing and drilling fluid type
4
=
normalized weight on bit in
4
x
lo3
Ib
(see Table
4-139)
100
=
normalized rotary speed in rpm
Although the presented model is not a perfect simulation of the real system,
it
provides a possibility of determining the optimal
WOB,
RPM
and T,.
The formation abrasiveness, drillability and bit-bearing parameters are cal-
culated from the following formulas based on data available from previous
drilling experience.
A,
=
I*Tb
h,
+-h:
H*
2
F
Is
1
h,
+
9
In(Ch,
+
1)
(4-275)
(4-276)
Selection of Drilling Practices
1093
1-1
to 1-2
1-3
to
1-4
2-1 to 2-2
2-3
3-1
3-2
3-3
4-1
Table 4-138
Recommended Tooth Wear Parameters
(After Bourgoyne and Young [137])
1.9
7
1.0
7.0
1.84
6
0.8 8.0
1.80
5
0.6
8.5
1.76
4
0.48
9.0
1.70
3
0.36
10.0
1.65
2
0.26
10.0
10.0
1.60
2 0.20
1.50
21
0.18
10.0
Nonsealed
Sealed
Table 4-139
Recommended Value
of
Exponent “b” (After Maratier [137])
I
Bearing type
1
Drilling
fluid
1
b
Barite
mud
1.00
Sulfide
mud
1.25
Water
1.30
Clay
mud
2.04
Oil
base
mud
2.55
2.8
(4-277)
s=-
b
B
Taking the minimum drilling cost as a criterion
for
determining the optimum
magnitude
of
WOB,
RPM and
Tb,
the following equations are applicable:
(4-278)
(4-279)

1094
Drilling and Well Completions
(4-280)
Equations
4-278, 4-279
and
4-280
are valid only if the bit life is limited by tooth
wear or economical drilling rate.
Example
1
The following data are available from an offset well:
Weight on bit, W
=
45
x
lo3
lb;
Rotary speed,
N
=
130
rpm;
Footage, F
=
580
ft;
Bit rotating time, T,
=
16
hr;
Trip time, Tt
=
9
hr;
Bit diameter,
D,
=
124
in.;
Bit type: SDS;
From Table
4-138:
HI
=
1.9,
H,
=
7,
H,
=
1.0,
(W/D,)m
=
7;
Bearing type: nonsealed, clay mud;
From Table
4-139:
b
=
2.06;
Tooth wear, h,
=
2;
Bearing wear, B
=
j;
Exponents: a,
=
1.0,
a2
=
0.8;
Constant: C
=
6.5.
Find the formation abrasiveness and drillability parameters and the bit-bearing
constant.
Solution
Calculate the dimensionless functions:
I,
=
(
-
)"(
-
)"
=
(
45
)I"(
-
130)0'8
=
1.323
4D,
100 4~12.25 100
7--
12.25
