Лыков С.Н., Гасумянц В.Э., Рыков С.А. Квантовая механика. Учебное пособие
Подождите немного. Документ загружается.


Ɇɢɧɢɫɬɟɪɫɬɜɨ ɨɛɪɚɡɨɜɚɧɢɹ Ɋɨɫɫɢɣɫɤɨɣ Ɏɟɞɟɪɚɰɢɢ
ɋȺɇɄɌ-ɉȿɌȿɊȻɍɊȽɋɄɂɃ
ȽɈɋɍȾȺɊɋɌȼȿɇɇɕɃ ɉɈɅɂɌȿɏɇɂɑȿɋɄɂɃ ɍɇɂȼȿɊɋɂɌȿɌ
ɋ. ɇ. Ʌɵɤɨɜ ȼ. ɗ. Ƚɚɫɭɦɹɧɰ ɋ. Ⱥ. Ɋɵɤɨɜ
ɄȼȺɇɌɈȼȺə ɆȿɏȺɇɂɄȺ
Ɋɭɤɨɜɨɞɫɬɜɨ ɩɨ ɪɟɲɟɧɢɸ ɡɚɞɚɱ
ɑɚɫɬɶ 2
ɍɱɟɛɧɨɟ ɩɨɫɨɛɢɟ
ɋɚɧɤɬ-ɉɟɬɟɪɛɭɪɝ
ɂɡɞɚɬɟɥɶɫɬɜɨ ɋɉɛȽɉɍ
2004
ɍȾɄ 530.145 (075.8)
Ʌɵɤɨɜ ɋ.ɇ., Ƚɚɫɭɦɹɧɰ ȼ.ɗ., Ɋɵɤɨɜ ɋ.Ⱥ. Ʉɜɚɧɬɨɜɚɹ ɦɟɯɚɧɢɤɚ. Ɋɭɤɨɜɨɞɫɬɜɨ ɩɨ
ɪɟɲɟɧɢɸ ɡɚɞɚɱ. ɑ. 2: ɍɱɟɛ. ɩɨɫɨɛɢɟ. ɋɉɛ.: ɂɡɞ-ɜɨ ɋɉɛȽɉɍ, 2004. 158 ɫ.
ɉɨɫɨɛɢɟ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɝɨɫɭɞɚɪɫɬɜɟɧɧɨɦɭ ɨɛɪɚɡɨɜɚɬɟɥɶɧɨɦɭ ɫɬɚɧɞɚɪɬɭ
ɩɨɞɝɨɬɨɜɤɢ ɩɨ ɧɚɩɪɚɜɥɟɧɢɹɦ: 550700 «ɗɥɟɤɬɪɨɧɢɤɚ ɢ ɦɢɤɪɨɷɥɟɤɬɪɨɧɢɤɚ», 551900
«Ɉɩɬɨɬɟɯɧɢɤɚ», 553100 «Ɍɟɯɧɢɱɟɫɤɚɹ ɮɢɡɢɤɚ», ɩɨ ɫɩɟɰɢɚɥɶɧɨɫɬɹɦ 014100
«Ɇɢɤɪɨɷɥɟɤɬɪɨɧɢɤɚ ɢ ɩɨɥɭɩɪɨɜɨɞɧɢɤɨɜɵɟ ɩɪɢɛɨɪɵ», 200100 «Ɇɢɤɪɨɷɥɟɤɬɪɨɧɢɤɚ ɢ
ɬɜɟɪɞɨɬɟɥɶɧɚɹ
ɷɥɟɤɬɪɨɧɢɤɚ», 190700 «Ɉɩɬɢɤɨɷɥɟɤɬɪɨɧɧɵɟ ɩɪɢɛɨɪɵ ɢ ɫɢɫɬɟɦɵ»,
071400 «Ɏɢɡɢɱɟɫɤɚɹ ɷɥɟɤɬɪɨɧɢɤɚ», 071500 «Ɋɚɞɢɨɮɢɡɢɤɚ ɢ ɷɥɟɤɬɪɨɧɢɤɚ».
ɉɨ ɤɭɪɫɭ «Ʉɜɚɧɬɨɜɚɹ ɦɟɯɚɧɢɤɚ» ɢɡɞɚɧɨ ɭɱɟɛɧɨɟ ɩɨɫɨɛɢɟ ɋ. ɇ. Ʌɵɤɨɜɚ
«Ʉɜɚɧɬɨɜɚɹ ɦɟɯɚɧɢɤɚ» (ɋɉɛ.: ɂɡɞ-ɜɨ ɋɉɛȽɌɍ, 2001) ɢ ɩɟɪɜɚɹ ɱɚɫɬɶ ɪɭɤɨɜɨɞɫɬɜɚ ɩɨ
ɪɟɲɟɧɢɸ ɡɚɞɚɱ ɋ.ɇ.Ʌɵɤɨɜ, ȼ.ɗ.Ƚɚɫɭɦɹɧɰ, ɋ.Ⱥ.Ɋɵɤɨɜ «Ʉɜɚɧɬɨɜɚɹ ɦɟɯɚɧɢɤɚ.
Ɋɭɤɨɜɨɞɫɬɜɨ ɩɨ ɪɟɲɟɧɢɸ ɡɚɞɚɱ. ɑɚɫɬɶ
1» (ɋɉɛ
.: ɂɡɞ-ɜɨ ɋɉɛȽɉɍ, 2003). ɇɚɫɬɨɹɳɟɟ
ɩɨɫɨɛɢɟ ɹɜɥɹɟɬɫɹ ɜɬɨɪɨɣ ɱɚɫɬɶɸ ɞɨɩɨɥɧɟɧɢɹ ɤ ɩɟɪɜɨɦɭ ɢɡ ɩɟɪɟɱɢɫɥɟɧɧɵɯ ɩɨɫɨɛɢɣ. ȼ
ɧɟɦ ɩɪɢɜɟɞɟɧɵ ɡɚɞɚɱɢ ɫ ɪɟɲɟɧɢɹɦɢ, ɪɟɤɨɦɟɧɞɭɟɦɵɟ ɞɥɹ ɢɡɭɱɟɧɢɹ ɧɚ ɩɪɚɤɬɢɱɟɫɤɢɯ
ɡɚɧɹɬɢɹɯ ɩɨ ɤɭɪɫɭ «Ʉɜɚɧɬɨɜɚɹ ɦɟɯɚɧɢɤɚ». Ƚɥɚɜɧɨɟ ɜɧɢɦɚɧɢɟ ɭɞɟɥɟɧɨ ɮɢɡɢɱɟɫɤɢɦ
ɩɪɢɧɰɢɩɚɦ ɢ ɢɥɥɸɫɬɪɚɰɢɢ ɩɪɢɦɟɪɚɦɢ ɪɟɚɥɢɡɚɰɢɢ ɷɬɢɯ ɩɪɢɧɰɢɩɨɜ ɜ ɦɚɬɟɦɚɬɢɱɟɫɤɨɦ
ɚɩɩɚɪɚɬɟ ɤɜɚɧɬɨɜɨɣ ɬɟɨɪɢɢ. Ɂɚɞɚɱɢ ɫɝɪɭɩɩɢɪɨɜɚɧɵ ɩɨ ɬɟɦɚɦ,
ɩɪɢɱɟɦ ɢɯ ɭɪɨɜɟɧɶ
ɫɥɨɠɧɨɫɬɢ ɢ ɨɱɟɪɟɞɧɨɫɬɶ ɫɨɝɥɚɫɨɜɚɧɵ ɫ ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶɸ ɢɡɥɨɠɟɧɢɹ
ɥɟɤɰɢɨɧɧɨɝɨ ɦɚɬɟɪɢɚɥɚ.
ɉɪɟɞɧɚɡɧɚɱɟɧɨ ɞɥɹ ɫɬɭɞɟɧɬɨɜ ɢ ɚɫɩɢɪɚɧɬɨɜ, ɢɡɭɱɚɸɳɢɯ ɞɢɫɰɢɩɥɢɧɵ
«Ɍɟɨɪɟɬɢɱɟɫɤɚɹ ɮɢɡɢɤɚ», «Ɏɢɡɢɤɚ ɬɜɟɪɞɨɝɨ ɬɟɥɚ», «Ɏɢɡɢɤɚ ɩɨɥɭɩɪɨɜɨɞɧɢɤɨɜ».
ɂɥ. 14. Ȼɢɛɥɢɨɝɪ.: 12 ɧɚɡɜ.
ɉɟɱɚɬɚɟɬɫɹ ɩɨ ɪɟɲɟɧɢɸ ɪɟɞɚɤɰɢɨɧɧɨ-ɢɡɞɚɬɟɥɶɫɤɨɝɨ ɫɨɜɟɬɚ ɋɚɧɤɬ-
ɉɟɬɟɪɛɭɪɝɫɤɨɝɨ ɝɨɫɭɞɚɪɫɬɜɟɧɧɨɝɨ ɩɨɥɢɬɟɯɧɢɱɟɫɤɨɝɨ ɭɧɢɜɟɪɫɢɬɟɬɚ.
ɋɚɧɤɬ-ɉɟɬɟɪɛɭɪɝɫɤɢɣ ɝɨɫɭɞɚɪɫɬɜɟɧɧɵɣ
ɩɨɥɢɬɟɯɧɢɱɟɫɤɢɣ ɭɧɢɜɟɪɫɢɬɟɬ, 2004
ɈȽɅȺȼɅȿɇɂȿ
Ƚɥɚɜɚ 5. Ȼɚɪɶɟɪɵ. ɋɨɫɬɨɹɧɢɹ ɫ ɧɟɩɪɟɪɵɜɧɵɦ ɫɩɟɤɬɪɨɦ ɷɧɟɪɝɢɢ …………….......…3
Ɂɚɞɚɱɢ……….......………………
……………………………………………………..…3
Ɋɟɲɟɧɢɹ ………………………………………………………………………………...5
Ƚɥɚɜɚ 6. Ɂɚɞɚɱɢ ɨɛ ɨɫɰɢɥɥɹɬɨɪɚɯ ………………………………………………………..22
Ɂɚɞɚɱɢ ………………….
…
………………
…
………………………………………....23
Ɋɟɲɟɧɢɹ …………………………………………………………………………….....25
Ƚɥɚɜɚ 7. Ɇɨɦɟɧɬ ɢɦɩɭɥɶɫɚ …………
……………………………………………………..52
Ɂɚɞɚɱɢ …….
…………………………………………………………………………....56
Ɋɟɲɟɧɢɹ …………………………………………………………………………….....58
Ƚɥɚɜɚ 8.
ɋɩɢɧ ……………………………............................................................................76
Ɂɚɞɚɱɢ ………………………….
…
………
…
………………………………………....79
Ɋɟɲɟɧɢɹ …………
………
….…………………………………………………
…
….....81
Ƚɥɚɜɚ 9. ȼɨɡɦɭɳɟɧɢɟ, ɩɟɪɟɯɨɞɵ ……………………………............................................98
Ɂɚɞɚɱɢ …………...
……….…………………………………………………………....102
Ɋɟɲɟɧɢɹ ………
………..…..……………………………………………………….....105
Ȼɢɛɥɢɨɝɪɚɮɢɱɟɫɤɢɣ ɫɩɢɫɨɤ ………………………….……………………………….……155
ɋɩɢɫɨɤ ɨɩɟɱɚɬɨɤ ɢ ɢɫɩɪɚɜɥɟɧɢɣ .……
…
………………………………
…
……………..…156
Ƚɥɚɜɚ 5. ȻȺɊɖȿɊɕ. ɋɈɋɌɈəɇɂə ɋ ɇȿɉɊȿɊɕȼɇɕɆ
ɋɉȿɄɌɊɈɆ ɗɇȿɊȽɂɂ
ȼ ɞɚɧɧɨɣ ɝɥɚɜɟ ɦɵ ɩɪɨɞɨɥɠɚɟɦ ɢɡɭɱɚɬɶ ɩɪɢɦɟɪɵ ɪɟɲɟɧɢɣ ɭɪɚɜɧɟɧɢɹ
ɒɪɟɞɢɧɝɟɪɚ. Ɂɞɟɫɶ ɩɪɢɜɟɞɟɧɨ ɧɟɫɤɨɥɶɤɨ ɡɚɞɚɱ ɨɛ ɨɞɧɨɦɟɪɧɨɦ ɞɜɢɠɟɧɢɢ
ɱɚɫɬɢɰɵ ɜ ɩɨɥɟ
)(
x
U
, ɢɦɟɸɳɟɦ ɜɢɞ ɪɟɡɤɢɯ ɫɬɭɩɟɧɟɤ. Ɉɫɧɨɜɧɨɣ ɲɚɝ ɜ ɪɟɲɟɧɢɢ
ɩɨɞɨɛɧɵɯ ɡɚɞɚɱ – ɢɫɩɨɥɶɡɨɜɚɧɢɟ ɭɫɥɨɜɢɣ ɧɟɩɪɟɪɵɜɧɨɫɬɢ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɢ
ɟɟ ɩɪɨɢɡɜɨɞɧɨɣ ɩɨ ɨɛɟ ɫɬɨɪɨɧɵ ɨɬ ɬɨɱɤɢ
x
, ɜ ɤɨɬɨɪɨɣ ɩɨɬɟɧɰɢɚɥɶɧɚɹ ɷɧɟɪɝɢɹ
ɱɚɫɬɢɰɵ ɩɪɟɬɟɪɩɟɜɚɟɬ ɫɤɚɱɨɤ. Ƚɪɨɦɨɡɞɤɨɫɬɶ ɷɬɨɣ ɩɪɨɰɟɞɭɪɵ ɩɪɢ ɧɚɥɢɱɢɢ ɭ
ɩɨɬɟɧɰɢɚɥɚ ɧɟɫɤɨɥɶɤɢɯ ɫɬɭɩɟɧɟɤ ɥɟɝɤɨ ɩɪɟɨɞɨɥɟɜɚɟɬɫɹ ɫ ɩɨɦɨɳɶɸ ɬɚɤ
ɧɚɡɵɜɚɟɦɨɝɨ ɦɟɬɨɞɚ ɦɚɬɪɢɰ ɩɟɪɟɧɨɫɚ.
Ɂɚɞɚɱɢ
5.1.
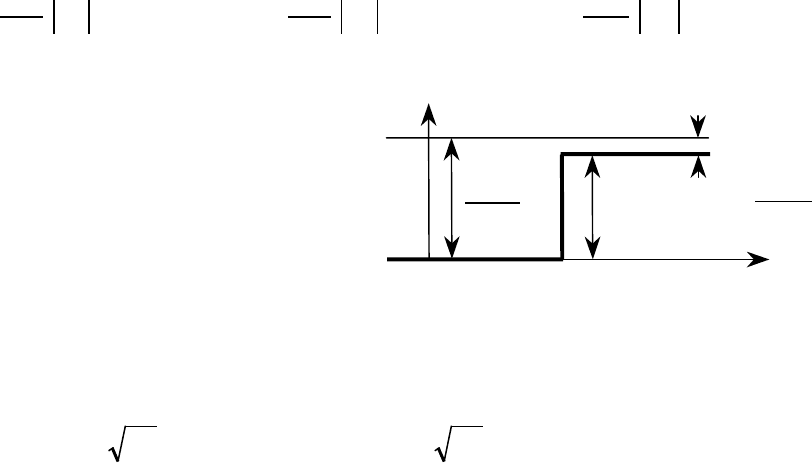
ȼɟɪɨɹɬɧɨɫɬɢ ɨɬɪɚɠɟɧɢɹ
R
ɢ ɩɪɨɯɨɠɞɟɧɢɹ ɱɚɫɬɢɰɵ, ɩɚɞɚɸɳɟɣ ɢɡ
ɨɛɥɚɫɬɢ 1 ɧɚ ɩɨɬɟɧɰɢɚɥɶɧɭɸ ɫɬɟɧɤɭ, ɢɡɨɛɪɚɠɟɧɧɭɸ ɧɚ ɪɢɫ. 5.1, ɨɩɪɟɞɟɥɹɸɬɫɹ
ɪɚɜɟɧɫɬɜɚɦɢ
D
ɩɚɞɨɬɪ
jjR / ,
ɩɚɞɩɪɨɲ
jjD / ,
ɝɞɟ
2
1
1
A
m
k
j
ɩɚɞ
=
,
2
1
1
B
m
k
j
ɨɬɪ
=
,
2
2
2
A
m
k
j
ɩɪɨɲ
=
;
n
A , – ɤɨɷɮɮɢɰɢɟɧɬɵ,
ɯɚɪɚɤɬɟɪɢɡɭɸɳɢɟ ɜ -ɨɣ ɨɛɥɚɫɬɢ
ɜɨɥɧɨɜɭɸ ɮɭɧɤɰɢɸ
n
B
n
()
x
\
ɫɬɚɰɢɨɧɚɪɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɱɚɫɬɢɰɵ ɫ
ɷɧɟɪɝɢɟɣ
mk 2/
2
1
2
= H
xki
n
xki
n
nn
eBeAx
\ )(,.2,1 n
m
k
W
2
2
2
2
=
H
)(
x
U
H
W
x
x
0
m
k
2
2
1
2
=
ɨɛɥɚɫɬɶ 1
ɨɛɥɚɫɬɶ 2
Ɋɢɫ. 5.1
ɗɬɨ ɩɨɡɜɨɥɹɟɬ ɪɚɫɫɦɚɬɪɢɜɚɬɶ
ɜɟɥɢɱɢɧɵ
xki
nnn
n
eAkxa )( ɢ
xki
nnn
n
eBkxb
)(
ɤɚɤ ɨɩɪɟɞɟɥɟɧɧɵɟ ɫ ɬɨɱɧɨɫɬɶɸ ɞɨ ɧɨɪɦɢɪɨɜɨɱɧɨɝɨ ɦɧɨɠɢɬɟɥɹ ɚɦɩɥɢɬɭɞɵ
ɜɟɪɨɹɬɧɨɫɬɢ ɞɜɢɠɟɧɢɹ ɱɚɫɬɢɰɵ ɜ -ɨɣ ɨɛɥɚɫɬɢ ɜɞɨɥɶ ɢɥɢ ɩɪɨɬɢɜ ɨɫɢn
x
,
ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ.
ɚ) Ɉɩɪɟɞɟɥɢɬɶ ɦɚɬɪɢɰɭ ɩɟɪɟɧɨɫɚ
t
ˆ
, ɫɜɹɡɵɜɚɸɳɭɸ ɡɧɚɱɟɧɢɹ
,
ɫ ,.
)(
02
xa
)(
02
xb )(
01
xa )(
01
xb
(
02
xa (
01
xa )(
02
xb
ɛ) ɇɚɣɬɢ ɦɚɬɪɢɰɭ
U
, ɫɜɹɡɵɜɚɸɳɭɸ ɢ ɫ ɢ .
ˆ
)(
01
xb ))
3
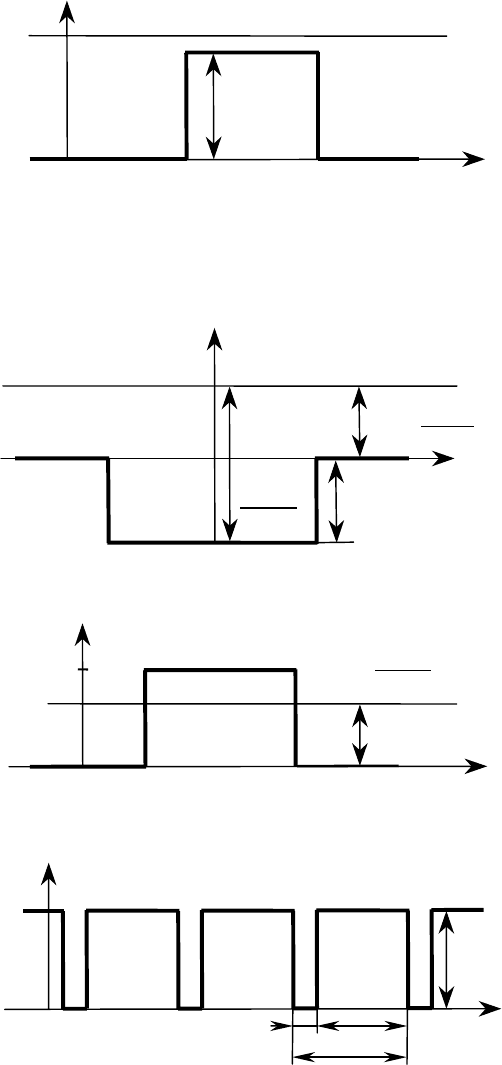
5.2. ɇɚɣɬɢ ɜɟɪɨɹɬɧɨɫɬɶ
ɩɪɨɯɨɠɞɟɧɢɹ ɢ ɜɟɪɨɹɬɧɨɫɬɶ
ɨɬɪɚɠɟɧɢɹ
D
R
ɩɪɢ ɨɞɧɨɦɟɪɧɨɦ
ɞɜɢɠɟɧɢɢ ɱɚɫɬɢɰɵ ɧɚɞ
ɩɨɬɟɧɰɢɚɥɶɧɵɦ ɛɚɪɶɟɪɨɦ
ɩɪɨɬɹɠɟɧɧɨɫɬɶɸ
d (ɪɢɫ. 5.2).
)(
x
U
H
W
x
1
x
ɨɛɥɚɫɬɶ 1 ɨɛɥɚɫɬɶ 2
x
2
ɨɛɥɚɫɬɶ 3
5.3. ɚ) ɇɚɣɬɢ ɤɨɷɮɮɢɰɢɟɧɬ
ɩɪɨɯɨɠɞɟɧɢɹ ɱɚɫɬɢɰɵ, ɫɨɜɟɪ-
ɲɚɸɳɟɣ ɨɞɧɨɦɟɪɧɨɟ ɞɜɢɠɟɧɢɟ
ɧɚɞ ɫɢɦɦɟɬɪɢɱɧɨɣ ɨɬɟɧɰɢɚɥɶɧɨɣ
ɹɦɨɣ )(
D
ɩ
x
U
, ɢ ɛɪɚɠɟɧ ɚ
ɪɢɫ. 5.3.
Ɋɢɫ. 5.2
m
k
2
2
1
2
=
H
)(
x
U
U
0
m
k
2
2
2
2
=
ax
1
x
ax
2
0
ɡɨ ɧɨɣ ɧ
ɛ) Ⱦɥɹ ɫɬɚɰɢɨɧɚɪɧɵɯ
ɫɨɫɬɨɹɧɢɣ ɱɚɫɬɢɰɵ ɜ ɭɤɚɡɚɧɧɨɦ
ɩɨɥɟ )(
x
U
, ɩɪɢɧɚɞɥɟɠɚɳɢɯ
ɧɟɩɪɟɪɵɜɧɨɣ ɱɚɫɬɢ ɷɧɟɪɝɟɬɢɱɟɫ-
ɤɨɝɨ ɫɩɟɤɬɪɚ, ɧɚɣɬɢ ɜɨɥɧɨɜɵɟ
ɮɭɧɤɰɢɢ, ɨɛɥɚɞɚɸɳɢɟ ɨɩɪɟɞɟɥɟɧ-
ɧɨɣ ɱɟɬɧɨɫɬɶɸ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ
ɩɪɟɨɛɪɚɡɨɜɚɧɢɸ
x
x
o
ɩɪɨ
ɪɚɠɟɧɧɵɣ ɧ
.
Ɋɢɫ. 5.3
)(
x
U
W
x
1
x
x
2
= x
1
+ d
123
m
k
2
2
1
2
=
H
5.4. ɇɚɣɬɢ ɤɨɷɮɮɢɰɢɟɧɬ
ɩɪɨɯɨɠɞɟɧɢɹ ɱɚɫɬɢɰɵ ɱɟɪɟɡ
ɩɨɬɟɧɰɢɚɥɶɧɵɣ ɛɚɪɶɟɪ ɬɹɠɟɧ-
ɧɨɫɬɶɸ
d , ɢɡɨɛ ɚ
ɪɢɫ. 5.4, ɩɪɢ ɭɫɥɨɜɢɢ, ɱɬɨ ɷɧɟɪɝɢɹ
ɱɚɫɬɢɰɵ
D
H
ɦɟɧɶɲɟ ɜɵɫɨɬ
ɛɚɪɶɟɪɚ
W .
Ɋɢɫ. 5.4
ɵ
5.5. ɉɨɥɭɱɢɬɶ ɭɪɚɜɧɟɧɢɟ
ɞɥɹ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɫɩɟɤɬɪɚ )(
qH
ɰɵ ɜ ɩɟɪɢɨɞɢɱɟɫɤɨɦ
ɩɨɬɟɧɰɢɚɥɟ ɫ ɩɟɪɢɨɞɨɦ ,
ɢɡɨɛɪɚɠɟɧɧɨɦ ɧɚ ɪɢɫ. 5.5.
ɍɤɚɡɚɧɢɹ. ȼɨɫɩɨɥɶɡɨɜɚɬɶɫɹ
ɩɪɟɞɫɬɚɜɥɟɧɢɟɦ ɨ ɫɨɫɬɨɹɧɢɹɯ ɫ
ɨɩɪɟɞɟɥɟɧɧɵɦ ɤɜɚɡɢɢɦɩɭɥɶɫɨɦ (ɫɦ. ɡɚɞɚɱɭ 3.8). Ɉɝɪɚɧɢɱɢɬɶɫɹ ɫɥɭɱɚɟɦ
ɱɚɫɬɢ
a
WH
,
ɝɞɟ
W – ɜɵɫɨɬɚ ɩɨɬɟɧɰɢɚɥɶɧɵɯ ɛɚɪɶɟɪɨɜ.
a=b+d
W
x
1
x
x
2
x
3
b
d
x
0
)
(
x
U
Ɋɢɫ. 5.5
5.6. ɚ) ɇɚɣɬɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ ɷɥɟɤɬɪɨɧɚ ɜ
ɨɞɧɨɪɨɞɧɨɦ ɷɥɟɤɬɪɢɱɟɫɤɨɦ ɩɨɥɟ ɩɪɢ ɨɞɧɨɦɟɪɧɨɦ ɞɜɢɠɟɧɢɢ, ɩɚɪɚɥɥɟɥɶɧɨɦ
ɧɚɩɪɚɜɥɟɧɢɸ ɩɨɥɹ.
E
4
ɛ) ɇɚɣɬɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ ɢ ɭɤɚɡɚɬɶ ɫɩɨɫɨɛ
ɜɵɱɢɫɥɟɧɢɹ ɭɪɨɜɧɟɣ ɷɧɟɪɝɢɢ ɞɥɹ ɷɥɟɤɬɪɨɧɚ ɜ «ɬɪɟɭɝɨɥɶɧɨɣ» ɛɟɫɤɨɧɟɱɧɨɣ
ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɟ:
¯
®
f
!
.0,
,0,
)(
x
xeEx
xU
Ɋɟɲɟɧɢɹ
5.1. ɚ) Ɋɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ ɒɪɟɞɢɧɝɟɪɚ ɫ ɭɤɚɡɚɧɧɵɦ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ
ɫɬɭɩɟɧɱɚɬɵɦ ɩɨɬɟɧɰɢɚɥɨɦ ɢɦɟɟɬ ɜɢɞ:
°
¯
°
®
!
\
.,
;,
)(
0
2
2
011
22
11
xxeBeA
xxeBeA
x
xkixki
xkixki
ɉɨɫɤɨɥɶɤɭ ɩɨɬɟɧɰɢɚɥ ɧɢɝɞɟ ɧɟ ɨɛɪɚɳɚɟɬɫɹ ɜ ɛɟɫɤɨɧɟɱɧɨɫɬɶ, ɬɨ ɫɚɦɚ ɜɨɥɧɨɜɚɹ
ɮɭɧɤɰɢɹ )(
x
\ ɢ ɟɟ ɩɟɪɜɚɹ ɩɪɨɢɡɜɨɞɧɚɹ ɞɨɥɠɧɵ ɧɚ ɜɫɟɣ ɨɫɢ
x
ɨɛɥɚɞɚɬɶ
ɫɜɨɣɫɬɜɨɦ ɧɟɩɪɟɪɵɜɧɨɫɬɢ. ɍɫɥɨɜɢɹ ɧɟɩɪɟɪɵɜɧɨɫɬɢ )(
x
\ ɢ )ɜ ɬɨɱɤɟ
, ɪɚɡɝɪɚɧɢɱɢɜɚɸɳɟɣ ɨɛɥɚɫɬɢ 1 ɢ 2, ɢɦɟɸɬ ɜɢɞ
(x\
c
0
xx
0101
11
xkixki
eBeA
0202
22
xkixki
eBeA
,
)(
0101
111
xkixki
eBeAik )(
0202
222
xkixki
eBeAik
. (1)
Ɉɬɫɸɞɚ ɞɥɹ ɡɧɚɱɟɧɢɣ «ɚɦɩɥɢɬɭɞ ɜɟɪɨɹɬɧɨɫɬɢ»
xki
nnn
n
eAkxa )(,
xki
nnn
n
eBkxb
)( (2)
ɜ ɬɨɱɤɟ ɩɨɥɭɱɚɟɦ
0
xx
)(
2
)(
01
12
12
02
xa
kk
kk
xa )(
2
01
12
12
xb
kk
kk
,
)(
2
)(
01
12
12
02
xa
kk
kk
xb )(
2
01
12
12
xb
kk
kk
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɬɨɱɤɟ , ɜ ɤɨɬɨɪɨɣ ɩɨɬɟɧɰɢɚɥ )
0
xx (
x
U
ɩɪɟɬɟɪɩɟɜɚɟɬ ɫɤɚɱɨɤ,
ɦɨɠɧɨ ɫɨɩɨɫɬɚɜɢɬɶ ɷɥɟɦɟɧɬɵ ɦɚɬɪɢɰɵ
jj
t
c
t
ˆ
:
)()(
011102
xatxa )(
0112
xbt ,
)()(
012102
xatxb )(
0122
xbt , (3)
5
ɝɞɟ
12
12
2211
2 kk
kk
tt
,
12
12
2112
2 kk
kk
tt
. (4)
Ɉɬɦɟɬɢɦ, ɱɬɨ ɭɤɚɡɚɧɧɚɹ ɦɚɬɪɢɰɚ
t
ˆ
ɭɧɢɦɨɞɭɥɹɪɧɚ,
1
21122211
tttt , (5)
ɚ ɨɛɪɚɬɧɚɹ ɦɚɬɪɢɰɚ ɞɚɟɬɫɹ ɡɚɦɟɧɨɣ ɜ (4) ɜɟɥɢɱɢɧ , ɧɚ ,.
1
k
2
k
2
k
1
k
ɛ) Ɏɢɡɢɱɟɫɤɚɹ ɤɚɪɬɢɧɚ ɨɬɪɚɠɟɧɢɹ ɢɥɢ ɩɪɨɯɨɠɞɟɧɢɹ ɱɚɫɬɢɰɵ ɱɟɪɟɡ
ɩɨɬɟɧɰɢɚɥɶɧɭɸ ɫɬɭɩɟɧɶɤɭ ɡɞɟɫɶ ɧɚɩɨɦɢɧɚɟɬ ɫɢɬɭɚɰɢɸ, ɪɚɫɫɦɨɬɪɟɧɧɭɸ ɜ ɡɚɞɚɱɟ
2.6. ɋ ɷɬɨɣ ɬɨɱɤɢ ɡɪɟɧɢɹ ɧɟɡɚɜɢɫɢɦɵɦɢ ɚɦɩɥɢɬɭɞɚɦɢ ɹɜɥɹɸɬɫɹ ɢ , ɚ
ɚɦɩɥɢɬɭɞɵ ɢ ɞɨɥɠɧɵ ɛɵɬɶ ɫ ɧɢɦɢ ɫɜɹɡɚɧɵ ɩɨɫɪɟɞɫɬɜɨɦ ɧɟɤɨɬɨɪɨɣ
ɭɧɢɬɚɪɧɨɣ ɦɚɬɪɢɰɵ U :
1
a
2
b
1
b
2
a
ˆ
2121111
bUaUb ,
2221212
bUaUa . (6)
ɉɟɪɟɩɢɫɚɜ ɫɨɨɬɧɨɲɟɧɢɹ (3) ɜ ɮɨɪɦɟ (6), ɧɚɯɨɞɢɦ ɫ ɭɱɟɬɨɦ (5):
222111
/ ttU ,
221222
/ ttU ,
222112
/1 tUU . (7)
ȼɟɥɢɱɢɧɚ
2
21
U
– ɷɬɨ ɤɨɷɮɮɢɰɢɟɧɬ (ɜɟɪɨɹɬɧɨɫɬɶ) ɩɪɨɯɨɠɞɟɧɢɹ ɩɪɢ
ɞɜɢɠɟɧɢɢ ɱɚɫɬɢɰɵ ɢɡ ɨɛɥɚɫɬɢ 1 ɜ ɨɛɥɚɫɬɶ 2, ɚ
D
2
12
U
– ɤɨɷɮɮɢɰɢɟɧɬ
ɩɪɨɯɨɠɞɟɧɢɹ ɩɪɢ ɩɪɨɬɢɜɨɩɨɥɨɠɧɨɦ ɧɚɩɪɚɜɥɟɧɢɢ ɞɜɢɠɟɧɢɹ. ɂɡ ɫɨɨɬɧɨɲɟɧɢɣ
(7) ɜɢɞɧɨ, ɱɬɨ ɡɧɚɱɟɧɢɟ ɧɟ ɡɚɜɢɫɢɬ ɨɬ ɧɚɩɪɚɜɥɟɧɢɹ ɩɚɞɟɧɢɹ ɱɚɫɬɢɰ ɧɚ
ɩɨɬɟɧɰɢɚɥɶɧɭɸ ɫɬɭɩɟɧɶɤɭ:
D
2
12
UD
2
22
2
21
1
t
U
. (8)
ɋ ɭɱɟɬɨɦ (4) ɧɚɯɨɞɢɦ, ɱɬɨ ɤɨɷɮɮɢɰɢɟɧɬ (ɜɟɪɨɹɬɧɨɫɬɶ) ɨɬɪɚɠɟɧɢɹ
R
ɬɚɤɠɟ ɧɟ
ɡɚɜɢɫɢɬ ɨɬ ɧɚɩɪɚɜɥɟɧɢɹ ɩɚɞɟɧɢɹ ɱɚɫɬɢɰ ɧɚ ɩɨɬɟɧɰɢɚɥɶɧɭɸ ɫɬɭɩɟɧɶɤɭ:
2
11
UR
2
2212
2
22
/ ttU
. (9)
ɉɨɞɫɬɚɜɢɜ ɜ (8), (9) ɜɵɪɚɠɟɧɢɹ ɞɥɹ ɷɥɟɦɟɧɬɨɜ
t
ˆ
-ɦɚɬɪɢɰɵ (4), ɩɨɥɭɱɚɟɦ:
6
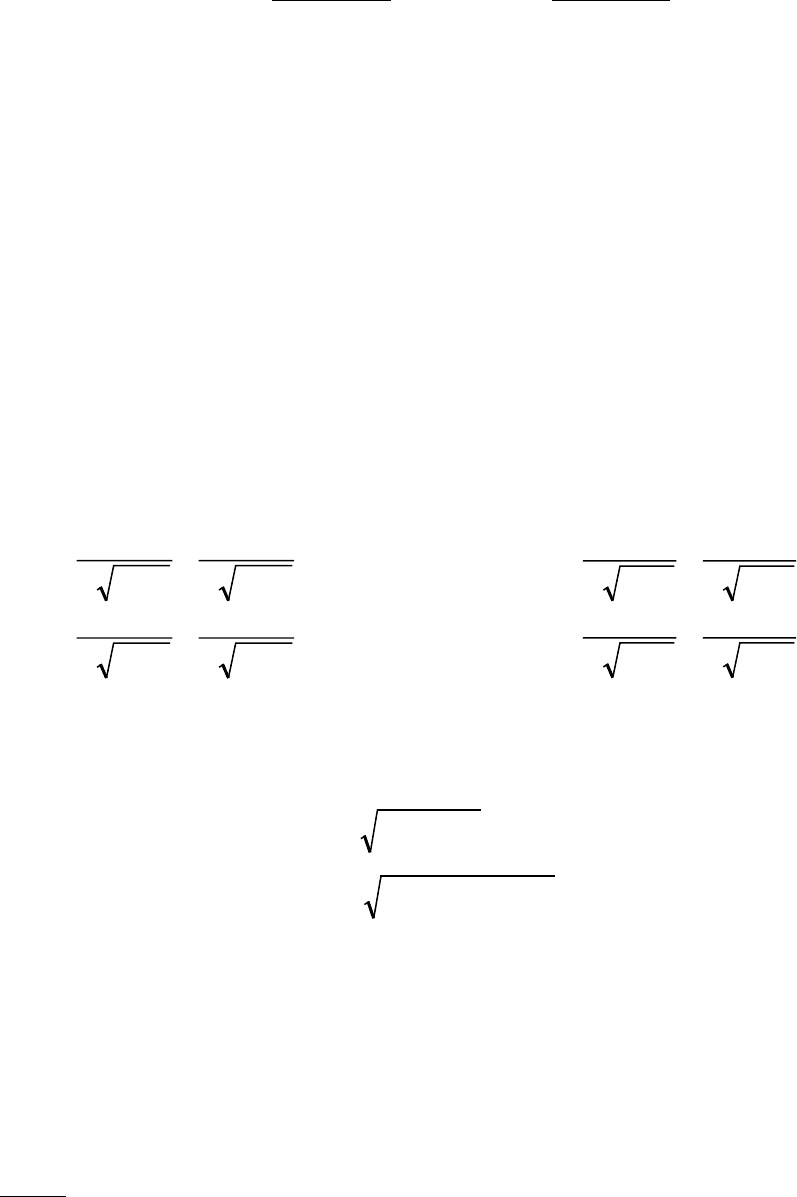
2
12
12
)(
4
kk
kk
D
,
2
12
2
12
)(
)(
kk
kk
R
. (10)
Ʉɚɤ ɢ ɞɨɥɠɧɨ ɛɵɬɶ, ɜɵɞɟɪɠɢɜɚɟɬɫɹ ɪɚɜɟɧɫɬɜɨ 1
R
D , ɩɨɞɬɜɟɪɠɞɚɸɳɟɟ
ɞɨɩɭɫɬɢɦɨɫɬɶ ɜɟɪɨɹɬɧɨɫɬɧɨɣ ɢɧɬɟɪɩɪɟɬɚɰɢɢ ɜɟɥɢɱɢɧ ɢD
R
.
5.2. ȼɨɫɩɨɥɶɡɭɟɦɫɹ ɮɨɪɦɚɥɢɡɦɨɦ ɦɚɬɪɢɰɵ ɩɟɪɟɧɨɫɚ – ɮɨɪɦɭɥɚɦɢ (2)–(9),
ɩɪɢɜɟɞɟɧɧɵɦɢ ɜ ɪɟɲɟɧɢɢ ɡɚɞɚɱɢ 5.1. Ⱦɜɢɠɟɧɢɸ ɱɚɫɬɢɰɵ ɧɚɞ ɩɨɬɟɧɰɢɚɥɶɧɵɦ
ɛɚɪɶɟɪɨɦ, ɩɨɤɚɡɚɧɧɵɦ ɧɚ ɪɢɫ. 5.2 , ɦɨɠɧɨ ɫɨɩɨɫɬɚɜɢɬɶ ɫɥɟɞɭɸɳɢɟ ɥɢɧɟɣɧɵɟ
ɫɨɨɬɧɨɲɟɧɢɹ:
)()(
111123
xatxa )(
1112
xbt ,
)()(
112123
xatxb )(
1122
xbt , (1)
ɝɞɟ – ɷɥɟɦɟɧɬɵ ɦɚɬɪɢɰɵ
jj
t
c
t
ˆ
, ɢɦɟɸɳɟɣ ɜɢɞ ɩɪɨɢɡɜɟɞɟɧɢɹ ɬɪɟɯ
ɭɧɢɦɨɞɭɥɹɪɧɵɯ ɦɚɬɪɢɰ ɢ ɜ ɫɢɥɭ ɷɬɨɝɨ ɬɚɤɠɟ ɹɜɥɹɸɳɟɣɫɹ ɭɧɢɦɨɞɭɥɹɪɧɨɣ:
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
23
23
23
23
23
23
23
23
22
22
ˆ
kk
kk
kk
kk
kk
kk
kk
kk
t
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
dik
dik
e
e
2
2
0
0
¸
¸
¸
¸
¹
·
¨
¨
¨
¨
©
§
12
12
12
12
12
12
12
12
22
22
kk
kk
kk
kk
kk
kk
kk
kk
. (2)
ȼɨɥɧɨɜɵɟ ɱɢɫɥɚ
31
kk ɢ ɨɩɪɟɞɟɥɹɸɬɫɹ ɜɟɥɢɱɢɧɨɣ
2
k H ɷɧɟɪɝɢɢ ɱɚɫɬɢɰɵ ɢ
ɜɵɫɨɬɨɣ ɩɨɬɟɧɰɢɚɥɶɧɨɝɨ ɛɚɪɶɟɪɚ W :
2
1
/2 =H mk , (3)
2
2
/)(2 =Wmk H . (4)
Ⱦɢɚɝɨɧɚɥɶɧɚɹ ɦɚɬɪɢɰɚ ɫ ɷɥɟɦɟɧɬɚɦɢ
dikxxik
ee
2122
)( rr
ɨɩɢɫɵɜɚɟɬ ɢɡɦɟɧɟɧɢɟ
ɜɟɥɢɱɢɧ ɢ )ɨɬ ɬɨɱɤɢ ɤ ɬɨɱɤɟ ɜɧɭɬɪɢ ɨɛɥɚɫɬɢ 2; ɞɜɚ ɞɪɭɝɢɯ
ɦɚɬɪɢɱɧɵɯ ɫɨɦɧɨɠɢɬɟɥɹ ɜ (2) ɨɬɜɟɱɚɸɬ ɢɡɦɟɧɟɧɢɸ ɬɚɤɢɯ ɜɟɥɢɱɢɧ ɩɪɢ
«ɩɟɪɟɧɨɫɟ» ɱɟɪɟɡ ɝɪɚɧɢɱɧɵɟ ɬɨɱɤɢ ɢ . ȼɵɱɢɫɥɢɜ ɭɤɚɡɚɧɧɨɟ ɩɪɨɢɡɜɟɞɟɧɢɟ
ɦɚɬɪɢɰ, ɩɨɥɭɱɢɦ:
)(
2
xa (
2
xb
1
x
2
x
1
x
2
x
¸
¸
¹
·
¨
¨
©
§
2
12
2
21
2
1
2
2
2
2
2
1
2
2
2
1
2
1
2
2
2
12
2
21
21
)()(),()(
)()(,)()(
4
1
ˆ
2222
2222
kkekkekkekke
kkekkekkekke
kk
t
dikdikdikdik
dikdikdikdik
. (5)
Ʉɨɷɮɮɢɰɢɟɧɬɵ ɩɪɨɯɨɠɞɟɧɢɹ ɢ ɨɬɪɚɠɟɧɢɹ
D
R
ɧɚɯɨɞɢɦ ɩɨ ɮɨɪɦɭɥɚɦ (8) ɢ (9)
7

ɡɚɞɚɱɢ 5.1:
2
2
21
2
21
21
2
22
)()(
4
1
22
kkekke
kk
t
D
dikdik
, (6)
2
2
21
2
21
2
1
2
2
2
22
12
)()(
))((
22
22
kkekke
eekk
t
t
R
dikdik
dikdik
. (7)
Ɉɤɨɧɱɚɬɟɥɶɧɵɣ ɪɟɡɭɥɶɬɚɬ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɬɚɤ:
1
2
2
2
2
2
1
22
2
2
1
sin
4
)(
1
¸
¸
¹
·
¨
¨
©
§
dk
kk
kk
D , (8)
D
R
1. (9)
Ɉɬɦɟɬɢɦ, ɱɬɨ ɞɥɹ ɰɟɥɨɱɢɫɥɟɧɧɵɯ ɡɧɚɱɟɧɢɣ ɩɚɪɚɦɟɬɪɚ S/
2
dk
ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɯɨɠɞɟɧɢɹ, ɤɚɤ ɜɢɞɧɨ ɢɡ ɮɨɪɦɭɥɵ (8), ɪɚɜɟɧ ɟɞɢɧɢɰɟ –
ɧɚɞɛɚɪɶɟɪɧɨɟ ɨɬɪɚɠɟɧɢɟ ɱɚɫɬɢɰɵ ɨɬɫɭɬɫɬɜɭɟɬ. ɇɚ ɤɚɱɟɫɬɜɟɧɧɨɦ ɭɪɨɜɧɟ ɷɬɨ
ɨɛɴɹɫɧɹɟɬɫɹ ɢɧɬɟɪɮɟɪɟɧɰɢɟɣ ɞɟɛɪɨɣɥɟɜɫɤɢɯ ɜɨɥɧ, ɨɬɪɚɠɟɧɧɵɯ ɜ ɨɞɧɭ ɢ ɬɭ ɠɟ
ɫɬɨɪɨɧɭ ɝɪɚɧɢɰɚɦɢ ɨɛɥɚɫɬɟɣ 1,2 ɢ 2,3: ɤɨɝɞɚ ɧɚ ɭɞɜɨɟɧɧɨɣ ɞɥɢɧɟ
ɩɨɬɟɧɰɢɚɥɶɧɨɝɨ ɛɚɪɶɟɪɚ ɞɟɛɪɨɣɥɟɜɫɤɚɹ ɞɥɢɧɚ ɜɨɥɧɵ ɱɚɫɬɢɰɵ
2
/2 kS O
ɭɤɥɚɞɵɜɚɟɬɫɹ ɰɟɥɨɟ ɱɢɫɥɨ ɪɚɡ, ɬɚɤɢɟ ɜɨɥɧɵ ɝɚɫɹɬ ɞɪɭɝ ɞɪɭɝɚ. ɉɪɢ ɡɚɞɚɧɧɨɣ
ɷɧɟɪɝɢɢ ɱɚɫɬɢɰɵ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɯɨɠɞɟɧɢɹ ɤɚɤ ɮɭɧɤɰɢɹ ɩɪɨɬɹɠɟɧɧɨɫɬɢ
ɛɚɪɶɟɪɚ ɩɟɪɢɨɞɢɱɟɫɤɢ ɦɟɧɹɟɬɫɹ ɨɬ ɡɧɚɱɟɧɢɹ ɞɨ
ɫ ɩɟɪɢɨɞɨɦ, ɪɚɜɧɵɦ
D
d
22
2
2
1
2
2
2
1min
)/(4 kkkkD
1
max
D 2
/
O .
5.3. ɚ) Ɉɩɪɟɞɟɥɢɜ ɜɨɥɧɨɜɵɟ ɱɢɫɥɚ ɮɨɪɦɭɥɚɦɢ
2
31
/2 =H mkk ,
2
02
/)(2 =Umk H , (1)
ɝɞɟ – ɷɧɟɪɝɢɹ ɱɚɫɬɢɰɵ, – ɝɥɭɛɢɧɚ ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɵ (ɫ ɲɢɪɢɧɨɣ
), ɦɨɠɟɦ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɨ ɜɨɫɩɨɥɶɡɨɜɚɬɶɫɹ ɪɟɡɭɥɶɬɚɬɚɦɢ (8), (9) ɡɚɞɚɱɢ
5.2:
H
0
U
ad 2
1
2
2
2
2
2
1
22
2
2
1
2sin
4
)(
1
¸
¸
¹
·
¨
¨
©
§
ak
kk
kk
D , (2)
D
R
1. (3)
ɉɪɢ ɰɟɥɨɱɢɫɥɟɧɧɵɯ ɡɧɚɱɟɧɢɹɯ ɩɚɪɚɦɟɬɪɚ
S
/2
2
ak ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɯɨɠɞɟɧɢɹ
(2) ɫɬɚɧɨɜɢɬɫɹ ɪɚɜɧɵɦ ɟɞɢɧɢɰɟ.
8

ɛ) Ɂɧɚɱɟɧɢɹ , ɩɪɢɧɚɞɥɟɠɚɳɢɟ ɨɛɥɚɫɬɢ ɧɟɩɪɟɪɵɜɧɨɝɨ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ
ɫɩɟɤɬɪɚ ɢ ɨɬɜɟɱɚɸɳɢɟ ɢɧɮɢɧɢɬɧɨɦɭ ɞɜɢɠɟɧɢɸ ɱɚɫɬɢɰɵ ɜ ɨɛɨɢɯ ɧɚɩɪɚɜɥɟɧɢɹɯ
ɨɫɢ
H
x
, ɞɜɭɤɪɚɬɧɨ ɜɵɪɨɠɞɟɧɵ [1]. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɜ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɦ ɩɪɢɦɟɪɟ
ɪɟɲɟɧɢɟ )(
x
\ ɭɪɚɜɧɟɧɢɹ ɒɪɟɞɢɧɝɟɪɚ
0)(
2
22
2
\H
\
xU
m
xd
d
=
ɫ ɩɨɬɟɧɰɢɚɥɨɦ, ɩɨɤɚɡɚɧɧɵɦ ɧɚ ɪɢɫ. 5.3., ɡɚɩɢɫɵɜɚɟɬɫɹ ɜ ɜɢɞɟ
°
¯
°
®
!
\
axeBeA
axaeBeA
axeBeA
x
xkixki
xkixki
xkixki
,
,
,
)(
33
22
11
33
22
11
. (4)
ɍɫɥɨɜɢɹ ɧɟɩɪɟɪɵɜɧɨɫɬɢ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ )(
x
\ ɢ ɟɟ ɩɪɨɢɡɜɨɞɧɨɣ )(x\
c
ɜ
ɬɨɱɤɟ ɩɪɢɜɨɞɹɬ ɤ ɥɢɧɟɣɧɨɣ ɫɜɹɡɢ ɤɨɷɮɮɢɰɢɟɧɬɨɜ , ɫ ,;ɷɬɭ
ɫɜɹɡɶ ɥɟɝɤɨ ɜɵɪɚɡɢɬɶ ɩɨɫɪɟɞɫɬɜɨɦ ɦɚɬɪɢɰɵ
1
xx
1
A
1
B
2
A
2
B
1
12
ˆ
/
tkk , ɝɞɟ
t
ˆ
– ɦɚɬɪɢɰɚ (4) ɜ
ɡɚɞɚɱɟ 5.1:
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
121121
121121
1
1
2/)(2/)(
2/)(2/)(
11
11
kkkkkk
kkkkkk
eB
eA
xki
xki
¸
¸
¹
·
¨
¨
©
§
12
12
2
2
xki
xki
eB
eA
. (5)
ɍɫɥɨɜɢɹ ɧɟɩɪɟɪɵɜɧɨɫɬɢ )(
x
\ ɢ )(x\
c
ɜ ɬɨɱɤɟ
2
xx ɚɧɚɥɨɝɢɱɧɨ ɜɟɞɭɬ ɤ
ɥɢɧɟɣɧɨɣ ɫɜɹɡɢ , ɫ ,:
3
A
3
B
2
A
2
B
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
121121
121121
3
3
2/)(2/)(
2/)(2/)(
21
21
kkkkkk
kkkkkk
eB
eA
xki
xki
¸
¸
¹
·
¨
¨
©
§
22
22
2
2
xki
xki
eB
eA
. (6)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɭɞɨɜɥɟɬɜɨɪɹɸɳɟɟ ɧɟɨɛɯɨɞɢɦɵɦ ɬɪɟɛɨɜɚɧɢɹɦ ɧɟɩɪɟɪɵɜɧɨɫɬɢ
ɪɟɲɟɧɢɟ (4) ɞɨɩɭɫɤɚɟɬ ɩɪɟɞɫɬɚɜɥɟɧɢɟ ɜ ɜɢɞɟ ɫɭɩɟɪɩɨɡɢɰɢɢ ɞɜɭɯ ɥɢɧɟɣɧɨ
ɧɟɡɚɜɢɫɢɦɵɯ ɪɟɲɟɧɢɣ ɜɢɞɚ ɢ ))(x
A
\ (x
B
\ , ɩɨɥɭɱɚɸɳɢɯɫɹ ɩɪɢ ɜɵɛɨɪɟ ɜ (4)
ɡɧɚɱɟɧɢɣ ɤɨɷɮɮɢɰɢɟɧɬɨɜ ,1
2
A 0
2
B , ɢɥɢ 0
2
A ,1
2
B , ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ:
)()()(
22
xBxAx
BA
\\ \ . (7)
ɗɬɨ ɢ ɨɡɧɚɱɚɟɬ ɧɚɥɢɱɢɟ ɞɜɭɤɪɚɬɧɨɝɨ ɜɵɪɨɠɞɟɧɢɹ ɡɧɚɱɟɧɢɣ
H
.
ɉɪɨɢɡɜɨɥɶɧɵɟ ɤɨɷɮɮɢɰɢɟɧɬɵ ɢ ɫɬɚɧɨɜɹɬɫɹ ɜɩɨɥɧɟ
ɨɩɪɟɞɟɥɟɧɧɵɦɢ, ɟɫɥɢ ɜɨɥɧɨɜɭɸ ɮɭɧɤɰɢɸ (4) ɩɨɞɱɢɧɢɬɶ ɭɫɥɨɜɢɸ ɧɨɪɦɢɪɨɜɤɢ ɢ
ɧɟɤɨɬɨɪɨɦɭ ɞɨɩɨɥɧɢɬɟɥɶɧɨɦɭ ɝɪɚɧɢɱɧɨɦɭ ɭɫɥɨɜɢɸ; ɩɨɫɥɟɞɧɟɟ, ɤɚɤ ɩɪɚɜɢɥɨ,
ɜɵɬɟɤɚɟɬ ɢɡ ɮɢɡɢɱɟɫɤɨɝɨ ɤɨɧɬɟɤɫɬɚ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɡɚɞɚɱɢ. ɇɚɩɪɢɦɟɪ, ɞɥɹ
2
A
2
B
9
