Лыков С.Н., Гасумянц В.Э., Рыков С.А. Квантовая механика. Учебное пособие
Подождите немного. Документ загружается.

ɢ ɩɟɪɟɣɞɟɦ ɤ ɛɟɡɪɚɡɦɟɪɧɨɣ ɤɨɨɪɞɢɧɚɬɧɨɣ ɩɟɪɟɦɟɧɨɣ [ ɫɥɟɞɭɸɳɢɦ ɨɛɪɚɡɨɦ:
¸
¹
·
¨
©
§
H
[
F
x
x
0
1
.
ɷ
ɫɩɟɤɬɪ ɞɨɥɠɟɧ ɛɵɬɶ ɧɟɩɪɟɪɵɜɧɵɦ.
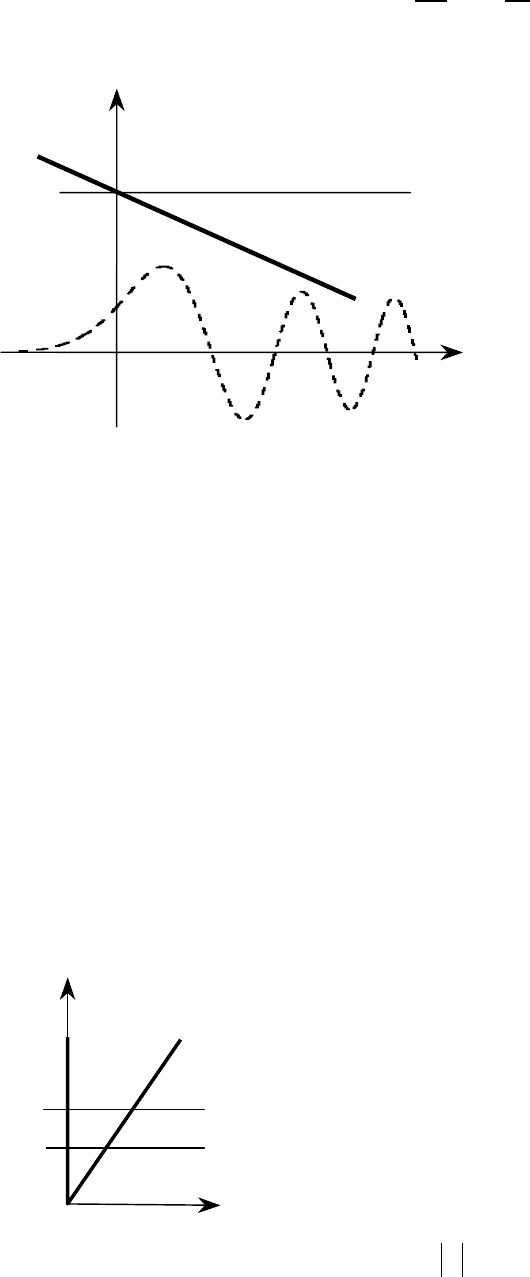
Ʉɨɨɪɞɢɧɚɬɚ (3) ɜɵɛɪɚɧɚ ɬɚɤ, ɱɬɨ ɩɪɢ
(3)
ɉɨɫɤɨɥɶɤɭ ɩɨɥɟ (1) ɧɟ ɹɜɥɹɟɬɫɹ
ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɨɣ, ɧɟɪɝɟɬɢɱɟɫɤɢɣ
)([
U
ɥɸɛɨɦ ɡɚɪɚɧɟɟ ɡɚɞɚɧɧɨɦ ɡɧɚɱɟɧɢɢ
ɷɧɟɪɝɢɢ
H
ɜ ɨɱɤɟ 0 [ ɢɦɟɟɦɬ H
U
(ɫɦ. ɪɢɫ. 5.9).
ɍɪɚɜ
)
ɧɟɧɢɟ (2) ɩɪɢɧɢɦɚɟɬ ɜɢɞ
0)(( [\[[\
cc
. (4)
Ɉɛɳɟɟ ɪɟɲɟɧɢɟ )([M ɭɪɚɜɧɟɧɢɹ
(4), ɤɚɤ ɢɡɜɟɫɬɧɨ ɢɡ ɥɢɬɟɪɚɬɭɪɵ ɩɨ
ɫɩɟɰɢɚɥɶɧɵɦ ɮɭɧɤɰɢɹɦ, ɦɨɠɧɨ
ɤɰɢɣ ɗɣɪɢ )(Ai z ɢ )(Bi z :ɩɪɟɞɫɬɚɜɢɬɶ ɥɢɧɟɣɧɨɣ ɤɨɦɛɢɧɚɰɢɟɣ ɮɭɧ
[M )( [ )(Bi
2
(Ai
1
C )[C . (5)
Ɏɭɧɤɰɢɹ ɤɨɧɟɱɧɚ ɩɪɢ )(Ai [f[f ; ɨɧɚ ɦɨɧɨɬɨɧɧɨ ɭɛɵɜɚɟɬ ɩɪɢ
ɭɫɬɪɟɦɥɟɧɢɢ ɤɨɨɪɞɢɧɚɬɵ ɜ ɨɛɥɚɫɬɶ ɡɧɚɱɟɧɢɣ[ 0
[
ɢ ɨɫɰɢɥɥɢɪɭɟ ɛɥɚɫ
ɂɦɟɧɧɨ ɬɚɤɨɝɨ ɩɨɜɟɞɟɧɢɹ ɦɵ ɠɞɟɦ ɨɬ ɜ ɫɬɚ
ɫɨɫɬɨɹɧɢɹ ɱɚɫ ɩɨɥɟ, ɩɨɤɚɡɚɧɧɨ
ɢɡɨɛɪɚɠɟɧ ɩɭɧɤɬɢɪɧɨɣ ɥɢɧɢɟɣ). Ɏɭɧɤɰɢ
ɬɜɨ ɬɢ
0![ . ɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɰɢɨɧɚɪɧɨɝɨ
ɦ ɧɚ ɪɢɫ. 5.9 (ɝɪɚɮɢɤ \ ɫɯɟɦɚɬɢɱɧɨ
ɹɠɟ )(Bi
ɬɢɰɵ ɜ
[
ɧɟɨɝɪɚɧɢɱɟɧɧɨ ɜ ɚɫɬɚɟɬ
ɩɪɢ fo[ , ɢ ɩɨɷɬɨɦɭ ɤɨɷɮɮɢɰɢɟɧɬ
2
C ɜ (5) ɫɥɟɞɭ
ɨɡɪ
ɬ ɜɵɛɪɚɬɶ ɧɭɥɸ.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɢɫɤɨɦɵɟ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɫɬɚɰɢɨɧɚɪɧɵɯ
ɢɦɟɸɬ ɜɢɞ:
ɟ ɪɚɜɧɵɦ
ɫɨɫɬɨɹɧɢɣ
C
x
\ )(
0
/)Ai x/(xFH (6)
ɝɞɟ
,
C
– ɧɨɪɦɢɪɨɜɨɱɧɚɹ ɨɹɧɧɚɹ. Ȼɨɥɟɟ ɞɟɬɚɥɶɧɨɟ
ɨɛɫɭɠɞɟɧɢɟ ɪɚɫɫɦɨɬɪɟɧɧɨɣ ɡɚɞɚɱɢ ɱɢɬɚɬɟɥɶ ɦɨɠɟɬ ɧɚɣɬɢ
ɜ [1,7].
ɛ) ɍɱɢɬɵɜɚɹ ɨɬɪɢɰɚɬɟɥɶɧɵɣ ɡɧɚɤ ɡɚɪɹɞɚ ɷɥɟɤɬɪɨɧɚ,
ɡɚɩɢɲɟɦ ɭɤɚɡɚɧɧ ɜ ɭɫɥɨɜɢɢ ɡɚɞɚɱɢ ɩɨɬɟɧɰɢɚɥ ɜ ɜɢɞɟ:
ɩɨɫɬ
ɵɣ
¯
®
f 0, x
ɝɞɟ
!
0,
)(
xxF
xU , (7)
0! { EeeEF (ɫɦ. ɪɢɫ.5.10).
H
)([\
[
0
Ɋɢɫ. 5.9
x
H
0
Ɋɢɫ. 5.10
U(x)
H
1
20

ɋɥɟɞ ɫɱɢɬɚɬɶ, ɱɬɨ 0)( \ɭɟɬ
x
ɩɪɢ 0
x
, ɩɪɢɱɟɦ ɜ ɨɱɤɟ 0 ɬ
x
ɟ ɬɪɟɛɭɟɬɫɹ
ɧɟɩɪɟɪɵɜɧɨɫɬɢ ɩɪɨɢɡɜɨɞɧɨɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ, ɚ ɥɢɲɶ
ɧ
ɝɪɚɧɢɱɧɨɟɧɚɥɚɝɚɟɬɫɹ
ɭɫɥɨɜɢɟ, ɨɛɟɫɩɟɱɢɜɚɸɳɟɟ ɧɟɩɪɟɪɵɜɧɨɫɬɶ ɫɚɦɨɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ )(
x
\ :
0)0( \ . (8)
ɋ ɩɨɦɨɳɶɸ ɧɨɜɨɣ ɤɨɨɪɞɢɧɚɬɧɨɣ ɩɟɪɟɦɟɧɧɨɣ
¸
·
¨
§
H
x
1
,
¹
Fx
0
ɝɞɟ
3/12
0
)2/( Fmx = ,
©
[ (9)
ɭɪɚɜɧɟɧɢɟ ɒɪɟɞɢɧɝɟɪɚ ɩɪɢɜɨɞɢɬɫɹ ɤ ɜɢɞɭ
0)()( [\[[\
cc
. (10)
Ɉɛɳɟɟ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (10) ɩɪɟɞɫɬ
ɮɭɧɤɰɢɣ ɗɣɪɢ
ɚɜɥɹɟɬɫɹ ɥɢɧɟɣɧɨɣ ɤɨɦɛɢɧɚɰɢɟɣ
)(Ai [ ɢ . Ɉɞɧɚɤɨ ɩɨɫɥɟɞɧɹɹ ɢɡ ɭɤɚɡɚɧɧɵɯ ɮɭɧɤɰɢɣ
ɪɚɧɢɱɟɧɧɨ ɜɨɡɪɚɫɬɚɟɬ ɩɪɢ
)(Bi [
ɧɟɨɝ fo[ ,
ɒɪɟɞɢɧɝɟɪɚ
ɬɚɤ ɱɬɨ, ɜ ɫɢɥɭ ɭɫɥɨɜɢɹ ɨɝɪɚɧɢɱɟɧɧɨɫɬɢ
ɢɫɤɨɦɵɯ ɪɟɲɟɧɢɣ ɭɪɚɜɧɟɧɢɹ , ɧɟɨɛɯɨɞɢɦɨ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɢ )(Bi [
ɜɵɛɪɚɬɶ ɪɚɜɧɵɦ ɧɭɥɸ. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɤɨɧɟɱɧɨɟ ɩɪɢ ɜɫɟɯ ɡɧɚɱɟɧɢɹɯ
x
ɪɟɲɟɧɢɟ
ɭɪɚɜɧɟɧɢɹ (10) ɢɦɟɟɬ ɜɢɞ
C
x
\ )(
0
/) xF/(Ai x H . (11)
Ƚɪɚɧɢɱɧɨɟ ɭɫɥɨɜɢɟ (8) ɫ ɭɱɟɬɨɦ (11) ɢɝɪɚɟɬ ɪɨɥɶ ɭɪɚɜɧɟɧɢɹ, ɤɨɬɨɪɵɦ
ɨɩɪɟɞɟɥɹɟɬɫɹ ɷɧɟ ɱɟɫɤɢ ɤɬɪ ɱɚɫɬɢɰɵ ɜ ɩɨɥɟ (7): ɪɝɟɬɢ ɣ ɫɩɟ
0Ai
0
/ H x .(12)
ɂɡ (12) ɫɥɟɞɭɟɬ, ɱɬɨ ɭɪɨɜɧɢ ɷɧɟɪɝɢɢ
n
F
H ɞɚɸɬɫɹ ɮɨɪɦɭɥɨɣ
H )()2/(
3/122
0
nnn
mFxF [ [ = , (13)
ɝɞɟ , , , … – ɤɨɪɧɢ ɭɪɚɜɧɟɧɢɹ
0
[
12
[[ 0)(Ai [ (ɧɭɥɢ ɮɭɧɤɰɢɢ ɗɣɪɢ). Ɂɧɚɱɟɧɢɹ
n
[ ɨɬɪɢɰɚɬɟɥɶɧɵ, ɬɚɤ ɤɚɤ ɮɭɧɤɰɢɹ )(Ai [ ɢɦɟɟɬ ɨɫɰɢɥɥɢɪɭɸɳɢɣ ɯɚɪɚɤɬɟɪ ɩɪɢ
0[ . ɉɨɞɫɬɚɜɥɹɹ ɞɨɩɭɫɬɢɦɵɟ ɡɧɚɱɟɧɢɹ ɷɧɟɪɝɢɢ (13) ɜ (11), ɩɨɥɭɱɚɟɦ
ɩɨɫɥɟɞɨɜɚɬɟɥɶɧɨɫɬɶ ɜɨɥɧɨɜɵɯ ɮɭɧɤɰɢɣ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ ɱɚɫɬɢɰɵ ɜ
ɩɨɥɟ (7):
Cx
n
\ )(
0
/)/(Ai xFx
n
H . (14)
ɉɨɫɬɨɹɧɧɚɹ
C
ɨɩɪɟɞɟɥɹɟɬɫɹ ɢɡ ɭɫɥɨɜɢɹ ɧɨɪɦɢɪɨɜɤɢ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ
ɟɞɢɧɢɰɭ.
ɧɚ
21

Ƚɥɚɜɚ 6. ɁȺȾȺɑɂ ɈȻ ɈɋɐɂɅɅəɌɈɊȺɏ
Ʉ ɩɪɟɞɫɬɚɜɥɟɧɢɸ ɨ ɝɚɪɦɨɧɢɱɟɫɤɨɦ ɨɫɰɢɥɥɹɬɨɪɟ ɩɪɢɜɨɞɢɬ ɪɚɫɫɦɨɬɪɟɧɢɟ
ɞɢɧɚɦɢɤɢ ɮɢɡɢɱɟɫɤɨɣ ɫɢɫɬɟɦɵ ɜɛɥɢɡɢ ɟɟ ɩɨɥɨɠɟɧɢɹ ɭɫɬɨɣɱɢɜɨɝɨ ɪɚɜɧɨɜɟɫɢɹ.
ȼ ɬɨɱɤɟ ɪɚɜɧɨɜɟɫɢɹ ɩɨɬɟɧɰɢɚɥɶɧɚɹ ɷɧɟɪɝɢɹ ɫɢɫɬɟɦɵ ɢɦɟɟɬ ɦɢɧɢɦɭɦ. ɉɨɷɬɨɦɭ
ɡɚɜɢɫɢɦɨɫɬɶ ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɷɧɟɪɝɢɢ ɨɬ ɤɨɨɪɞɢɧɚɬɵ
x
, ɯɚɪɚɤɬɟɪɢɡɭɸɳɟɣ
ɨɬɤɥɨɧɟɧɢɟ ɨɬ ɩɨɥɨɠɟɧɢɹ ɪɚɜɧɨɜɟɫɢɹ, ɜ ɩɟɪɜɨɦ ɩɪɢɛɥɢɠɟɧɢɢ ɩɨ ɫɬɟɩɟɧɹɦ
ɬɚɤɨɣ ɤɨɨɪɞɢɧɚɬɵ ɹɜɥɹɟɬɫɹ ɤɜɚɞɪɚɬɢɱɧɨɣ:
2/)(
2
xKxU , 0!
K
. (I)
ȼ ɫɥɭɱɚɟ ɱɚɫɬɢɰɵ ɦɚɫɫɵ ɟɟ ɨɞɧɨɦɟɪɧɨɟ ɞɜɢɠɟɧɢɟ ɫ ɩɨɬɟɧɰɢɚɥɶɧɨɣ
ɷɧɟɪɝɢɟɣ (I) ɜ ɤɥɚɫɫɢɱɟɫɤɨɣ ɦɟɯɚɧɢɤɟ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɝɚɪɦɨɧɢɱɟɫɤɨɟ
ɤɨɥɟɛɚɧɢɟ ɫ ɱɚɫɬɨɬɨɣ
m
mK /
0
Z . (II)
ȼ ɫɜɹɡɢ ɫ ɷɬɢɦ ɜɵɪɚɠɟɧɢɟ (I) ɧɚɡɵɜɚɸɬ ɩɨɬɟɧɰɢɚɥɨɦ ɝɚɪɦɨɧɢɱɟɫɤɨɝɨ
ɨɫɰɢɥɥɹɬɨɪɚ (oscillate – ɧɚ ɚɧɝɥɢɣɫɤɨɦ ɨɡɧɚɱɚɟɬ ɤɨɥɟɛɚɬɶɫɹ, ɜɢɛɪɢɪɨɜɚɬɶ). ȼ
ɤɥɚɫɫɢɱɟɫɤɨɣ ɦɟɯɚɧɢɤɟ ɩɨɥɧɚɹ ɷɧɟɪɝɢɹ ɨɫɰɢɥɥɹɬɨɪɚ H – ɫɭɦɦɚ ɤɢɧɟɬɢɱɟɫɤɨɣ
ɷɧɟɪɝɢɢ ɢ ɩɨɬɟɧɰɢɚɥɶɧɨɣ – ɦɨɠɟɬ ɩɪɢɧɢɦɚɬɶ ɥɸɛɨɟ ɡɧɚɱɟɧɢɟ, ɱɬɨ
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɜɨɡɦɨɠɧɨɫɬɢ ɡɚɞɚɬɶ ɩɪɨɢɡɜɨɥɶɧɭɸ ɜɟɥɢɱɢɧɭ ɚɦɩɥɢɬɭɞɵ
ɤɨɥɟɛɚɧɢɣ (ɩɪɢ ɷɬɨɦ ɞɥɹ ɩɪɢɦɟɧɢɦɨɫɬɢ ɩɪɢɛɥɢɠɟɧɢɹ (I) ɚɦɩɥɢɬɭɞɚ ɤɨɥɟɛɚɧɢɣ
ɨɫɰɢɥɥɹɬɨɪɚ, ɤɨɧɟɱɧɨ, ɞɨɥɠɧɚ ɛɵɬɶ ɞɨɫɬɚɬɨɱɧɨ ɦɚɥɨɣ). ȼ ɤɜɚɧɬɨɜɨɣ ɠɟ
ɦɟɯɚɧɢɤɟ ɜɫɟ ɫɬɚɰɢɨɧɚɪɧɵɟ ɫɨɫɬɨɹɧɢɹ ɨɫɰɢɥɥɹɬɨɪɚ ɩɪɢɧɚɞɥɟɠɚɬ ɞɢɫɤɪɟɬɧɵɦ
ɭɪɨɜɧɹɦ ɷɧɟɪɝɢɢ:
)2/1(
0
Z H n
n
= , ...,2,1,0 n . (III)
Ɉɬɥɢɱɢɬɟɥɶɧɨɣ ɱɟɪɬɨɣ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɫɩɟɤɬɪɚ ɝɚɪɦɨɧɢɱɟɫɤɨɝɨ
ɨɫɰɢɥɥɹɬɨɪɚ ɜ ɤɜɚɧɬɨɜɨɣ ɦɟɯɚɧɢɤɟ ɹɜɥɹɟɬɫɹ ɬɨ, ɱɬɨ ɭɪɨɜɧɢ ɷɧɟɪɝɢɢ (III)
ɪɚɫɩɨɥɨɠɟɧɵ ɱɟɪɟɡ ɪɚɜɧɵɟ ɢɧɬɟɪɜɚɥɵ
0
Z= . ɗɬɨɬ ɮɚɤɬ ɢɝɪɚɟɬ
ɮɭɧɞɚɦɟɧɬɚɥɶɧɭɸ ɪɨɥɶ ɜɨ ɦɧɨɝɢɯ ɡɚɞɚɱɚɯ ɨ ɞɢɧɚɦɢɤɟ ɫɥɨɠɧɵɯ ɫɢɫɬɟɦ ɜɛɥɢɡɢ
ɬɨɱɤɢ ɦɢɧɢɦɭɦɚ ɷɧɟɪɝɢɢ, ɩɨɡɜɨɥɹɹ ɜɜɟɫɬɢ ɩɪɟɞɫɬɚɜɥɟɧɢɟ ɨ «ɤɜɚɡɢɱɚɫɬɢɰɚɯ» –
ɤɜɚɧɬɚɯ ɷɧɟɪɝɢɢ , ɨɬɜɟɱɚɸɳɢɯ ɪɚɡɥɢɱɧɵɦ ɤɨɥɟɛɚɬɟɥɶɧɵɦ ɦɨɞɚɦ ɫɢɫɬɟɦɵ
(
k
Z=
k – ɧɨɦɟɪ ɦɨɞɵ).
ȼ ɤɜɚɧɬɨɜɨɣ ɦɟɯɚɧɢɤɟ ɤɥɚɫɫɢɱɟɫɤɚɹ ɤɚɪɬɢɧɚ ɤɨɥɟɛɚɧɢɣ ɨɫɰɢɥɥɹɬɨɪɚ
)(
t
x
ɭɬɪɚɱɢɜɚɟɬ ɫɦɵɫɥ. Ʉɨɝɞɚ ɝɨɜɨɪɹɬ ɨ ɤɨɥɟɛɚɧɢɹɯ ɤɜɚɧɬɨɜɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ,
ɧɚɩɪɢɦɟɪ, ɜɞɨɥɶ ɨɫɢ
x
, ɬɨ ɨɛɵɱɧɨ ɢɦɟɸɬ ɜɜɢɞɭ ɫɬɚɰɢɨɧɚɪɧɵɟ ɫɨɫɬɨɹɧɢɹ,
ɨɩɢɫɵɜɚɟɦɵɟ ɜɨɥɧɨɜɵɦɢ ɮɭɧɤɰɢɹɦɢ
)(x
n
\ . əɜɧɵɣ ɜɢɞ ɬɚɤɢɯ ɮɭɧɤɰɢɣ ɭɤɚɡɚɧ
ɧɢɠɟ ɜ ɪɟɲɟɧɢɹɯ ɡɚɞɚɱ.
22

Ɂɚɞɚɱɢ
6.1.
Ʌɢɧɟɣɧɵɣ ɨɫɰɢɥɥɹɬɨɪ ɫ ɷɥɟɤɬɪɢɱɟɫɤɢɦ ɡɚɪɹɞɨɦ ɩɨɦɟɳɟɧ ɜ
ɨɞɧɨɪɨɞɧɨɟ ɷɥɟɤɬɪɢɱɟɫɤɨɟ ɩɨɥɟ
E , ɧɚɩɪɚɜɥɟɧɧɨɟ ɜɞɨɥɶ ɨɫɢ ɤɨɥɟɛɚɧɢɣ.
q
ɚ) Ɉɩɪɟɞɟɥɢɬɶ ɷɧɟɪɝɟɬɢɱɟɫɤɢɣ ɫɩɟɤɬɪ ɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɫɬɚɰɢɨɧɚɪɧɵɯ
ɫɨɫɬɨɹɧɢɣ.
ɛ) ɇɚɣɬɢ ɩɨɥɹɪɢɡɭɟɦɨɫɬɶ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ. ɍɤɚɡɚɧɢɟ.
ɉɨɥɹɪɢɡɭɟɦɨɫɬɶɸ E ɨɩɪɟɞɟɥɹɟɬɫɹ ɜ ɥɢɧɟɣɧɨɦ ɩɪɢɛɥɢɠɟɧɢɢ ɩɨ ɫɥɚɛɨɦɭ
ɜɧɟɲɧɟɦɭ ɩɨɥɸ ɢɧɞɭɰɢɪɨɜɚɧɧɵɣ ɷɬɢɦ ɩɨɥɟɦ ɞɢɩɨɥɶɧɵɣ ɷɥɟɤɬɪɢɱɟɫɤɢɣ
ɦɨɦɟɧɬ (),ɚ ɬɚɤɠɟ, ɜ ɤɜɚɞɪɚɬɢɱɧɨɦ ɩɪɢɛɥɢɠɟɧɢɢ, – ɫɞɜɢɝ
ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɭɪɨɜɧɹ:.
E
Ed E
2/
2
EE H'
6.2 ɚ) ɇɚɣɬɢ ɭɪɨɜɧɢ ɷɧɟɪɝɢɢ ɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ),,( zy
x
\ ɫɬɚɰɢɨɧɚɪɧɵɯ
ɫɨɫɬɨɹɧɢɣ ɱɚɫɬɢɰɵ ɦɚɫɫɵ m , ɫɨɜɟɪɲɚɸɳɟɣ ɬɪɟɯɦɟɪɧɨɟ ɞɜɢɠɟɧɢɟ ɜ ɩɨɥɟ
2
3
2
2
2
1
2
1
)( zKyKxKU
r ,
ɝɞɟ – ɡɚɞɚɧɧɵɟ ɩɨɥɨɠɢɬɟɥɶɧɵɟ ɩɚɪɚɦɟɬɪɵ. ɂɦɟɸɬ ɥɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ
ɨɩɪɟɞɟɥɟɧɧɭɸ ɱɟɬɧɨɫɬɶ ɩɨ ɨɬɧɨɲɟɧɢɸ ɤ ɩɪɟɨɛɪɚɡɨɜɚɧɢɸ ?
j
K
rr o
ɛ) Ɉɩɪɟɞɟɥɢɬɶ ɤɪɚɬɧɨɫɬɶ ɜɵɪɨɠɞɟɧɢɹ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɭɪɨɜɧɟɣ ɜ ɫɥɭɱɚɟ,
ɤɨɝɞɚ ɭɤɚɡɚɧɧɨɟ ɩɨɥɟ )(
r
U
ɨɛɥɚɞɚɟɬ ɨɫɶɸ ɜɪɚɳɚɬɟɥɶɧɨɣ ɫɢɦɦɟɬɪɢɢ:
.
321
KKK z
ɜ) Ɉɩɪɟɞɟɥɢɬɶ ɤɪɚɬɧɨɫɬɶ ɜɵɪɨɠɞɟɧɢɹ ɬɚɤɠɟ ɜ ɬɨɦ ɫɥɭɱɚɟ, ɤɨɝɞɚ
ɭɤɚɡɚɧɧɨɟ ɩɨɥɟ ɨɛɥɚɞɚɟɬ ɫɮɟɪɢɱɟɫɤɨɣ ɫɢɦɦɟɬɪɢɟɣ:
321
KKK .
6.3 ɇɚɣɬɢ ɭɪɨɜɧɢ ɷɧɟɪɝɢɢ ɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ
ɱɚɫɬɢɰɵ ɜ ɩɨɥɟ
¸
¸
¹
·
¨
¨
©
§
Z
zy
zy
x
m
zyxU
22
),,(
22
2
2
0
.
6.4 ɇɚɣɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɜɟɪɨɹɬɧɨɫɬɢ ɞɥɹ ɡɧɚɱɟɧɢɣ ɢɦɩɭɥɶɫɚ ɜ
ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɹɯ ɥɢɧɟɣɧɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ.
6.5. ɇɚɣɬɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɣ ɫɩɟɤɬɪ ɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ),,( zy
x
\
ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ ɛɟɫɫɩɢɧɨɜɨɣ ɱɚɫɬɢɰɵ ɫ ɷɥɟɤɬɪɢɱɟɫɤɢɦ ɡɚɪɹɞɨɦ ɜ
ɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ . ɉɨɥɟ ɡɚɞɚɧɨ ɩɨɫɪɟɞɫɬɜɨɦ ɜɟɤɬɨɪɧɨɝɨ
ɩɨɬɟɧɰɢɚɥɚ ɫ ɤɨɦɩɨɧɟɧɬɚɦɢ
q
B
A
ByA
x
,0
zy
AA .
23
6.6. ɍɛɟɞɢɬɶɫɹ ɜ ɬɨɦ, ɱɬɨ ɪɟɲɟɧɢɹ ɭɪɚɜɧɟɧɢɹ ɒɪɟɞɢɧɝɟɪɚ ɞɥɹ ɱɚɫɬɢɰɵ ɜ
ɨɞɧɨɪɨɞɧɨɦ ɦɚɝɧɢɬɧɨɦ ɩɨɥɟ, ɡɚɞɚɜɚɟɦɨɦ ɩɨɬɟɧɰɢɚɥɨɦ ɫ ɤɨɦɩɨɧɟɧɬɚɦɢ
A
ByA
x
,0
zy
AA ,
ɦɨɝɭɬ ɛɵɬɶ ɩɨɥɭɱɟɧɵ ɩɨɫɪɟɞɫɬɜɨɦ ɤɚɥɢɛɪɨɜɨɱɧɨɝɨ ɩɪɟɨɛɪɚɡɨɜɚɧɢɹ ɪɟɲɟɧɢɣ,
ɨɬɜɟɱɚɸɳɢɯ ɩɨɬɟɧɰɢɚɥɭ
A
~
ɫ ɤɨɦɩɨɧɟɧɬɚɦɢ
BxA
y
~
,.0
~~
zx
AA
6.7. Ⱦɥɹ ɥɢɧɟɣɧɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ ɫ ɦɚɫɫɨɣ ɢ ɱɚɫɬɨɬɨɣ ɜɜɟɞɟɦ ɜ
ɪɚɫɫɦɨɬɪɟɧɢɟ ɨɩɟɪɚɬɨɪɵ
a ɢ , ɨɩɪɟɞɟɥɹɟɦɵɟ ɪɚɜɟɧɫɬɜɚɦɢ:
m
0
Z
ˆ
a
ˆ
¸
¸
¹
·
¨
¨
©
§
Z
Z
0
0
ˆ
ˆ
2
ˆ
m
pi
x
m
a
=
,
¸
¸
¹
·
¨
¨
©
§
Z
Z
0
0
ˆ
ˆ
2
ˆ
m
pi
x
m
a
=
,
ɝɞɟ
x
ˆ
ɢ – ɨɩɟɪɚɬɨɪɵ ɤɨɨɪɞɢɧɚɬɵ ɢ ɢɦɩɭɥɶɫɚ.p
ˆ
ɚ) ȼɵɱɢɫɥɢɬɶ ɤɨɦɦɭɬɚɬɨɪ ɨɩɟɪɚɬɨɪɨɜ ɢa
ˆ
a
ˆ
.
ɛ) ɉɨɫɬɪɨɢɬɶ ɫɢɫɬɟɦɭ ɫɨɛɫɬɜɟɧɧɵɯ ɜɟɤɬɨɪɨɜ ɢ ɧɚɣɬɢ ɫɩɟɤɬɪ ɫɨɛɫɬɜɟɧɧɵɯ
ɡɧɚɱɟɧɢɣ ɨɩɟɪɚɬɨɪɚ , ɩɨɥɶɡɭɹɫɶ ɤɨɦɦɭɬɚɬɨɪɨɦ ɨɩɟɪɚɬɨɪɨɜ ,.aa
ˆˆ
a
ˆ
a
ˆ
ɜ) ȼɵɪɚɡɢɬɶ ɝɚɦɢɥɶɬɨɧɢɚɧ ɨɫɰɢɥɥɹɬɨɪɚ ɱɟɪɟɡ ɨɩɟɪɚɬɨɪ .aa
ˆˆ
6.8. ɉɭɫɬɶ n – ɧɨɪɦɢɪɨɜɚɧɧɵɟ ɫɬɚɰɢɨɧɚɪɧɵɟ ɫɨɫɬɨɹɧɢɹ ɥɢɧɟɣɧɨɝɨ
ɨɫɰɢɥɥɹɬɨɪɚ ɫ ɦɚɫɫɨɣ m ɢ ɫɨɛɫɬɜɟɧɧɨɣ ɱɚɫɬɨɬɨɣ
0
Z
. ɇɚɣɬɢ:
ɚ) Ɇɚɬɪɢɱɧɵɟ ɷɥɟɦɟɧɬɵ
nxn
ˆ
c
ɨɩɟɪɚɬɨɪɚ ɤɨɨɪɞɢɧɚɬɵ ɨɫɰɢɥɥɹɬɨɪɚ.
ɛ) ɋɪɟɞɧɟɟ ɡɧɚɱɟɧɢɟ ɤɜɚɞɪɚɬɚ ɤɨɨɪɞɢɧɚɬɵ ɜ ɫɬɚɰɢɨɧɚɪɧɨɦ ɫɨɫɬɨɹɧɢɢ.
6.9. ȼ ɧɚɱɚɥɶɧɵɣ ɦɨɦɟɧɬ ɜɪɟɦɟɧɢ (0
t
) ɫɨɫɬɨɹɧɢɟ ɝɚɪɦɨɧɢɱɟɫɤɨɝɨ
ɨɫɰɢɥɥɹɬɨɪɚ ɡɚɞɚɧɨ ɜ ɜɢɞɟ ɫɥɟɞɭɸɳɟɣ ɫɭɩɟɪɩɨɡɢɰɢɢ ɜɫɟɯ ɟɝɨ ɫɬɚɰɢɨɧɚɪɧɵɯ
ɫɨɫɬɨɹɧɢɣ
n :
n
n
e
n
n
t
¦
f
D
D
D
0
2/
0
!
2
,
ɝɞɟ – ɩɪɨɢɡɜɨɥɶɧɨɟ ɤɨɦɩɥɟɤɫɧɨɟ ɱɢɫɥɨ. ɉɪɢɧɹɬɨ ɧɚɡɵɜɚɬɶD
D ɤɨɝɟɪɟɧɬɧɵɦ
ɫɨɫɬɨɹɧɢɟɦ.
ɚ) Ɉɩɪɟɞɟɥɢɬɶ ɡɚɜɢɫɢɦɨɫɬɶ ɨɬ ɜɪɟɦɟɧɢ ɫɪɟɞɧɟɝɨ ɡɧɚɱɟɧɢɹ ɤɨɨɪɞɢɧɚɬɵ
ɨɫɰɢɥɥɹɬɨɪɚ ɜ ɤɨɝɟɪɟɧɬɧɨɦ ɫɨɫɬɨɹɧɢɢ.
ɛ) ɇɚɣɬɢ ɪɚɫɩɪɟɞɟɥɟɧɢɟ ɜɟɪɨɹɬɧɨɫɬɢ ɞɥɹ ɱɢɫɥɚ ɤɜɚɧɬɨɜ ɜ
ɤɨɝɟɪɟɧɬɧɨɦ ɫɨɫɬɨɹɧɢɢ ɨɫɰɢɥɥɹɬɨɪɚ, ɜɵɱɢɫɥɢɬɶ ɫɪɟɞɧɢɟ ɡɧɚɱɟɧɢɹ ɢ .
n
Wn
n
2
n
24

6.10. Ɋɚɫɫɦɚɬɪɢɜɚɟɬɫɹ ɤɜɚɧɬɨɜɚɹ ɫɢɫɬɟɦɚ, ɢɦɟɸɳɚɹ ɬɨɥɶɤɨ ɞɜɚ
ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɹ:
0–ɨɫɧɨɜɧɨɟ ɫɨɫɬɨɹɧɢɟ ɫ ɷɧɟɪɝɢɟɣ 0,
0
H 1–
ɜɨɡɛɭɠɞɟɧɧɨɟ ɫɨɫɬɨɹɧɢɟ ɫ ɷɧɟɪɝɢɟɣ
01
H
!H . ɗɬɢ ɫɨɫɬɨɹɧɢɹ ɨɛɪɚɡɭɸɬ ɩɨɥɧɵɣ
ɨɪɬɨɧɨɪɦɢɪɨɜɚɧɧɵɣ ɛɚɡɢɫ. ɉɭɫɬɶ – «ɩɨɧɢɠɚɸɳɢɣ» ɨɩɟɪɚɬɨɪ,
ɯɚɪɚɤɬɟɪɢɡɭɸɳɢɣɫɹ ɪɚɜɟɧɫɬɜɚɦɢ:
c
ˆ
c
ˆ
1 0 , c
ˆ
00 .
ȼ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɦ ɫɥɭɱɚɟ ɬɚɤɨɣ ɨɩɟɪɚɬɨɪ ɩɪɢɧɹɬɨ ɧɚɡɵɜɚɬɶ ɮɟɪɦɢɨɧɧɵɦ
ɨɩɟɪɚɬɨɪɨɦ ɭɧɢɱɬɨɠɟɧɢɹ.
ɚ) ɍɫɬɚɧɨɜɢɬɶ ɪɟɡɭɥɶɬɚɬ ɞɟɣɫɬɜɢɹ ɨɩɟɪɚɬɨɪɚ
c
ˆ
ɧɚ ɭɤɚɡɚɧɧɵɟ ɛɚɡɢɫɧɵɟ
ɫɨɫɬɨɹɧɢɹ
0,1.
ɛ) ɉɪɨɜɟɪɢɬɶ, ɱɬɨ ɨɩɟɪɚɬɨɪɵ ,c
ˆ
c
ˆ
ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɪɚɜɟɧɫɬɜɚɦ
1}
ˆ
,
ˆ
{
cc , }
ˆ
,
ˆ
{ cc 0}
ˆ
,
ˆ
{
cc ,
ɝɞɟ ɮɢɝɭɪɧɵɦɢ ɫɤɨɛɤɚɦɢ ɨɛɨɡɧɚɱɟɧ ɚɧɬɢɤɨɦɦɭɬɚɬɨɪ ɨɩɟɪɚɬɨɪɨɜ,
ɨɩɪɟɞɟɥɹɟɦɵɣ ɮɨɪɦɭɥɨɣ:.ABBABA
ˆ
ˆˆ
ˆ
}
ˆ
,
ˆ
{ {
ɜ) ɉɨɤɚɡɚɬɶ, ɱɬɨ ɝɚɦɢɥɶɬɨɧɢɚɧ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɣ ɫɢɫɬɟɦɵ ɦɨɠɟɬ ɛɵɬɶ
ɩɪɟɞɫɬɚɜɥɟɧ ɜ ɜɢɞɟ
1
ˆ
H H
c
ˆ
c
ˆ
.
Ɋɟɲɟɧɢɹ
6.1. ɚ) Ʉɚɤ ɢɡɜɟɫɬɧɨ, ɩɨɬɟɧɰɢɚɥɶɧɚɹ ɷɧɟɪɝɢɹ ɨɛɵɱɧɨɝɨ ɥɢɧɟɣɧɨɝɨ
ɨɫɰɢɥɥɹɬɨɪɚ ɪɚɜɧɚ
222
0
2
1
2
1
)( xKxmxU {Z , (1)
ɝɞɟ – ɦɚɫɫɚ ɱɚɫɬɢɰɵ, – ɫɨɛɫɬɜɟɧɧɚɹ ɱɚɫɬɨɬɚ ɤɨɥɟɛɚɧɢɣ. ɉɪɢ ɷɬɨɦ
ɭɪɚɜɧɟɧɢɟ ɒɪɟɞɢɧɝɟɪɚ
m
0
Z
)()(
ˆ
xxH \H \ (2)
ɫ ɝɚɦɢɥɶɬɨɧɢɚɧɨɦ
22
0
2
22
2
1
2
ˆˆ
xm
xd
d
m
HH
ɨɫɰ
Z
=
(3)
ɞɚɟɬ ɫɩɟɤɬɪ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɭɪɨɜɧɟɣ
)2/1(
0
Z H n
n
= , ...,2,1,0
n , (4)
25

ɢ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ ɨɫɰɢɥɥɹɬɨɪɚ:
¸
¸
¹
·
¨
¨
©
§
Z
¸
¸
¹
·
¨
¨
©
§
Z
¸
¸
¹
·
¨
¨
©
§
S
Z
{\
===
00
2
4/1
0
2
exp
!2
1
)(
m
xH
m
x
n
m
x
n
n
ɨɫɰ
n
, (5)
ɝɞɟ ) – ɩɨɥɢɧɨɦɵ ɗɪɦɢɬɚ (([
n
H 1)(
0
[H , [
[
2)(
1
H , , …).
Ɏɭɧɤɰɢɢ (5) ɜɟɳɟɫɬɜɟɧɧɵ, ɧɨɪɦɢɪɨɜɚɧɵ ɧɚ ɟɞɢɧɢɰɭ ɢ ɜɡɚɢɦɧɨ ɨɪɬɨɝɨɧɚɥɶɧɵ:
24)(
2
2
[ [H
³
f
f
xd )(x
ɨɫɰ
n
\
nn
ɨɫɰ
n
x
c
c
G \ )( . (6)
ɉɪɢ ɧɚɥɨɠɟɧɢɢ ɧɚ ɡɚɪɹɠɟɧɧɵɣ ɨɫɰɢɥɥɹɬɨɪ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɩɨɥɹ ,
ɧɚɩɪɚɜɥɟɧɧɨɝɨ ɜɞɨɥɶ ɨɫɢ
E
x
, ɤ ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɷɧɟɪɝɢɢ (1) ɞɨɛɚɜɥɹɟɬɫɹ ɜɤɥɚɞ
x
E
q , ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɣ ɧɚɥɢɱɢɸ ɜɧɟɲɧɟɣ ɫɢɥɵ EF q . Ƚɚɦɢɥɶɬɨɧɢɚɧ
ɩɪɢɧɢɦɚɟɬ ɜɢɞ
xEqxm
xd
d
m
H Z
22
0
2
22
2
1
2
ˆ
=
. (7)
ɉɨɫɤɨɥɶɤɭ ɩɪɢ ɞɨɛɚɜɥɟɧɢɢ ɥɢɧɟɣɧɨɝɨ ɩɨ
x
ɱɥɟɧɚ ɯɚɪɚɤɬɟɪ ɤɜɚɞɪɚɬɢɱɧɨɣ
ɡɚɜɢɫɢɦɨɫɬɢ ɩɨɬɟɧɰɢɚɥɚ ɨɬ
x
ɫɨɯɪɚɧɹɟɬɫɹ, ɭɪɚɜɧɟɧɢɟ ɒɪɟɞɢɧɝɟɪɚ ɫ
ɝɚɦɢɥɶɬɨɧɢɚɧɨɦ (7) ɞɨɥɠɧɨ ɡɚɦɟɧɨɣ ɩɟɪɟɦɟɧɧɨɣ
0
~
xxx ɫɜɨɞɢɬɶɫɹ ɤ
ɭɪɚɜɧɟɧɢɸ ɒɪɟɞɢɧɝɟɪɚ ɞɥɹ ɨɛɵɱɧɨɝɨ ɥɢɧɟɣɧɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ. ɉɪɨɢɡɜɟɞɹ ɜ (7)
ɭɤɚɡɚɧɧɭɸ ɡɚɦɟɧɭ ɢ ɜɵɛɪɚɜ ɩɨɫɬɨɹɧɧɭɸ ɬɚɤ, ɱɬɨɛɵ ɫɥɚɝɚɟɦɨɟ, ɥɢɧɟɣɧɨɟ
ɨɬɧɨɫɢɬɟɥɶɧɨ ɧɨɜɨɣ ɩɟɪɟɦɟɧɧɨɣ
0
x
x
~
, ɢɫɱɟɡɥɨ, ɢɦɟɟɦ:
2
0
22
22
0
2
22
2
~
2
1
~
2
ˆ
Z
Z
m
Eq
xm
xd
d
m
H
=
, (8)
ɝɞɟ
2
0
~
Z
m
Eq
xx
. (9)
ɋɪɚɜɧɢɜɚɹ (8) ɫ (3), ɡɚɤɥɸɱɚɟɦ, ɱɬɨ ɢɫɤɨɦɵɦɢ ɫɨɛɫɬɜɟɧɧɵɦɢ ɮɭɧɤɰɢɹɦɢ ɞɥɹ
(7) ɢɥɢ (8) ɹɜɥɹɸɬɫɹ
\ \ )
~
()( xx
ɨɫɰ
nn
2
0
/ Z\ mEqx
ɨɫɰ
n
, (10)
ɚ ɷɧɟɪɝɟɬɢɱɟɫɤɢɣ ɫɩɟɤɬɪ ɢɦɟɟɬ ɜɢɞ:
2
0
22
0
2
2
1
Z
¸
¹
·
¨
©
§
Z H
m
Eq
n
n
= , , (11)...,2,1,0 n
26
Ɉɬɦɟɬɢɦ, ɱɬɨ ɜ ɤɥɚɫɫɢɱɟɫɤɨɣ ɦɟɯɚɧɢɤɟ ɜ ɡɚɞɚɱɟ ɨ ɥɢɧɟɣɧɨɦ ɨɫɰɢɥɥɹɬɨɪɟ
ɜɤɥɸɱɟɧɢɟ ɩɨɫɬɨɹɧɧɨɣ ɫɢɥɵ ɬɚɤɠɟ ɩɪɢɜɨɞɢɬ ɥɢɲɶ ɤ ɫɦɟɳɟɧɢɸ ɩɨɥɨɠɟɧɢɹ
ɪɚɜɧɨɜɟɫɢɹ ɨɫɰɢɥɥɹɬɨɪɚ ɧɚ ɜɟɥɢɱɢɧɭ ɢ ɤ ɫɞɜɢɝɭ ɦɢɧɢɦɭɦɚ
ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɷɧɟɪɝɢɢ ɧɚ .
F
2
00
/ Z mFx
2
0
2
2/ Z H' mF
ɛ) Ɏɨɪɦɭɥɚ (11) ɩɨɤɚɡɵɜɚɟɬ, ɱɬɨ ɜɵɡɜɚɧɧɵɣ ɷɥɟɤɬɪɢɱɟɫɤɢɦ ɩɨɥɟɦ ɫɞɜɢɝ
ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɭɪɨɜɧɟɣ ɤɜɚɧɬɨɜɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ
n
H ɯɚɪɚɤɬɟɪɢɡɭɟɬɫɹ ɧɟ
ɡɚɜɢɫɹɳɟɣ ɨɬ ɜɟɥɢɱɢɧɨɣn
2
0
22
2 Z
H'
m
Eq
. (12)
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɩɨɥɹɪɢɡɭɟɦɨɫɬɶ E , ɨɩɪɟɞɟɥɹɟɦɚɹ ɢɡ ɮɨɪɦɭɥɵ ,
ɞɥɹ ɜɫɟɯ ɫɬɚɰɢɨɧɚɪɧɵɯ ɫɨɫɬɨɹɧɢɣ ɨɫɰɢɥɥɹɬɨɪɚ ɨɞɢɧɚɤɨɜɚ ɢ ɪɚɜɧɚ . ȼ
ɞɚɧɧɨɦ ɫɥɭɱɚɟ ɜɵɪɚɠɟɧɢɟ ɞɥɹ ɩɨɥɹɪɢɡɭɟɦɨɫɬɢ ɧɟ ɫɨɞɟɪɠɢɬ ɩɨɫɬɨɹɧɧɨɣ ɉɥɚɧɤɚ
ɢ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɢɦɟɟɬ ɤɥɚɫɫɢɱɟɫɤɢɣ ɯɚɪɚɤɬɟɪ.
2/
2
EE H'
2
0
2
/ Zmq
Ɉɩɪɟɞɟɥɢɜ ɨɩɟɪɚɬɨɪ ɷɥɟɤɬɪɢɱɟɫɤɨɝɨ ɞɢɩɨɥɶɧɨɝɨ ɦɨɦɟɧɬɚ (ɬɨɱɧɟɟ ɝɨɜɨɪɹ,
ɨɩɟɪɚɬɨɪ ɟɝɨ ɩɪɨɟɤɰɢɢ ɧɚ ɨɫɶ
x
) ɮɨɪɦɭɥɨɣ , ɞɥɹ ɫɪɟɞɧɟɝɨ ɡɧɚɱɟɧɢɹ
ɷɬɨɝɨ ɨɩɟɪɚɬɨɪɚ ɛɭɞɟɦ ɢɦɟɬɶ:
xqd
ˆ
ˆ
³
f
f
\
2
)(xxxdqxqd
n
. (13)
ɉɟɪɟɣɞɟɦ ɤ ɢɧɬɟɝɪɢɪɨɜɚɧɢɸ ɩɨ ɩɟɪɟɦɟɧɧɨɣ
0
~
xxx , ɝɞɟ :
2
00
/ Z mEqx
³
f
f
\
2
)
~
(
~~
xxxdqxqd
ɨɫɰ
n
³
f
f
\
2
0
)
~
(
~
xxdxq
ɨɫɰ
n
. (14)
ɉɟɪɜɨɟ ɫɥɚɝɚɟɦɨɟ ɜ ɩɪɚɜɨɣ ɱɚɫɬɢ (14) ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ, ɩɨɫɤɨɥɶɤɭ, ɤɚɤ ɦɨɠɧɨ
ɜɢɞɟɬɶ ɢɡ (5), ɮɭɧɤɰɢɢ ɨɛɥɚɞɚɸɬ ɨɩɪɟɞɟɥɟɧɧɨɣ ɱɟɬɧɨɫɬɶɸ (ɪɚɜɧɨɣ )
ɢ, ɫɥɟɞɨɜɚɬɟɥɶɧɨ, ɩɨɞɵɧɬɟɝɪɚɥɶɧɨɟ ɜɵɪɚɠɟɧɢɟ ɧɟɱɟɬɧɨ ɨɬɧɨɫɢɬɟɥɶɧɨ ɡɚɦɟɧɵ
ɨɫɰ
n
\
n
)1(
x
x
~~
o . ȼɬɨɪɨɟ ɫɥɚɝɚɟɦɨɟ ɜ (14) ɫ ɭɱɟɬɨɦ ɧɨɪɦɢɪɨɜɤɢ ɮɭɧɤɰɢɣ ɧɚ
ɟɞɢɧɢɰɭ ɪɚɜɧɨ . Ɍɚɤɢɦ ɨɛɪɚɡɨɦ,
ɨɫɰ
n
\
0
xq
E
m
q
xqd
2
0
2
0
Z
. (15)
ȼɢɞɧɨ, ɱɬɨ ɮɨɪɦɭɥɚ
Ed E ɞɚɟɬ ɞɥɹ ɩɨɥɹɪɢɡɭɟɦɨɫɬɢ E ɭɠɟ ɢɡɜɟɫɬɧɵɣ ɧɚɦ
ɪɟɡɭɥɶɬɚɬ:
E
2
0
2
/ Zmq . (16)
27

6.2. ɚ) ȼ ɞɚɧɧɨɣ ɡɚɞɚɱɟ ɝɚɦɢɥɶɬɨɧɢɚɧ ɱɚɫɬɢɰɵ ɦɨɠɧɨ ɡɚɩɢɫɚɬɶ ɜ ɜɢɞɟ
321
ˆˆˆˆ
HHHH
. (1)
Ɂɞɟɫɶ ɤɚɠɞɵɣ ɢɡ ɨɩɟɪɚɬɨɪɨɜ
22
2
2
1
2
ˆ
ˆ
kk
k
k
xm
m
p
H Z ,
m
K
k
k
{Z , (2)
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɝɚɦɢɥɶɬɨɧɢɚɧ ɥɢɧɟɣɧɨɝɨ ɨɫɰɢɥɥɹɬɨɪɚ ɢ ɫɜɹɡɚɧ ɬɨɥɶɤɨ ɫ
ɨɞɧɨɣ ɢɡ ɬɪɟɯ ɤɨɨɪɞɢɧɚɬɧɵɯ ɩɟɪɟɦɟɧɧɵɯ ( ɨɡɧɚɱɚɟɬ
k
x
x
, ɢɥɢ
ɫɨɨɬɜɟɬɫɬɜɟɧɧɨ ɡɧɚɱɟɧɢɹɦ 3
y z
,2,1 k ). ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɩɨɥɶɡɭɹɫɶ ɦɟɬɨɞɨɦ
ɪɚɡɞɟɥɟɧɢɹ ɩɟɪɟɦɟɧɧɵɯ, ɦɵ ɧɚɣɞɟɦ, ɱɬɨ ɫɨɛɫɬɜɟɧɧɵɟ ɮɭɧɤɰɢɢ ɝɚɦɢɥɶɬɨɧɢɚɧɚ
(1) ɪɚɜɧɵ ɩɪɨɢɡɜɟɞɟɧɢɸ ɜɨɥɧɨɜɵɯ ɮɭɧɤɰɢɣ ɥɢɧɟɣɧɵɯ ɨɫɰɢɥɥɹɬɨɪɨɜ:
\ ),,(
321
zyx
nnn
)(
1
x
ɨɫɰ
n
\ )(
2
y
ɨɫɰ
n
\ )(
3
z
ɨɫɰ
n
\ , (3)
ɝɞɟ ɮɭɧɤɰɢɢ )ɨɩɪɟɞɟɥɹɸɬɫɹ ɮɨɪɦɭɥɨɣ (5) ɜ ɡɚɞɚɱɟ 6.1. Ɏɭɧɤɰɢɢ (3)
ɨɛɥɚɞɚɸɬ ɱɟɬɧɨɫɬɶɸ . Ɉɧɢ ɨɛɪɚɡɭɸɬ ɨɪɬɨɧɨɪɦɢɪɨɜɚɧɧɭɸ ɫɢɫɬɟɦɭ:
(
k
ɨɫɰ
n
x
k
\
321
)1(
nnn
³
r
3
d )(
321
r
nnn
\ \
ccc
)(
321
r
nnn
11
nn
c
G
22
nn
c
G
33
nn
c
G . (4)
ɋɬɚɰɢɨɧɚɪɧɵɟ ɫɨɫɬɨɹɧɢɹ ɧɭɦɟɪɭɸɬɫɹ ɫɨɜɨɤɭɩɧɨɫɬɶɸ ɤɜɚɧɬɨɜɵɯ ɱɢɫɟɥ ,,
, ɧɟɡɚɜɢɫɢɦɨ ɞɪɭɝ ɨɬ ɞɪɭɝɚ ɩɪɢɧɢɦɚɸɳɢɯ ɡɧɚɱɟɧɢɹ 0, 1, 2, …. ɗɧɟɪɝɢɹ
ɫɬɚɰɢɨɧɚɪɧɨɝɨ ɫɨɫɬɨɹɧɢɹ ɪɚɜɧɚ ɫɭɦɦɟ ɬɪɟɯ ɜɤɥɚɞɨɜ, ɤɚɠɞɵɣ ɢɡ ɤɨɬɨɪɵɯ
ɨɬɜɟɱɚɟɬ ɨɞɧɨɦɟɪɧɨɦɭ ɤɨɥɟɛɚɧɢɸ ɨɫɰɢɥɥɹɬɨɪɚ ɜɞɨɥɶ
1
n
2
n
3
n
x
, ɢɥɢ ɫ
ɫɨɨɬɜɟɬɫɬɜɭɸɳɢɦɢ ɱɚɫɬɨɬɚɦɢ :
y z
k
Z
)2/1(
11
321
Z H n
nnn
= )2/1(
22
Z n= )2/1(
33
Z n= . (5)
ɛ) ȼ ɫɥɭɱɚɟ ɫ ɷɧɟɪɝɟɬɢɱɟɫɤɢɟ ɭɪɨɜɧɢ
021
Z{Z Z
)1(
210
321
Z H nn
nnn
= )2/1(
33
Z
n= (6)
ɫɨ ɜɫɟɜɨɡɦɨɠɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɢ , ɩɪɢ ɤɨɬɨɪɵɯ ɩɨɫɬɨɹɧɧɚ ɫɭɦɦɚ
1
n
2
n
1
n
2
n ,
ɨɤɚɡɵɜɚɸɬɫɹ ɜɵɪɨɠɞɟɧɧɵɦɢ. ɉɪɢ ɡɚɞɚɧɧɨɦ
21
nnN
{
ɦɨɠɟɦ ɩɨɥɚɝɚɬɶ
ɪɚɜɧɵɦ 0, … ,
1
n
N
(ɜɫɟɝɨ 1
N
ɡɧɚɱɟɧɢɣ), ɚ ɛɭɞɟɬ ɨɩɪɟɞɟɥɹɬɶɫɹ ɨɞɧɨɡɧɚɱɧɨ –
ɤɚɤ . Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɷɧɟɪɝɟɬɢɱɟɫɤɢɣ ɫɩɟɤɬɪ (6) ɯɚɪɚɤɬɟɪɢɡɭɟɬɫɹ (
2
n
1
nN 1
N
)-
ɤɪɚɬɧɵɦ ɜɵɪɨɠɞɟɧɢɟɦ ɢ ɦɨɠɟɬ ɛɵɬɶ ɡɚɩɢɫɚɧ ɜ ɜɢɞɟ:
)1(
0,
3
Z H N
nN
= )2/1(
33
Z n= ,
3
, nN 0, 1, 2, … . (7)
28

ɜ) ɋɥɭɱɚɸ ɫ
0321
Z{Z Z Z ɨɬɜɟɱɚɟɬ «ɫɮɟɪɢɱɟɫɤɢɣ» ɨɫɰɢɥɥɹɬɨɪ
(ɱɚɫɬɢɰɚ ɜ ɫɮɟɪɢɱɟɫɤɢ ɫɢɦɦɟɬɪɢɱɧɨɦ ɩɨɥɟ 2). Ɏɨɪɦɭɥɚ (5)
ɩɪɢɧɢɦɚɟɬ ɜɢɞ
/)(
22
0
rmU Z r
)2/3(
0
Z H n
n
= , (8)
ɝɞɟ . ɉɪɢ ɡɚɞɚɧɧɨɦ ɦɨɠɟɦ ɩɨɥɚɝɚɬɶ ɪɚɜɧɵɦ 0, … , , ɱɢɫɥɨ
ɛɭɞɟɬ ɩɪɢɧɢɦɚɬɶ ɡɧɚɱɟɧɢɹ 0, … ,
321
nnnn n
1
nn
2
n
1
nn (ɜɫɟɝɨ 1
1
nn ɡɧɚɱɟɧɢɣ), ɚ ɱɢɫɥɨ
ɨɩɪɟɞɟɥɢɬɫɹ ɨɞɧɨɡɧɚɱɧɨ – ɤɚɤ
3
n
21
nnn . ɋɥɟɞɨɜɚɬɟɥɶɧɨ, ɤɪɚɬɧɨɫɬɶ
ɜɵɪɨɠɞɟɧɢɹ ɭɪɨɜɧɟɣ ɷɧɟɪɝɢɢ (8) ɪɚɜɧɚ
)2()1(
2
1
)1(
0
1
1
¦
nnnn
n
n
. (9)
6.3. ɉɨ ɨɬɧɨɲɟɧɢɸ ɤ ɤɨɨɪɞɢɧɚɬɧɵɦ ɩɟɪɟɦɟɧɧɵɦ ɩɨɬɟɧɰɢɚɥ
¸
¸
¹
·
¨
¨
©
§
Z
zy
zy
x
m
zyxU
22
),,(
22
2
2
0
(1)
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɤɜɚɞɪɚɬɢɱɧɭɸ ɮɨɪɦɭ, ɧɨ ɧɟ ɢɦɟɟɬ «ɨɫɰɢɥɥɹɬɨɪɧɨɝɨ» ɜɢɞɚ
ɢɡ-ɡɚ ɧɚɥɢɱɢɹ ɱɥɟɧɚ y
z
. ɋɞɟɥɚɟɦ ɡɚɦɟɧɭ ɩɟɪɟɦɟɧɧɵɯ, ɜ ɪɟɡɭɥɶɬɚɬɟ ɤɨɬɨɪɨɣ
U
ɛɭɞɟɬ ɫɨɞɟɪɠɚɬɶ ɨɞɧɢ ɥɢɲɶ ɤɜɚɞɪɚɬɵ ɧɨɜɵɯ ɤɨɨɪɞɢɧɚɬɧɵɯ ɩɟɪɟɦɟɧɧɵɯ.
ɐɟɥɟɫɨɨɛɪɚɡɧɨ ɩɪɢɦɟɧɢɬɶ ɨɪɬɨɝɨɧɚɥɶɧɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɤɨɨɪɞɢɧɚɬ
(ɨɬɜɟɱɚɸɳɟɟ ɧɟɤɨɬɨɪɨɦɭ ɩɨɜɨɪɨɬɭ ɤɨɨɪɞɢɧɚɬɧɨɣ ɫɢɫɬɟɦɵ); ɬɚɤɨɟ
ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɧɟ ɢɡɦɟɧɹɟɬ ɮɨɪɦɭ ɨɩɟɪɚɬɨɪɚ ɤɢɧɟɬɢɱɟɫɤɨɣ ɷɧɟɪɝɢɢ ɜ
ɭɪɚɜɧɟɧɢɢ ɒɪɟɞɢɧɝɟɪɚ.
ȼ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɦ ɩɪɢɦɟɪɟ ɬɪɟɛɭɟɦɨɟ ɩɪɟɨɛɪɚɡɨɜɚɧɢɟ ɤɨɨɪɞɢɧɚɬ
Z
Y
Xzy
x
,,,, o ɥɟɝɤɨ ɩɨɞɛɢɪɚɟɬɫɹ. Ⱦɟɣɫɬɜɢɬɟɥɶɧɨ, ɬɚɤ ɤɚɤ
, ɦɵ ɡɚɤɥɸɱɚɟɦ, ɱɬɨ
zyzy 2/)(
22
2/)(
2
zy
x
X ,
2
zy
Y
,
2
zy
Z
. (2)
ɉɟɪɟɦɟɧɧɵɟ (2) – ɷɬɨ ɤɨɨɪɞɢɧɚɬɵ ɜ ɞɟɤɚɪɬɨɜɨɣ ɫɢɫɬɟɦɟ, ɨɛɪɚɡɭɸɳɟɣɫɹ ɩɪɢ
ɩɨɜɨɪɨɬɟ ɩɟɪɜɨɧɚɱɚɥɶɧɵɯ ɞɟɤɚɪɬɨɜɵɯ ɨɫɟɣ ɧɚ ɭɝɨɥ 4
/
S ɜ ɩɥɨɫɤɨɫɬɢ . ȼ
ɧɨɜɨɣ ɫɢɫɬɟɦɟ ɤɨɨɪɞɢɧɚɬ ɩɨɬɟɧɰɢɚɥ (1) ɩɪɢɧɢɦɚɟɬ ɜɢɞ:
zy,
22
0
22
0
2
1
2
1
),,( YmXmZYXU ZZ . (3)
ɇɚɩɨɦɧɢɦ ɱɢɬɚɬɟɥɸ, ɤɚɤ ɜ ɫɥɭɱɚɟ ɤɜɚɞɪɚɬɢɱɧɨɝɨ ɩɨɬɟɧɰɢɚɥɚ ɨɛɳɟɝɨ ɜɢɞɚ
ɩɨɥɭɱɚɬɶ ɩɨɞɨɛɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɫɢɫɬɟɦɚɬɢɱɟɫɤɢɦ ɩɭɬɟɦ. ɋɤɚɥɹɪɧɚɹ
ɤɜɚɞɪɚɬɢɱɧɚɹ ɮɨɪɦɚ )ɩɪɟɞɫɬɚɜɥɹɟɬɫɹ ɜ ɜɢɞɟ,,(
321
xxxU
29
