Лыков С.Н., Гасумянц В.Э., Рыков С.А. Квантовая механика. Учебное пособие
Подождите немного. Документ загружается.


ɧɚɯɨɠɞɟɧɢɹ ɩɥɨɬɧɨɫɬɢ ɩɨɬɨɤɚ ɱɚɫɬɢɰ , ɨɬɪɚɠɚɸɳɢɯɫɹ ɨɬ ɩɨɬɟɧɰɢɚɥɶɧɨɝɨ
ɛɚɪɶɟɪɚ ɜ ɨɛɥɚɫɬɶ 1, ɫɥɟɞɭɟɬ ɜɵɛɪɚɬɶ ɭɫɥɨɜɢɟ 0
ɨɬɪ
j
3
B , ɨɡɧɚɱɚɸɳɟɟ ɨɬɫɭɬɫɬɜɢɟ
ɩɨɬɨɤɚ ɱɚɫɬɢɰ, ɧɚɩɪɚɜɥɟɧɧɨɝɨ ɤ ɛɚɪɶɟɪɭ ɢɡ ɨɛɥɚɫɬɢ 3; ɩɪɢ ɷɬɨɦ ɞɜɭɤɪɚɬɧɨɦɭ
ɜɵɪɨɠɞɟɧɢɸ ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɜɨɡɦɨɠɧɨɫɬɶ ɪɚɫɫɦɚɬɪɢɜɚɬɶ ɚɧɚɥɨɝɢɱɧɭɸ ɡɚɞɚɱɭɫ
ɭɫɥɨɜɢɟɦ 0 – ɨɛ ɨɬɪɚɠɟɧɢɢ ɱɚɫɬɢɰ ɜ ɨɛɥɚɫɬɶ 3 ɩɪɢ ɨɬɫɭɬɫɬɜɢɢ ɱɚɫɬɢɰ,
ɩɚɞɚɸɳɢɯ ɧɚ ɛɚɪɶɟɪ ɢɡ ɨɛɥɚɫɬɢ 1. ȼɫɬɪɟɱɚɸɬɫɹ ɡɚɞɚɱɢ ɢ ɞɪɭɝɨɝɨ ɬɢɩɚ. Ɍɚɤ, ɩɪɢ
ɨɩɢɫɚɧɢɢ ɩɪɨɰɟɫɫɨɜ ɜɨɡɛɭɠɞɟɧɢɹ ɱɚɫɬɢɰɵ ɢɡ ɫɨɫɬɨɹɧɢɹ ɫ ɞɢɫɤɪɟɬɧɵɦ ɭɪɨɜɧɟɦ
ɷɧɟɪɝɢɢ ɜ ɫɢɦɦɟɬɪɢɱɧɨɣ ɹɦɟ ɜ ɫɨɫɬɨɹɧɢɹ ɧɟɩɪɟɪɵɜɧɨɝɨ ɫɩɟɤɬɪɚ ɫɭɳɟɫɬɜɟɧɧɵ
ɪɟɲɟɧɢɹ, ɨɛɥɚɞɚɸɳɢɟ ɨɩɪɟɞɟɥɟɧɧɨɣ ɱɟɬɧɨɫɬɶɸ ɨɬɧɨɫɢɬɟɥɶɧɨ ɡɚɦɟɧɵ
1
A
x
x
o .
ȼ ɫɢɥɭ ɞɜɭɤɪɚɬɧɨɝɨ ɜɵɪɨɠɞɟɧɢɹ ɡɧɚɱɟɧɢɣ H , ɩɪɢɧɚɞɥɟɠɚɳɢɯ ɧɟɩɪɟɪɵɜɧɨɣ
ɱɚɫɬɢ ɷɧɟɪɝɟɬɢɱɟɫɤɨɝɨ ɫɩɟɤɬɪɚ, ɤɚɠɞɨɦɭ ɬɚɤɨɦɭ H ɦɨɠɧɨ ɫɨɩɨɫɬɚɜɢɬɶ ɨɞɧɨ
ɱɟɬɧɨɟ ()ɢ ɨɞɧɨ ɧɟɱɟɬɧɨɟ (
ɱɟɬ
\
ɧɟɱ
\ ) ɪɟɲɟɧɢɹ ɜɢɞɚ (4).
Ⱦɥɹ ɩɨɫɬɪɨɟɧɢɹ ɧɟɱɟɬɧɨɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɩɨɥɨɠɢɦ
22
BA .
ȼɨɫɩɨɥɶɡɭɟɦɫɹ ɨɛɨɡɧɚɱɟɧɢɟɦ
22
BA iC 2
/
, (8)
ɝɞɟ C – ɜɟɳɟɫɬɜɟɧɧɚɹ ɩɨɫɬɨɹɧɧɚɹ. Ɍɨɝɞɚ ɢɫɤɨɦɚɹ )(x
ɧɟɱ
\ ɜ ɨɛɥɚɫɬɢ a
x
a
ɩɪɢɦɟɬ ɜɢɞ ɜɟɳɟɫɬɜɟɧɧɨɣ ɮɭɧɤɰɢɢ . ɉɨɞɫɬɚɜɢɜ (8) ɜ ɫɨɨɬɧɨɲɟɧɢɹ (5),
(6) ɢ ɜɵɪɚɡɢɜ ɬɚɤɢɦ ɨɛɪɚɡɨɦ ɜɫɟ ɤɨɷɮɮɢɰɢɟɧɬɵ ɢ ɜ (4) ɱɟɪɟɡ
ɧɨɪɦɢɪɨɜɨɱɧɭɸ ɩɨɫɬɨɹɧɧɭɸ
xkC
2
sin
n
A
n
B
C , ɩɨɥɭɱɢɦ:
°
¯
°
®
!
\
axeAeA
axaxkC
axeAeA
x
xkixki
xkixki
ɧɟɱ
,
,sin
,
)(
11
11
*
2
*
, (9)
ɝɞɟ
)cossin(
2
2
1
2
2
1
ak
k
k
iak
C
eA
aik
. (10)
Ⱦɥɹ ɩɨɫɬɪɨɟɧɢɹ ɱɟɬɧɨɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɩɪɢɦɟɦ ɜɦɟɫɬɨ (8) ɭɫɥɨɜɢɟ
22
BA 2
/
C . (11)
Ⱦɟɣɫɬɜɭɹ ɤɚɤ ɢ ɜ ɩɪɟɞɵɞɭɳɟɦ ɫɥɭɱɚɟ, ɩɨɥɭɱɢɦ
°
¯
°
®
!
\
axeBeB
axaxkC
axeBeB
x
xkixki
xkixki
ɱɟɬ
,
,cos
,
)(
11
11
*
2
*
, (12)
10
ɝɞɟ
)sincos(
2
2
1
2
2
1
ak
k
k
iak
C
eB
aik
. (13)
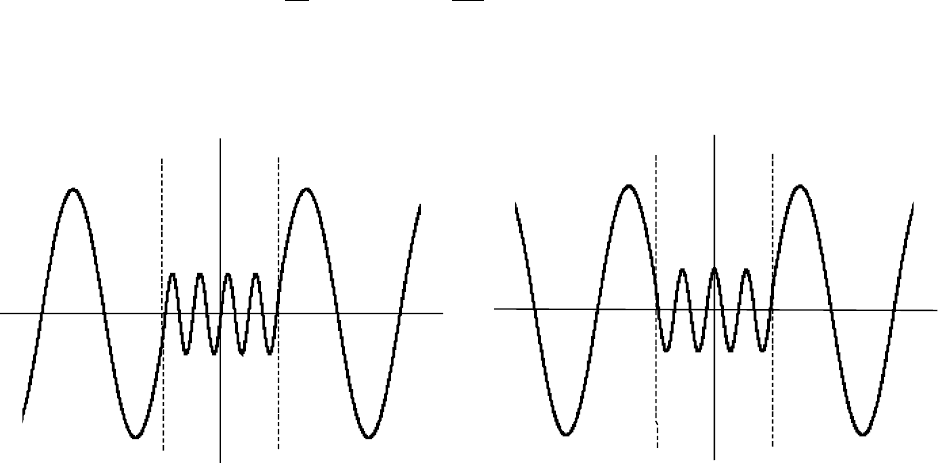
ɇɚɣɞɟɧɧɵɟ ɮɭɧɤɰɢɢ ɜɟɳɟɫɬɜɟɧɧɵ, ɢɯ ɝɪɚ
Ɋɢɫ. 5.6
Ɉɬɦɟɬɢɦ ɮɢɤɫɢɪɨɜɚɧɧɨɦ ɤɚɤɢɦ-ɥɢɛɨ ɧɨɪɦɢɪɨɜɨɱɧɵɦ ɭɫɥɨɜɢɟɦ
ɪɚɡɦɚɯɟ ɨɫɰɢɥɥɹɰɢɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɨɛɥɚɫɬɢ 2 ɡɧɚɱɟɧɢɹ ɜɨɥɧɨɜɨɣ
ɚɡɦɚɯ ɨɫɰɢɥɥɹɰɢɣ
ɮɢɤɢ ɢɡɨɛɪɚɠɟɧɵ ɧɚ ɪɢɫ. 5.6 ɢ 5.7.
Ɋɢɫ. 5.7
ɨɛɥɚɫɬɶ 1
ɱɟɬ.
<
ɨɛɥɚɫɬɶ 2
ɨɛɥɚɫɬɶ 3
x
x = a
x = -a
ɧɟɱ.
ɨɛɥɚɫɬɶ 3
ɨɛɥɚɫɬɶ 2
ɨɛɥɚɫɬɶ 1
x = a
x = -a
x
<
, ɱɬɨ ɩɪɢ
ɜɧɟ
ɮɭɧɤɰɢɢ ɜɧɭɬɪɢ ɨɛɥɚɫɬɢ 2 ɜ ɨɛɳɟɦ ɫɥɭɱɚɟ ɢɦɟɸɬ ɡɚɦɟɬɧɨ ɦɟɧɶɲɭɸ ɜɟɥɢɱɢɧɭ.
ɍɤɚɡɚɧɧɨɟ ɪɚɡɥɢɱɢɟ ɨɫɨɛɟɧɧɨ ɫɭɳɟɫɬɜɟɧɧɨ ɩɪɢ
1
k <<
2
k , ɤɨɝɞɚ ɜ (10) ɢɥɢ (13)
ɞɨɦɢɧɢɪɭɟɬ ɱɥɟɧ, ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɵɣ
12
/ kk . ɗɬɨ ɨɡɧɚɱɚɟɬ, ɱɬɨ ɩɪɢ ɦɚɥɨɣ
ɷɧɟɪɝɢɢ ( mk 2/
2
1
2
= H <<
0
U ) ɩɥɨɬɧɨɫɬɶ ɜɟɪɨɹɬɧɨɫɬɢ ɨɛɧɚɪɭɠɟɧɢɹ ɱɚɫɬɢɰɵ ɜ
ɨɛɥɚɫɬɢ ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɵ ɜ ɨɛɳɟɦ ɫɥɭ ɳɟɫɬɜɟɧɧɨ ɦɟɧɶɲɟ, ɱɟɦ ɜɧɟ ɹɦɵ.
ɋɨɨɬɜɟɬɫɬ ɚɠɟ (2) ɢ (3) ɫɥɟɞɭɟɬ, ɱɬɨ ɤɨɷɮɮɢɰɢɟɧɬ ɩɪɨɯɨɠɞɟɧɢɹ
ɱɟɪɟɡ ɨɛɥɚɫɬɶ 2 ɩɪɢ 0
1
ok ɫɬɪɟɦɢɬɫɹ ɤ ɧɭɥɸ, ɚ ɤɨɷɮɮɢɰɢɟɧɬ ɨɬɪɚɠɟɧɢɹ
ɱɚɫɬɢɰɵ ɨɬ ɫɬɟɧɨɤ ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɵ ɫɬɪɟɦɢɬɫɹ ɤ ɟɞɢɧɢɰɟ.
ɂɫɤɥɸɱɟɧɢɟ ɩɪɟɞɫɬɚɜɥɹɸɬ ɫɥɭɱɚɢ, ɜ ɤɨɬɨɪɵɯ ɩɪɨɢɡɜɨɞɧɚɹ ɜɨɥɧɨɜɨɣ
ɮɭɧɤɰɢɢ ɧɚ ɝɪɚɧɢɰɚɯ ɹɦɵ ɨɛɪɚɳɚɟɬɫɹ ɜ ɧɭɥɶ, ɬɚɤ ɱɬɨ ɪ
ɱɚɟ ɫɭ
ɜɟɧɧɨ, ɢɡ ɜɵɪ ɧɢɣ
ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɨɤɚɡɵɜɚɟɬɫɹ ɨɞɧɢɦ ɢ ɬɟɦ ɠɟ ɜɨ ɜɫɟɯ ɨɛɥɚɫɬɹɯ ɨɫɢ
x
. ȼ ɷɬɢɯ
ɫɥɭɱɚɹɯ ɱɥɟɧ ɫ
12
/ kk ɜ (10) ɢɥɢ (13) ɪɚɜɟɧ ɧɭɥɸ. Ⱦɥɹ ɫɨɫɬɨɹɧɢɹ ɫ ɧɟɱɟɬɧɨɣ
ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɟɣ ɬɚɤ ɩɪɨɢɫɯɨɞɢɬ ɩɪɢ ɜɵɩɨɥɧɟɧɢɢ ɭɫɥɨɜɢɹ
0cos
2
ak , (14)
ɬɨ ɟɫɬɶ ɩɪɢ ɭɫɥɨɜɢɢ, ɱɬɨ ɧɚ ɞɥɢɧɟ
ɞɟɛɪɨɣɥɟɜɫɤɨɣ ɞɥɢɧɵ ɜɨɥɧɵ /2/ k
ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɵ ad 2 ɩɨɥɨɜɢɧɚ
2
S O ɭɤɥɚɞɵɜɚɟɬɫɹ ɧɟɱɟɬɧɨɟ ɪɚɡ. Ⱦɥɹ
ɚɧɫ» ɧ
ɱɢɫɥɨ
ɫɨɫɬɨɹɧɢɹ ɫ ɱɟɬɧɨɣ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɟɣ ɩɨɞɨɛɧɵɣ «ɪɟɡɨɧ ɚɫɬɭɩɚɟɬ ɜ
ɫɥɭɱɚɟ
11
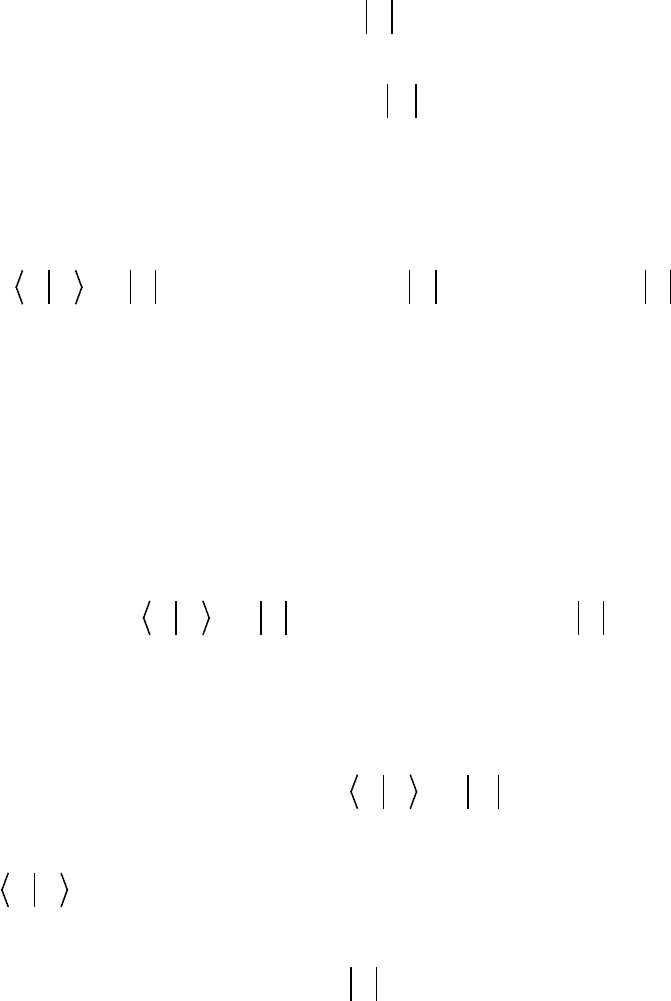
0sin
2
ak , (15)
ɬɨ ɟɫɬɶ ɩɪɢ ɭɫɥɨɜɢɢ, ɱɬɨ ɧɚ ɞɥɢɧɟ ɹɦɵ ɜɟɥɢɱɢɧɚ 2
/
O ɭɤɥɚɞɵɜɚɟɬɫɹ ɱɟɬɧɨɟ
ɱɢɫɥɨ ɪɚɡ. ɂɦɟɧɧɨ ɜ ɫɥɭɱɚɹɯ (14) ɢ (15) ɩɪɨɯɨɠɞɟɧɢɹ
ɨɜ
ɢ, ɨɬɧɨɫɹɳɟɣɫɹ ɤ ɧɟɩɪɟɪɵɜɧɨɦɭ ɷɧɟɪɝɟɬɢɱɟɫɤɨɦɭ
ɤɨɷɮɮɢɰɢɟɧɬ D
ɫɬɚɧɨɜɢɬɫɹ ɪɚɜɧɵɦ ɟɞɢɧɢɰɟ.
ȼ ɡɚɜɟɪɲɟɧɢɟ ɪɚɫɫɦɨɬɪɢɦ ɧɟɤɨɬɨɪɵɟ ɢɡ ɜɨɡɦɨɠɧɵɯ ɫɩɨɫɨɛ
ɧɨɪɦɢɪɨɜɤɢ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢ
ɫɩɟɤɬɪɭ.
Ɉɛɨɡɧɚɱɢɜ ɩɨɫɪɟɞɫɬɜɨɦ G ɮɚɡɭ ɤɨɦɩɥɟɤɫɧɨɣ ɜɟɥɢɱɢɧɵ (10), ɡɚɩɢɲɟɦ
ɧɟɱɟɬɧɭɸ ɜɨɥɧɨɜɭɸ ɮɭɧɤɰɢɸ (9) ɜ ɜɢɞɟ
°
¯
°
®
xkA (cos2
1
!G
G
\
axxkA
axaxkC
ax
x
ɧɟɱ
),(cos2
,sin
,)
)(
1
2
. (16)
ɇɨɪɦɢɪɨɜɨɱɧɵɣ ɢɧɬɟɝɪɚɥ ɞɥɹ )(x
ɧɟɱ
\ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɫɭɦɦɭ ɜɤɥɚɞɨɜ ɨɬ
ɬɪɟɯ ɨɛɥɚɫɬɟɣ ɨɫɢ
x
:
\\
³
f
G
xk )(cos
1
2
a
dxA4
2
³
a
a
xkdxC
2
2
2
sin
³
f
G
a
xkdxA )(cos4
1
2
2
. (17)
Ⱦɜɚ ɢɡ ɬɪɟɯ ɭɤɚɡɚɧɧɵɯ ɜɤɥɚɞɨɜ ɪɚɫɯɨɞɹɬɫɹ ɩɪɢ rfo
x
. ɉɪɟɧɟɛɪɟɝɚɹ ɤɨɧɟɱɧɵɦ
ɜɤɥɚɞɨɦ ɨɛɥɚɫɬɢ 2 ɩɨ ɫɪɚɜɧɟɧɢɸ ɫ ɛɟɫɤɨɧɟɱɧɨ ɜɤɥɚɞɚɦɢ ɨɛɥɚɫɬɟɣ 1, ɛɨɥɶɲɢɦɢ
3 ɢ ɫɱɢɬɚɹ, ɱɬɨ ɜɨɥɧɨɜɵɟ ɮɭɧɤɰɢɢ ɪɚɫɫɦɚɬɪɢɜɚɸɬɫɹ ɧɚ ɢɧɬɟɪɜɚɥɟ
2
/
2
/
L
x
L
, ɝɞɟ
L
– ɫɬɪɟɦɹɳɚɹɫɹ ɤ ɛɟɫɤɨɧɟɱɧɨɫɬɢ ɞɥɢɧɚ ɫɭɦɦɚɪɧɨɝɨ
ɢɧɬɟɪɜɚɥɚ ɢɧɬɟɝɪɢɪɨɜɚɧɢɹ ɜ (17), ɦɨɠɧɨ ɡ ɩɢɫɚɬɶ ɜɦɟɫɬɨ ɩɪɚɜɨɣ ɱɚɫɬɢ (17)
ɪɚɠɟɧ ɟ
ɚ
ɛɨɥɟɟ ɩɪɨɫɬɨɟ ɜɵ ɢ
³
G
2/
0
1
2
2
)(cos4
L
xkdxA .
³
G
0
2
/
1
2
2
4 A )(cos
L
xkdx \\
Ɂɚɦɟɧɢɜ ɜ ɤɚɠɞɨɦ ɢɡ ɷɬɢɯ ɢɧɬɟɝɪɚɥɨɜ ɤɜɚɞɪɚɬ ɤɨɫɢɧɭɫɚ ɟɝɨ ɫɪɟɞɧɢɦ ɡɧɚɱɟɧɢɟɦ,
ɪɚɜɧɵɦ 2
/
1,ɩɨɥɭɱɢɦ
\\
LA
2
2
. (18)
Ɉɞɢɧ ɢɡ ɜɨɡɦɨɠɧɵɯ ɫɩɨɫɨɛɨɜ ɧɨɪɦɢɪɨɜɤɢ ɫɜɨɞɢɬɫɹ ɤ ɧɚɥɨɠɟɧɢɸ ɭɫɥɨɜɢɹ
\\ 1; ɷɬɨ ɧɨɪɦɢɪɨɜɤɚ ɧɚ ɟɞɢɧɢɰɭ ɜ ɢɧɬɟɪɜɚɥɟ
L
. ɋ ɭɱɟɬɨɦ (18) ɭɤɚɡɚɧɧɨɟ
ɭɫɥɨɜɢɟ ɞɚɟɬ:
LA 2/1
2
. (19)
12

ɠɢɬ ɧɨɪɦɢɪɨɜɨɱɧɵɣ ɩɚɪɚɦɟɬɪ
L
(ɨɧɚȼ ɷɬɨɦ ɫɥɭɱɚɟ ɜɨɥɧɨɜɚɹ ɮɭɧɤɰɢɹ ɫɨɞɟɪ
ɩɪɨɩɨɪɰɢɨɧɚɥɶɧɚ
L
/
1),ɨɞɧɚɤɨ ɜ ɨɤɨɧɱɚɬɟɥɶɧɵɯ ɜɵɪɚɠɟɧɢɹɯ ɞɥɹ ,ɜɟɥɢɱɢɧ
ɢɦɟɸɳɢɯ ɧɟɩɨɫɪɟɞɫɬɜɟɧɧɵɣ ɮɢɡɢɱɟɫɤɢɣ ɫɦɵɫɥ, ɡɚɜɢɫɢɦɨɫɬɶ ɨɬ ɩɪɨɢɡɜɨɥɶɧɨɝɨ
ɩɚɪɚɦɟɬɪɚ
L
ɞɨɥɠ ɟɡɚɬɶ.
Ȼɨɥɟɟ ɩɪɟɞɩɨɱɬɢɬɟɥɶɧɨɣ ɦɨɠɟɬ ɛɵɬɶ ɧɨɪɦɢɪɨɜɤɚ ɧɚ ɞɟɥɶɬɚ-ɮɭɧɤɰɢɸ ɨɬ
ɜɨɥɧɨɜɨɝɨ ɱɢɫɥɚ
1
k :
ɧɚ ɢɫɱ
f
c
c
GS \\ )(2)()(
11
*
11
kkxxdx
kk
. (20)
Ɂɞɟɫɶ ɜɨɥɧɨɜɵɦ ɮɭɧɤɰɢɹɦ ɩɪɢɩɢɫɚɧ ɢɧɞɟɤɫ ɩɨɫɤɨɥɶɤɭ ɪ ɫɦɚɬ ɢɜɚɟ
ɫɨɫɬɨɹɧɢɹ ɯɚɪɚɤɬɟɪɢɡɭɸɬɫɹ ɨɩɪɟɞɟɥɟɧɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɜɨɥɧɨɜɨɝɨ ɱɢɫɥɚ
. (21)
ɉɪɢ ɩɪɚɜɚɹ ɫɬɨɪɨɧɚ ɪɚɜɟɧɫɬɜɚ (20) ɨɛɪɚɳ
ɜɡɚɢɦɧɨɣ ɨɪɬɨɝɨɧɚɥɶɧɨɫɬɶɸ ɮɭɧɤɰɢɣ
³
f
1
k , ɚɫ ɪ ɦɵɟ
1
k
ɧɚɪɹɞɭ ɫ ɨɩɪɟɞɟɥɟɧɧɵɦɢ ɡɧɚɱɟɧɢɹɦɢ ɷɧɟɪɝɢɢ:
mk 2/
2
1
2
= H
11
kk z
c
ɚɟɬɫɹ ɜ ɧɭɥɶ, ɱɬɨ ɨɛɭɫɥɨɜɥɟɧɨ
1
k
c
\ ɢ
1
k
\ . ɉɪɢ
11
kk
c
ɢɧɬɟɝɪɚɥ ɜ ɥɟɜɨɣ
(20)
ɜɚɹ ɫɬɶ ɬɜɚ (20
ɱɚɫɬɢ ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɧɨɪɦɢɪɨɜɨɱɧɵɣ ɢɧɬɟɝɪɚɥ, ɢ ɟɝɨ ɦɨɠɧɨ
ɨɬɨɠɞɟɫɬɜɢɬɶ ɫ ɜɵɪɚɠɟɧɢɟɦ (18), ɚ ɩɪɚ ɱɚ ɪɚɜɟɧɫ ) ɟɫɬɶ
L
GS )0(2
– ɫɨɝɥɚɫɧɨ ɩɨɹɫɧɟɧɢɹɦ ɤ ɮɨɪɦɭɥɟ (10) ɜ ɡɚɞɚɱɟ 4.3. Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɞɥɹ
ɜɵɩɨɥɧɟɧɢɹ ɧɨɪɦɢɪɨɜɨɱɧɨɝɨ ɭɫɥɨɜɢɹ (20) ɫɥɟɞɭɟɬ ɩɪɢɧɹɬɶ, ɱɬɨ
LLA2
ɟɫɬɶ
2
, ɬɨ
2/1
2
A
. (22)
Ɋɚɫɫɦɨɬɪɢɦ ɬɚɤɠɟ ɭɫɥɨɜɢɟ ɧɨɪɦɢɪɨɜɤɢ
11
)
Ɋɚɡɥɨɠɢɦ ɜ ɚɪɝɭɦɟɧɬɟ ɞɟɥɶɬɚ-ɮɭɧɤɰɢɢ ɜ ɪɹɞ ɩɨ ɫɬɟɩ
ɧɚ ɞɟɥɶɬɚ-ɮɭɧɤɰɢɸ ɨɬ ɷɧɟɪɝɢɢ:
³
f
c
H
c
HG \\ )()()(
*
xxdx
kk
. (23
f
ɟɧɹɦ
11
kk
c
,H
...)(
11
c
H
H
c
H kk
d
,
1
11
c
dk
kk
ɢ ɭɞɟɪɠɢɦ ɬɨɥɶɤɨ ɩɟɪɜɵɟ ɞɜɚ ɱɥɟɧɚ ɪɹɞɚ. ɉɨɥɭɱɚɟɦ
)(
/
1
)()(
11
kk
d
¸
¸
·
¨
¨
§
c
H
G H
c
HG
11
11
kk
dkddk
c
G
H
¹©
,
13

ɬɚɤ ɱɬɨ ɭɫɥɨɜɢɟ (23) ɩɪɢɧɢɦɚɟɬ ɜɢɞ
³
f
f
11
kk
c
c
G \\ )()()(
11
1
2
*
kk
k
m
xxdx
=
. (24)
ɋɪɚɜɧɢɜɚɹ (24) ɫ (20), ɜɢɞɢɦ, ɱɬɨ ɞɥɹ ɩɟɪɟɯɨɞɚ ɤ (24) ɞɨɫɬɚɬɨɱɧɨ ɩɪɚɜɭɸ
ɫɬɨɪɨɧɭ ɪɚɜɟɧɫɬɜɚ (22), ɩɨɥɭɱɟɧɧɨɝɨ ɢɡ ɧɨɪɦɢɪɨɜɨɱɧɨɝɨ ɭɫɥɨɜɢɹ (20),
ɭɦɧɨɠɢɬɶ ɧɚ Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɧɨɪɦɢɪɨɜɤɚ ɧɚ
1
2
2/ km =S . G-ɮɭɧɤɰɢɸ ɨɬ ɷɧɟɪɝɢɢ
ɢɦɟɟɬ ɦɟɫɬɨ ɩɪɢ
1
2
2
2 k
m
A
=S
. (25)
ɉɨɫɥɟ ɬɨɝɨ ɤɚɤ ɞɥɹ
2
A
ɜɟɳɟɫɬɜɟɧɧɵɣ
ɛɭɞɟɬ ɩɪɢɧɹɬɨ ɨɞɧɨ ɢɡ ɧɨɪɦɢɪɨɜɨɱɧɵɯ ɡɧɚɱɟɧɢɣ
(19), (22) ɢɥɢ (25), ɤɨɷɮɮɢɰɢɟɧɬ C ɜ (9) ɨɩɪɟɞɟɥɢɬɫɹ ɜ
ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (10) ɪɚɜɟɧɫɬɜɨɦ
akkakk
kA
C
2222
1
2
1
2
2
cossin
4
(26)
222
.
Ⱥɧɚɥɨɝɢɱɧɨ ɩɪɨɢɡɜɨɞɢɬɫɹ ɧɨɪɦɢɪɨɜɤɚ ɱɟɬɧɨɝɨ ɪɟɲɟɧɢɹ (12). Ɉɞɧɨ ɢɡ ɡɧɚɱɟɧɢɣ
(19), (22) ɢɥɢ (25) ɜ ɷɬɨɦ ɫɥɭɱɚɟ ɫɥɟɞɭɟɬ ɩɪɢɩɢɫɚɬɶ ɜɟɥɢɱɢɧɟ
2
B
ɱɟɝɨ, ɩɨɫɥɟ
ɤɨɷɮɮɢɰɢɟɧɬ C ɜ (12) ɨɩɪɟɞɟɥɢɬɫɹ ɜ ɫɨɨɬɜɟɬɫɬɜɢɢ ɫ (13) ɪɚɜɟɧɫɬɜɨɦ
akkakk
kB
C
2
22
22
22
1
2
1
2
2
sincos
4
. (27)
5.4. ɉɪɢ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ ɒɪɟɞɢɧɝɟɪɚ ɢɦɟɟɬ ɜɢɞ
!
\
233
111
,
,
xxeBeA
xxeBeA
xkixki
xkixki
(1)
ɝɞɟ
WH
°
¯
°
®
NN
2122
,)( xxxeBeAx
xx
,
2
/2 =H mk ,
2
/)(2 =H N Wm . (2)
ɨɥɶɤɭ ɧɚ ɜɨɥɧɨɜɭɸ ɮɭɧɤɰɢɸ ɡɞɟɫɶ ɧɚɥɚɝɚɸɬɫɹ ɬɟ ɠɟ ɭɫɥɨɜɢɹ
ɧɟɩɪɟɪɵɜɧɨɫɬɢ, ɱɬɨ ɢ ɜ ɡɚɞɚɱɟ 5, ɜɨɫɩɨɥɶɡɨɜɚɬɶɫɹ ɮɨɪɦɭɥɚɦɢ (5)–
ɭɤɚɡɚɧɧɨɣ ɡɚɞɚɱɢ, ɩɨɥɨɠɢɜ ɜ ɷɬɢ ɪɦɭɥɚɯ
ɉɨɫɤ
.2 ɦɨɠɧɨ (9)
ɯɮɨ
kk
1
, N ik
2
. (3)
14

Ɍɚɤ, ɞɥɹ ɦɚɬ ɢɰɵ «ɩɟɪɟɧɨɫɚ» ɢɡ ɬɨɱɤɢ 0
1
ɪ x ɜ ɨɱɤɭ 0
2
ɬ x ɩ ɥɭɱɢɦɨ
¸
¸
¹
¨
¨
©
N
N
N
N
d
ki
d
ki
ch
2
sh
2
¸
¸
Nki2
2
. (4)
¸
·
¨
¨
N
NN
N
N
N
d
kk
d
k
ki
t
sh
sh
2
ˆ
222
22
ɂɫɤɨɦɚɹ ɜɟɪɨɹɬɧɨɫɬɶ ɩɪɨɯɨɠɞɟɧɢɹ ɱɚɫɬɢɰɵ ɩɪɢɧɢɦɚɟɬ ɜɢɞ:
¨
§
NN
N
dd
k
chsh
22
D
1
2
22
222
sh
4
)(
1
¸
¸
¹
·
¨
¨
©
§
N
N
N
d
k
k
D . (5)
ɉɪɨɧɢɤɧɨɜɟɧɢɟ ɱɚɫɬɢɰɵ ɫ ɷɧɟɪɝɢɟɣ
H ɱɟɪ ɩɨɬɟɧɰɢɚɥɶɧɵɣɟɡ ɛɚɪɶɟɪ ɩɪɢ
ɭɫɥɨɜɢɢ ɧɚɡɵɜɚɟɬɫɹ ɬɭɧɧɟɥɶɧɵɦ ɷɮɮɟɤɬɨɦ. ɂɡ (5) ɫɥɟɞɭɟɬ, ɱɬɨ ɜ ɫɥɭɱɚɟ
ɞɨɫɬɚɬɨɱɧɨ ɲɢɪɨɤɨɝɨ ɢɥɢ ɜɵɫɨɤɨɝɨ ɛɚɪɶɟɪɚ, ɤɨɝɞɚ
ɜɟɪɨɹɬɧɨɫɬɶ ɬɭɧɧɟɥɢɪɨɜɚɧɢɹ ɦɚɥɚ ɢ ɷɤɫ
ɪɨɫɬɨɦ ɩɚɪɚɦɟɬɪɚ :
W
WH
ɜɵɩɨɥɧɹɟɬɫɹ ɧɟɪɚɜɟɧɫɬɜɨ
ɩɨɧɟɧɰɢɚɥɶɧɨ ɭɛɵɜɚɟɬ ɫ1!!Nd , D
dN
d
e
k
k
D
N
N
N
|
2
222
22
)(
16
. (6)
5.5. ȼɨɫɩɨɥ ɟɦɫɹ ɦɟɬɨɞɨɦ ɩɟɪɟɧɨɫɚ (ɫɦ. ɩɪɟɞɵɞɭɳɢɟ
ɩɪɢɦɟɪɵ, ɧɚɱɢɧɚɹ
ɶɡɭ ɦɚɬɪɢɰɵ
ɫ ɡɚɞɚɱɢ 5.1). Ɉɛɨɡɧɚɱɢɦ ɩɨɤɚɡɚɧɧɵɟ ɧɚ ɪɢɫ.5.5 ɢɧɬɟɪɜɚɥɵ
),( ) ɢ ()ɤɚɤ(
10
, xx
21
, xx
32
, xxn-, )1( n - ɢ ( n )2-ɨɛɥɚɫɬɢ ɨɫɢ
x
. Ɍɨɝɞɚ, ɜ ɫɢɥɭ
ɧɟɩɪɟɪɵɜɧɨɫɬɢ ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɢ ɟɟ ɩɪɨɢɡɜɨɞɧɨɣ ɧɚ ɝɪɚɧɢɰɚɯ ɨɛɥɚɫɬɟɣ,
ɨɥɠɧɨ ɢɦɟɬɶ ɦɟɫɬɨ ɪɚɜɟɧɫɬɜɨ:
¹©
221
2
b
T
b
nn
ɨɛɥɚɫɬɢ ɮɨɪɦɭɥɚɦ (2) ɡɚɞɚɱɢ 5.1, – ɷɥɟɦɟɧɬɵ ɭɧɢɦɨɞɭɥɹɪɧɨɣ
ɦɚɬɪɢɰɵ
ɞ
¸
¸
¹
·
¨
¨
§
¸
¸
·
¨
¨
§
¸
¸
¹
·
¨
¨
©
§
)(
)(
)(
)(
1
1
2
1211
3
32
x
xa
T
TT
x
xa
nn
. (1)
Ɂɞɟɫɶ
n
a ɢ
n
b – ɮɭɧɤɰɢɢ, ɫɜɹɡɚɧɧɵɟ ɫ ɪɟɲɟɧɢɟɦ ɭɪɚɜɧɟɧɢɹ ɒɪɟɞɢɧɝɟɪɚ ɜ
©
n ɫɨɝɥɚɫɧɨ
jj
T
c
T
ˆ
, ɢɦɟɸɳɟɣ ɜɢɞ
e
T
bki
ˆ
0
ˆ
¸
t
e
bki
0
¸
¹
·
¨
¨
©
§
, (2)
t
ˆ
– ɦɚɬɪɢɰɚ ɢɡ ɮɨɪɦɭɥɵ (4)
0
1
x ɜ ɬ ɱɤɭ 0
2
x . Ⱦɢɚ
ɡɚɞɚɱɢ 5.4, ɫɨɨɬɜɟɬɫɬɜɭɸɳɚɹ «ɩɟɪɟɧɨɫɭ» ɢɡ ɬɨɱɤɢ
ɨ ɝɨɧɚɥɶɧɚɹ ɦɚɬɪɢɰɚ ɜ (2) ɫɨɩɨɫɬɚɜɥɟɧɚ ɩɟɪɟɧɨɫɭ ɢɡ
ɜ , ɬɚɤ ɱɬɨ ɦɚɬɪɢɰɚɬɨɱɤɢ 0
2
x ɬɨɱɤɭ 0
3
x
T
ˆ
ɨɩɢɫɵɜɚɟɬ ɢɡɦɟɧɟɧɢɟ ɡɧɚɱɟɧɢɣ
15
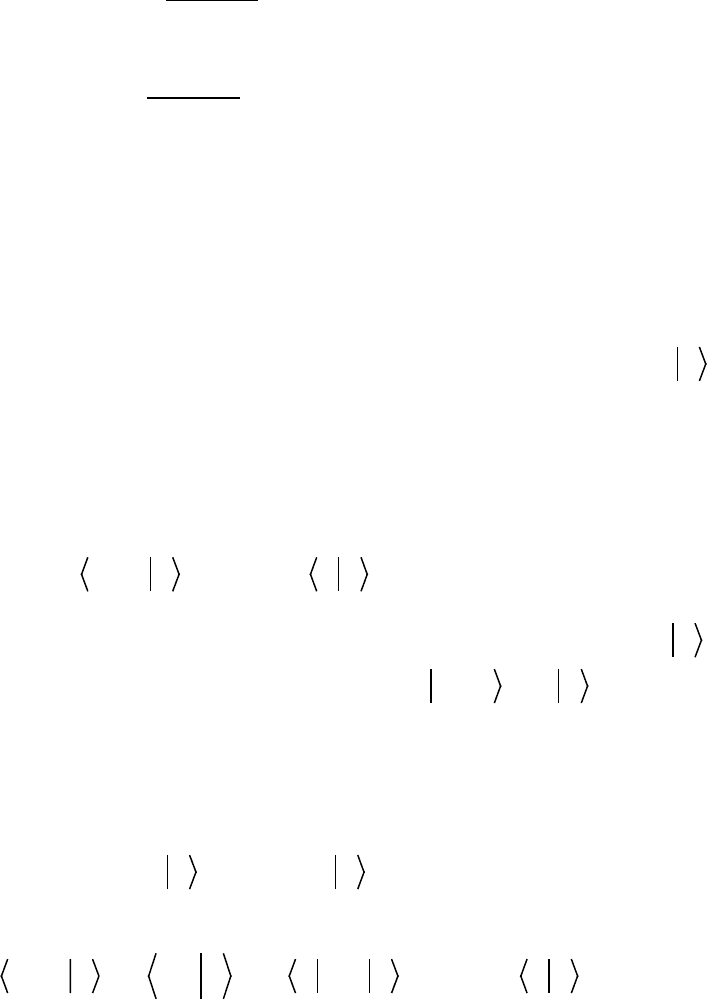
ɜɨɥɧɨɜɨɣ ɮɭɧɤɰɢɢ ɩɪɢ ɢɡɦɟɧɟɧɢɢ
x
ɧɚ ɜɟɥɢɱɢɧɭ, ɪɚɜɧɭɸ ɩɟɪɢɨɞɭ
ɩɨɬɟɧɰɢɚɥɚ
a
)(
x
U
. ȼɵɩɨɥɧɢɜ ɭɤɚɡɚɧɧɨɟ ɜ (2) ɩɟɪɟɦɧɨɠɟɧɢɟ ɦɚɬɪɢɰ, ɩɨɥɭɱɢɦ:
ded
ki
k
eT
bkibki
NN
N
N
chsh
2
11
, (3)
22
d
ki
k
eT
bk
N
N
N
sh
2
22
12
,(4)
*
i
, (5)
, (
ɝɞɟ
1221
TT
*
1122
TT 6)
k ɢ ɫɜɹɡɚɧɵ ɫ ɷɧɟɪɝɢɟɣ ɮɨɪɦɭɥɚɦɢ (2) ɡɚɞɚɱɢ 5.4.
ɋɥɟɞɭɟɬ ɨɠɢɞɚɬɶ, ɱɬɨ ɜ ɫɢɥɭ ɬɪɚɧɫɥɹ
ɫɨɫɬɨɹɧɢɹɦɢ ɱɚɫɬɢɰɵ ɜ ɩɟɪɢɨɞɢɱɟɫɤɨɦ ɩɨɥɟ ɹɜɥɹɸɬɫɹ ɫɨɫɬɨɹɧɢɹ
N H
ɰɢɨɧɧɨɣ ɫɢɦɦɟɬɪɢɢ ɫɬɚɰɢɨɧɚɪɧɵɦɢ
q ɫ
ɨɩɪɟɞɟɥɟɧɧɵɦ ɤɜɚɡɢɢɦɩɭ
ɩɪɟɞɫɬɚɜɥɹɸɬɫɹ ɧɟɤɨɬɨɪɨɣ ɮɭɧɤɰɢɟɣ
ɥɶɫɨɦ q , ɚ ɞɨɩɭɫɬɢɦɵɟ ɡɧɚɱɟɧɢɹ ɷɧɟɪɝɢɢ
)(qH , ɩɟɪɢɨɞɢɱɟɫɤɨɣ ɫ ɩɟɪɢɨɞɨɦ a
/
2 =S .
ɉɨɞɨɛɧɚɹ ɤɚɪɬɢɧɚ ɛɵɥɚ ɪɚ
, ɱɬɨ
ɫɫɦɨɬɪɟɧɚ ɧɚɦɢ ɜ ɡɚɞɚɱɟ 3.8. Ɉɫɧɨɜɵɜɚɹɫɶ ɧɚ ɬɨɦ
ɪɚɫɫɦɨɬɪɟɧɢɢ ɩɨɤɚɠɟɦ ɬɟɩɟɪɶ
qxeqax
aqi =/
.(7)
ɋɤɚɥɹɪɧɨ ɭɦɧɨɠɢɜ ɜɟɤɬɨɪ ɫɨɫɬɨɹɧ ɫ ɩɪ ɞɟɥɟɧɧɵɦ ɤɜɚɡɢɢɦɩɭɥɶɫɨɦɢɹ ɨ ɟ
q ɧɚ
ɜɟɤɬɨɪ ɫɨɫɬɨɹɧɢɹ ɫ ɨɩɪɟɞɟɥɟɧɧɨɣ ɞɢɧɚɬɨɣɤɨɨɪ
xTax
1
ˆ
, ɝɞɟ
1
ɭɧɢɬɚɪɧɵɣ ɨɩɟɪɚɬɨɪ ɩɟɪɟɧɨɫɚ ɤɜɚɧɬɨɜɵɯ ɫɨɫɬɨɹɧɢɣ ɧɚ ɪɚɫɫɬɨɹɧɢɟ
a
–
ˆ
T
x
' , ɢ
ɭɱɢɬɵɜɚɹ, ɱɬɨ ɫɨɫɬɨɹɧɢɹ ɫ ɨɩɪɟɞɟɥɟɧɧɵɦ ɤɜɚɡɢɢɦɩɭɥɶɫɨɦ
ɫɨɛɫɬɜɟɧɧɵɦɢ ɞɥɹ ɨɩɟɪɚɬɨɪɚ
ɹɜɥɹɸɬɫɹ
1
ˆ
T ,
qeqT
aqi =/
1
ˆ
,
ɩɨɥɭɱɚɟɦ
qxTqax
1
ˆ
qxeqTx
aqi =/1
1
ˆ
.
Ɍɚɤɢɦ ɨɛɪɚɡɨɦ, ɫɩɪɚɜɟɞɥɢɜɨ ɫ ɨɬ
ɋɨɝɥɚɫɧɨ ɷɬɨɦɭ ɫɨɨɬɧɨɲɟɧɢɸ
ɨ ɧɨɲɟɧɢɟ (7).
ɜɨɥɧɨɜɚɹ ɮɭɧɤɰɢɹ )(
x
q
\ ɫɨɫɬɨɹɧɢɹ ɫ
ɨɩɪɟɞɟɥɟɧɧɵɦ ɤɜɚɡɢɢɦɩɭɥɶɫɨɦ ɩɪɢ ɢɡɦɟɧɟɧɢɢ ɤɨɨɪɞɢɧɚɬɵ
x
ɧɚ ɜɟɥɢɱɢɧɭ,
ɪɚɜɧɭɸ ɩɟɪɢɨɞɭ ɬɪɚɧɫɥɹɰɢɨɧɧɨɣ ɫɢɦɦɟɬɪɢɢ ɩɪɢɨɛɪɟɬɚɟɬ ɮɚɡɨɜɵɣ
a ,
)
/
(exp =iqaɦɧɨɠɢɬɟɥɶ
)()(
/
xeax
q
aqi
q
\ \
=
. (8)
16

Ɉɬɫɸɞɚ ɫɥɟɞɭɟɬ, ɱɬɨ
=/
)()(
xqi
qq
exux \ ,
ɝɞɟ )(
xu
q
– ɩɟɪɢɨɞɢɱɟɫɤɚɹ ɮɭɧɤɰɢɹ ɤɨɨɪɞɢɧɚɬɵ
x
ɫ ɩɟɪɢɨɞɨɦ a . ɗɬɨ
ɭɬɜɟɪɠɞɟɧɢɟ (ɢ ɟɝɨ ɨɛɨɛɳɟɧɢɹ ɧɚ ɫɥɭɱɚɢ ɞɜɭɦɟɪɧɵɯ ɢɥɢ ɬɪɟɯɦɟɪɧɵɯ ɫɢɫɬɟɦ,
ɩɨɞɪɨɛɧɨ ɪɚɫɫɦɚɬɪɢɜɚɟɦɵɟ ɜ ɤɭɪɫɟ ɤɜɚɧɬɨɜɨɣ ɬɟɨɪɢɢ ɬ
ɬɟɨɪɟɦɨɣ Ȼɥɨɯɚ.
ɜɟɥɢɱɢɧɵ ɢ ɜ ɥɟɜɨɣ ɫɬɨɪɨɧɟ ɪɚɜɟɧɫɬɜɚ
(1) ɞɨɥɠɧɵ ɫɨɜɩɚɞɚɬɶ ɫ ɭɦɧɨɠɟɧɧɵɦɢ ɧɚ ɜɟɥɢɱɢɧɚɦɢ ɢ
, ɢ ɭɞɨɜɥɟɬɜɨɪɹɸɬ ɫɢɫɬɟɦɟ ɨɞɧɨɪɨɞɧɵɯ ɥɢɧɟɣɧɵɯ
¸
¸
¹
¨
¨
©
¸
¸
¹
¨
¨
©
0
/
2221
12
n
aqi
b
eTT
T
=
. (10)
ɍɫɥɨɜɢɟ ɫɭɳɟɫɬɜɨɜɚɧɢɹ ɧɟɬɪɢɜɢɚɥɶɧɨɝɨ ɪɟɲɟɧɢɹ ɬɚɤɨɣ ɫɢɫɬɟɦɵ ɢɦɟɟɬ ɜɢɞ:
11
¸
¸
¹
¨
¨
©
§
=aqi
eTT
T
,
ɢɥɢ, ɫ ɭɱɟɬɨɦ ɭɧɢɦɨɞɭɥɹɪɧɨɫɬɢ
ɜɟɪɞɨɝɨ ɬɟɥɚ) ɧɚɡɵɜɚɸɬ
)(
32
xa
n
)(
32
xb
n
=/aqi
e )(
1
xa
n
)(
1
xb
n
:
ȼɫɥɟɞɫɬɜɢɟ (8)
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
¸
¸
¹
·
¨
¨
©
§
n
n
iqa
n
n
b
a
e
b
a
TT
TT
=/
2221
1211
. (9)
Ⱦɪɭɝɢɦɢ ɫɥɨɜɚɦɢ
nn
ɭɪɚɜɧɟɧɢɣ
§
·§
·§
0
/
11
n
aqi
a
eT
=
ab
¸
¸
¹
·
¨
¨
©
0det
/
2221
12
/
·
=
aqi
Te
T
ˆ
-ɦɚɬɪɢɰɵ 1(
21122211
TTTT ),
01)(
/
2211
/2
== aqiaqi
eTTe . (11)
Ɋɚɡɞɟɥɢɜ ɨɛɟ ɫɬɨɪɨɧɵ ɭɪɚɜɧɟɧɢɹ (11) ɧɚ , ɩɨɥɭɱɚɟɦ:
=/aqi
e
)/(cos)(
2
ɗɬɨ ɢ ɟɫɬɶ ɢɫɤɨɦɨɟ ɭɪɚɜɧɟɧɢɟ ɞɥ )(
q
1
2211
=qaTT . (12)
ɹ
H ; ɟɝɨ ɦɨ ɜ ɜɢɞɟɠɧɨ ɩɪɟɞɫɬɚɜɢɬɶ
)
/
(cos)( =qa
F
H , (13)
ɝɞɟ, ɫ ɭɱɟɬɨɦ (3) ɢ (6),
{H )(
2
1
)(
2211
TTF dkbdkb
k
k
NN
N
N
chcosshsin
2
22
, (14)
17
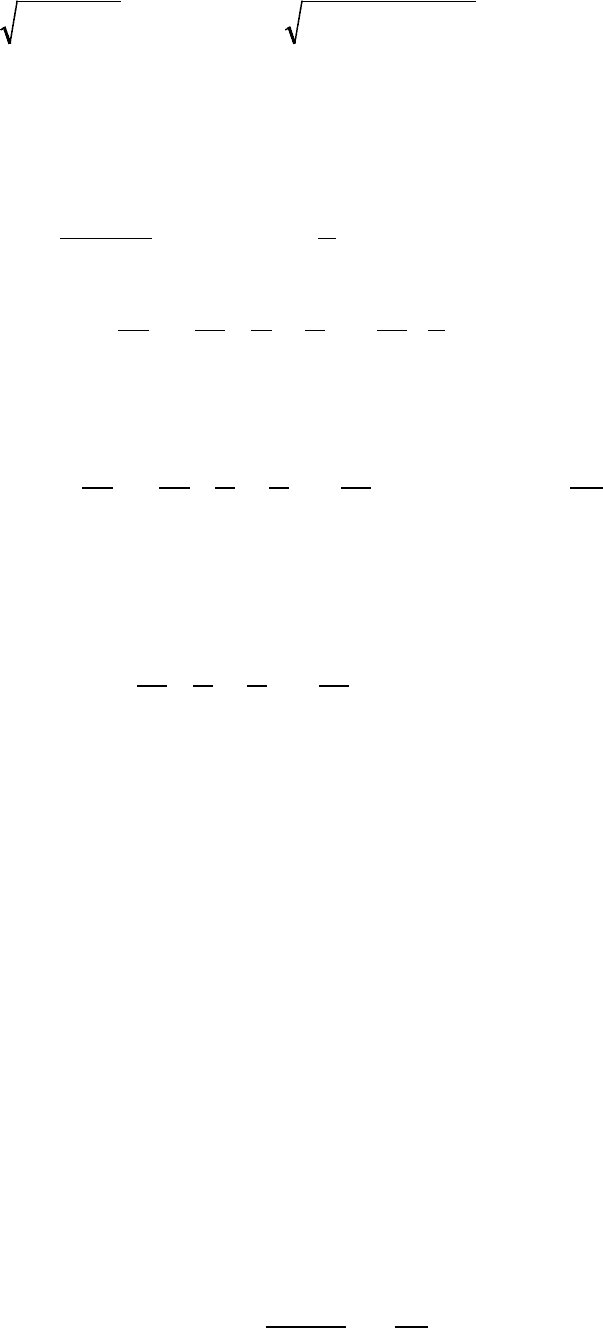
2
/2 =H mk ,
2
/)(2 =HWm . N (15)
ɏɚɪɚɤɬɟɪ ɪɟɲɟɧɢɣ ɭɪɚɜɧɟɧɢɹ (13) ɫɪɚɜɧɢɬɟɥɶɧɨ
ɧɨ ɲɢɪɨɤɢɦɢ ɛɚɪɶɟɪɚɦɢ, ɤɨɝɞɚ
ɥɟɝɤɨ ɩɨɹɫɧɢɬɶ ɜ ɫɥɭɱɚɟ
1
!!Nd .ɩɨɬɟɧɰɢɚɥɚ ɫ ɞɨɫɬɚɬɨɱ ɉɪɢ ɷɬɨɦ (14)
ɡɚɦɟɧɹɟɬɫɹ ɩɪɢɛɥɢɠɟɧɧɵɦ ɜɵɪɚɠɟɧɢɟɦ
N
N
|H
NN dd
ekbekb
k
k
F cos
2
1
sin
4
)(
22
d
e
k
N
¸
¹
¨
©
¸
¹
¨
©
N
22
tg
2
tg
2
cos
2
,
ɢ ɭɪɚɜɧɟɧɢɟ (13) ɩɪɢɧɢɦɚɟɬ ɜɢɞ
kbkkbkb
·§
N
·§
1
¸
¹
·
¨
©
§
N
¸
¹
·
¨
©
§
N
2
tg
2
tg
2
cos
2
kb
k
kkbkb
=
qa
e
d
cos2
N
. (16)
ɉɨɫɤɨɥɶɤɭ
ɩɪɢ0o
N d
e foNd , ɭɪɚɜɧɟɧɢɟ (16) ɩɪɟɞɟɥɟ ɛɟɫɤɨɧɟɱɧɨ
ɲɢɪɨɤɢɯ ɛɚɪɶɟɪɨɜ ()ɫɜɨɞɢɬɫɹ ɤ ɭɫɥɨɜɢɸ
ɜ
fod
0
2
tg
2
tg
¸
¹
·
¨
©
§
N
¸
¹
·
¨
©
§
kkb
N
kb
k
. (17)
Ɍɚɤɢɦ ɭɫɥɨɜɢɟɦ, ɫɨɝɥɚɫɧɨ ɮɨɪɦɭɥɚɦ (1) ɢ (2) ɡɚɞɚɱɢ 4.9, ɨɩɪɟɞɟɥɹɟɬɫɹ
ɞɢɫɤɪɟɬɧɵɣ ɫɩɟɤɬɪ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɭɪɨɜɧɟɣ
n
H ɜ ɨɞɢɧɨɱɧɨɣ ɩɪɹɦɨɭɝɨɥɶɧɨɣ
ɝɥɭɛɢɧ
, ɡɚɤɥɸɱɚɟɦ
ɩɨɬɟɧɰɢɚɥɶɧɨɣ ɹɦɟ ɨɣ
W ɢ ɲɢɪɢɧɨɣ b . ɋɱɢɬɚɹ ɬɟɩɟɪɶ
d
e
N
ɦɚɥɨɣ, ɧɨ
ɤɨɧɟɱɧɨɣ ɜɟɥɢɱɢɧɨɣ , ɱɬɨ ɪɟɲɟɧɢɹ )(
q
n
H ɭɪɚɜɧɟɧɢɹ ɨɛɪɚɡɭɸɬ
ɧɚ ɨɫɢ ɷɧɟɪɝɢɢ
ɡɨɧɵ – ɧɟ ɩɟɪɟɤɪɵɜɚɸɳɢɟɫɹ ɫ
ɜɛɥɢɡɢ ɷɧɟɪɝɟɬɢɱɟɫɤɢɯ ɭɪɨɜɧɟɣ
(16)
ɞɪɭɝ ɞɪɭɝɨɦ ɢɧɬɟɪɜɚɥɵ, ɥɟɠɚɳɢɟ
n
H ɨɞɢɧɨɱɧɨɣ ɹɦɵ.
Ɂɨɧɵ ɨɤɚɡɵɜɚɸɬɫɹ «ɭɡɤɢɦɢ» ɜ ɦɟɪɭ ɦɚɥɨɫɬɢ ɜɟɥɢɱɢɧɵ , ɢ ɩɨɷɬɨɦɭ
ɡɚɤɨɧ ɞɢɫɩɟɪɫɢɢ ɜ ɧɢɯ – ɡɚɜɢɫɢɦɨɫɬɶ ɷɧɟɪɝɢɢ ɨɬ q – ɥɟɝɤɨ ɭɫɬɚɧɨɜɢɬɶ, ɡɚɦɟɧɢɜ
ɮɭɧɤɰɢɸ )(
H
d
e
N
F
ɩɟɪɜɵɦɢ ɱɥɟɧɚɦɢ ɟɟ ɪɚɡɥɨɠɟ ɹ ɜ ɪɹɞ Ɍɟɣɥɨɪɚ ɩɨ ɫɬɟɩɟɧɹɦ
)(
n
HH :
()()()(
nnn
FFF
ɧɢ
)
H
H
H
c
H|H
ɍɱɢɬɵɜɚɹ ɪɚɜɟɧɫɬɜɨ 0)( H
n
F ɨɛɭɫɥɨɜɥɟɧɧɨɟ
.
, ɬɟɦ, ɱɬɨ ɭɪɨɜɧɢ
n
H , ɩɨ
ɫɭɳɟɫɬɜɭ, ɢ ɨɩɪɟɞɟɥɹɸɬɫɹ ɭɪɚɜɧɟɧɢɟɦ 0)(
H
F
, ɢɦɟɟɦ ɜ ɪɚɫɫɦɚɬɪɢɜɚɟɦɨɦ
ɩɪɢɛɥɢɠɟɧɢɢ:
=
qa
q
cos
1
)(
H H
. (18)
F
n
nn
)(
H
c
18
ȼ ɫɥɭɱɚɟ ɲɢɪɨɤɢɯ ɢ ɜɵɫɨɤɢɯ ɛɚɪɶɟɪɨɜ (1
N
d , 1
/
!!N k!! ) ɧɟɫɥɨɠɧɨɟ
ɜɵɱɢɫɥɟɧɢɟ ɞɚɟɬ:
D
bkF
n
n
n
H
|
H
c
2
)1(
)(
1
, (19)
1
ɝɞɟ ɜɟɥɢɱɢɧɚ
d
ekD
N
N|
2
2
/16 (
ɧɢɤɧɨɜɟɧɢɹ ɱɚɫɬɢɰɵ
ɱɟɪɟɡ ɜɵɫɨɤɢɣ ɩɨɬɟɧɰɢɚɥɶɧɵɣ ɛɚɪɶɟɪ;
ɡɧɚɱɟɧɢɹ
20)
ɩɪɟɞɫɬɚɜɥɹɟɬ ɫɨɛɨɣ ɜɟɪɨɹɬɧɨɫɬɶ
ɬɭɧɧɟɥɶɧɨɝɨ ɩɪɨ
k ɢ ɛɟɪɭɬɫɹ ɩɪɢN
n
H H .
(19), ȼɢɞɧɨ, ɱɬɨ ɤɨɷɮɮɢɰɢɟɧɬ
ɷɧɟɪɝɟɬɢɱɟɫɤɭɸ ɲɢɪɢɧɭ
ɨɣ ɡɨɧɵ, ɨɬɪɢɰɚɬɟɥɟɧ ɞɥɹ ɱɟɬɧɵɯ ɡɨɧ
ɩɨɪɨɠɞɟɧɧɵɯ ɭɪɨɜɧɹɦɢ , …, ɝɞɟ
ɶ ɨɫɧɨɜɧɨɝɨ ɫ
ɦ
ɗ
ɟɬ
2
; ɨɧ
ɢɟɦ ɷɧɟɪɝɢɢ ɱɚɫɬɢɰɵ ɫɭɳɟɫɬɜɟɧɧɨ
ɨɞɹɬɫɹ ɜ ɤɚɱɟɫɬɜɟɧɧɨɦ ɫɨɨɬɜɟɬɫɬɜɢɢ
ɟɣ ɹ ɜ .
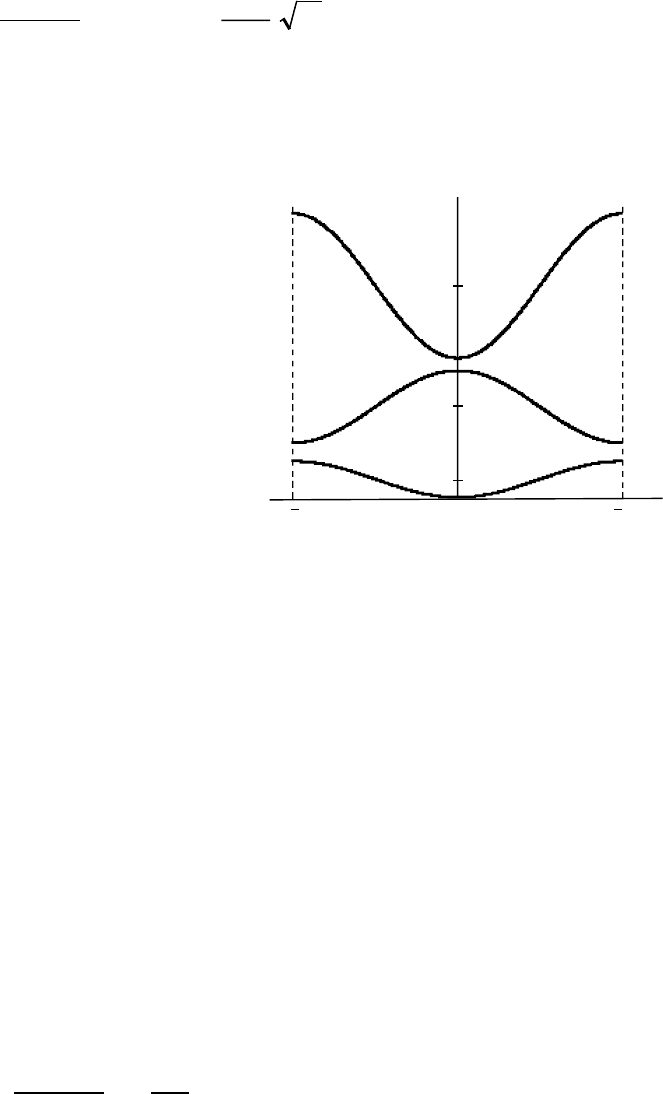
13) ɬɚɤɠɟ ɢɦɟɟɬ «ɡɨɧɧɵɣ» ɯɚɪɚɤɬɟɪ.
ɟ ɫɯɟɦɚɬɢɱɟɫɤɢ ɩɪɟɞɫɬɚɜɥɟɧɵ ɧɚ
ɨɩɪɟɞɟɥɹɸɳɢɣ
n -
(
0
H ,
2
H
0
H – ɭɪɨɜɟɧ ɨɫɬɨɹɧɢɹ ɜ
ɨɞɢɧɨɱɧɨɣ ɹ ɟ) ɢ ɩɨɥɨɠɢɬɟɥɟɧ ɞɥɹ
ɧɟɱɟɬɧɵɯ ɡɨɧ. ɧɟɪɝɟɬɢɱɟɫɤɚɹ ɲɢɪɢɧɚ
n -ɨɣ ɡɨɧɵ ɢɦɟ ɩɨɪɹɞɨɤ
1
D
n
H ɚ
ɪɚɫɬɟɬ ɫ ɪɨɫɬɨɦ ɧɨɦɟɪɚ ɡɨɧɵ, ɬɚɤ ɤɚɤ ɷɤɫɩɨɧ
ɩɨɞɛɚɪɶɟɪɧɨɝɨ ɩɪɨɯɨɠɞɟɧɢɹ
D ɫ ɩɨɜɵɲɟɧ
ɭɜɟɥɢɱɢɜɚɟɬɫɹ. ɉɨɥɭɱɟɧɧɵɟ ɪɟɡɭɥɶɬɚɬɵ ɧɚɯ
ɫ ɤɚɪɬɢɧɨɣ, ɪɚɫɫɦɚɬɪɢɜɚɜɲ ɫ ɡɚɞɚɱɟ 3.8
ȼ ɨɛɳɟɦ ɫɥɭɱɚɟ ɪɟɲɟɧɢɟ ɭɪɚɜɧɟɧɢɹ (
Ɉɬɦɟɱɟɧɧɵɟ ɜɵɲ ɱɟɪɬɵ ɬɚɤɨɝɨ ɪɟɲɟɧɢɹ
ɪɢɫ. 5.8.
5.6. ɚ) ɗɥɟɤɬɪɨɧ ɞɜɢɠɟɬɫɹ ɜ ɨɞɧɨɪɨɞɧɨɦ ɫɢɥɨɜɨɦ ɩɨɥɟ e
/
Sh/a Sh/a0
0
H
n
H (
H
2
H
1
q)
q
_
Ɋɢɫ. 5.8
ɟɧɰɢɚɥɶɧɨ ɦɚɥɵɣ ɤɨɷɮɮɢɰɢɟɧɬ
E
F
, ɤɨɬɨɪɨɦɭ
ɫɨɨɬɜɟɬɫɬɜɭɟɬ ɩɨɬɟɧɰɢɚɥɶɧɚɹ ɷ ɟɪɝɢɹɧ
x
F
x
U
)(. (1)
ɍɪɚɜɧɟɧɢɟ ɒɪɟɞɢɧɝɟɪɚ ɫ ɩɨɬɟɧɰɢɚɥɨɦ (1) ɢɦɟɟɬ ɜɢɞ
0)()(
2)(
22
2
\H
\
xxF
mxd
. (2)
xd
=
ɋɱɢɬɚɹ, ɱɬɨ ɩɨɫɬɨɹɧɧɚɹ
F
– ɩɨɥɨɠɢɬɟɥɶɧɚɹ ɜɟɥɢɱɢɧɚ, ɜɨɫɩɨɥɶɡɭɟɦɫɹ
ɦɚɫɲɬɚɛɨɦ ɞɥɢɧɵ
3/12
0
)2/( Fmx =
19
