Луизов А.В. Цвет и свет

Подождите немного. Документ загружается.

Если принять яркость единичного красного стимула за единицу (L

=1), то для

единичного белого цвета в системе RGB получим 1 + 4,5907 + 0,0601 = 5,6508; в системе

ХУZ яркость единичного белого цвета равна 1, отсюда а = 5,6508:1 = 5,6508.

Чтобы уравнять яркость белого в обеих системах, и вводят в системе ХУZ

дополнительный множитель и в результаты вычислений по формулам (8.19). Столь же

наглядна целесообразность множителя а и при сопоставлении координаты цвета у с кривой

видимости V(λ).

Пользуясь табл. 6.1, мы можем найти координаты спектрально–чистых цветов и,

подставляя их в формулу (8.19), определить для них y′(λ). Кривая у′(λ) как функция λ, для

спектральных цветов по форме совпадает с кривой V(λ), но проходит ниже ее. И для всех λ

V(λ)/у′(λ) = а. Значит, еслй умножить y′(λ) на а, обе кривые: совпадут; поскольку вся яркость

цвета в системе ХУZ передается координатой у′, совпаданйе кривой сложения с кривбй

относительной световой эффективности излучеиия V(λ) представляется совершенно

естественным.

Таблица 8.1. Ординаты кривых сложения (слева) и координаты цветности (справа)

монохроматических излучений в системе XYZ.

x(λ) y(λ) z(λ) λ,нм x(λ) y(λ) z(λ)

0,0014

0,0042

0,0143

0,0435

0,1344

0,2839

0,3483

0,3362

0,2908

0,1954

0,0956

0,0320

0,0049

0,0093

0,633

0,1655

0,2904

0,4334

0,5945

0,7621

0,9163

1,0263

1,0622

1,0026

0,8544

0,6424

0,4479

0,2835

0,1649

0,0874

0,0468

0,0227

0,0114

0,0058

0,0029

0,0000

0,0001

0,0004

0,0012

0,0040

0,0116

0,0230

0,0380

0,0600

0,0910

0,1390

0,2080

0,3230

0,5030

0,7100

0,8620

0,9540

0,9950

0,9520

0,8700

0,7570

0,6310

0,5030

0,3810

0,2650

0,1750

0,1070

0,0610

0,0320

0,0170

0,0082

0,0041

0,0021

0,0010

0,0065

0,0210

0,0679

0,2074

0,6456

1,3856

1,7471

1,7721

1,6692

1,2876

0,8130

0,4652

0,2720

0,1582

0,0782

0,0422

0,0203

0,0087

0,0039

0,0021

0,0017

0,0011

0,0008

0,0003

0,0002

0,0000

380

390

400

410

420

430

440

450

460

470

480

490

500

510

520

530

540

550

560

570

580

590

600

610

620

630

640

650

660

670

680

690

700

710

720

0,1714

0,1738

0,1733

0,1726

0,1714

0,1689

0,1644

0,1569

0,1440

0,1241

0,0913

0,0454

0,0082

0,0139

0,0743

0,1547

0,2296

0,3016

0,3713

0,4441

0,5125

0,5725

0,6270

0,6658

0,6915

0,7079

0,7190

0,7260

0,7300

0,7320

0,7334

0,7344

0,7347

0,0050

0,0048

0,0051

0,0069

0,0109

0,0177

0,0297

0,0578

0,1327

0,2950

0,5384

0,5702

0,8338

0,8059

0,7543

0,6923

0,6245

0,5547

0,4866

0,4242

0,3725

0,3340

0,3083

0,2920

0,2810

0,2740

0,2700

0,2680

0,2666

0,2656

0,2653

0,8209

0,8213

0,8219

0,8226

0,8235

0,8242

0,8247

0,8257

0,8263

0,8181

0,7760

0,6596

0,4534

0,2359

0,0919

0,0394

0,0161

0,0061

0,0024

0,0012

0,0009

0,0006

0,0005

0,0002

0,0001

0,0014

0,0007

0,0003

0,0002

0,0001

0,0005

0,0002

0,0001

0,0000

730

740

750

760

770

780

0,7347

0,2653

По аналогии с обозначениями в системе RGB координаты кривых сложения в системе

ХУZ будем обо значать

(λ),

(λ) и z (λ). Они получены как результат пересчета данных

табл. 6.1 по формуле (8.19), причем непосредственно вычисленные х(λ), у(λ) и z(λ)

умножены на а:

(λ) = ax(λ);

(λ) = ay(λ); z (λ) = az(λ)

В табл. 8.1 приведены вычисленные таким образом ординаты кривых сложения

системы ХУZ. По более точным расчетам а = 5,6504.

8.7. Согласованные формулы пересчета.

Чтобы не вычислять х′, у′ и z′ по формулам (8.19) и не умножать потом на а, умножим

заранее на 5,6504 все коэффициенты формулы. Однако новую формулу нужно согласовать с

уже ранее выведенными.

Рассмотрим простейший случай. Пусть у нас r′ = 1, g′ = 0, b′ = 0. Тогда

х' = а • 0,49000 • 1 = 2,7687;

у′ = a • 0,17697 • 1 = 1,0000;z′ = 0.

Теперь подставим х′, у′ и z′ в первую формулу (8.18), чтобы снова перейти в систему

RGB. Получим r′ = 2,36 461 • 2,7687 – 0,89 654 • 1 = 5,6504, т. е. уже не единицу, а величину,

в а раз большую. Конечно, этого можно было ожидать. Чтобы согласовать новые формулы

для х′, у′ и z′ с формулами обратного перехода, в формулах (8.18) все коэффициенты нужно

разделить на а. Окончательно находим

г′ = 0,4185x′ – 0,1587у′ – 0,0828z′;

g′ = –0,0912x′ + 0,2524у′ + 0,0157z′; (8.20)

b′ = 0,0009х′ – 0,0026у′ + 0,17862z′.

Для обратного пересчета r′, g′, b′ в координаты x′, y′, z′ приводим результат умножения

коэффициеитов формул {8.19) на а:

x′ = 2,7687r′ + 1,7516g′ + 1,1301b′;

у′ = 1,0000r′ + 4,5904g′ + 0,0601b′; (8.21)

z′ = 0.0000r′ + 0,0565g′ + 5,59396b′.

Для пересчета единичных цветов системы RGB в систему ХУZ остаются в силе

формулы .(8.14).

8.8. Ординаты кривых сложения системы XYZ.

Поскольку цвета ХУZ нереальны, нельзя построить колориметр, в котором они были

бы осуществлены как основные стимулы, Однако составить таблицу ординат кривых

сложения

(λ),

(λ) и z (λ) для системы ХУZ можно, вообще не прибегал к каким-либо

новым измерениям. Достаточно воспользоваться таблицей ординат кривых сложения для

системы RGB и по формулам (8.21) подставлять в них вместо r′, g′ и b′ значения

(λ),

(λ) и

b (λ) для спектрально-чистых цветов. Тогда вместо х′, у′ и z′ будут получаться ординаты

кривых сложения

(λ),

(λ) и z (λ), см. табл. 8.1.

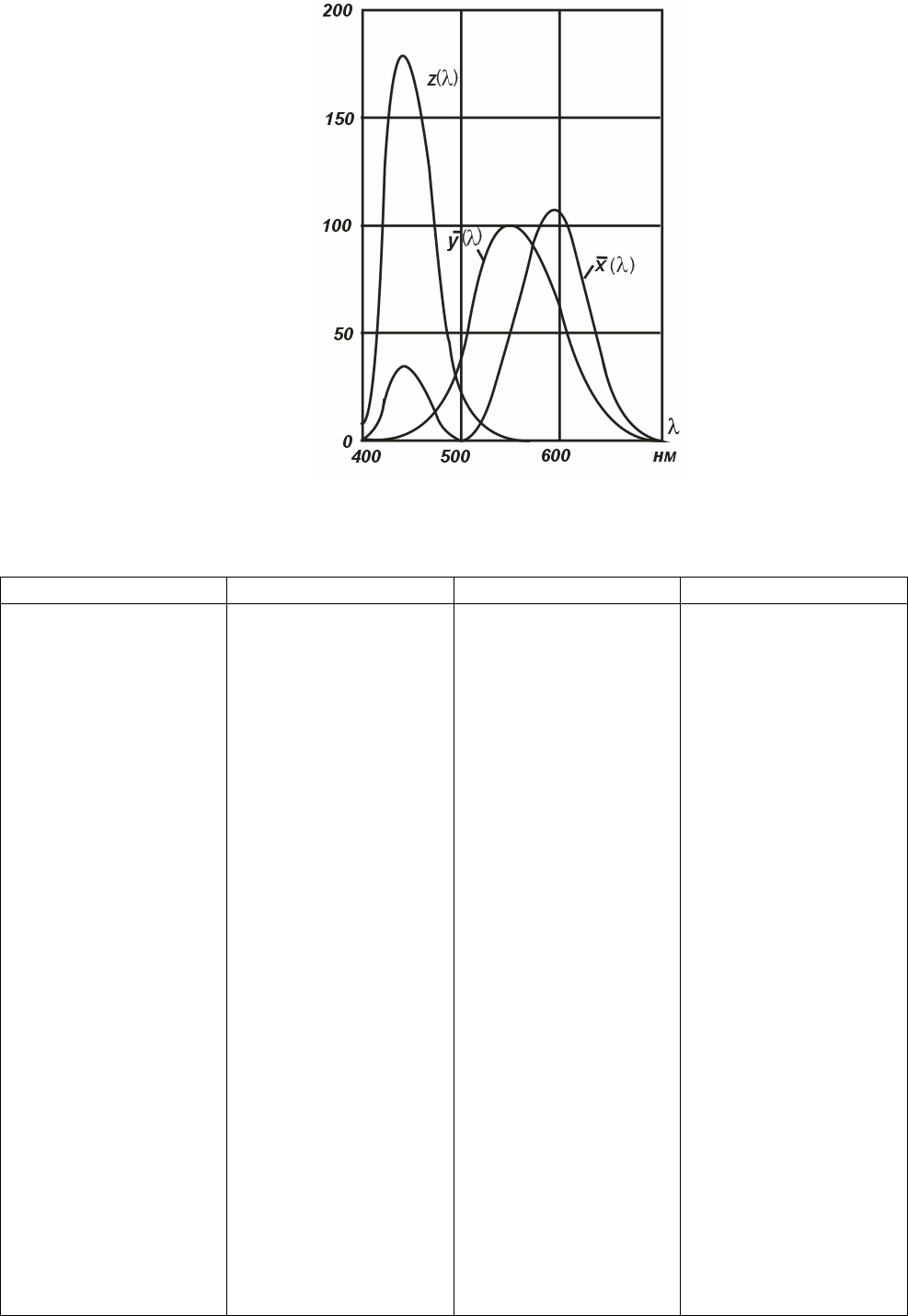
Рис. 8.2. Кривые сложения в системе XYZ.

Таблица 8.2. Ординаты кривых сложения для дополнительного стандартного

колориметрического наблюдателя МКО 1964 г.

λ,нм x

(λ) y

(λ) z

(λ)

380

390

400

410

420

430

440

450

460

470

480

490

500

510

520

530

540

550

560

570

580

590

600

610

620

630

640

650

0,000 2

0,002 4

0,019 1

0,084 7

0,204 5

0,314 7

0,383 7

0,370 7

0,302 3

0,195 6

0,080 5

0,016 2

0,003 8

0,037 5

0,117 7

0,236 5

0,376 8

0,529 8

0,705 2

0,878 7

1,014 2

1,118 5

1,124 0

1,030 5

0,856 3

0,647 5

0,431 6

0,268 3

0,000 0

0,000 3

0,002 0

0,008 8

0,021 4

0,038 7

0,062 1

0,089 5

0,128 2

0,185 2

0,253 6

0,339 1

0,460 8

0,606 7

0,761 8

0,875 2

0,962 0

0,991 8

0,997 3

0,955 6

0,868 9

0,777 4

0,658 3

0,528 0

0,398 1

0,283 5

0,179 8

0,107 8

0,000 7

0,010 5

0,086 0

0,389 4

0,972 5

1,553 5

1,967 3

1,994 8

1,745 4

1,317 6

0,722 1

0,415 3

0,218 5

0,112 0

0,060 7

0,030 5

0,013 7

0,004 0

0,000 0

660

670

680

690

700

710

720

730

740

750

760

770

780

0,152 6

0,081 3

0,040 9

0,019 9

0,009 6

0,004 6

0,002 2

0,001 0

0,000 5

0,000 3

0,000 1

0,000 0

0,060 3

0,031 8

0,015 9

0,007 7

0,003 7

0,001 8

0,000 8

0,000 4

0,000 2

0,000 1

0,000 0

Координаты цвета сложного излучения с распределением мощности по спектру Р

системе ХУZ вычисляются по формулам

∫

′

λλλλλλ

λλλ

dzPzdyPyxdxPx )( ;)( ;)( . (8.22)

Собранные в табл. 8.1 (слева) и изображенные в виде кривых на рис. 8.2 ординаты

кривых сложения рекомендованы Международной комиссией по освещению в 1931 г.

Испытуемые как у Райта, так и Гилда, на основе исследований которых были приняты

данные для стандартного наблюдателя 1931 г., проводили наблюдения центральным зрением

при поле зрения 2°. В такой области сетчатки работают только колбочки, с помощью

которых и осуществляется цветовое зрение. Палочки сами цвета не воспринимают, но,

работая совместно с колбочками, могут изменять цветовые восприятия. Поэтому были

проведены измерения для поля зрения, расширенного до 10°. Результаты таких измерений

были рекомендованы МКР в 1964 г. Ординаты кривых сложения для дополнительного

стандартного «колориметрического наблюдателя» собраны в табл. 8.2. Величины,

полученные с помощью этой таблицы, снабжаются индексом 10. Если не делается

специальных оговорок, все величины системы ХУZ следует рассчитывать для наблюдателя

МКО 1931 г., т. е. по табл. 8.1.

8.9. Цветность в системе XYZ.

Так же как в системе RGB, плоскость единичных цветов, т. е. плоскость цветности,

определяется уравнением

х' + у' + г' = 1, (8.23)

а координаты цветности х, у, z вычисляются по формулам

zyxm

′

= ; ; ;

. (8.24)

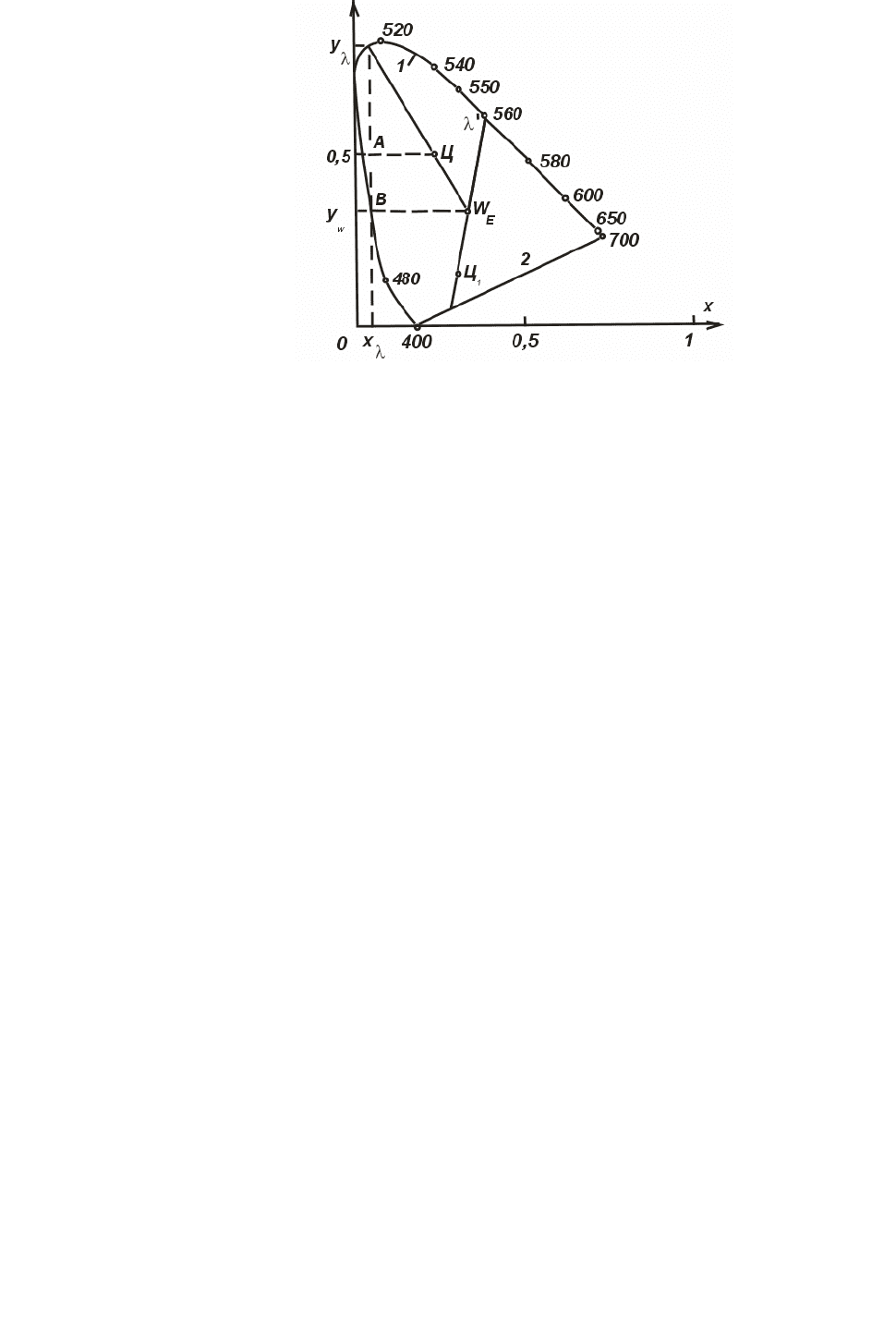
Рис. 8.3. Цветность на плоскости xy.

На рис. 8.3 изображена проекция плоскости цветности на плоскость ху. Кривой

спектрально–чистых цветов 1 и прямой пурпурных 2 ограничена область реальных цветов.

Видно, что координаты всех цветностей этой области (а следовательно, и соответствующих

им цветов) положительны. Точка W

белого равноэнергетического цвета имеет координаты

х = у = 1/3 (следовательно, и z = 1/3).

Чтобы найти цвет Ц(λ′), дополнительный к цвету Ц(λ), достаточно провести прямую

через точки λ и W

и продолжить ее до кривой спектралыю-чистых цветов 1.

Чтобы построить точку цвета Ц с координатами х, у и z, достаточно по формулам (8.24)

найти цветности его х и у. Смешением двух цветов с цветностями х

, у

и x

, у

можно

получить любые цветности х, у, которые лежат на отрезке прямой, соединяющей точки

(х

,у

) и (х

, у

). Линия, проведенная от точки λ = 700 нм до точки примерно λ = 540 нм,

очень близка к прямой (рис. 8.3), и поэтому, смешивая в разных пропорциях цвета,

соответствующие этим крайним точкам, можно получить все промежуточные цвета,

практически неотличимые от спектральночистых. После λ = 540 нм в направлении

уменьшення длины волн линия спектральных цветов все более искривляется, и,

следовательно, здесь смешение цветов всегда понижает чистоту цвета тем больше, чем

больше расстояние между точками, изображающима цветности смешйваемых цветов.

Из графика на рис. 8.3 видно, что цветности излучений при длине волны от λ = 660 нм

до λ = 770 нм изображены одной точкой, и глаз действиельно не различает цветиостей в этом

интервале. Заметим, что кривая спектральных цветов всюду выпуклая, что и обуславливает

понижение чистоты при смешении цветов (чистота, как правило, понижается

;

и только на

прямолййёйнбм участке остается практически равной единице). Если бы на кривой где–

нибудь была вогнутость, смешение могло бы дать повышение чистотьг {р>1), чёго никогда

не случается: ρ>1 – условие нереальности цвета. ,

8.10. Цветность и чувствительность приемников глаза.

В § 5.4 мы говорили об определении чувствительности трех цветовых приемников

глаза с помощью колориметрическйх измерений, проводимых дихроматами, т. е.

наблюдателями, у которых одйн из приемников не работает. Цветности, неразличимые про-

танопом, на графике ху ложатся на прямую линию, Если взять какую-нибудь другую

цветность и найти цветности, неотличимые от нее протанопом, мы получим другую прямую.

Таким образом, точки, соответ-ствующие неразличимым протанопом цветностям, образуют

ряд прямых. Продолжение их за пределы об-ластей реальных цветностей показывает, что

они сходятся в одной точке с координатами х

= 0,748; у

= 0,252 (следовательно, z

= 0) .

Индекс р показывает, что найденная точка получена для протанопа. Опыты с дейтеранопами

и тританопами дали аналогичные результаты, но прямые для них сходятся в других точках,

коордннаты которых, снабженные индексами d, для дейтеранопа и t для тританопа,

приводятся ниже:

Ось R

= 0,748; у

= 0,252; z

= 0;

Ось G

= 1,65; y

= –0,65; z

= 0;

Ось В

= 0,172; y

= –0,002; z

= 0,830

У протанопа не работает тот из приемников, который чувствителен к длинноволновой

части спектра и условно называётся красным. Поэтому координа x

и y

можно считать

координатами точки, в которой ось красного приемника пересекает плоскость цветностей

системы ХУZ. Это и отмечено на сводке координат указанием «Ось R

». Те же рассуждения

можно повторить относительно второй и третьей строк сводки. Таким образом, оказывается

найденным положение осей физиологической системы, т. е. системы трех приемников глаза.

Остальное – дело расчета, который проведен путем сопоставления системы RоG

системой ХYZ. В результате были получены формулы для единичных векторов системы

= 1,79Х + 0.603Y + 0,00Z;

= –1,00X + 0,395Y + 0,00Z; (8.25)

= 0,211X + 0,002Y + 1,00Z

и формулы для пересчета координат х', у' и z' в координаты физиологической системы r'

, g'

= 0,301x' + 0,765у′ – 0,066z';

g′

= –0,460x′ + 1,366у′ + 0,094z'; (8.26)

= 0,000x' + 0,000y′ + 1,000z'.

Пересчитав ординаты кривых сложения (см. табл. 8.1) системы ХУZ по формулам

(8.26), получили таблицу ординат кривых сложения системы R

Во, уже приведенную в

пятой главе (см. табл. 5.1).

Все рассказанное здесь об определении спектральной чувствительности приемников

глаза и о получении их количественных характеристик почерпнуто из работ Д. Н. Нюберга и

Е. Н. Юстовой (43).

8.11. Нормирование координат в системе XYZ.

Далеко не всегда нужно знать абсолютные значения координат х′, у′ и z′. Мы уже

видели, что часто вместо них даются координаты цветности, иначе говоря, производится

нормирование координат к единице (см. рис. 8.3). Но такое нормирование сопряжено с

существенными издержками: цвет – величина трехмерная, и две независимые координаты

полностью характеризовать его не могут. Зная цветность, мы ничего не можем сказать о

яркости цвета, если модуль m = х′ + у′ + z′ остается нам неизвестным. Во многих случаях,

однако, абсолютное значение яркости не представляет интереса. В § 4.2 уже было сказано,

что при изменении цвета несамосветящейся поверхности абсолютное значение яркости Ь

обычно не играет роли и может быть заменено коэффициентом диффузного отражения р.

Соответствующим нормированием и в системе ХУZ вместо абсолютной яркости

вводится некоторая относительная величина. Поскольку в системе ХУZ вся яркость

определяется координатой у′, нормирование проводят так, чтобы для поверхности, у которой

коэффициент диффузного отражения р = 1, значение у′

оказывалось бы равным 100 (по

существу, 100%) В формулы (8.22) вводят спектральный коэффициент отражения р(λ) и

нормирующий множитель 6 и получают

∫

′

λλλρλλλρλλλρ

λλλ

dzPkzdyPkydxPkx )()( ;)()( ;)()(

. (8.27)

Нормирующий множитель находят как отношение числа 100 к тому значению у′,

которое получается при условии р(λ) = 1 для всех длин волн видимой части спектра:

λλ

dyP

)(

100

∫

= . (8.28)

Аналогичным образом можно определять и координаты цвета излучения, прошедшего

через среду с селективным пропусканием, которое характеризуется спектральным

коэффициентом пропускания τ(λ). Вычисление координат цвета проводится тоже по

формулам (8.27) и (8.28), только вместо р(λ) ставится τ(λ). Пусть световой поток со

спектральной плотностью мощности Р

прошел сквозь фильтр со спектральным

пропусканием τ(λ). Напишем выражение для у′ прошедшего потока, заменив в формуле

(8.27) р(λ) на τ(λ) и подставив вместо k его выражение по формуле (8.28):

∫

′

λλ

λλλτ

dyP

)(

)()(100

. (8.29)

Ввиду того что у′ пропорционально яркости или световому потоку, отношение

интегралов в формуле (8.29) выражает интегральный коэффициент пропускания фильтра τ

для света со спектральной плотностью мощности Р

. Множитель 100 только переводит этот

коэффициент в проценты. Аналогично, если подставить в формулу (8.29) спектральный

коэффициент отражения р(λ), получим интегральный коэффициент отражения р. Итак, при

нормировании у′ = τ. (в процентах) либо у′ = р (в процентах).

Нормирование по формулам (8.27) и (8.28) делает безразличным, в каких единицах

выражена спектральная мощность излучения: в абсолютных или относительных, так как

любое изменение масштаба измерения Р

скажется одинаково на обоих интегралах в

формулах (8.27) и (8.28).

Для самосветящихся объектов нормированное значение у′ всегда будет получаться

равным 100. Вместе с тем именно для них, часто используемых как источники света, бывает

нужно знать абсолютную яркость L. Ее приходится находить отдельно, по формуле (23):

λλ

dyLKL

)(

∫

= . (8.30)

где Le

– спектральная плотность энергетической яркости, размерность которой Втм

срм

-1

;

= 683лм. Четвертый множитель в размерности L

eλ

соответствует единицам, в которых

измеряется длина волны, так что можно вместо обратных метров поставить, скажем,

обратные нанометры (нм

-1

8.12. О яркости единиц цвета.

Основы колориметрии особенно интенсивно разрабатывались в тридцатых и сороковых

годах. в Советском Союзе появились основополагающие труды М. М. Гуревича (13, 14), Т.

Н. Федорова (55), Е. С. Ратнера (48), С. О. Майзеля (36), Л. И. Демкиной (22) и др. Майзель и

Ратнер (36) совершенно определенно за единицы основных цветов принимают следующие

величины:

R λ = 700 нм; 1,0000 св = 243,9 Вт;

G λ, = 546,1 нм; 4,2907 св = 4,663 Вт

В λ = 435,8 нм; 0,0601 св = 3,384 Вт

Однако глаз не воспринимает светового потока непосредственно. Если разные световые

потоки будут поочередно направлкться на одну и ту же белую поверхность, ее яркость L,

каждый раз будет пропорциональна потоку Ф согласно формулам (3.6), (3.8). Поэтому с

точностью до некоторого постоянного множителя р/(πσ) световые потоки можно заменить

яркостями и положить, что для единицы R коэффициент яркости L

= 1; для единицы G

коэффициент яркости L

= 4,5907; для единицы В коэффициент яркости L

= 0,0601.

В. В. Мешков (40) тоже принимает абсолютные значения яркостных коэффициентов,

но иные, считая, что в системе ХУZ L

= 683 кд*м

-2

. Дело, однако, не в том, какие

конкретные значения придать яркостным коэффициентам, а в том, чтобы эти значения

сделать общепринятыми. Для этого нужен какой-то нормирующий документ, решение МКО

или национальный стандарт. Однако его до сих пор нет. Более того, попытки придать

яркостям единиц основных стимулов абсолютные значения встретили упорное со-

противление некоторых авторитетных колориметристов, в особенности Н. Д. Нюберга.

Противники введения определенных яркостей для единиц основных цветов утверждали, что

количественными величинами (поток, освещенность, яркость и т. д.) оперирует фотометрия,

а колориметрия изучает только качествен-яые характеристики цвета. Количественные, в

частности энергетические или световые, величины, в особенности яркость, колориметрии не

нужны. Но сам цветофизическая величина и без количественных характеристик определен

быть не может. Цвет трехмерен, и яркость прямо или косвенно входит в его компоненты. В

частности, от яркости зависит модуль цвета. Иcключая яркость, мы переходим от цвета к

цветности. Двухмерная цветность уже не характеризует полностью цвета. Наконец, в

системе λ, р, L яркость прямо выступает как одно из измерений цвета. И все же яркостным

коэффициентам L

, L

или L

не приписано определенных значений. По крайней мере, не

приписано официально ни в постановлениях МКО, ни в отечественных стандартах.

При переходе к системе ХУZ, в которой вся яркость характеризуется координатой у′,

можно было бы считать, что коэффициент яркости L

= 5,6504, а L

= L

= 0. Но как мы уже

писали в § 8.4, официально это не установлено, хотя множитель 5,6504 рекомендуется ГОСТ

13088–67 при переходе из системы RGB в систему ХУZ.

Существует некоторая неясность с ординатамн кривых сложения r(λ), g(λ), b(λ) и х(λ),

у(λ), z(λ), В стандарте они определены как координаты монохроматических излучений

единичной мощности. Следовательно, их размерность Вт

-1

, Действительно, если в формулу

(8.22), скажем для

λλ

dxPx )(

∫

′

мы подставим Pλ в ваттах на метр (или на нанометр – в зависимости от единиц, в которых

измерена длина волны λ), а

(λ) – в обратных ваттах, то получим для х′ нулевую

размерность, что совершенно естественно: координаты цвета безразмерны. Но в

Международном светотехническом словаре (39) на стр.65 сказано: «Координаты цвета могут

быть получены умножением ординат кривой относительного, спектрального распределения

излучения на ординать кривых сложения и интегрированием этих произведений по всей

спектральной области видимого излучения», т. е. вместо Р

в формуле (8.22) предполагается

ставить безразмерную величину φ(λ). Но тогда и x(λ) приходится считать величиной

безразмерной, иначе мы получим х′ в обратных ваттах (так жё как у′ и z′), что очевидно

нелепо. Сейчас .официально признано несовершенство ряда руководящих материалов в

области колориметрии и ведется работа по их упорядочению. Попробуем, однако, не

дожидаясь новых официальных предписаний, решитй вопрос о яркости цвета вполне

корректно.

Не нарушая никаких узаконений или обычаев, мы можем пропорциональность

яркостей единид основных стимулов их яркостным коэффициентам записать таким

способом:

L(R) = KL

; L(G) = KL

; L(В) = KL

. (8.31)

Если поделить эти выражения друг на друга, K сократится и мы получим

L(R): L(G): L(В) = L

: L

= 1: 4,5907: 0,0601, (8.32)

т. е. по существу, общепринятую формулу (6.1). Вместе с тем, поскольку коэффициенту К

мы можем приписывать любое значение, ничего не мешает считать, что

= 1; L

= 4,5907; L

= 0,0601 . (8.33)

Аналогичные соображения в системе ХУZ дают

Lх = 0; L

= 1; L

= 0. (8.34)

Таким образом, яркость любого цвета L(Ц) в системе RGВ будет

L(Ц) = K(r′L

+ g′L

+ b′L

)

(8.35)

В системе

L(Ц) = Ky′L

= Ky′ (8.36)

Если абсолютные яркости в той или иной работе несущественны, коэффициенты К

можно не конкретизировать. Необходимо только, чтобы, скажем, при сложении цветов у

всех слагаемых коэффициент K был одинаков. Размерность коэффициента K, как этр

явствует из формул (8.31) – (8.36), должна быть кд*м

-2

. Если положить К численно равным

максимальной световой эффективности K

, это даст основание в формулах (8.35) или (8.36)

принимать К=683кд*м

-2

, т, е.

L(Ц) = 683 (r' + 4,5907g' + 0,0601b'); (8.37)

L(Ц) = 683y′ (8.38)

Значения яркостных коэффициентов для (8.37) взяты те, что указаны в (8.33).

Размерность численного коэффициента кд*м

-2

Именно таким способом определяют яркости цве-га В. В. Мешков (40), В. А. Зернов

(25), Б. А. Шашлов (59), А. В. Луизов (31). Конечно, яркость любого цвета остается той же

самой, подсчитаем ли мы ее по формуле .(8.37) или (8.38), что легко проверить,

воспользовавшись формулами перехода (8.20) или .(8.21) из одной системы в другую.

8.13. Цвет и цветность.

Хотя мы уже достаточно ясно сказали, чем цветность отличается от цвета, хотим еще

раз подчеркнуть различие между этими величинами.

Пусть перед нами лежат два куска ткани одинаковой цветности, освещенные одним и

тем же источником света, скажем лампой накаливания. Освещенность Е обоих кусков тоже

одинакова. В чем может проявиться различие между ними, если цвет их неодинаков? Только

в яркости, которая зависит от интегрального коэффициента отражения р. Один кусок может

бказаться темнее другого. Цвет может быть определен только тремя независимыми

величинами: r′, g′, b′; λ, р, р; г, g, р или х′, у′, z′, причем при нормировании, соответствующем

формулам (8.27) и [(8.28), у' играет роль коэффициента отражения.

Но, строго говоря, величина, определенная по этим формулам, – еще не совсем цвет.

Ведь если мы приблизим источник к ткани, ее яркость возрастет. Не будь нормирования, все

три координаты х′, у′ и z′ возросли бы в одинаковое число раз; при этом модуль цвета, а

следовательно, все координаты цвета тоже увеличились бы в одинаковое число раз.

Нормирование (8.28) препятствует такому увеличению, Но для несамосветящегося объекта

абсолютное знание модуля несущественно.

Существенным оно может быть для самосветящейся поверхности, для которой и

следует указывать абсолютные значения координат λ, р и L или г′, g′ и b′ либо вычислять

абсолютную яркость по формуле (8.30).

8.14. Определение доминирующей длины волны λ и чистоты цвета ρ.

Пусть нам дан некоторый цвет Ц, координаты цветности которого х, у. На графике

рис. 8.3 он изображается точкой Ц. Проведя через точку белого цвета W

и точку Ц прямую и

продолжив ее до пересечения с линией спектрально-чистых цветов 1, получим точку,

которая и укажет доминирующую длину волны λ цвета Ц.

Яркость цвета Ц характеризуется координатой у. Она составлена из яркости

спектрально-чистого цвета у

и яркости белого у

. Обозначив долю спектрально-чистого

цвета символом n, напишем

y = ny

+ (1 – n) у

Очевидно, что р = ny

/у. Чтрбы найти n, проведем через точки Ц и W

прямые,

параллельные оси абсцисс, до пересечения их с прямой, проведенной из точки λ

перпендикулярно оси абсцисс. Очевидно, что в цвете Ц будет тем больше спектрально-

чистого, чем дальше точка Ц от точки W

. Но расстояние между Ц и W

нужно относить ко

всему расстрянию от λ до W

. В силу подобия треугольников АλЦ и ВλЦ отношение

гипотенуз W

λ и Цλ можно заменить отношением катетов Вλ и Aλ и написать

−

;

следовательно,

−

= . (8.39)

В силу подобия уже упомянутых треугольников отношение вертикальных катетов

можно заменить отношением горизонтальных и получить

−

(8.40)

Формулы (8.39) и (8.40) равноценны, но в каждом конкретном случае более точный

результат даеи та, в которой разности, стоящие в числителе и знаменателе, больше.

Для цвета Ц

прямая, проведенная от W

к Ц (рис. 8.3), пересечет линию пурпурных

цветов 2. Продолжая прямую в другую сторону, получим λ′ – цвет, дополнительный к

пурпурному. Чистоту пурпурного цвета λ′ следует определять по тем же формулам (8.39) или

(8.40).

Для полного определения цвета в системе λ, р, L нужны сведения о значении

координаты цвета у′. Если она будет нормирована по формулам (8.27), (8,28), мы получим

вместо L коэффициент диффузного отражения р (в процентах).

8.15. Плоскость равной яркости.

В системе ХУZ плоскость равной яркости, т. е. плоскость, в которой изображаются

цвета, равные по яркости, описывается совсем простым уравнением

y′ = const. (8.41)

Придавая постоянной в (8.41) разные значения, мы получим ряд параллельных

плоскостей, идущих перпендикулярно оси у.

В системе RGВ поверхность равной яркости – тоже плоскость; это ясно уже из того,

что она может быть получена линей.ным преобразованием координат системы ХУZ в

систему RGВ. Уравнение плоскости рйвнбй яркости легко получить, взяв из формул (8.21)

уравнение для у′ и придав у′ любое постоянное значение:

1,00000r′ + 4,59038g′ + 0.06006b' = const.

Снова придавая константе разные значения, получим ряд параллельных плоскостей

равной яркости.

Глава 9. Получение хроматических цветов и их смешение

9.1. Краски.

Мы принимаем дневной свет за белый, ахроматический. Но большинство предметов:

листья деревьев, стены домов, мебель – видим цветными. Они отражают свет селективно:

излучение некоторых длии волн сильнее, других слабее. Так, поверхность, освещенная

ахроматическим светом, приобретает хроматический цвет. Перед нами стол, поверхность

которого покрыта окрашенным лаком. Лак сам по себе прозрачен (во всяком случае в

довольно тонком слое покрытия). С ним перемешено огромное количество мелких частиц

пигмента. Входящий в слой лака белый свет рассеивается частицами пигмента, и часть света

выходит из слоя. Но рассеяние света частицами пигмента – сложный процесс. На

поверхностй частицы часть света отражается (рассеивается), а часть входит в частицу и

проходит сквозь нее. А пигмент избирательно поглощает свет. Белый свет, вошедший в

частицу, выходит из нее окрашенным. Дальше он встречает другие частицы и, рассеянный

|ими, может выйти из слоя лака наружу. В результате из слоя выходит уже небелый свет.

Приближенно можно сказать, что выходящее из слоя излучение имеет цвет, дополнительный

к цвету излучения, преимущественно поглощаемого частицами пигмента.

Напомним, что каждый атом в невозбужденном состоянии обладает некоторой

энергией Е

. Тот же атом может находиться и в ряде состояний с другими энергиями (Е

,..., Е

, ..., Е

и т. д.). Чтобы перейти в состояние с большей энергией Е

, т. е. возбудиться,

атом должен поглотить порцию энергии ∆Е, причем ∆E = Е

– Е

или, если атом был уже

предварительно возбужден и обладал энергией Е

для перехода в состояние с энергией Е

нужна порция энергии ∆E=Е

—Е

. Невозбужденный атом может поглощать излучение