Луизов А.В. Цвет и свет

Подождите немного. Документ загружается.

Раутиан рекомендует считать, что если 1<N<3, цветоаномалии у испытуемого нет.

Такие значения N можно считать лежащими в пределах естественных вариаций

цветоощущения,

Если 3<N<10, это цветослабость (на I этапе исйытаний – протаномалия). Если N>10, это

уже сильная цвеослабость (субдихроматизм), а если N>40, это дихроматизм (на 1 этапе -

протанопия). Поворотом дисков П и Л вводят последовательно фильтры на этапах II, III, IV.

Этап II позволяет провести испытание на дейтеранопию, этап III – на тританопию. Этап

IV, в сущности, совпадает с испытанием по схеме Релея и может дать некоторые

дополнительные сведения о зрении испытуемого.

Аномалоскоп Раутиана (модель АН-59) около тридцати лет серийно выпускается в

Советском Союзе. Сейчас проводится разработка новой систумы с целью упрощения и

ускорения исследований цветового зрения.

Глава 6. Система RGB.

6.1. Выбор основных цветов.

Согласно трехкомпонентной теории зрения любое излучение из видимой части спектра,

воздействуя на глаз, возбуждает три светочувствительных вещества сетчатки, и в

зависимости от степени их возбуждения мы воспринимаем тот или иной цвет. Некоторые

излучения возбуждают только два или даже только одно вещество, но это не имеет

принципиального значения.

Пусть какое-то излучение, монохроматическое или состоящее из смеси излучений с

разными длинами волн, так возбуждает три приемника, что человек ощущает цвет Ц. Уже

Максвелл показал, что тот же цвет Ц можно получить, смешивая три излучения в

соответствующей пропорции – см. формулу (5.1). Эта формула позволяет однозначно

определить любой цвет Ц, если известны три другие цвета, выбранные как основные.

Напомним, что Максвелл пользовался тремя монохроматическими излучениями с

длинами волн 630, 528 и 457 нм. Другие ученые выбирали для измерения цвета иные три

излучения. Излучения, которые кладутся в основу системы цветовых измерений, называют

основными стимулами. Чтобы получить единую систему цветовых измерений, нужно прежде

всего установить, стандартизировать три основных стимула, разумно их выбрав.

Что значит выбрать разумно, мы выясним позже, а пока укажем только одно

безусловное требование: все три стимула должны быть линейно не зависимы друг от друга.

Независимость означает, что ни один из основных цветов не может быть получен смешением

двух других. Несоблюдение условия независимости показывает, что, по существу, выбрано

не три, а только два основных цвета. Такая система цветовых измерений могла бы устроить

лишь дихромата.

В области светотехники и близких к ней дисциплин значение величин, методы

расчетов, рекомендуемые для всех стран, устанавливает Международная комиссия по

освещению – МКО (СIЕ – Commission International de l’Eclairage). В 1931г. на VIII сессии

МКО было принято решение выбрать в качестве основных цветов – основных стимулов –

три монохроматических излучения с длинами волн λ

= 700 нм, λ

= 546,1 нм и λ

= 435,8 нм

[39]. Выбранные стимулы удобны тем, что два из них (В и R) близки к краям видимого

спектра, а третий (G) близок к его середине. Кроме того, излучения λ

и λ

с большой

интенсивностью испускаются парами ртути. Обозначения R, G и В даны по начальным

буквам слов «красный», «зелеиый», «синий»: по-английски геd, green, blue, по-немецки rot,

grun, blau.

6.2. Базисный стимул.

Кроме трех основных стимулов R, G и В для установления единиц цветовых координат

необходим еще четвертый, называемый базисным. Базисный стимул – некоторый цвет,

обычно ахроматический, который должен получиться при сложении основных стимулов в

равных количествах. Для системы RGB в качестве базисного стимула принят белый

равноэнергетический W

Пусть для получения белого равноэнергетического цвета пришлось сложить три

основных стимула с яркостями КL

, КL

и КL

. Оказывается, что эти яркости отнюдь не

равны друг другу. Яркость зеленого больше всех, красного меньше, синего еще меньше.

Отношение яркостей после сокращения коэффициента К таково:

: L

= 1: 4,5907: 0,0601. (6.1)

Стоящие слева величины называют яркостными коэффициентами. Для того чтобы

сложение равного числа единиц основных стимулов давало белый равноэнергетический

цвет, яркости единиц должны быть пропорциональны их яркостным коэффициентам:

L(R) = КL

; L(G) = КL

; L(B) = КL

. (6.2)

Так как в выборе коэффициента пропорциональности K мы ничем не связаны, можем

вместо L

, L

и L

подставить стоящие справа в формуле (6.1) числа и получить

L(R) = К; L(G) = 4,5907К; L(B) = 0,0601К. (6.3)

Пусть на одном поле колориметра создан подлежащий измерению цвет Ц. Чтобы

сделать поля колориметра неотличимыми по цвету, на другом поле потребовалось смешать

основные стимулы с яркостями L

, L

и L

. Тогда координаты цвета Ц r', g′ и b' можно найти

по формулам

)B(

' ;

)G(

'g ;

)R(

=== . (6.4)

Теперь можем написать

Ц = r’R + g’G + b’B. (6.5)

Здесь ясно видна трехмерность цвета, Ц – вектор в трехмерном пространстве; R, G и В

– его орты; r', g' и b' – координаты по трем осям.

Белому равноэнергетическому стимулу соответствует условие

r' = g' = b'. (6.6)

6.3. Схема колориметра.

Для того чтобы сделать более понятным дальнейшее изложение, следует познакомить

читателя с тем, как сравнивают цвета, устанавливают равенство одного цвета с другим, в

частности неизвестного цвета с цветом, координаты которого известны, что и позволяет

измерить неизвестный цвет. Прибор для измерения цвета называется колориметром. Одна из

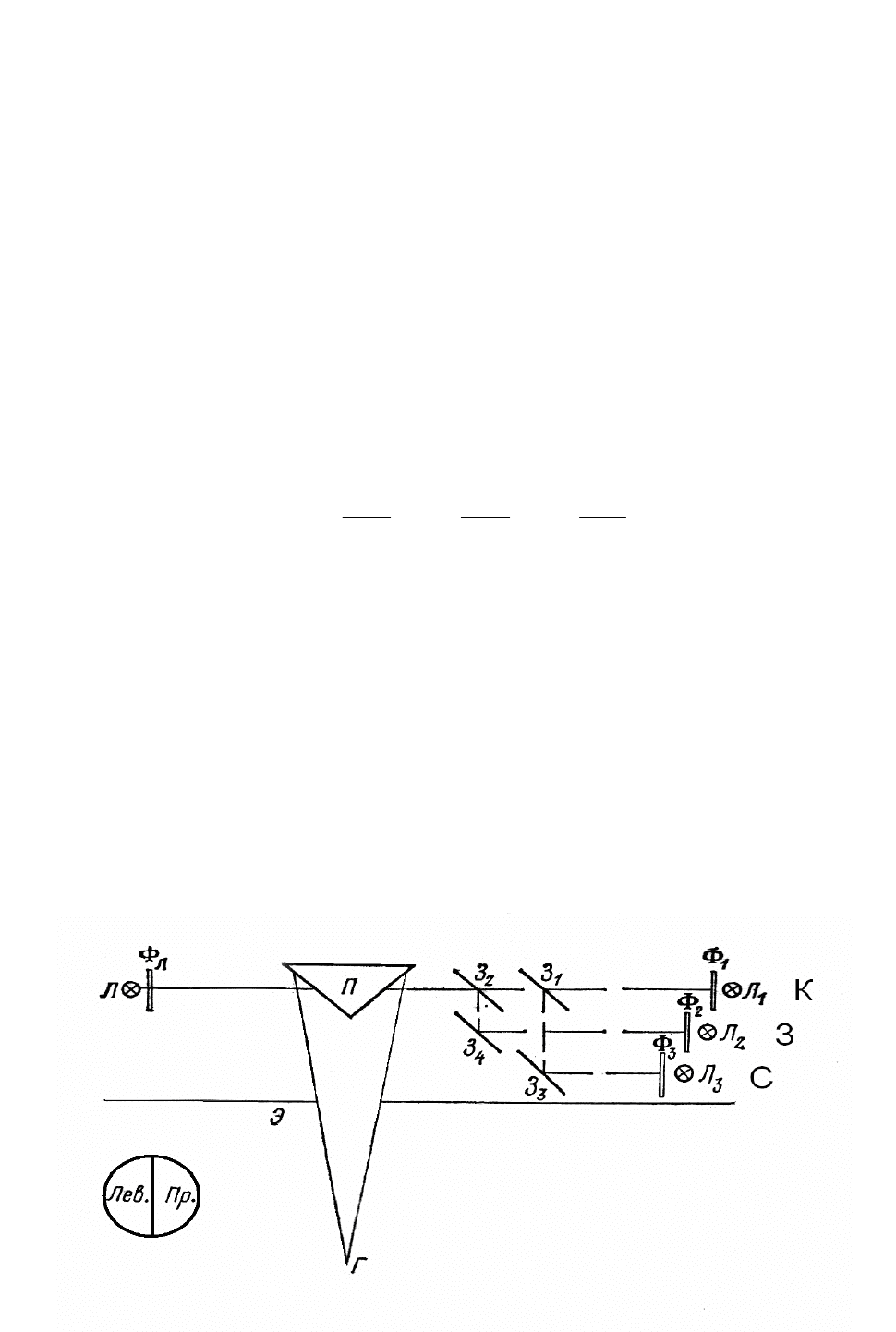
возможных схем колориметра изображена на рис. 6.1.

Рис. 6.1. Схема простейшего колориметра.

Два смежных поля, на которых создаются сравниваемые цвета, могут быть такими же,

как у фотометра, о котором говорилось в § 3.3 (см. рис. 3.1). Но способ освещения сторон

белой призмы П (рис. 6.1) в колориметре сложнее, чем в фотометре. Левая сторона

освещается излучением, цвет которого следует измерить, например светом лампы Л,

проходящим сквозь цветное стекло Ф

. Правая грань призмы освещается тремя источниками

света. Измерения будут упрощены, если излучения от ламп Л

, Л

и Л

будут близки к

монохроматическим с длинами волн λ

= 700 нм, λ

= 435,8 нм и λ

= 435,8 нм, т. е совпадать

с излучениями λ

, λ

и λ

. Этого можно достигнуть, поставив перед лампами Л

, Л

и Л

узкополосные, например интерференционные (56), светофильтры Ф

и Ф

Зеркала З

и З

отражают падающий на них свет по возможности полностью, зеркала З

и З

частично отражают, частично пропускают свет. Если, например, зеркало З

пропускает

половину света, а зеркало З

– 66%, то от каждого из источников до призмы П будет

доходить примерно одна треть направляемого ими на призму света (без учета потерь при

отражении и пропускании). Человек, производящий измерение, помещает свой глаз в точку Г

и в круглое отверстие в экране Э видит часть призмы П, как этоизображено в нижней части

рисунка, слева. С помощью какого-либо механизма наблюдатель может перемещать

источники Л

, Л

и Л

, приближая к призме П или удаляя каждый из них. Положение ис-

точников, т. е. расстояние их от призмы, отмечается на трех шкалах, и каждому расстоянию

соответствует своя освещенность Е

, Е

или Е

, создаваемая источниками Л

, Л

или Л

соответственно.

Наблюдатель перемещает источники до тех пор, пока не уравняет цвет обоих полей Л и

П. Может, однако, случиться, что установить равенство по цвету ему не удается вследствие

разницы в яркостях полей Л и П. Тогда можно передвинуть источник Л, освещающий левое

поле призмы, изменить его освещенность E

, а следовательно, и яркость, не меняя спек-

трального состава измеряемого излучения.

Экран Э ограничивает поле зрения наблюдателя, позволяя ему видеть только часть

призмы П. Диаметр видимого в отверстие в экране кружка в угловой мере обычно не

превышает двух градусов. Экран Э освещается так, чтобы яркость его мало отличалась от

яркости призмы П.

Полученные освещенности Е

, Е

и Е

могут быть пересчитаны в три составляющие

цвета поля Л. О способах пересчета мы расскажем позже.

Реально существующие колориметры устроены иначе. О них более подробно будет

рассказано в главе 10. Сейчас важно отметить одно: в большинстве колориметров

предусмотрена возможность перебросить любое из трех излучений правой части на левую

стороцу призмы П, добавив его к изучаемому пзлучению. Скоро мы узнаем, для чего это

нужно.

6.4. Кривые сложения RGB.

В основу системы RGB было положено измерение с ее помощыо основных стимулов

монохроматических излучений видимой части спектра. Представим себе такое измерение с

помощыо только что описанного колориметра. Разобьем видимый спектр от λ = 380 нм до

λ = 770 нм на участки по 5 нм каждый, всего 78 участков. Вместо источника Л (см. рис. 6.1)

поставим монохроматор, который будет выделять последовательно участки спектра по 5 нм

и •освещатъ их излучением левую грань призмы П.

Таблица 6.1 Ординаты кривых сложения (слева) и координаты цветности (справа)

монохроматических излучений в системе RGB.

r(λ) g(λ) b(λ) λ,нм r(λ) g(λ) b(λ)

0,0000

0,0001

0,0003

0,0008

0,0021

0,0022

0,0026

–0,0121

–0,0261

–0,0393

–0,0494

–0,0581

–0,0717

–0,0890

–0,0926

–0,0710

–0,0315

0,0228

0,0906

0,1677

0,2453

0,0000

–0,0001

–0,0004

–0,0011

–0,0012

0,0015

0,0068

0,0148

0,0254

0,0391

0,0569

0,854

0,1286

0,1747

0,2032

0,2147

0,2118

0,1970

0,1709

0,1361

0,0012

0,0036

0,0121

0,0371\

0,1154

0,2477

0,3123

0,3167

0,2982

0,2299

0,1449

0,0826

0,0478

0,0270

0,0122

0,0055

0,0015

–0,0006

–0,0013

–0,0014

–0,0011

380

390

400

410

420

430

440

450

460

470

480

490

500

510

520

530

540

550

560

570

580

0,0272

0,0263

0,0247

0,0225

0,0181

0,0088

–0,0084

–0,0390

–0,0309

–0,1821

–0,3667

–0,7150

–1,1685

–1,3371

–0,9830

–0,5159

–0,1707

0,0974

0,3164

0,4973

0,6449

–0,0115

–0,0114

–0,0112

–0,0109

–0,0094

–0,0048

0,0048

0,0218

0,0517

0,1175

0,2906

0,6996

1,3905

1,9318

1,8534

1,4761

1,1628

0,9051

0,6881

0,5067

0,3579

0,9843

0,9851

0,6865

0,9884

0,9913

0,9960

1,0036

1,0172

1,0392

1,0646

1,0761

1,0154

0,4780

0,4053

0,1296

0,0398

0,0079

–0,0025

–0,0045

–0,0040

–0,0028

0,3093

0,3443

0,3397

0,2971

0,2268

0,1597

0,1017

0,0593

0,0315

0,0169

0,0082

0,0041

0,0021

0,0010

0,0005

0,0002

0,0001

0,0000

0,0975

0,0625

0,0356

0,0183

0,0083

0,0033

0,0012

0,0004

0,0001

0,0000

–0,0008

–0,0005

–0,0003

–0,0002

–0,0001

–0,0000

590

600

610

620

630

640

650

660

670

680

690

700

710

720

730

740

750

760

770

0,7617

0,8475

0,3059

0,9425

0,9649

0,9797

0,9888

0,9940

0,9966

0,9984

0,9996

1,0000

0,2402

0,1537

0,0949

0,0580

0,0354

0,0205

0,0113

0,0061

0,0035

0,0016

0,0004

0,0000

–0,0019

–0,0012

–0,0008

–0,0005

–0,0003

–0,0002

–0,0001

–0,0000

С помощью каких-либо приспособлений – регулировкой ширины щели, серых клиньев

и т. п. – добьемся того, чтобы при каждой установке монохроматора мощность излучения,

попадающего на правое поле сравнения, была одной и той же, например 1 Вт (для

упрощения). При каждой установке будем уравни-вать свет левой грани призмы с цветом

правой и за-писывать освещенности от каждого из источников Л

, Л

и Л

. В результате

получим таблицу (табл. 6.1), в которой против каждой длины волны λ слева будут стоять три

величины, называемые ординатами кривых сложения, а справа – три величины, называемые

цветовыми координатами спектрально-чистых стимулов единичной мощности. Каждая из

них показывает, сколько единиц соответствующего основного цвета (R, G или В) нужно

взять, чтобы получить цвет излучения с длиной волны λ и мощностью 1 Вт. У каждого

человека кривые сложения несколько отличаются друг от друга. Однако, если в качестве

испытуемых подбирать нормальных трихроматов, отличия получаются не слишком

большими. В. Райт провел измерения с десятью испытуемыми, Дж. Гилд – с семью (23).

Результаты обоих исследований оказались достаточно близкими, и решением МКО в 1931 г.

на их основе были приняты значения ординат кривых сложения системы RGB, которые

представлены в табл. 6.1 и в виде графика на рис. 6.2.

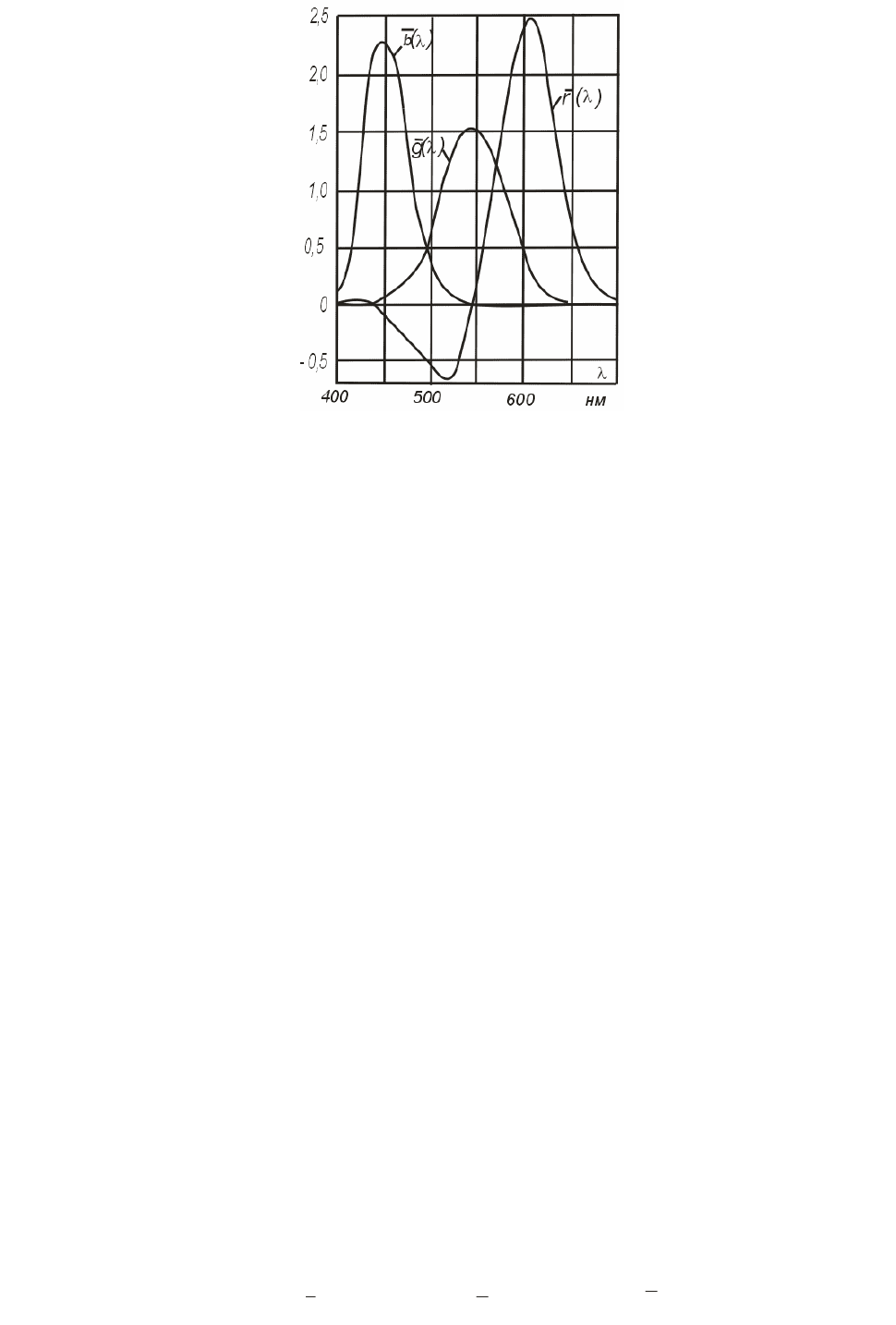
Рис. 6.2 Кривые сложения в системе RGB

6.5. Координаты цвета.

Измерить цвет Ц – значит определить три его составляющие, три координаты цвета r′,

g′ и b′. Координата r′ равна числу единиц основного цвета R, координата g′ – числу единиц

цвета G, координата b′ – числу единиц цвета В в цвете Ц. Цвет Ц может быть получен в

колориметре на левой грани призмы П (см. рис. 6.1) либо непосредственно освещением ее

лампой Л, либо сочетанием лампы Л с фильтром, либо помещением на левую грань призмы

цветного рассеивающего образца, освещаемого лампой Л. Шкалы колориметра, по которым

отсчитываются перемещения источников Л

, Л

и Л

в правой части колориметра, могут быть

градуированы так, чтобы давать сразу координаты цвета r′, g′ и b′ при условии, что цвет

правой грани призмы уравнен с цветом левой грани.

Нередко случается, что установить равенство обычным путем не удается. Дело в том,

что смесь двух или большего числа даже спектрально-чистых излучений дает обычно менее

чистый цвет, чем смешиваемые излучения. Поэтому часто приходится переключать одно из

основных излучений, например R, на левую часть призмы, подмешивать его к измеряемому

цвету, снижая его чистоту, как говорят колориметристы, разбавляя измеряемый цвет. В

цветовом равенстве такое перенесение основного излучения на сторону измеряемого

учитывается тем, что соответствующей координате придается отрицательное значение.

Когда три координаты цвета Ц определены, для него можно написать равенство, подобное

равенству (5.1):

Ц = r’R + g’G + b’B,

где R, G и В – единичные векторы (орты) соответствующих основных цветов.

Каждой единице цвета соответствует своя яркость, определяемая ее яркостным

коэффициентом. Поэтому для получения полной яркости цвета Ц, нужно сложить яркости

составляющих двета:

= L

r’ + L

g’ + L

b’. (6.7)

Однако здесь яркость Lц мы получаем в относительных единицах, т. е. находим

величину, которой пропорциональна яркость цвета. Как явствует из анализа формул (6.2),

(6.3) и (6.4), яркостные коэффициенты – величины безразмерные; отсюда и Lц безразмерна.

Цвет можно не только непосредственно измерить, но и вычислить,. если известна

спектральная плотность мощности излучения P

в видимой области спектра. Вычисление

производится с помощью формул, аналогичных формулам (5.2) :

λλλλλλ

λλλ

dbPbdgPgdrPr )(' ;)(' ;)('

∫

=== . (6.8)

Интегралы берутся в пределах видимой области спектра. Спектральную плотность

мощности излучения P

можно измерить с помощью монохроматора, который будет описан в

главе 9. Формулы (6.8) определяют связь между спектральным составом и цветом излучения.

Данному спектральному составу излучения соответствует один и только один его цвет.

Рднако отсюда отнюдь не следует обратное заключение, что каждому цвету соответствует

один определенный состав излучения. Такое утверждение ошибочно.

6.6. Метамеризм.

Приведем такой пример. Пусть имеются два металла, из которых нужно сделать сплав.

Соотношением массы двух составляющих сплава определится его плотность. И данной

плотности будет соотвествовать только одно соотношение количеств двух металлов.

Вспомните задачу, которую блёстяще решил Архимед. Но если речь идет о сплаве трех

металлов, дело меняется. Данному сочетанию компонентов отвечает одна плотность, но та

же плотность может быть получена и при других пропорциях. Если мы сплавим три металла,

имеющие плотность m

, m

, mz причем доля каждого будет х, у и z, плотность сплава будет

zmmymmxmm

mmm

yxzxzy

zyx

. (6.9)

Но, зная ш, мы не сможем найти x, y и z, так как уравнений будет только два (второе

х + у + z = 1), а неизвестных три. Наличие только двух компонентов равносильно условию

z = 0, после чего данное значение m можно получить лишь при одной паре значений х и у.

Известно, что белый свет можно получить, смешивая все цвета радуги (этот опыт

проводил еще Ньютон) или всего два монохроматических излучения, надлежащим образом

выбранных. Два излучения, которые, будучи смешаны в надлежащей пропорции, дают белый

цвет, называются взаимно дополнительными. Таких взаимно дополнительных излучений

бесконечное множество. Какой-нибудь иной цвет может получаться при смешении двух,

трех или большего числа излучений. То же относится и к излучениям сплошного спектра,

распределение Р

в которых может быть различным, а цвет одним и тем же.

Излучения, различные по спектральному составу, ио тождественные по цвету,

называются метамерными.

6.7. Цвет как вектор.

Для определения цвета необходимо указать три величины, например его координаты r′,

g′ и b′. Три оси координат R,G и B должны быгь проведены из начала координат под любым

углом друг к другу. Необходимо только, чтобы три оси не лежали в одной плоскости.

Отложив по осям трй координаты r′, g′ и b′, мы определим точку в пространстве. Каждому

цвету будет соответствовать своя точка. Вся совокупность возможных цветов займет

некоторый объем, образуя цветовое тело. Если не поставлены какие-либо условия

нормирования, объем цветового тела не ограничен, поскольку не ограничены значения

координат r′, g′ и b′. Все реально существующие цвета будут размещаться внутри некоторого

конуса с вершиной в начале координат и с неограниченными по длине образующими.

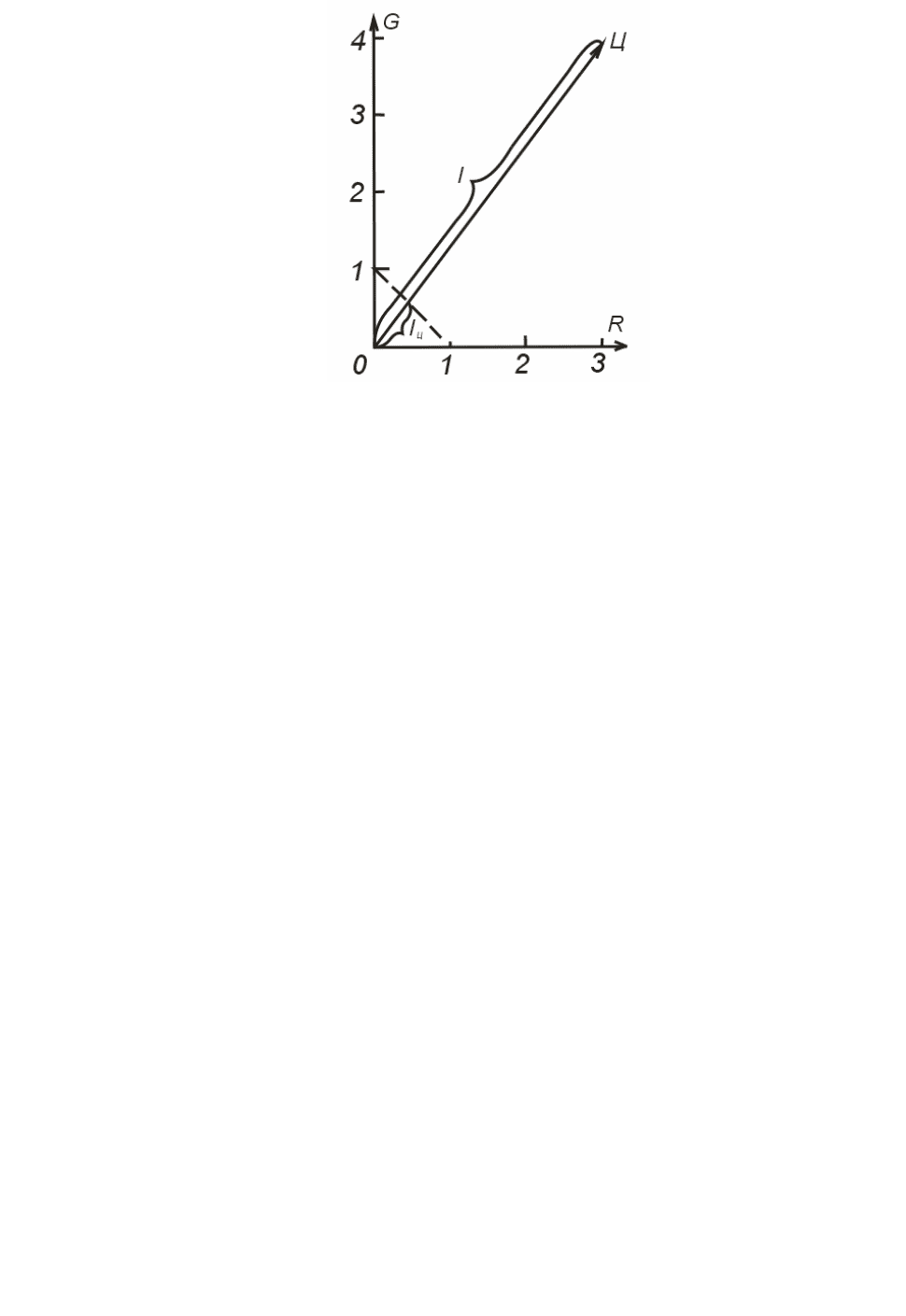
Рис. 6.3. Зависимость единицы цвета от направления его вектора.

Как уже было сказано, оси координат могут располагаться под разными углами, что

принципиально не имеет значения. Примем, однако, что углы между осями прямые, т. е.

будем пользоваться наиболее привычной декартовой прямоугольной системой координат.

Если в точку, изображающую цвет, провести прямую из начала координат, получится вектор.

Представление цвета в виде вектора удобно тем, что цвета можно складывать по правилу

сложения векторов. Однако в колориметрии метрика векторов имеет некоторые особенности.

Как известно, вектор характеризуется направлением и модулем. В обычном векторном

исчислении модуль вектора равен корню квадратному из суммы квадратов его координат. В

колориметрии модуль вектора, изображающего цвет, равен просто сумме его координат. Это

«просто» кажется столь же неожиданным, как утверждение, что гипотенуза равна сумме

катетов. Поэтому попробуем сразу разъяснить суть дела. Покажем на простом примере,

каким образом модуль вектора цвета оказывается равным сумме его координат. Пусть цвет Ц

имеет координаты r′ = 3, g ′= 4, b′ = 0. Равенство нулю одной из координат позволяет нам

изображать цвет Ц на плоскости (рис. 6.3). Все дело в том, что для каждого направления

цветового вектора имеется свой масштаб, своя единица измерения его модуля. Найти

масштаб можно с помощью плоскости, уравнение которой

r′ + g′ + b′ = 1. (6.10)

Отрезок вектора цвета от начала координат до точки пересечения его вектором

плоскости (6.10) равен единице измерения модуля этого вектора. На рисунке след плоскости

{6.10) изображен штриховой линией и отрезок l

дает единицу измерения цвета Ц. Согласно

правилу определения модуля вектора цвета, модуль l найдем сложением:

L = r′ + g′ = 3 + 4 = 7.

Взяв в руки измерительную линейку, мы убедимся, что l/l

= 7.

6.8. Законы Грасмана.

После работ Томаса Юнга цвет привлек внимание таких ученых, как Герман

Гельмгольц (1821–1894), математик Герман Грасман (1809–1877), физик Эрвин Шрёдингер

(1887–1961). Они помогли выработать подлинно научный подход к изучению цвета и

методам его измерения. Математические основы цветовых измерений сформулированы

Грасманом. Три его закона, многократно подтвержденные экспериментом, могут быть

сопоставлены с общими законами математики. Вот как можно сформулировать законы

Грасмана:

1. Глаз может регистрировать только три вида различий в цвете, выражаемые,

например, в различении цветового тона, чистоты цвета и яркости.

2. Если в смеси трех цветовых стимулов один меняется непрерывно, в то время как два

других остаются постоянными, цвет смеси также изменяется непрерывно.

3. Результат смешения двух (или большего числа) стимулов зависит только от цветов

этих стимулов и не зависит от того, какой спектральный состав излучения обуславливал цвет

каждого из стимулов.

Из третьего закона вытекает ряд важных следствий:

а. Пусть имеются две пары цветов: Ц

, Ц

и Ц

, Ц

, причем Ц

= Ц

и Цз = Ц

. Если

образовать из них две смеси, то Ц

+ Ц

= Ц

+ Ц

б. Такое же равенство сохранится и при вычитании цветов: Ц

– Ц

= Ц

– Ц

в. Если цвет Ц

равен Ц

, то повышение интенсивности обоих цветов или понижение ее

в одинаковое число раз не нарушит равенства, т. е. если Ц

= Ц

, то и аЦ

= аЦ

, где а –

любое число, которое может быть как больше, так и меньше единицы.

Следствия из третьего закона Грасмана можно назвать законами линейности при

установлении цветовых равенств. Следствия «а» и «б» показывают, что при уравнивании

цветов сохраняется аддитивность, а следствие «в» указывает на сохранение

пропорциональности. Здесь следует напомнить о существовании метамерных цветов.

Данный цвет может быть обусловлен бесчисленным разнообразием набора излучений самого

различного спектрального состава. Но уж раз любой из этих составов обусловил этот цвет,

нам (так и хочется сказать, ему) уже нет дела до его спектрального состава. Как

определенный цвет он проявляет себя всегда одинаково.

6.9. Цвет – физическая величина.

В повседневной речи слово «цвет» характеризует обычно некоторое ощущение. В

колориметрии цвет – строго определенная величина. В Международном светотехническом

словаре (39) эти два понимания слова разграничиваются таким образом:

1. Цвет (воспринимаемый); цветовое ощущение – аспект зрительного восприятия,

позволяющего наблюдателю различать цветовые стимулы, отличающиеся по спектральному

составу излучения, т. е. отличать один объект от другого, если различие между ними

обусловлено только различием спектрального состава исходящего от них света.

2. Цвет (в колориметрии) – трехмерная векторная величина, характеризующая группу

излучений, визуально неразличимых в колориметрических условиях наблюдения, т. е. в

таких условиях визуального сравнения, при которых любые излучения одинакового

спектрального состава неразличимы глазом.

В словаре во избежание путаницы рекомендуется после слова «цвет» указывать, что

имеется в виду – ощущение или колориметрическая величина, и вместе с тем оговаривается,

что пояснений можно не делать, если смысл ясен из контекста. В нашей книге слово «цвет»

всюду означает колориметрическую величину, а когда речь пойдет об ощущениях, это будет

прямо указываться. Здесь, однако, могут возникнуть сомнения. Можно ли разграничить эти

два смысла слова? Ведь не было бы глаза, не было бы цветового зрения, нельзя было бы и

говорить о ка-ком-либо цвете да еще называть его физической величиной. Но проведем

аналогию. Световой поток, освещенность, яркость – все это, несомненно, физические

величины, широко практически используемые в светотехнике. Непрерывно

совершенствуются источники света, и показателем качества лампы служит прежде всего ее

световая отдача: сколько люменов дает она на ватт расходуемой мощности.

Если возникает сомнение в том, что рабочие места в каком-нибудь цехе достаточно

освещены, что происходит дальше? Быть может, приходит комиссия и один говорит: «Да,

темновато», а другой: «А мне сдается, что света достаточно»? Конечно, вопрос решается

иначе. Приходит контролер и объективным люксметром измеряет: 500 люкс. А по

официально утвержденным нормам для данного вида работ требуется 750 люкс.

Составляется акт, кого-то обязывают увеличить освещенность, а быть может, и наказывают

за несоблюдение норм.

Впрочем, физическая сущность световых величин уже доказана в § 3.5. Совершенно

аналогичным образом и цвет следует считать объективной физической величиной, вполне

определенные значения трех координат которой могут быть найдены по той же спектральной

плотности мощности P

и таблице координат сложения для стандартного

колориметрического наблюдателя МКО (см. табл. 6.1). По формулам (6.9) цвет может быть

вычислен или измерен совершенно независимо от каких-либо визуальных наблюдений, а

следовательно, на полученную величину не повлияют ни индивидуальные особенности

наблюдателя, ни состояние адаптации его зрения.

Если завод выпускает какую-либо окрашенную продукцию: ткани, бумагу, пластмассу,

то, как правило, наряду с другими показателями качества продукции оговаривается ее цвет.

И если выпущенная продукция отклоняется от заданного цвета, это отклонение легко может

быть установлено прямыми объективными измерениями. Для ряда продуктов важен не

только их цвет при выпуске, но и сохранение этого цвета при воздействии света, погодных

уоловий и т. п. Поэтому разрабатываются методы испытания стойкости цвета продукции (см.

например, (32)), и к такой стойкости тоже предъявляются определенные требования.

Утверждению, что цвет есть объективная физическая величина, отнюдь не

противоречит тот несомненный факт, что один и тот же цвет может вызывать в разных

условиях весьма различные ощущения. Мы приведем примеры, когда это изменение

ощущения весьма резко. Но это только подчеркивает, что цвет и ощущение цвета – понятия

совершенно разные, их нельзя путать друг с другом.

Ощущению цвета, его восприятию и своеобразной логике этих восприятий мы

посвятим особую главу – 16.

Глава 7. Цветность.

7.1. Единичная плоскость.

Изобразим множество цветов Ц

, Ц

, ..., Ц

в прямоугольной декартовой системе

координат с ортами. R, G, В. Получим множество различных векторов. Некоторые векторы

будут, быть может, иметь одинаковое направление, что будет означать, что они отличаются

только роличественно, по яркости. Рассечем теперь оси единичной плоскостью,

пересекающей всё три оси в их положительных направлениях на; расстоянии единицы от

начала координат, в точках r′ = 1, g′ = b′ = 0; g′ = 1,r′ = b′ = 0; b′ = 1, r′ = g′ = 0

Возьмем один из векторов цвета – цвет Ц

. Он перёсечет единичную плоскость в

некоторой точке A, Отрезок прямой, начйнающийся в начале координат и кончающийся в

точке А, называют единичным вектором, характеризующим направление вектора Ц

Если

координаты цвета Ц

суть r′, g′ и b′, то координаты конца соответствующего единичного

вектора, т. е. координаты цвётности, будут

'''

;

'''

;

'''

bgr

. (7.1)

Координаты единичного вектора обозначаются теми же буквами, что и координаты

цвета, но без штриха. Легко видеть, что сумма координат единичного вектора равна единице:

r + g + b = 1. (7.2)

Видно, что формула (7.2) и есть уравнение единичной плоскости. Модуль единичного

вектора определяет ту единицу, которой измеряют модуль вектора соответствующего

направления, в нашем примере модуль вектора Ц

. Определяет единичный вектор и

направление вектора Ц

, но модуля его не определяет.

Что же это значит физически? Яркость пропорциональна модулю. Значит, единичный

вектор ничего не говорит о яркости цвета. Если обратиться к другой системе, о которой мы

говорили в четвертой главе, единичный вектор характеризует длину волны λ и чистоту цвета

р. По установившейся терминологии единичный вектор определяет цветность.