Луцко А.Н., Марцулевич Н.А. и др. Механика

Подождите немного. Документ загружается.

101

стержня будет испытывать деформацию растяжения, в результате

чего стержень удлинится. Пусть длина стержня после нагружения

равна

. Тогда разность ΔL = L

– L представляет собой абсолютное

удлинение стержня, а отношение ε =

ΔL/L характеризует

относительное удлинение стержня. Поскольку продольная сила во

всех поперечных сечениях одинакова, деформация также не будет

зависеть от продольной координаты. Поэтому величина ε в данном

случае будет равна относительной продольной деформации

материала стержня, определяемой первым равенством (5.1).

Эксперименты показывают, что материал стержня в условиях его

растяжения будет испытывать не только продольную, но и

поперечную деформацию. Если

h – характерный поперечный размер

стержня до нагружения, то после приложения растягивающей силы

он уменьшится и станет равным h

. Величина ε* = (h

– h)/ h = Δ h/ h

характеризует относительную поперечную деформацию стержня.

Оказывается, что относительные продольная и поперечная

деформации связаны между собой. Их отношение для каждого

конструкционного материала есть величина постоянная, не зависящая

от характера нагружения, которому подвергается элемент

оборудования. Таким образом, отношение деформаций в двух

взаимно перпендикулярных направлениях является индивидуальной

характеристикой материала. Она называется

коэффициентом

Пуассона







(5.7)

Знак абсолютной величины отражает тот факт, что величины ε и ε*

имеют разные знаки. При растяжении продольная деформация

положительна, а поперечная отрицательна. При сжатии продольная

деформация меньше нуля, а поперечная положительная: поперечный

размер после нагружения сжимающей силой увеличивается.

Обратимся теперь к напряжениям, возникающим при растяжении

стержня. Они связаны с продольной силой соотношением (5.4). Но

продольная сила по величине равна силе

F. Поэтому между

напряжениями в материале и силой, приложенной к стержню, имеет

место следующая зависимость:







Поскольку сила действует строго по оси стержня, напряжения во всех

точках поперечного сечения одинаковы. Следовательно, величину



можно вынести из под знака интегрирования. Оставшийся интеграл

102

равен площади поперечного сечения А. Поэтому для определения

напряжений при растяжении (сжатии) получаем простую формулу:





(5.8)

Ранее уже отмечалось, что появление в материале внутренних сил

(а значит, и напряжений) есть результат реакции элемента

оборудования на внешние нагрузки и вызываемые ими деформации.

Другими словами, напряжения в материале являются следствием его

деформации. Поэтому эти величины должны быть количественно

связаны между собой. Действительно, между напряжениями и

деформациями в области упругого изменения размеров и формы

твердых тел имеет место линейная зависимость:



= Е ε . (5.9)

Это соотношение называется законом Гука при растяжении (сжатии).

Закон Гука устанавливает прямую пропорциональность между

величинами





. Коэффициент пропорциональности Е называется

модулем продольной упругости или модулем Юнга. Он

представляет собой важнейшую механическую характеристику

конструкционных материалов и является величиной справочной.

Поскольку относительная деформация

– величина безразмерная,

модуль продольной упругости имеет размерность напряжения, т. е. Па

= Н / м

. Следовательно, по своему физическому содержанию модуль

Е является некоторым напряжением. Из равенства (5.9) ясно, что это

напряжение, при котором

 = 1. Но относительная продольная

деформация становится равной единице тогда, когда длина стержня

при растяжении удваивается. Таким образом, величина модуля

продольной упругости характеризует напряжения, которые возникли

бы в материале, если бы его длина при растяжении увеличилась в два

раза. Поэтому для основных конструкционных материалов модуль

достигает очень больших значений. Например, для сталей Е ≈

210

Па. Конечно, задолго до того, как будут достигнуты напряжения

такой величины, элемент конструкции разрушится.

От величины модуля продольной упругости зависит также

склонность материала к деформированию под действием заданных

нагрузок. Из (5.9) следует, что при фиксированной картине

напряжений величина относительной деформации уменьшается с

увеличением

Е.

Выразим в (5.9) напряжения через растягивающую силу с помощью

(5.8), а относительную деформацию через абсолютное удлинение:

103





или



(5.10)

Полученное равенство называют законом Гука в абсолютных

удлинениях

. Оно позволяет при заданной геометрии стержня, модуле

продольной упругости и растягивающей силе рассчитать величину

удлинения стержня. Произведение

АЕ, стоящее в знаменателе,

называется

жесткостью стержня при растяжении. Оно совокупным

образом отражает влияние механических свойств материала и

геометрии поперечного сечения на величину перемещений.

Соотношения (5.8) и (5.10) позволяют реализовать расчеты на

прочность и жесткость при растяжении (сжатии). Пусть известна

величина допускаемых напряжений [

] для данного конструкционного

материала. Тогда

условие прочности будет состоять в естественном

требовании, чтобы максимальные напряжения, возникающие в

материале стержня, не превосходили допускаемых значений:

][

max





(5.11)

Здесь использовано соотношение (5.8) для нормальных напряжений,

а знак абсолютной величины учитывает тот факт, что при сжатии

продольная сила отрицательна.

Несмотря на простой вид, условие прочности (5.11) используется

при всех видах инженерных расчетов. При проектном расчете

неравенство решается относительно площади поперечного сечения

А,

что позволяет установить минимальное значение поперечных

размеров стержня, при которых условие прочности выполняется.

При поверочном расчете, когда известны фактические размеры

элемента оборудования и действующие на него силы, проверяется

справедливость неравенства (5.11). Наконец, при нагрузочном

расчете неравенство решается относительно максимальной величины

продольных усилий и определяется предельное значение

растягивающей силы, при котором условие прочности будет все еще

выполнено.

Аналогичные расчеты могут быть реализованы с помощью

соотношения (5.10), когда известно допускаемое значение

относительного удлинения стержня [Δ

L/L]. Тогда условие жесткости

будет состоять в требовании, чтобы максимальное удлинение

стержня, приходящееся на единицу его длины, не превышало

допускаемого значения:

104



















max

(5.12)

Это неравенство также используется при всех видах инженерных

расчетов по критерию жесткости.

В заключение этого подраздела рассмотрим важный вопрос о том,

как зависит величина напряжений от ориентации сечения. В

подразделе 5.3 уже отмечалось существование такой зависимости. На

рис. 33 показано сечение стержня, составляющее угол

α с поперечным

сечением. Площади поперечного

А и наклонного А

сечений связаны

простым соотношением:

А = А

cos α. В каждой точке наклонного

сечения действует внутреннее напряжение

р, вектор которого

параллелен оси стержня. Действие напряжения

р по всей площади А

количественно характеризуется продольной силой N. Поэтому

справедливо равенство:

р А

= N. С другой стороны, согласно (5.8),

имеем:

N = р А. Следовательно, величина внутреннего напряжения

меняется в зависимости от угла наклона сечения по закону:

р =



cosα

( - величина напряжения в поперечном сечении). Разложим теперь

вектор

р на нормальное и касательное напряжения (рис. 33). В

результате получим следующие зависимости:



=р cos α =



cos

α,



= p sin α = p sin α cos α =



2sin

(5.13)

Несложный анализ этих соотношений приводит к следующим

выводам. Когда сечение стержня перпендикулярно его оси (

α = 0),

нормальное напряжение равно



, касательное напряжение

отсутствует. В продольных сечениях стержня (

α = π/2) оба напряжения

обращаются в нуль. Следовательно, при растяжении силовое

взаимодействие между продольными слоями материала отсутствует.

Наконец, при

α = π/4 касательные напряжения достигают своего

максимального значения, равного

 / 2.

Рисунок 33

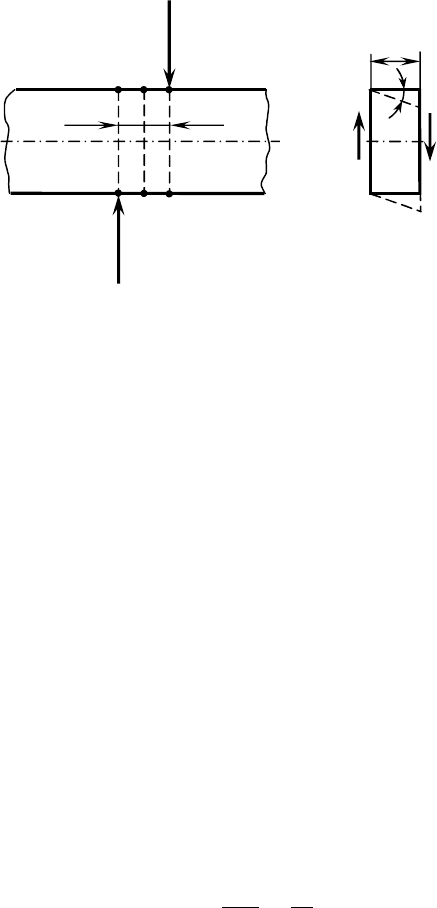
105

5.6. Напряжения и деформации при сдвиге и кручении

Сдвиг и кручение

– два других простых вида нагружения и

деформации, при которых в поперечных сечениях стержня отличен от

нуля только один внутренний силовой фактор. При сдвиге это одна из

поперечных сил, а при кручении

– крутящий момент. В обоих случаях,

согласно формулам (5.5) и (5.6), в сечениях действуют только

касательные напряжения.

Рассмотрим сначала картину силового нагружения стержня,

приводящую к сдвигу (рис. 34). Пусть две равные, но противоположно

направленные силы действуют в поперечных сечениях стержня

ad и

bc, расстояние между которыми h достаточно мало. Такая картина

нагружения возникает, например, при операции резания

металлических листов или прутьев. Если увеличивать силу

F, то

прямые углы элементарного параллелепипеда

abcd сначала

перекашиваются, а затем происходит срез стержня по некоторому

среднему сечению

fe. Таким образом, деформация при сдвиге состоит

во взаимном смещении близлежащих поперечных сечений

относительно друг друга. Величина деформации характеризуется

углом сдвига

γ, который, согласно (5.2), равен отношению

абсолютного сдвига bb′ к расстоянию h между сечениями действия

внешних сил. Из (5.5) следует, что если касательные напряжения



равномерно распределены в сечении стержня, то их величина равна:





(5.14)

Так же как при растяжении (сжатии), напряжения и деформации при

сдвиге связаны между собой линейной зависимостью:



= G



, (5.15)

Рисунок 34

a b

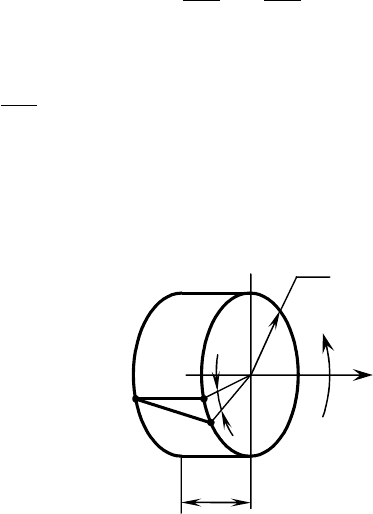
106

которую называют законом Гука при сдвиге. Коэффициент

пропорциональности

G является еще одной механической

характеристикой конструкционных материалов (наряду с модулем

продольной упругости

Е и коэффициентом Пуассона



). Он

называется модулем сдвига. Его значения для различных материалов

содержатся в справочной литературе. Размерность модуля сдвига

–

Па = Н / м

. По физическому смыслу он представляет собой

напряжение, которое возникло бы в материале, если бы угол сдвига

стал равным 1 радиану (это следует из формулы (5.15)). Для сталей

значения модуля

G достигают величин  0.8  10

Па.

При кручении перемещения обусловлены поворотом сечений

стержня вокруг его оси на некоторый угол. На рис. 35 показан элемент

стержня, ограниченный двумя поперечными сечениями с расстоянием

между ними

dx и цилиндрической поверхностью радиуса r. За счет

действия внешнего скручивающего момента сечение 2 повернется

относительно сечения 1 на некоторый угол

d. Это перемещение

можно рассматривать как сдвиг сечения 2 на величину

bb΄

(абсолютный сдвиг) и углом сдвига γ. Длину дуги bb΄ можно выразить

как через угол поворота d, так и через угол сдвига:

bb΄ = r dφ = γ dx.

Здесь величина тангенса угла сдвига заменена его аргументом в силу

малости последнего. Отсюда можно выразить угол сдвига:





 r





Величина





называется относительным углом закручивания.

Она характеризует угол поворота сечений стержня, приходящийся на

единицу его длины.

Рисунок 35

107

Правую часть последнего равенства подставим в закон Гука (5.15).

Получим соотношение, связывающее напряжения в материале при

кручении с величиной перемещений:



= r G Ф (5.16)

Однако использовать это соотношение при расчетах невозможно,

поскольку не известна связь напряжений и перемещений с величиной

крутящего момента. Установим ее. Для этого рассмотрим

элементарную площадку

dA в сечении. Элементарная сила,

обусловленная действием касательных напряжений в пределах

площадки

dA равна:  dA. Как известно из раздела «Статика», момент

этой силы относительно центра сечения

О может быть получен как

произведение величины силы на плечо:

r  dA. С учетом соотношения

(5.16) элементарный момент касательных напряжений, действующих

на площадке dA , определяется выражением: r

G Ф dA. Величина

полного момента касательных напряжений относительно центра

может быть получена путем интегрирования этого выражения по

всему сечению. С другой стороны, согласно (5.6), интегральное

действие напряжений в сечении характеризуется величиной

соответствующего внутреннего силового фактора. В данном случае

это крутящий момент

Т. Следовательно, справедливо равенство:

 



A A

dArGdAGrT

(5.17)

Модуль сдвига и относительный угол закручивания вынесены из под

знака интеграла, поскольку они не зависят от положения точки в

сечении. Интеграл





dArI

(5.18)

аналогичен интегралам (4.23) – (4.25), рассмотренным в разделе

«Динамика». Он носит название полярного момента инерции

поперечного сечения стержня и является его геометрической

характеристикой. Используя обозначение (5.18), из равенства (5.17)

получим следующую формулу для расчета относительного угла

закручивания:





(5.19)

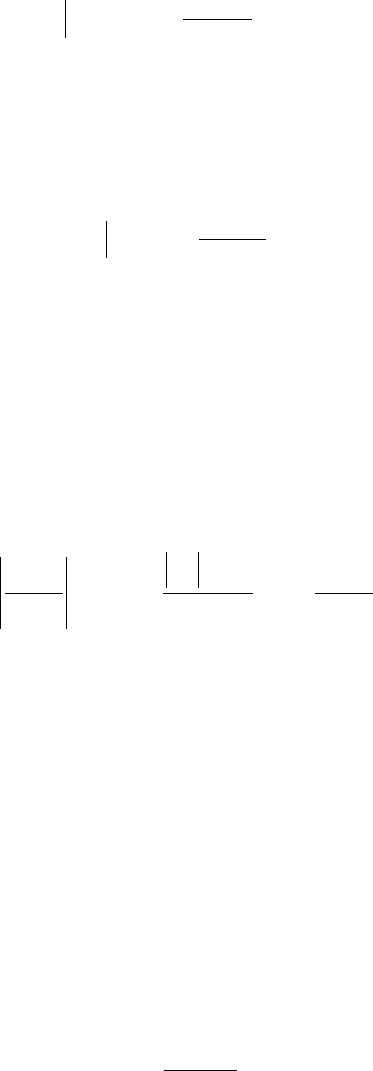
108

Полученное соотношение позволяет количественно оценить

перемещения при кручении, если известна зависимость

действующего в сечениях крутящего момента от продольной

координаты. В самом деле, интегрируя последнее равенство по

участку стержня длиной

L, получим угол, на который повернется одно

крайнее сечение этого участка относительно другого:







(5.20)

Если крутящий момент и сечение стержня не меняются по его длине,

то эта формула упрощается:





(5.21)

Произведение, стоящее в знаменателе, называется жесткостью

стержня при кручении.

Полученные для углов поворота формулы позволяют

сформулировать

условие жесткости при кручении. Так же как и

условие жесткости при растяжении (5.12), оно состоит в естественном

требовании, чтобы максимальные перемещения не превышали

допускаемых значений:



















LGI



max

(5.22)

Слева в этом неравенстве стоит угол поворота сечений стержня,

приходящийся на единицу его длины. Он максимален там, где

действует максимальный по абсолютной величине крутящий момент.

В правой части неравенства участвует допускаемое значение этой

величины, которое для различных элементов оборудования (роторы

центрифуг и сепараторов, валы перемешивающих устройств и т. п.)

могут меняться в пределах (0.5

– 3.5) · 10

-2

рад / м.

Теперь выведем расчетную формулу для определения напряжений

при кручении. Для этого в соотношение (5.16) для касательных

напряжений подставим правую часть формулы (5.19). В результате

получим:





(5.23)

109

Из полученной формулы видно, что величина касательных

напряжений не одинакова в различных точках сечения. В центре

сечения при

r = 0 напряжения в материале отсутствуют. По мере

удаления от центра напряжения увеличиваются пропорционально

расстоянию до него, достигая своих максимальных значений на

периферии сечения. Таким образом, наибольшее значение

напряжения в данном поперечном сечении равно

max

T / I

. Величину

= I

/ r

max

называют полярным моментом сопротивления

поперечного сечения (его размерность м

). Она объединяет все

геометрические характеристики сечения, влияющие на величину

напряжений.

При эксплуатации элементов оборудования, работающих на

кручение, величина максимальных касательных напряжений не

должна превышать допускаемых значений [

]. В этом состоит условие

прочности при кручении

. В символьной форме оно примет вид:

][

max





(5.24)

Допускаемое значение касательного напряжения [] для различных

конструкционных материалов

– величина справочная. Для

большинства материалов оно примерно равно половине допускаемого

нормального напряжения.

5.7. Напряжения, деформации и перемещения при поперечном изгибе

Рассмотрим два оставшихся простых видов нагружения

– чистый

изгиб и плоский поперечный изгиб. В случае чистого изгиба

единственным отличным от нуля внутренним силовым фактором в

поперечном сечении стержня является один из изгибающих моментов.

Стержень, работающий на изгиб, принято называть балкой. На рис.

36 показан элемент стержня, испытывающий чистый изгиб. Под

действием изгибающих моментов ось балки приобретает кривизну,

которая количественно характеризуется локальным значением

радиуса кривизны

. Нетрудно видеть, что на выпуклой стороне

балки материал испытывает удлинение, тогда как на вогнутой

–

сжатие. Следовательно, в центре балки находится слой материала,

который не подвергается ни сжатию, ни удлинению. Этот слой

называется

нейтральным слоем.

Как известно из математики, радиусом кривизны плоской кривой называется

радиус круга кривизны (или соприкасающейся окружности). Величина, обратная

радиусу кривизны, носит название кривизны плоской кривой.

110

Оценим величину деформаций при изгибе. Для этого рассмотрим

отрезок С

D, параллельный оси балки и лежащий на расстоянии у от

нейтрального слоя. До нагружения изгибающим моментом длина

отрезка С

D равнялась длине отрезка АВ на оси балки, которую можно

выразить через радиус кривизны оси балки

r и угол d



: СD = АВ = r





. После нагружения длина отрезка СD стала равной (r + у) d



Следовательно, относительное удлинение отрезка СD оценивается

величиной:

rddyr













)(



(5.25)

Отсюда видно, что величина деформации при изгибе увеличивается с

расстоянием до нейтрального слоя, меняет знак при переходе через

слой и пропорциональна кривизне изогнутой оси балки.

Полученное выражение для относительной деформации подставим

в закон Гука (5.9). Получим следующую связь напряжений с кривизной

оси стержня:

EEy





)(

(5.26)

Воспользоваться полученными формулами для расчета

деформаций и напряжений нельзя, поскольку не известна

зависимость кривизны

1/r от величины изгибающего момента.

Получим ее. Для этого рассмотрим поперечное сечение балки и

действующие в нем напряжения. Выделим малую площадку

dA в

Рисунок 36

Нейтральный

слой

dθ

Δdx