Луцко А.Н., Марцулевич Н.А. и др. Механика

Подождите немного. Документ загружается.

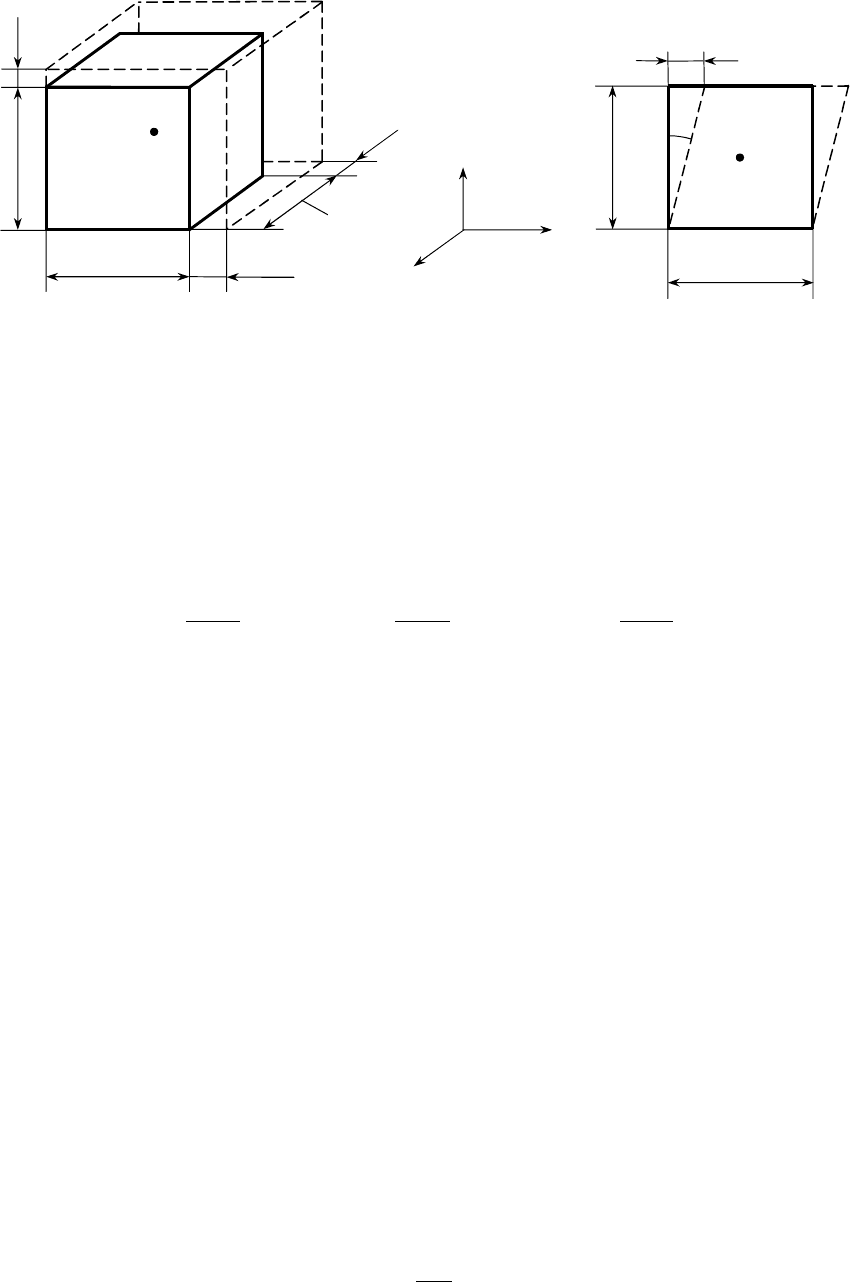
выделим вокруг точки М бесконечно малый параллелепипед со

сторонами

dx, dy, dz (рис. 30). В результате изменения размера и

формы нагруженного тела ребра параллелепипеда получат

удлинения Δ

x, Δy, Δz. Относительными линейными деформациями

в данной точке материала называются величины, определяемые

следующими отношениями:



















(5.1)

В каждом отношении в числителе стоит абсолютное удлинение

элементарного параллелепипеда в данном направлении, а в

знаменателе

– исходная длина параллелепипеда в этом же

направлении до нагружения. Следует заметить, во

-первых, что

относительная линейная деформация (или просто

деформация) –

характеристика сугубо локальная, т. е. она является функцией

пространственных координат. Во

-вторых, в одной точке, но в разных

направлениях она может быть различной.

Относительная деформация размерности не имеет и для обычных

конструкционных материалов это величина порядка 10

-3

. Другими

словами, изменение размеров и формы нагруженных тел, как

правило, незначительны и могут быть измерены лишь специальными

приборами

– тензометрами.

Кроме линейных деформаций в твердом теле возникают угловые

деформации

. Количественно они характеризуются углом сдвига 

(рис. 30), который рассчитывается по формуле:

xyxy









. (5.2)

Рисунок 30

Δdy

Δdx

Δdz

а б

Величина  называется абсолютным сдвигом, а угол



ху

–

относительным сдвигом. Он характеризует перекос элементарного

параллелепипеда в плоскости

ху. Аналогично определяются угловые

деформации в плоскостях

xz и yz, которые обозначаются

соответственно через



хz



уz

. Как и линейные деформации, углы

сдвига также малы. Их значения лежат в области 10

-4

. Поэтому в

формуле (5.2) значение тангенса и его аргумента практически не

отличаются.

Совокупность трех линейных



, 

и трех угловых деформаций



ху



хz



уz

по различным направлениям и плоскостям для данной

точки полностью характеризует

деформированное состояние

конструкционного материала в точке. При известных характеристиках

деформированного состояния во всем объеме материала может быть

оценена величина

максимальных перемещений нагруженной

детали, которые затем сравниваются с их

допускаемыми

значениями. Последние обычно известны из практики эксплуатации

соответствующего оборудования. Количественная оценка и сравнение

максимальных перемещений с допускаемыми значениями составляют

существо

расчетов на жесткость.

С понятием деформаций связано одно из наиболее важных

свойств конструкционных материалов

– их упругость. Под

упругостью, как известно, понимают способность твердых тел

полностью восстанавливать свою форму и размеры после снятия

внешних нагрузок. Точные измерения показывают, что любые

материалы даже при небольших нагрузках получают остаточные

деформации. Так что свойство упругости представляет собой, строго

говоря, еще одну идеализацию из числа тех, на которых строятся

расчетные схемы механики.

При небольших нагрузках величина остаточных деформаций

пренебрежимо мала, но с увеличением нагрузок растут и остаточные

деформации. Для каждого элемента конструкции и каждой детали

существует некие предельные нагрузки, выше которых остаточные

деформации становятся существенными, т. е. деталь необратимо

меняет свои размеры и форму. При эксплуатации технологического

оборудования таких нагрузок допускать нельзя. Все узлы и детали

должны работать в области упругих деформаций.

5.2. Внутренние силовые факторы в конструкционном материале

Возникновением деформаций не исчерпывается реакция

материала на внешние нагрузки. Изменение размера и формы тела

приводит к изменению среднего расстояния между атомами, от

которого очень сильно зависят силы химических связей. В объеме

конструкционного материала появляются силы, обусловленные

изменением сил межмолекулярного взаимодействия. По величине эти

внутренние силы таковы, что они в точности уравновешивают

внешние воздействия на данный элемент конструкции. С помощью

внутренних сил (или сил упругости) материал сопротивляется

механическим нагрузкам.

С увеличением внешних нагрузок внутренние силы также

возрастают. Но и здесь существует предел, после которого в

материале возникают необратимые изменения, и, в конечном счете,

деталь разрушается. Следовательно, для исключения возможных

аварийных ситуаций необходимо уметь рассчитывать величину

внутренних сил и ограничивать их некоторыми «неразрушающими»

значениями, которые обычно определяются экспериментальными

методами. Количественная оценка внутренних сил, возникающих в

элементах конструкции при заданных внешних нагрузках,

представляет собой важнейшую задачу механики деформируемого

тела. Рассмотрим ее применительно к элементу конструкции,

имеющему расчетную схему стержня (см. подраздел 1.3.).

При использовании этой расчетной схемы внутренние силы

определяются с помощью

метода поперечных сечений. Сущность

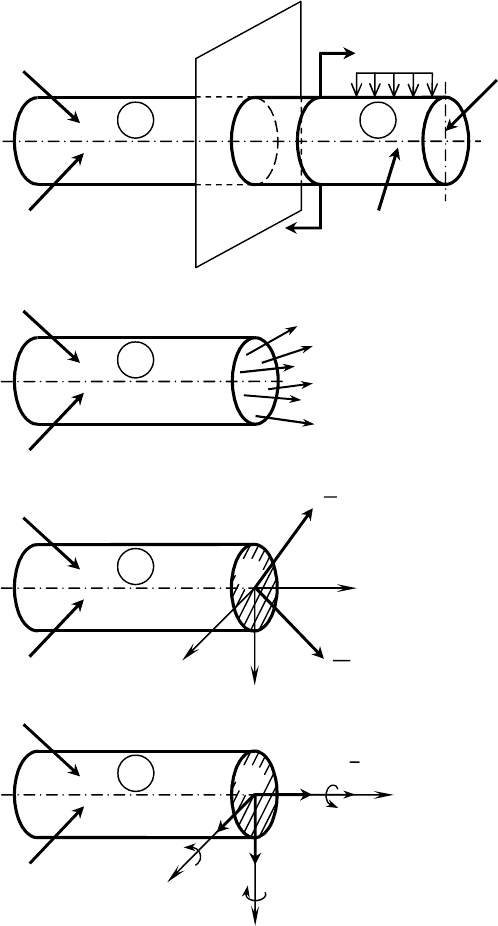
этого метода заключается в следующем. Рассмотрим стержень (рис.

31), находящий в равновесии под действием заданного набора

внешних сосредоточенных сил

, моментов M

и распределенных

нагрузок

(индекс i подразумевает, что нагрузок данного вида может

быть несколько). Мысленно разделим стержень на две части

плоскостью, перпендикулярной его оси (рис. 31, а), и одну из частей

мысленно отбросим. В плоскости, разделяющей обе части стержня,

действуют внутренние силы, отражающие силовое взаимодействие

между частями (рис. 31,б). В соответствии с положениями статики (см.

подраздел 2.5.) всю совокупность внутренних сил, действующих в

сечении, можно привести к главному вектору

R и главному моменту М

с центром приведения в центре тяжести поперечного сечения (рис. 31,

в). Проекции главного вектора и главного момента системы

внутренних сил на оси координат называются

внутренними

силовыми факторами

. В общем случае это шесть скалярных

величин.

Согласно аксиоме 4 статики, силовые факторы в сечениях левой и

правой частей стержня равны по величине и противоположны по

направлению. Чтобы знак силового фактора, определенного для

правой и левой частей стержня, был одинаков, в сечениях вводятся

две системы координат. Ось

Ох направляется вдоль внешней

нормали к сечению, а оси

Оу и Оz располагаются в плоскости

сечения, образуя левую тройку для левой части стержня и правую

–

для правой. На рис. 31,в показано расположение координатных осей

для левой части стержня. Ось

Оу направлена вниз, ось Оz – «на нас».

Для правой части стержня их направление противоположное. В том и

другом случае положительные направления внутренних силовых

факторов совпадают с положительным направлением координатных

осей

Поскольку обе части стержня находятся в равновесии, для каждой

из них справедлива система уравнений (2.17), выражающая условие

равновесия произвольного твердого тела. Система содержит шесть

уравнений, столько же, сколько искомых силовых факторов. Поэтому

их величина и направление действия могут быть определены из

Напомним, что правой тройкой называется система прямоугольных координат, в

которой поворот оси Ох на /2 в направлении, противоположном вращению часовой

стрелки (если смотреть со стороны оси Оz), совмещает полуось положительных х с

полуосью положительных у.

Рисунок 31

решения системы (2.17). Внутренние силовые факторы позволяют

судить о характере воздействия внешних нагрузок на элемент

оборудования. Поэтому рассмотрим их более подробно.

Проекция главного вектора внутренних сил

R на ось Ох называется

продольной силой (рис. 31,г) и обычно обозначается через N.

Продольная сила вызывается деформацией растяжения или сжатия

материала в зависимости от того, направлена она по внешней или

внутренней нормали к сечению стержня. В системе координат,

введенной ранее, сила

N будет иметь знак «+» при растяжении и знак

«-» при сжатии стержня.

Проекции главного вектора внутренних сил на оси

Оу и Оz

называются поперечными силами и обозначаются через Q

и Q

соответственно. Они вызываются деформацией сдвига. Знак

поперечных сил определяется направлением координатных осей в

сечении стержня.

Проекция главного момента внутренних сил М на ось Ох

называется крутящим моментом. Он обозначается через Т и

вызывается деформацией, обусловленной действием пар сил,

которые лежат в плоскости перпендикулярной оси стержня.

Перемещения, возникающие при этом, состоят в повороте сечений

стержня вокруг его оси. Крутящий момент считается положительным,

если он вращает сечение против часовой стрелки, если смотреть со

стороны внешней нормали к сечению, и отрицательным

– в противном

случае.

Проекции главного момента внутренних сил

М на оси Оу и Оz

называются изгибающим моментами и обозначаются

соответственно через

и М

. Изгибающий момент М

препятствует

тем внешним нагрузкам, которые пытаются изогнуть стержень в

плоскости Ох

z, а изгибающий момент М

сопротивляется изгибу

стержня в плоскости Оху (рис. 31,г). Знак изгибающего момента

зависит от того, в какую сторону направлен момент, если смотреть со

стороны положительных значений соответствующей координатной

оси. Если момент направлен против часовой стрелки, он считается

положительным; если по часовой

– отрицательным.

Перечисленные внутренние силовые факторы позволяют ввести

классификацию

простых видов нагружения и деформации

элементов оборудования, имеющих расчетную схему стержня. Если из

всех шести внутренних силовых факторов отлична от нуля только

продольная сила

N, то говорят о растяжении или сжатии в

зависимости от ее знака. Если отлична от нуля только одна из

поперечных сил, то такой вид деформации называется

сдвигом в

направлении соответствующей оси. Когда все силовые факторы

равны нулю, за исключением крутящего момента Т, говорят о

кручении. Если не равен нулю один из изгибающих моментов, то

возникающий вид деформации называется

чистым изгибом в

плоскости действия момента. Наконец, еще одним простым видом

деформации является

плоский поперечный изгиб. К нему относится

такой вид нагружения, при котором одновременно отличны от нуля

изгибающий момент

и поперечная сила Q

либо изгибающий

момент

и поперечная сила Q

. В первом случае оба силовых

фактора препятствуют изгибу стержня в плоскости Оху, а во втором

–

в плоскости Охz.

Все другие случаи сочетания внутренних силовых факторов

свидетельствуют о

сложном нагружении. Большинство элементов

оборудования испытывает именно сложное нагружение. Однако, его

можно рассматривать как результат наложения простых видов

нагружения. Поэтому в механике деформируемого тела в первую

очередь подробно рассматриваются перечисленные выше простые

виды нагружения.

5.3. Напряжения в сечениях стержней

Внутренние силовые факторы в сечениях стержня характеризуют

суммарное действие внутренних усилий в этих сечениях, т. е.

являются их равнодействующими. В общем случае нагружения

распределение внутренних усилий по сечению неравномерно. Очень

часто важно знать, как распределены внутренние усилия по сечению.

Поэтому требуется некая количественная характеристика локальной

величины сил, действующих в объеме конструкционного материала.

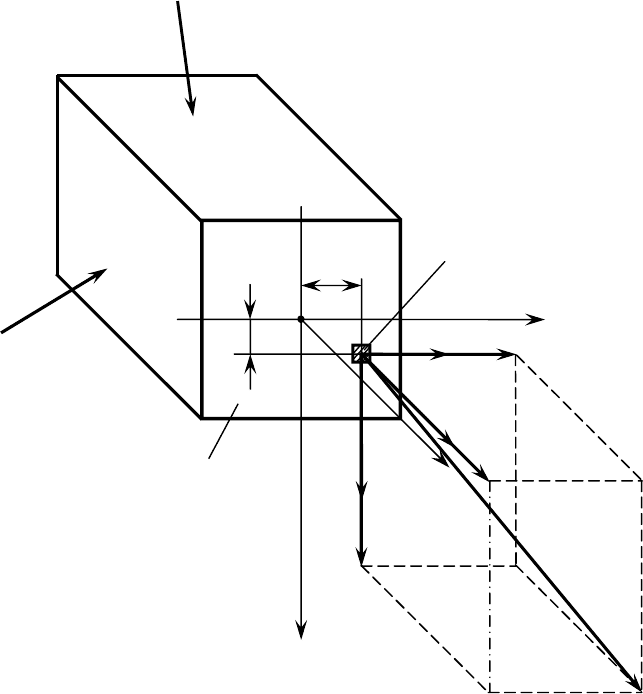
Рассмотрим в сечении стержня произвольную точку

М и выделим в

окрестности этой точки элементарную площадку

dA (рис. 32). Пусть Р

– равнодействующая всех внутренних сил, действующих на площадке

dA. Составим отношение Р / dA. Предел этого отношения, когда

площадка

dA стягивается к точке М, называется вектором полного

внутреннего напряжения

р в данной точке материала. В символьном

виде это определение запишется следующим образом:

lim





(5.3)

Вектор полного напряжения характеризует интенсивность внутренних

усилий, действующих в данной точке материала. Он зависит, как

потом выяснится, не только от положения точки

М, но и от ориентации

площадки

dA в пространстве. Единицей измерения напряжения

является паскаль: Па = Н / м

Проекция вектора полного внутреннего напряжения на

направление нормали к площадке

dA называется нормальным

напряжением

и обозначается через . Его проекция, лежащая в

плоскости сечения, называется касательным напряжением и

обозначается через

 (рис. 32). Характер действия на материал

указанных напряжений различен. Нормальные напряжения стремятся

сблизить или удалить отдельные слои материала друг от друга.

Касательные же напряжения способствуют сдвигу одних слоев

относительно других. Поэтому касательные напряжения называют

еще

напряжениями сдвига. Большинство конструкционных

материалов существенно хуже сопротивляется действию касательных

напряжений, чем нормальных.

Между напряжениями и внутренними силовыми факторами,

действующими в сечении стержня, существует несложная связь. В

самом деле, величина продольной силы

N, например, отражает

совокупное действие нормальных напряжений

, распределенных по

всему сечению. Поэтому они связаны соотношением:







(5.4)

Аналогичные соотношения имеют место для других внутренних

усилий:

Рисунок 32













(5.5)

Более сложная связь между составляющими главного момента

внутренних сил и напряжениями в сечении стержня:





dAzy )(



(5.6)





dAz







dAy



С увеличением внешних нагрузок напряжения в материале деталей

увеличиваются. Так же как и в случае деформаций, напряжения не

могут неограниченно возрастать. Для каждого конструкционного

материала существуют некие предельные напряжения, после которых

в материале начинаются необратимые изменения. Способности

элементов конструкции сопротивляться внешним воздействиям не

беспредельны. Следовательно, для того чтобы по возможности

исключить отказы, связанные с потерей прочности оборудования,

необходимо уметь рассчитывать величину напряжений в материале

при заданных нагрузках. Это позволит установить наиболее опасные

сечения деталей, где напряжения максимальны, и сравнить их с

допускаемыми напряжениями для данного конструкционного

материала. Расчеты такого рода называются

расчетами на

прочность

5.4. Главные критерии работоспособности элементов

технологического оборудования

Расчеты на прочность и жесткость исходят из условия, чтобы

максимальные напряжения и перемещения не превосходили

некоторых предельных значений. Такие условия, по существу,

представляют собой критерии отказа оборудования из

-за потери

прочности и недостаточной жесткости конструкции. Любой вид

технологического оборудования проверяется на выполнение этих

критериев как на стадии проектирования, так и во время эксплуатации.

В силу всеобщности указанных критериев их называют

главными

критериями работоспособности

. Однако прочность и жесткость

далеко не исчерпывают весь набор требований (критериев), которым

должно удовлетворять химическое оборудование. Перечислим и

дадим определения важнейшим из главных критериев

работоспособности.

Под прочностью понимают способность конструкции в целом и

ее отдельных элементов воспринимать, не разрушаясь, действие

внешних нагрузок

Жесткость – способность элемента конструкции получать под

действием внешних нагрузок такие рабочие деформации, которые

не превышают их заданные предельные значения, установленные

на основе опыта проектирования и эксплуатации аналогичных

конструкций

Критерий устойчивости подразумевает способность детали

сохранять под действием внешних нагрузок первоначальную

геометрическую форму

Под виброустойчивостью понимают способность элемента

оборудования работать в нужном эксплуатационном режиме без

недопустимых колебаний (вибраций)

Герметичность – свойство конструкции изолировать ее рабочий

объем так, чтобы утечки рабочих веществ в окружающую среду

были полностью исключены, либо находились в заданных пределах

Существует еще целый ряд менее общих критериев

(теплостойкость, коррозионная стойкость и т. п.), которые также

применяются в химическом машиностроении. Наиболее важным из

них является критерий

износостойкости, т. е. способность

материала данной детали противостоять процессу постепенного

изменения размеров и формы в области ее контакта с

обрабатываемым веществом или другой деталью в результате

трения

Выбор того или иного главного критерия зависит от конкретных

условий эксплуатации и назначения агрегата. Например, элементы

корпуса аппарата, снабженного теплообменной рубашкой, должны

быть рассчитаны с учетом критериев прочности, устойчивости и

герметичности. В то же время элементы ротора перемешивающего

устройства необходимо оценить по критериям прочности, жесткости и

виброустойчивости.

Главные критерии работоспособности лежат в основе всех

инженерных методов расчета химического оборудования. Различают

три вида инженерных расчетов: проектный, поверочный и

нагрузочный. При

проектных расчетах исходными данными являются

характер и величина нагрузок на оборудование, механические

свойства конструкционного материала. В результате расчета

требуется определить размеры элементов конструкции, которые

обеспечат ее работоспособность.

Поверочные расчеты обычно

проводят для существующего оборудования, когда известны размеры

элементов конструкции, характер и величина нагрузок, механические

свойства конструкционного материала. Целью поверочных расчетов

является проверка выполнения всех критериев работоспособности,

определяющих нормальное функционирование данного аппарата или

100

его узла. Наконец, нагрузочные расчеты преследуют цель

нахождения предельных значений внешних нагрузок, при которых

работоспособность оборудования еще не нарушится.

Инженер

-технолог принимает непосредственное участие в

инженерных расчетах всех трех видов. При проектировании нового

оборудования его задачей является составление

технического

задания

, которое служит основанием для последующих стадий

конструкторских работ:

технического предложения, эскизного

проекта

, технического проекта и рабочей конструкторской

документации

. В техническом задании указываются назначение и

рабочие параметры проектируемого агрегата (производительность,

рабочее давление и температура, свойства обрабатываемой среды,

гидродинамические режимы, основные геометрические размеры),

допускаемые безопасные отклонения от рабочих параметров,

требования к конструкционным материалам с точки зрения их

коррозионной стойкости по отношению к обрабатываемой среде и т. д.

На следующих стадиях разработки нового оборудования технолог

обычно контролирует качество конструкторских решений на предмет

их технологичности и соответствия техническому заданию.

Непосредственно проектные расчеты проводит инженер

-конструктор.

Поверочные и нагрузочные расчеты целиком лежат в сфере

ответственности технолога. Первые проводятся с целью контроля

работоспособности существующего оборудования после его

эксплуатации в течение определенного срока. С помощью

нагрузочных расчетов определяют возможный резерв оборудования

по нагрузкам (по рабочему давлению, потребляемой мощности,

частоте оборотов и т д.).

Некоторые примеры всех трех видов инженерных расчетов будут

рассмотрены при анализе простых видов нагружения.

5.5. Напряжения и деформации при растяжении и сжатии стержней

Согласно классификации простых видов деформации при

растяжении или сжатии из шести внутренних силовых факторов

отлична от нуля только продольная сила

N. К расчетной схеме

стержня, испытывающего деформации сжатия или растяжения, могут

быть приведены такие важные конструктивные элементы химического

оборудования, как трубные пучки кожухотрубчатых теплообменников,

опорные стойки емкостных аппаратов, штоки компрессоров и

поршневых насосов, болты и шпильки фланцевых соединений и т. д.

Рассмотрим стержень длины

L, нагруженный растягивающей силой

F, которая действует строго вдоль оси стержня. Тогда, применяя

метод сечений, нетрудно убедиться, что в каждом поперечном

сечении будет действовать продольная сила

N, равная по величине

силе

F и направленная вдоль внешней нормали к сечению. Материал